Номер 365 по математике 5 класс: Номер №365 — ГДЗ по Математике 5 класс: Виленкин Н.Я.

Содержание

Математика ⁠Абылкасымова 5 класс 2017 Упражнение 365 ГДЗ(дүж) решебник KZGDZ.COM

Глава 3. ОБЫКНОВЕННЫЕ ДРОБИ И ДЕЙСТВИЯ НАД НИМИ § 20. Изображение обыкновенных дробен и смешанных чисел на координатном луче Упражнение 365

← Предыдущий Следующий →

Глава 1. НАТУРАЛЬНЫЕ ЧИСЛА И НУЛЬ

§ 1. Запись натуральных чисел

Упражнение

12345678910111213

§ 2. Координатный луч

Упражнение

14151617181920212223242526

§ 3. Сравнение натуральных чисел

Упражнение

2728293031323334353637383940

§ 4. Арифметические действия е натуральными числами

Упражнение

4142434445464748495051525354555657585960

§ 5. Числовые и буквенные выражения. Упрощение выражений

Упражнение

61626364656667686970717273747576777879

§ 6. Уравнения

Упражнение

808182838485868788899091

§ 7. Формулы. Вычисления по формулам

Упражнение

9293949596979899100101102

§ 8.

Решение текстовых задач

Упражнение

103104105106107108109110111112113114115116117118119120121122

§ 9. Последовательность из натуральных чисел

Упражнение

123124125126127128129130131132

Глава 2. ДЕЛИМОСТЬ НАТУРАЛЬНЫХ ЧИСЕЛ

§ 10. Делители и кратные натуральных чисел. Простые и составные числа

Упражнение

133134135136137138139140141142143144145146147148149150151152153

§11. Основные свойства делимости

Упражнение

154155156157158159

160161162163164165166167168169170

§ 12. Признаки делимости на числа 2. 3, 5, 9.

Упражнение

171172173174175176177178179180181182183184185186187188189190191192193194

§13. Степень

Упражнение

195196197198199200201202203204205206207208209210211212

§14. Разложение натурального числа на простые множители

Упражнение

213214215216217218219220221222223224225226227228229230231232233

§15. Наибольший общий делитель (НОД) и наименьшее общее кратное (НОК)

Упражнение

234235236237238239

240241242243244245246247248249250251252253254255256257258259

Глава 3.

ОБЫКНОВЕННЫЕ ДРОБИ И ДЕЙСТВИЯ НАД НИМИ

§ 16. Обыкновенная дробь. Чтение и запись обыкновенных дробей

Упражнение

260261262263264265266267268269270271272273274275276277278279280281282283284285286

§ 17. Основное свойство обыкновенной дроби

Упражнение

287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319

320321322323324325

§ 18. Правильные и неправильные обыкновенные дроби. Смешанные числа

Упражнение

326327328329330331332333334335336337338339340341342343344345

§19. Перевод неправильной обыкновенной дроби в смешанное число и смешанного числа в неправильную обыкновенную дробь

Упражнение

346347348349350351352353354355356357358359360361362363364

§ 20. Изображение обыкновенных дробен и смешанных чисел на координатном луче

Упражнение

365366367368369370371372373374375376377378379380381

§ 21. Приведение обыкновенных дробей к общему знаменателю

Упражнение

382383385386387388389390391392393394395396397398

§ 22.

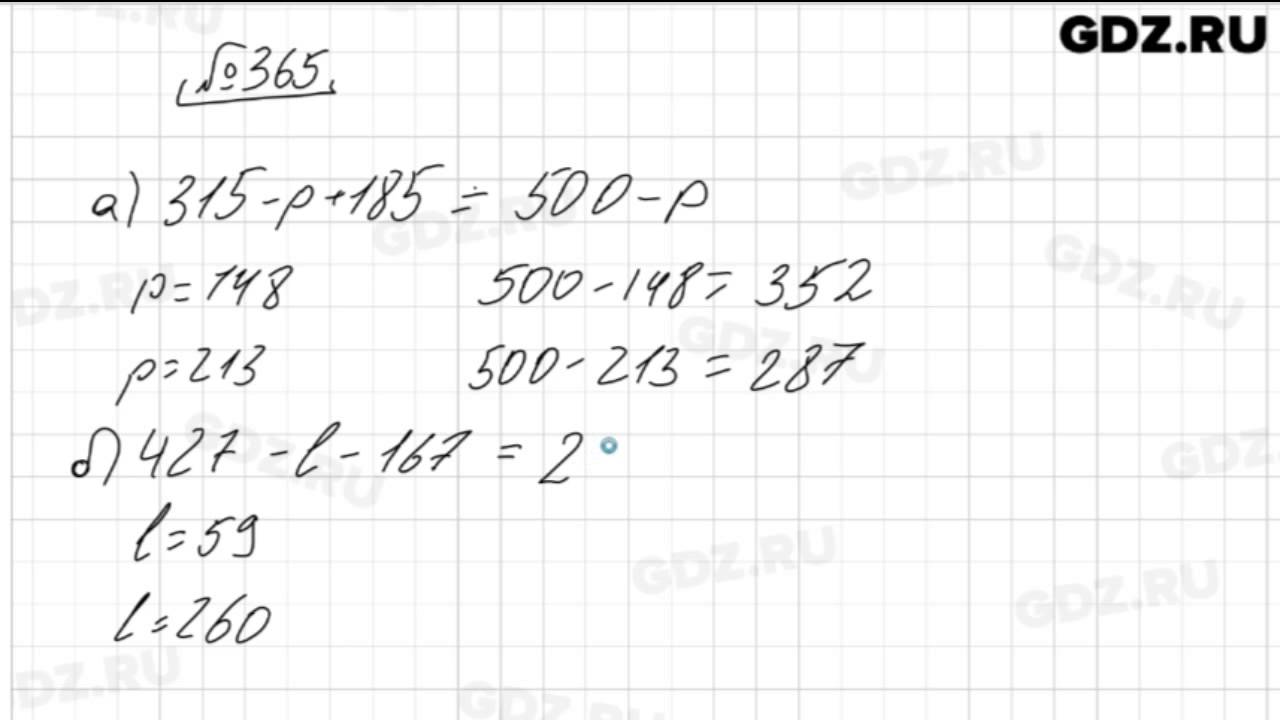Сравнение обыкновенных дробей и смешанных чисел

Упражнение

399400

401402403404405406407408409410411412413414415416417418419420

§ 23. Сложение и вычитание обыкновенных дробей

Упражнение

421422423424425426427428429430431432433434435436437438439440441442443444445446447448449450451452453454

§ 24. Сложение смешанных чисел

Упражнение

455456457458459460461462463464465466467468469470471472473474475476477478

§ 25. Вычитание смешанных чисел

Упражнение

479480

481482483484485486487488489490491492493494495496497498499500501502503

§ 26. Умножение обыкновенных дробей и смешанных чисел

Упражнение

504505506507508509510511512513514515516517518519

§ 27. Деление обыкновенных дробей и смешанных чисел

Упражнение

520521522523524525526527528529530531532533534535536537

§ 28. Действия с обыкновенными дробями, нулем, натуральными и смешанными числами

Упражнение

538539540541542543544545546547548549550551552553554555556

Глава 4.

ТЕКСТОВЫЕ ЗАДАЧИ

§ 29. Нахождение дроби от числа и числа по его дроби

Упражнение

557558559560

561562563564565566567568569570571572573574575576577578

§ 30. Задачи на совместную работу

Упражнение

579580581582583584585586587588589590591592593

Глава 5. ДЕСЯТИЧНЫЕ ДРОБИ II ДЕЙСТВИЯ НАД НИМИ

§ 31. Десятичная дробь. Чтение и запись десятичных дробей

Упражнение

594595596597598599600601602603604606607

§ 32. Перевод десятичной дроби в обыкновенную дробь

Упражнение

608609610611612613614615616617

§ 33. Изображение десятичных дробей на координатном луче. Сравнение десятичных дробей

Упражнение

618619620621622623624625626627628629630631632633

§ 34. Сложение и вычитание десятичных дробей

Упражнение

634635636637638639640641

642643644645646647648649650

§ 35. Умножение десятичной дроби на натуральное число

Упражнение

651652653654655656657658659660661662663664665666667668669

§ 36.

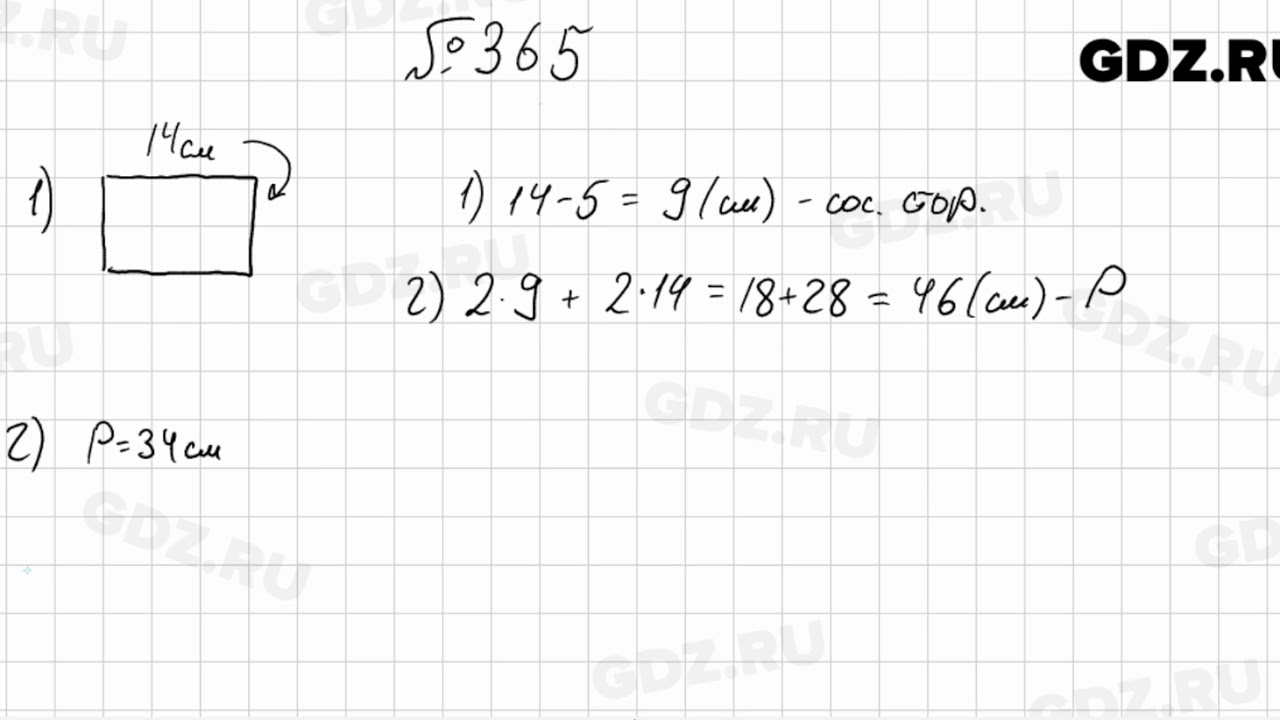Умножение десятичных дробей

Упражнение

670671672673674675676677678679680681682683684685

§ 37. Деление десятичной дроби на натуральное число

Упражнение

686687688689690691692693694695696697698699700701

§ 38. Деление десятичных дробей

Упражнение

702703704705706707708709710711712713714715716717718719720

§ 39. Умножение и деление десятичных дробей на 10. 100. 1000. … и на 0.1. 0,01, 0,001

Упражнение

721

722723724725726727728729730731732733734735736

§ 40. Действия с десятичными и обыкновенными дробями

Упражнение

737738739740741742743744745746747748749750751752753754755756757

§41. Округление чисел

Упражнение

758759760761762763764765

§ 42. Решение текстовых задач

Упражнение

766767768769770771772773774775776777778779

Глава 6. МНОЖЕСТВА

§ 43. Множество. Элементы множества. Изображение множеств

Упражнение

780781782783784785787

§ 44. Отношения между множествами.

Подмножества

Упражнение

788789790791792793794795

§ 45. Объединение и пересечение множеств

Упражнение

796797798799800

§ 46. Решение текстовых задач

Упражнение

801802

803804805806807808

Глава 7. ПРОЦЕНТЫ

§ 47. Процент

Упражнение

809810811812813815816817818819820821822823824825826828829830831

§ 48. Нахождение процентов от числа и числа по его процентам

Упражнение

832833834835836837838839840841842843

§ 49. Решение текстовых задач

Упражнение

844845846847848849850851852853854855856857858859860861862863864865866867868869

Глава 8. УГЛЫ. МНОГОУГОЛЬНИКИ

§ 50. Угол

Упражнение

870871872873874875876877878880881

§ 51. Многоугольники

Упражнение

882883884885

886887888889890

Глава 9. ДИАГРАММЫ

§ 52. Окружность. Крут

Упражнение

891892893894895896897898899901902

§ 53. Диаграмма. Представление статистических данных с помощью диаграмм

Упражнение

903904906907908909910911912913915916917919920921

Глава 10.

РАЗВЕРТКИ ПРОСТРАНСТВЕННЫХ ФИГУР

§ 54. Прямоугольный параллелепипед (куб) и его развертка

Упражнение

922923924926

§ 55. Задачи на разрезание фигур. Задачи на складывание фигур

Упражнение

929930931932933934

Глава 11. УПРАЖНЕНИЯ ДЛЯ ПОВТОРНЕИЯ

Упражнение

937938939940941942943944945946947948949950951952953954955956957958959960961962963964965966967968969970971972973974

975976977978979980

№ 365 ГДЗ Математика 5 класс Дорофеев, Петерсон Часть 2. Помогите мне решить все эти примеры! – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Выполни деление

ответы

Привет.

Их много, но они легкие!

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения

похожие темы

3 класс

Репетитор

Химия

Алгебра

похожие вопросы 5

Координатная прямая. Математика 5 класс.Зубарева И.И.Параграф 10, задание 191

Укажите начало отсчёта и координаты точек А, В, С, (Подробнее…)

ГДЗЗубарева И.И.Математика5 класс

Помогите установить соответствие между неравенствами. Математика базовый уровень ЕГЭ — 2017. Вар.№1. Зад.№17. Под руководством Ященко И.В.

Здравствуйте! Помогите установить соответствие между неравенствами и их решениями: (Подробнее…)

ЕГЭЭкзаменыМатематикаЯщенко И.В.

Помогите выбрать утверждения. Математика базовый уровень ЕГЭ — 2017. Вар.№1. Зад.№18. Под руководством Ященко И.В.

Здравствуйте! Перед волейбольным турниром измерили рост игроков волейбольной команды города N. Оказалось, что рост каждого из (Подробнее.

..)

ЕГЭЭкзаменыМатематикаЯщенко И.В.

Вырежи из бумаги № 694 ГДЗ Математика 6 класс Дорофеев Г.В. Часть3.

Вырежи из бумаги 20 одинаковых произвольных треугольников и составь
из них паркет. Всегда ли это можно сделать? Почему?

ГДЗМатематика6 классДорофеев Г. В.

11. Выпишите слово, в котором на месте пропуска пишется буква Е. Русский язык ЕГЭ-2017 Цыбулько И. П. ГДЗ. Вариант 12.

11.
Выпишите слово, в котором на месте пропуска пишется буква Е.
произнос., шь (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

Суммирование

— Какова формула 365-дневного пенни-челленджа?

спросил 7 лет, 6 месяцев назад

Изменено 5 лет, 2 месяца назад

Просмотрено 125 тысяч раз

$\begingroup$

_{Не совсем дубликат, поскольку это ответ на конкретный случай, популярный в социальных сетях.}

Возможно, вы видели вирусные сообщения о том, что « сэкономьте по пенни в день в течение года и заработайте 667,95 долларов! ». Конечно, задача состоит в том, чтобы добавить в банку несколько копеек за текущий день. Итак:

 День 1 = + .01
День 2 = + 0,02
День 3 = + 0,03
День 4 = + 0,04

Чтобы в итоге сложить все это так:

 1 + 2 + 3 + 4 + 5 + 6 + ... = 66795

Реальный вопрос: какова простая формула для получения суммы последовательных целых чисел, начиная с целого числа 1, без необходимости все это подсчитывать?!

суммирование
арифметика

$\endgroup$

$\begingroup$

На самом деле вопрос в том, какая простая формула для получения суммы последовательных целых чисел, начиная с целого числа 1, без необходимости подсчитывать все это

В то время как другие ответили на вопрос, я не мог удержаться, чтобы отразить некоторые истории, связанные с вопросом.

Вопрос, который вы задали, относится к известному математику Гауссу, история, которую иногда называют «Наказанием Гаусса», звучит так:

В начальной школе в конце 1700-х годов Гаусса попросили найти сумма чисел от 1 до 100. Вопрос был поставлен как «занят работу» учителем, но Гаусс довольно быстро нашел ответ, обнаружение закономерности. Его наблюдение было следующим:
1 + 2 + 3 + 4 + … + 98 + 99 + 100
Гаусс заметил, что если он разобьёт числа на две группы (1 до 50 и от 51 до 100), он мог сложить их вместе по вертикали, чтобы получить сумма 101.

1 + 2 + 3 + 4 + 5 + … + 48 + 49 + 50
100 + 99 + 98 + 97 + 96 + … + 53 + 52 + 51
1 + 100 = 101 2 + 99 = 101 3 + 98 = 101 . . . 48 + 53 = 101 49 + 52 = 101 50 + 51 = 101
Гаусс понял, что его окончательная сумма будет 50(101) = 5050.

Источник вышеизложенного в основном из Сумма первых 100 целых чисел

Другая версия звучит так, он написал цифры так:

001 + 002 + 003 +. ..+ 098 + 099 + 100 = S

100 + 099 + 098 +…+ 003 + 002 + 001 = S

(100+1)+(100+1)+(100+1)+…+ (100+1)+ (100+1)+(100+1)= 2S

Значение $(100+1)$ повторяется $100$ раз.

получаем:

100$ * (100+1) = 2S$$

, но нам нужно только значение $S$

$$s=\frac{100*(100+1)}{2}$$

Излишне говорить, что число 100 может быть любым положительным целым числом, а метод будет работать так же. Удивительно, что творится в голове у маленького ребенка!

$\endgroup$

$\begingroup$

В последнее время многие друзья спрашивают об этом, так как это во всем Фейсбук . Формула на самом деле довольно проста:

 (N (N + 1)) / 2, где N = максимальное значение.

Или просто $\frac {n(n+1)}{2}$

Таким образом,

 365 (365 + 1) ) / 2 = 66795

Разделите это на 100 ( потому что в одном долларе 100 пенни ) и альт! 667,95 $

Это СТАРАЯ математика (вспомните 6 век до н. э.), в которой эти результаты обозначаются как треугольник числа . Отчасти потому, что, складывая их, вы можете сложить результаты в форме треугольника!

 1 = 1
     *
1 + 2 = 3
     *
    * *
1 + 2 + 3 = 6
     *
    * *
   * * *
1 + 2 + 3 + 4 = 10
     *
    * *
   * * *
  * * * *

NoChance тоже имеет забавную историю, а ответит на этот вопрос!
Немного информации о его уроке: _{-{для супер-ботаников!}-}
» …Говорят, что Карл Фридрих Гаусс нашел это соотношение в своей ранней юности, путем умножения n/2 пар чисел в сумме на значения каждой пары n+1. Однако независимо от истинности этого истории, Гаусс не был первым, кто открыл эту формулу, и некоторые находят вполне вероятно, что его происхождение восходит к пифагорейцам 5 века до н.э….» — wikipedia
«…Говорят, что математическое изучение фигурных чисел возникло с Пифагором, возможно, основанным на вавилонских или египетских предшественниках.
Создание любого класса фигурных чисел пифагорейцев изучение с помощью гномонов также приписывается Пифагору. К сожалению, нет надежного источника для этих утверждений, потому что все сохранившиеся сочинения о пифагорейцах написаны веками позже. Кажется быть уверенным, что четвертое треугольное число из десяти предметов, называемое tetractys на греческом языке был центральной частью пифагорейской религии, наряду с несколькими другими фигурами, также называемыми тетрактисами. фигурировать числа были проблемой пифагорейской геометрии. … — википедия

Видишь? Веселье, цифры!

$\endgroup$

$\begingroup$

Поскольку рост является линейным, средняя сумма также является средней суммой за первый и последний день, следовательно,

$$365\times\frac{0,01+3,65}2.$$

$\endgroup$

$\begingroup$

Вообще говоря, вы можете сложить любой равномерно распределенный набор чисел по формуле:

$(1+\frac{n_{2}-n_{1}}{i})(\frac {n_{2}+n_{1}}{2})$

Учитывая, что $i$ интервал между каждым числом, $n_1$ — меньшее число, а $n_2$ — большее число.

Например, если вы начали с 5 долларов, а затем, подсчитывая по два доллара за раз в течение недели (до 17 долларов), вы получите 77 долларов.

$(1+\frac{17-5}{2})(\frac {17+5}{2})$

$(1+\frac{12}{2})(\frac {22 {2})$

$(1+6)(11)$

$7(11)$

$77$

Вызов пенни следует той же формуле:

$(1+\frac{365-1}{1})(\frac {365+1}{2})$

$(1+364)(183)$

$(365)(183 )$

$66795$ (в пенни)

В то время как другие ответы сосредоточены на специализированном подмножестве этой формулы, я решил предоставить более общую форму формулы, которая полезна в различных ситуациях.

$\endgroup$

$\begingroup$

Пусть $S_1=1+2+3+….+(n-1)+n$,

и $S_2=n+(n-1)+(n-2)+…+2 +1$, должно быть ясно, что $S_1=S_2$

Сложение двух выражений дает $S_1+S_2=(n+1)+(n+1)+…+(n+1)$ имеется n членов, т.е. $2S_1=n(n+1)$ или $S_1=\frac{n(n+1)}{2}$

$\endgroup$

$\begingroup$

$1+2+3+. ..+(n-1)+n=\frac{1+2+3+…+(n-1)+n+1+2+3+… +(n-1)+n}{2}=\frac{(1+n)+(2+n-1)+(3+n-2)+…+(n+1)}{2 }=\frac{(n+1)+(n+1)+(n+1)+…+(n+1) \left[ n \mathrm{-times}\right]}{2}= \frac{n(n+1)}{2}$

$\endgroup$

$\begingroup$

Как указывали другие, ответ $\frac {n(n+1)}{2}$. Вот интуитивное доказательство:

Вы можете сгруппировать первое и последнее числа, сумма которых равна $n + 1$. Второй и предпоследний имеют сумму $n + 1$. Если продолжить в том же духе, то вы заметите, что все такие пары имеют сумму $n + 1$ — то есть потому, что первая увеличивается на $1$, вторая в паре — на $-1$. Сколько пар? $\frac{n}{2}$. Таким образом, общая сумма пар равна $\frac {n(n+1)}{2}$

$\endgroup$

$\begingroup$

Я удивлен, что никто не выложил решение с подсчетом рукопожатий. Если в комнате $N$ человек и все пожимают друг другу руки, сколько рукопожатий?

Считайте это двумя способами. Комната начинается с одного человека. Приходит номер $2$ и пожимает руку. Приходит число $3$ и трясет два, и так далее, так что общее число равно $1 + 2 + \cdots + (N-1)$.

Теперь посчитайте рукопожатия другим способом. Каждый из $N$ человек пожимает $N-1$ руки, но при этом каждое рукопожатие считается дважды, так что в сумме получается $N(N-1)/2$.

И посмотрите второе доказательство без слов здесь: http://artofproblemsolving.com/wiki/index.php?title=Proofs_without_words#Summations

$\endgroup$

$\begingroup$

Арифметическая прогрессия — это такая последовательность чисел, что разница $d$ между последовательными членами постоянна. Если первое слагаемое равно $a_1$, количество слагаемых равно $n$, а последнее слагаемое равно $a_n$, то вся сумма равна

$$ S = \frac{n \cdot (a_1 + a_n)}{2} $$

где

$$ a_n = a_1 + (n — 1) \cdot d $$

В вашем примере $ a_1 = 0,01$, $d = 0,01$, $n = 365$, поэтому

$$ a_{365} = 0,01 + (365 — 1) \cdot 0,01 = 3,65 $$

$$ S = \frac{365 \cdot (0. 01 + 3.65)}{2} = 667,95 $$

Если вы хотите использовать только $a_1$, $d$ и $n$, то единственная формула из обоих выше

$ $ S = \frac{n \cdot (2 \cdot a_1 + (n-1) \cdot d)}{2} $$

$$ S = \frac{365 \cdot (2 \cdot 0,01 + (356-1) \cdot 0,01)}{2} = 667,95 $$

$\endgroup$

Что такое год в математике? Определение, примеры, факты

Что такое год?

Год — это время, за которое Земля совершает один оборот вокруг Солнца. Год также можно описать как период из 12 месяцев (365 дней или 366 дней), начинающийся с первого января и заканчивающийся тридцать первым декабря.

Один полный календарный год также может быть выражен как

С 4 июля текущего года по 4 июля следующего года
Рождества этого года до Рождества следующего года
От вашего последнего дня рождения до следующего дня рождения

Связанные игры

Определение года

Год — это время, за которое Земля совершает один оборот вокруг Солнца. Это период в 12 месяцев, отсчитываемый от любой конкретной даты.

Связанные рабочие листы

Обычный год и високосный год

Сколько дней в году? Мы обсудим это для двух случаев. Существует два типа года:

Обычный год

В обычном году 365 дней.

Високосный год

В високосном году 366 дней. Земля совершает оборот вокруг Солнца в среднем за 365,25 дня. Дни в календарном году обычно округляются до 365. Мы добавляем день в наш календарь каждые четыре года или около того, чтобы компенсировать потерянную часть дня. Это високосный год, когда к концу самого короткого месяца, т. е. к февралю, прибавляется лишний день. Вставочный день — это название, данное этому дню, обычно называемому Високосным днем, 29 февраля..

Сколько месяцев в году?

В году 12 месяцев. Названия месяцев:

Количество дней в году

Первый день года — 1 января, последний день — 31 декабря.

В обычном году семь месяцев по 31 дню, 4 месяца по 30 дней и 1 месяц по 28 дней.

Количество дней в обычном году $= (7 х 31) + (4 х 30) + (1 х 28)$

$= 217 + 120 + 28 $

$= 365$ дней

Количество дней в високосном году $= (7 х 31) + (4 х 30) + (1 х 29)$

$= 217 + 120 + 29 $

$= 366$ дней

Среднее количество недель в году

Продолжительность полного оборота Земли по отношению к Солнцу определяется как один день. Земля вращается вокруг своей оси один раз в 24 часа.

В неделе 7 дней:

Понедельник, вторник, среда, четверг, пятница, суббота и воскресенье.

В году 365 или 366 дней в зависимости от того, обычный это год или високосный. Итак, сколько недель в году? Давай выясним.

Количество недель в обычном году $= \frac{365}{7} = 52$ недель $+ 1$ день

Количество недель в високосном году $= \frac{366}{7} = 52$ недели $+ 2$ дни

Забавные факты

В астрономии год по юлианскому календарю — это единица измерения времени, которая определяется как ровно 365,25 дня по 86400 секунд СИ каждый.
Лунный год состоит из двенадцати полных циклов фаз Луны (примерно 354 дня).
Галактический год , также известный как космический год, определяется как продолжительность времени, необходимого Солнцу для одного оборота вокруг центра Галактики Млечный Путь.
Финансовый или финансовый год — это 12-месячный период для расчета годовой финансовой отчетности предприятий и других организаций
Годовой период, в течение которого учащийся посещает учебное заведение, известен как учебный год . Он может быть разделен на семестры или четверти.
Если сегодня понедельник, он снова будет понедельником через 7 дней, так как 7-дневный цикл повторяется.

Как проверить, какой год является високосным

Шаг 1: Проверить, делится ли год на 4.

Если нет, то это не високосный год.

Пример: 2017 год не високосный.

Шаг 2: Если год делится на 4, а также делится на 100, это не високосный год.

Пример: 2300 год не високосный.

Шаг 3: Если год делится на 4, а также делится на 400, это високосный год.

Пример: 1600, 2000 високосные годы.

10 лет, 100 лет, 1000 лет

10 лет составляют одно десятилетие.
100 лет составляют один век. Значение 100 лет также можно описать с помощью слова «столетие». Столетие – это сотая годовщина какого-либо события.
1000 лет составляют одно тысячелетие.

Годы с 1800 по 1899 называют девятнадцатым веком.

Годы с 2000 по 2099 называют двадцать первым веком.

Заключение

В этой статье мы узнали про год. Год – это определенный период времени, состоящий из 365 или 366 дней. Давайте рассмотрим несколько примеров и попрактикуемся в решении задач.

Решенные примеры для года

1. Расположите месяцы года в правильном порядке. Сколько месяцев составляет год?

Решение:

В году 12 месяцев.

Правильный порядок месяцев:

Январь, февраль, март, апрель, май, июнь, июль, август, сентябрь, октябрь, ноябрь и декабрь.

2. Сколько дней в первых 6 месяцах обычного года?

Решение:

Первые 6 месяцев: январь, февраль, март, апрель, май, июнь.

Количество дней в январе $= 31$

Количество дней в феврале $= 28$

Количество дней в марте $= 31$

Количество дней в апреле $= 30$

Количество дней в мае $= 31$

Количество дней в Июнь $= 30$

Количество дней в первые 6 месяцев $= (3 х 31) + (2 х 30) + (1 х 28) = 93 + 60 + 28$

$= 181$ дней

3. Проверить, является ли 2070 год високосным или нет.

Решение:

$2070 \div 4 = 517,5$, что означает, что 2070 не делится полностью на 4.

Итак, год не високосный.

4. Сколько месяцев по 31 дню в году?

Решение:

Месяцы по 31 дню $=$ Январь, март, май, июль, август, октябрь, декабрь.

Количество месяцев, в которых 31 день $= 6$

5. Если сегодня суббота, какой день будет через 50 дней?

Решение:

Каждый день недели повторяется через 7 дней.

Итак, после 49дней, это будет суббота.

$\these$ Через 50 дней будет воскресенье.

Практические задачи

Что из следующего является лишним?

июнь

сентябрь

ноябрь

декабрь

Правильный ответ: декабрь
Все месяцы, кроме декабря, состоят из 30 дней.

Сколько дней в високосном году?

354

365

366

364

Правильный ответ: 366
В високосном году 366 дней.

Сколько недель в обычном году?

52 недели $+ 1$ дней

53 недели

52 недели $+ 2$ дней

54 недели

Правильный ответ: 52 недели $+ 2$ дней
Количество дней в обычном году $= 365 $ Количество дней в неделе $= 7$ Количество недель $= \frac{365}{7} = 52$ недель $+ 1$ день

Какой из следующих годов является високосным?

500

800

100

1000

Правильный ответ: 800
Только 800 точно делится на 400. Итак, 800 — високосный год.
500, 100, 1000 делятся на 100. Таким образом, это не високосные годы.

Если завтра среда, то какой был позавчера?

Суббота

Воскресенье

Понедельник

Пятница

Правильный ответ: Воскресенье
Завтра среда.
Сегодня вторник. 904:90 Вчера был понедельник.
Позавчера было воскресенье.

Часто задаваемые вопросы по году

Как называется пятилетний период?

Период в 5 лет известен как Lustrum.

Что такое год?

Год используется для обозначения возраста человека. Например, если кому-то или чему-то пятнадцать лет, они жили или существовали пятнадцать лет.

Какое другое слово используется для «года»?

Другим словом, используемым для обозначения года, является год.

Какое слово использовалось в течение десяти тысяч лет?

Мы используем декамиллениум для периода в десять тысяч лет.