Математика Часть I (решения) для 9 класса Математика Глава 5
- Решения для учебников
- Класс 9
- Математика
- линейные уравнения с двумя переменными
Математика Часть I (решения) Решения для 9 класса Математика Глава 5 Линейные уравнения с двумя переменными представлены здесь с простыми пошаговыми объяснениями. Эти решения для линейных уравнений с двумя переменными чрезвычайно популярны среди учащихся 9 класса по математике. Решения для линейных уравнений с двумя переменными пригодятся для быстрого выполнения домашних заданий и подготовки к экзаменам. Все вопросы и ответы из первой части математики (решения) Книга 9 классаМатематика Глава 5 предоставляется здесь для вас бесплатно.
Страница № 86:
Вопрос 1:
Используя переменные x и y , составьте любые пять линейных уравнений с двумя переменными.
Ответ:
Линейные уравнения с двумя переменными x и y будет
x+y=12x+3y=8x-y=65x-2y=3x+2y=3
Страница № 86:
Вопрос 2:
Напишите пять решений уравнения x + y = 7.
Ответ:
Данное уравнение x + y = 7.
Возможным решением является
| х | 0 | 7 | 1 | 6 | 4 |
| у | 7 | 0 | 6 | 1 | 3 |
Страница № 86:
Вопрос 3:
Решите следующие системы одновременных уравнений.
(i) х + у = 4; 2 х — 5 у = 1
(ii) 2 х + у = 5; 3 х — y = 5
(iii) 3 x — 5 y =16; x — 3 y = 8
(iv) 2 у — х = 0; 10 х + 15 у = 105
(v) 2 х + 3 у + 4 = 0; x — 5 y = 11
(vi) 2 x -7 y = 7; 3 x + y = 22
Ответ:
(i) x + y = 4 …..(I)
2 x — 5 y = 1 …..(II)
Из (I) имеем
x=4-y
. 5y=1⇒8-2y-5y=1⇒8-7y=1⇒8-1=7y⇒7=7y⇒y=1
Подставив значение y в (I), мы получим
x+1= 4⇒x = 3
Таким образом, x, y = 3,1
(ii) 2 x + y = 5 .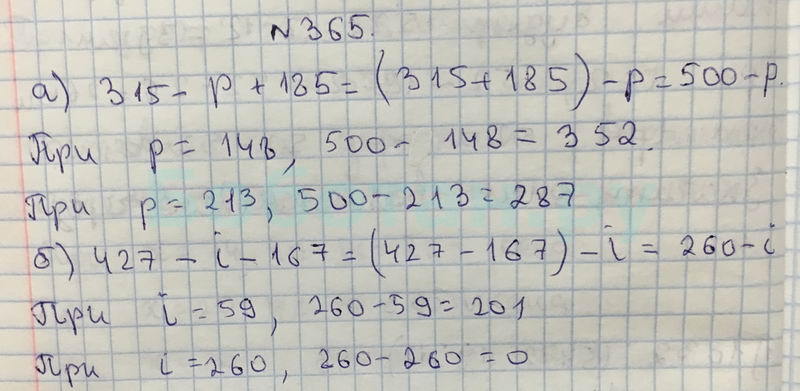
…. (i)
3 x — y = 5. ….(II)
Складываем (I) и (II)
5x=10⇒x=105=2
Подставляя это значение в (I), получаем
2×2+y=5⇒4+y=5⇒y=1x,y=2,1
(iii) 3 x — 5 y =16 …..(I)
x — 3 y = 8 …..(II)
Умножьте (II) на 3
3x-9y=24 …..(III)
(I) — (III)
4y =-8y=-2 Подставляя значение y в (II)x=2
(iv) 2 y — x = 0 ⇒ x=2y 2 …..(I)
10 x9 + 15 y = 105 …..(II)
Вычитание 5 обычных из (II)
2x+3y=21 …..(III)
Из (I) и (III)
22y+3y=21⇒4y+3y=21⇒7y=21⇒y=3x=2×3=6
(v) 2 x + 3 y + 4 = 0 ….. (i)
x -5 y = 11 ….. (ii)
от (i) мы иметь
2 x + 3 y = -4 ….. (iii)
Умножение (II) с 2
2x-10y = 22 .
…. (iv)
из (III) и ( IV) у нас есть
2 x + 3 y = -4
2x-10y = 22
(iii)-(iv)
13y = -26,y = -2
x = 11 + 5 Y
x = 1
(vi) 2 x -7 y = 7 ….. (i)
3 x + y = 22 ….. (ii)
Умножение (Multiply ( II) с 7
21 x + 7 y = 154 …..(III)
(I) + (III)
23 x = 161
x = 7, y = 1
Страница № 90:
Вопрос 1:
В конверте лежат банкноты номиналом 5 и 10 рупий. Общая сумма этих банкнот вместе составляет 350 рупий. Количество банкнот в 5 рупий меньше на 10, чем количество банкнот в 10 рупий. Затем найдите количество банкнот номиналом 5 и 10 рупий.
Ответ:
Отказ от ответственности: В данном вопросе есть ошибка. Вместо «Количество банкнот номиналом 5 рупий меньше на 10, чем количество банкнот номиналом 10 рупий»
предложение должно было быть «Количество банкнот в 5 рупий больше на 10, чем количество банкнот в 10 рупий».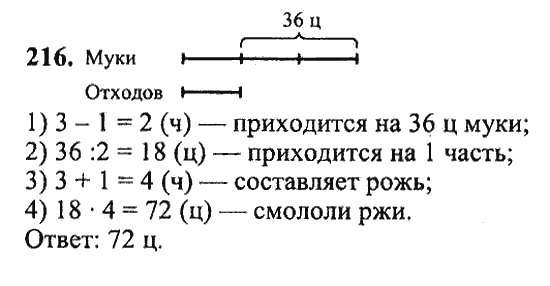
Пусть количество банкнот номиналом 5 рупий равно x , а количество банкнот номиналом 10 рупий равно y.
5x+10y = 350,x+2y = 70 ….. I
Номер из 5 нот рупии больше на 10, чем число из 10 нот рупии
Итак, x-y = 10
⇒x = 10+y .. …(II)
Из (I) и (II) имеем
10+y+2y=70⇒10+3y=70⇒3y=60⇒y=20
Таким образом, x = 10 + 20 = 30
Количество банкнот по 5 рупий = 30, количество банкнот по 10 рупий = 20
Страница № 90:
Вопрос 2:
в два раза больше его числителя. Если к числителю и знаменателю добавить 1 соответственно, отношение числителя к знаменателю будет 1 : 2. Найдите дробь.
Ответ:
Отказ от ответственности: В данном вопросе есть ошибка. При данных утверждениях два сформированных линейных уравнения будут одинаковыми.
Страница № 90:
Вопрос 3:
Сумма возрастов Приянки и Дипики составляет 34 года. Приянка старше Дипики на 6 лет.
Затем найдите их сегодняшний возраст.
Ответ:
Пусть возраст Приянки будет х лет, а возраст Дипики х лет.
Сумма возрастов Приянки и Дипики составляет 34 года.
x+y=34 …..(I)
Приянка старше Дипики на 6 лет.
x-y=6 …..(II)
Складывая (I) и (II), получаем
2x=40⇒x=20
Подставляя значение x в (I), получаем
y = 14
Таким образом, возраст Приянки = 20 лет и возраст Дипики = 14 лет.
Страница № 90:
Вопрос 4:
Общее количество львов и павлинов в определенном зоопарке равно 50. Общее количество их ног равно 140. Затем найдите количество львов и павлинов в зоопарке.
Ответ:
Пусть львов будет х 9.0020 и количество павлинов и .
Общее количество львов и павлинов в определенном зоопарке равно 50.
Итак, x+y=50 …..(I)
Общее количество их ног равно 140.
У льва 4 ноги, а у павлина 2.
4x+2y=140⇒2x+y=70 …..II
Вычитая (II) из (I), получаем
x=20y=30
Таким образом, число львов = 20, а павлинов = 30.
Страница № 90:
Вопрос 5:
Санджай получает фиксированный ежемесячный доход. Каждый год происходит определенная прибавка к его зарплате. Через 4 года его месячная зарплата составляла рупий. 4500, а через 10 лет его месячная зарплата стала 5400 рупий, затем найдите его первоначальную зарплату и ежегодную прибавку.
Ответ:
Пусть фиксированный месячный доход равен х рупий.
Годовой прирост составит и рупий.
Через 4 года его месячная зарплата составила рупий. 4500
Месячный оклад + ежегодная надбавка за 4 года = 4500
x+4y=4500 …..(I)
Через 10 лет его месячная зарплата составила 5400 рупий
Месячная зарплата + годовая прибавка за 10 лет = 5400
x+10y=5400 (Ii)- (i)
6 y = 900
y = 150
x = 4500- 150 × 4 = 3900
Таким образом, месячная зарплата = RS 3900
Годовой приращение = RS 150
.
Страница № 90:Вопрос 6:
Цена 3 стульев и 2 столов 4500 рупий, а цена 5 стульев и 3 столов 7000 рупий, затем найдите цену 2 стульев и 2 столов.
Ответ:
Пусть цена 1 стула x рупий, а цена 1 стола рупий y.
Цена за 3 стула и 2 стола 4500 рупий
3x+2y=4500 …..I
Цена за 5 стульев и 3 стола 7000 рупий
5x+3y=7000 …..II
Умножить (I) с 3 и (II) с 2
9x+6y=13500 …..III10x+6y=14000 …..IVIV-IIIx=500. Подставим это значение x в I3×500+2y=4500⇒ 1500+2г=4500⇒2г=4500-1500=3000⇒г=1500
Цена 2 стульев и 2 столов составит
=2x+2y=2x+y=2500+1500=2×2000=4000
Таким образом, цена 2 стульев и 2 столов составит 4000 рупий
Страница № 91:
Вопрос 7:
Сумма цифр двузначного числа равна 9. Число, полученное перестановкой цифр, больше исходного числа на 27. Найдите двузначное число.
Ответ:
Пусть на месте десятков будет х , а на месте единиц у .
Полученное число = 10 x + y
Сумма цифр двузначного числа равна 9.
x+y=9 …..(I) исходное число на 27.
10y+x-10x + y=27⇒10y+x-10x-y=27⇒9y-9x=27⇒y-x=3 ….. II
Добавление (I) и (II)
2y=12⇒y=6
x = 3
Таким образом, число равно 36.
Страница № 91:
Вопрос 8:
В ∆ABC мера угла A равна сумме мер ∠ B и ∠ C. Также отношение мер ∠ B и ∠ C равно 4 : 5. Тогда найдите меры углов треугольника .
Ответ:
∠A = ∠B + ∠C …..(I)
∠B∠C=45⇒5∠B=4∠C ….. II
Мы знаем по свойству суммы углов ,
∠A + ∠B + ∠C = 180°
Из (I)
∠B + ∠C +∠B + ∠C = 180°
⇒2∠B+∠C=180°⇒2∠B+5∠ B4=180°⇒∠B+5∠B4=90°⇒4∠B+5∠B=360°⇒9∠B=360°⇒∠B=40°
5×40°=4∠C⇒∠C =50°
И ∠A = ∠B + ∠C = 40°+50°=90°.
Страница № 91:
Вопрос 9:
Разделите веревку длиной 560 см на 2 части так, чтобы удвоенная длина меньшей части равнялась 13 большей части.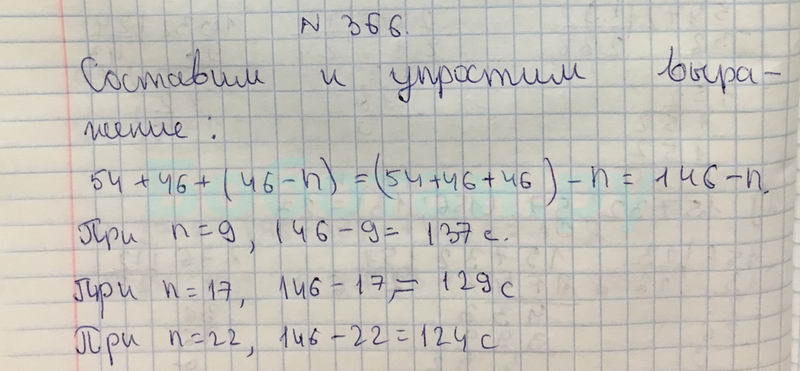
Затем найдите длину большей части.
Ответ:
Пусть меньшая часть будет х см, а большая х см.
x+y=560 …..(I)
Удвоенная длина меньшей части равна 13 большей части.
x=13y⇒3x=y
Подставив значение y в (I), мы получим
x+3x=560⇒4x=560⇒x=140
Таким образом, y=3×140=420
Таким образом, большая часть = 420 см, а меньшая часть 140 см.
Страница № 91:
Вопрос 10:
На конкурсном экзамене было 60 вопросов. За правильный ответ начисляется 2 балла, за неправильный ответ снимается 1 балл. Яшвант ответил на все вопросы и получил в общей сложности 90 баллов. Тогда в скольких вопросах он ошибся?
Ответ:
Пусть количество правильных ответов равно x , а количество неправильных ответов равно y.
Всего ответов = Количество правильных + количество неправильных = 60
x+y=60 …..(I)
Всего полученных баллов = 90
2x-y=90 .
….(II)
Добавление (I) и (II) мы имеем
3x=150⇒x=50y=10
Количество вопросов, на которые он ответил неправильно, равно 10.
Номер страницы 91:
Вопрос 1:
Выберите правильные альтернативные ответы на следующие вопросы. вопросы.
(i) Если 3 x + 5 y = 9 и 5 x + 3 y = 7, то каково значение x + 0y?
(A) 2 (B) 16 (C) 9 (D) 7
(ii) «Если из длины и ширины прямоугольника вычесть 5, периметр станет равен 26». Какова математическая форма утверждения?
(А) х — у = 8 (Б) х + у = 8 0020 + y = 23 (D) 2 x + y = 21
(iii) Аджай моложе Виджая на 5 лет. Сумма их возрастов 25 лет. Сколько лет Аджаю?
(A) 20 (B) 15 (C) 10 (D) 5
Ответ:
(i) 3 x + 5 y = 9 …..(I) 9 x + 3 y = 7 .
….(II)
Складывая (I) и (II), получаем
8x+8y=16⇒x+y=2
Следовательно, правильный ответ – вариант (A) .
(ii) Пусть длина будет x , а ширина y .
Периметр прямоугольника = 2( l + b ) = 26
2( l + b ) = 26
⇒ 2x-5+y-5=26⇒2x+y-10=26 ⇒ 2x+y-10=26
⇒x+y=23
Следовательно, правильный ответ — вариант (C).
(iii) Пусть возраст Аджая будет х лет, а возраст Виджая будет х лет.
Аджай моложе Виджая на 5 лет.
y-x=5 …..I
Сумма их возрастов составляет 25 лет.
x+y=25 …..II
Складывая (I) и (II), мы получаем
2y=30⇒y=15x=10
Таким образом, возраст Аджая составляет 10 лет.
Следовательно, правильный ответ — вариант (С).
Страница № 91:
Вопрос 2:
Решите следующие одновременные уравнения.
(i) 2 х + у = 5 ; 3 x — y = 5
(ii) x -2 y = -1 ; 2 х — у = 7
(iii) x + y = 11; 2 x — 3 y = 7
(iv) 2 x + y = -2 ; 3 x — y = 7
(v) 2 x — y = 5 ; 3 x + 2 y = 11
(vi) x — 2 y = -2 ; x + 2 y = 10
Ответ:
(i) 2 x + y = 5 .
….(I)
3 x — y = 5 …..(II)
(I) + (II)
5x=10⇒x=2
Помещение значения x в (I)
2×2+y=5⇒4+y=5⇒y=1
(ii) x -2 y = -1 ..(I)
2 x — y = 7 …..(II)
Умножить (I) на 2
2x-4y=-2 0 …..(3III) 0 …..(3III) 0 ) из (II)
Подставляя значение y в (I) получаем
x-2×3=-1⇒x-6=-1⇒x=5
(iii) x + y = 11 ….. (I)
2 x — 3 y = 7 …..(II)
Умножить (I) на 3
3x+3y=33 …..(III)
Сложение (II) и (III)
5x=40⇒x=8
Подставляя значение x в (I)
8+y=11⇒y=3
(iv) 2 x + y = -2 . ….(I)
3 x — y = 7 …..(II)
Сложение (I) с (II)
5x=5⇒x=1
Подстановка значения x в (I)
2×1+y=-2⇒2+y=-2⇒y=-4
(v) 2 x — y = 5 .
…. (i)
3 x + 2 y = 11 ….. (ii)
4x-2y=10 …..(III)
Складываем (II) с (III)
7x=21⇒x=3
Подставляя значение x в (I), получаем
2×3-y=5⇒6-y=5⇒y=1
(vi) x — 2 y = -2 …..(I)
x + 2 y = 10 …..(II)
Сложение (I) ≥ 9×0 с (3)
Подставляя значение x в (I), получаем решить следующие уравнения.
(i) 3 x — 4 y = 7; 5 x + 2 y = 3
(ii) 5 x + 7 y = 17 ; 3 х -2 у = 4
(iii) x -2 y = -10; 3 х — 5 у = -12
(iv) 4 х + у = 34 ; x + 4 y = 16
Ответ:
(I) 3 x -4 y = 7 ….. (i)
5 x + 2 y = 3 .
Умножить (II) на 2
10 x 9у 1-4y=7⇒3-4y=7⇒y=-1
Таким образом, x = 1 и y=-1.
(ii) 5 x + 7 y = 17 ….. (i)
3 x -2 y = 4 ….. (ii)
Умножение (i) с 3 и (II) с 5
15 x + 21 y = 51 …..(III)
15 x -10 y = 20 …..(IV)
Вычитая (IV) из (III), получаем ) получаем
5x+7×1=17⇒5x=10⇒x=2
Таким образом, x=2, y=1.
(iii) x -2 y = -10 …..(I)
3 x — 5 y = -12 …..(II)
с умножением 3
3x-6y=-30 …..(III)
Вычитая (II) из (III) получаем
-y=-18⇒y=18
Подставляя значение y в (I) получаем
x-2×18=-10⇒x=-10+36=26
Таким образом, x=26,y=18
(iv) 4 x + y = 34 …..(I)
….(II) Складывая (I) и (II) ⇒ 5+y=5+
0 =10 …..I
Вычитая (II) из (I), получаем
3x-3y=18⇒x-y=6 …..IV
(III) + (IV)
2x=16⇒x= 8
Подставляя значение x в (I), получаем
48+y=34⇒y=34-32=2⇒y=2
Таким образом, x=8,y=2
Страница № 91:
Вопрос 4:
Решите следующие одновременные уравнения.
(i) x3 + y4 = 4 ; x2 — y4= 1
(ii) x3 + 5y = 13 ; 2x + y2 = 19
(iii) 2x + 3y = 13 ; 5x — 4y = -2
Ответ:
(i) x3 + y4 = 4 …..(I)
x2 — y4= 1 …..(II)
Умножение (I) с НОК 3 и 4, что равно 12, мы получаем
4x+3y=48 …..(III)
Умножая (II) на LCM 2 и 4, что равно 4, мы получаем
2x-y=4 …..(IV)
4x-2y=8 …..(V)
Вычитание (V) из (III)
5y=40⇒y =8
Подставляя это значение y в (IV), получаем 19 .
….II ⇒x+15y=39 …..III4x+y=38 …..IV
Умножая (III) на 4, получаем
4x+60 y = 15 (V)
Вычитание (IV) из (V)
59y=118⇒y=2
Подставляя значение y в (IV), получаем
4x+2=38⇒4x=36⇒x=9
(iii) 2x + 3y = 13 ; 5x — 4y = -2
Пусть 1x=u и 1y=v
Таким образом, получаем следующие уравнения: 15v=65 …..III10u-8v=-4 …..IVВычитание IV из III23v=69⇒v=3Подстановка значения v в I2u+3×3=13⇒2u=4⇒u=21x= u⇒x=1u=121y=v⇒y=1v=13
Номер страницы 92:
Вопрос 5:
Двузначное число в 3 раза больше суммы своих цифр. Если к этому числу добавить 18, сумма будет равна числу, полученному путем перестановки цифр. Найдите число.
Ответ:
Пусть двузначное число равно 10 х + у.
Двузначное число в 3 раза больше суммы своих цифр.
10x+y=4x+y+3⇒10x+y=4x+4y+3⇒2x-y=1 …..I
Если к этому числу добавить 18, сумма будет равна числу, полученному меняя местами цифры.
10x+y+18=10y+x⇒9x-9y=-18⇒x-y=-2 …..II
(I) — (II)
x=3,y=5
Таким образом, полученное число составляет 35.
Страница № 92:
Вопрос 6:
Общая стоимость 6 книг и 7 ручек составляет 79 рупий, а общая стоимость 7 книг и 5 ручек составляет 77 рупий. Найдите стоимость 1 книги и 2 ручек.
Ответ:
Отказ от ответственности: В данном вопросе есть ошибка. Вместо 7 книг и 5 ручек должно быть 7 книг и 6 ручек.
Пусть стоимость 1 книги будет
Общая стоимость 6 книг и 7 ручек 79 рупий.
6x+7y=79 …..I
Общая стоимость 7 книг и 6 ручек составляет 77 рупий.
7x+6y=77 …..II
Сложение (I) и (II)
13x+13y=156⇒x+y=12 …..III
Вычитание (II) из (I)
x-y =-2 …..IV
Добавление (III) и (IV)
2x=10⇒x=5
y = 7
Стоимость 1 книги и 2 ручек составляет 5 + 14 = 19 рупий.
.
Страница № 92:
Вопрос 7:
Соотношение доходов двух человек 9 : 7. Соотношение их расходов 4 : 3. Каждый человек сберегает 200 рупий, найдите доход каждого.
Ответ:
Пусть доходы двух лиц равны x и y.
xy=97⇒7x=9y⇒7x-9y=0 …..I
Сбережения двух лиц = 200 рупий
Расходы = Доход — Сбережения
x-200y-200=43⇒3x-600=4y- 800⇒3x-4y=-200 …..II
21x-27y=0 …..III21x-28y=-1400 …..IVIV-III-y=-1400⇒y=1400
Подставляя значение y в (I), получаем
x = 1800
Таким образом, доход двух лиц составляет 1800 и 1400 рупий. ед., то площадь прямоугольника уменьшилась на 8 кв. Если длину уменьшить на 3 единицы, а ширину увеличить на 2 единицы, то площадь прямоугольника увеличится на 67 квадратных единиц. Затем найдите длину и ширину прямоугольника.
Ответ:
Пусть длина l , а ширина b .
Площадь прямоугольника = фунтов
Длина прямоугольника уменьшилась на 5 единиц, а ширина увеличилась на 3 единицы, тогда площадь прямоугольника уменьшилась на 8 квадратных единиц.
l-5b+3=lb-8⇒lb-5b+3l-15=lb-8⇒3l-5b=7 …..I
Если длина уменьшается на 3 единицы, а ширина увеличивается на 2 единицы, тогда площадь прямоугольника увеличится на 67 кв.
Умножить (I) на 2 и (II) на 3
6l- 10b=14 …..III6l-9b=219 …..IV III-IVb=205
Подставляя это значение в (I), получаем
3l-5205=7⇒3l=7+1025=1032⇒l =344
Таким образом, длина = 344 единицы, а ширина = 205 единиц.
Страница № 92:
Вопрос 9:
Расстояние между двумя точками A и B по дороге составляет 70 километров. Одна машина отправляется из А, а другая из Б. Если они едут в одном направлении, то встретятся через 7 часов. Если они едут навстречу друг другу, то встретятся через 1 час, затем найдите их скорости.
Ответ:
Пусть скорость более быстрого автомобиля будет х км/ч, а скорость более медленного автомобиля будет х км/ч.
Общее расстояние между ними 70 км.
Speed=DistanceTime
Когда обе машины едут в одном направлении, они встретятся через 7 часов.
Общая скорость = x − y
x-y=707⇒x-y=10 …..I x+y=70 …..II
Сложение (I) и (II)
2x=80⇒x=40
Подстановка значения x в (I)
40-y=10⇒y=40-10=30
Таким образом, скорость автомобилей 40 км/ч и 30 км/ч.
Страница № 92:
Вопрос 10:
Сумма двузначного числа и числа, полученного перестановкой его цифр, равна 99. Найдите число.
Ответ:
Пусть двузначное число будет 10 x + y .
Число, полученное при замене цифр = 10 г + х .
Сумма двузначного числа и числа, полученного путем перестановки его цифр, равна 99.
10 x + y + 10 y + x = 99
⇒ y=9x+1 =9
С заданной информацией можно составить только одно уравнение.
Таким образом, число может быть
18, 81, 54, 45, 27, 72, 36, 63.
20 сложных, но забавных вопросов по математике для начальной школы Бухгалтер, скорее всего, математика в начальной и средней школе была проклятием твоего существования. Вы бы неделями неустанно готовились к этим дурацким стандартизированным тестам — и все же, наступая в день экзамена, вы все равно не имели бы ни малейшего представления о том, для чего нужны какие-либо уравнения или сложные математические задачи. Поверьте нам, мы поняли.
Хотя логика может привести вас к мысли, что ваши математические способности естественным образом улучшились с возрастом, к сожалению, реальность такова, что, если вы не решаете задачи по алгебре и геометрии ежедневно, скорее всего, произойдет обратное. случай.
Не верите нам? Затем испытайте свою мудрость в вычислении чисел с помощью этих хитрых математических вопросов, взятых прямо из школьных тестов и домашних заданий, и убедитесь в этом сами.
1.
Вопрос: Какой номер парковочного места занимает автомобиль?Эта сложная математическая задачка стала вирусной несколько лет назад после того, как появилась на вступительном экзамене в Гонконге… для шестилетних детей. Предположительно, у студентов было всего 20 секунд, чтобы решить задачу!
Ответ: 87.
Хотите верьте, хотите нет, но этот «математический» вопрос вообще не требует математики. Если вы перевернете изображение вверх ногами, то увидите, что имеете дело с простой числовой последовательностью.
2. Вопрос: Замените вопросительный знак в приведенной выше задаче соответствующим номером.
Эта проблема не должна быть слишком сложной для решения, если вы много играете в судоку.
Ответ: 6.
Все числа в каждой строке и столбце в сумме дают 15! (Кроме того, 6 — единственное число, не представленное среди чисел от 1 до 9.)
3. Вопрос: Найдите эквивалентное число.
Эта задача взята прямо из стандартного теста, проведенного в Нью-Йорке в 2014 году.
Ответ: 9.
ShutterstockПростите, если вы не помните точно, как работают экспоненты. Чтобы решить эту задачу, вам просто нужно вычесть показатели степени (4-2) и решить для 3 2 , что расширяется до 3 x 3 и равняется 9.
4. Вопрос: Сколько маленьких собак заявлено для участия в выставке?
Изображение взято с Imgur/zakiamonЭтот вопрос взят непосредственно из домашнего задания по математике второклассника. Угу.
Ответ: 42,5 собаки.
Чтобы вычислить, сколько маленьких собак участвует в соревнованиях, вы должны вычесть 36 из 49, а затем разделить полученный результат, 13, на 2, чтобы получить 6,5 собак, или количество соревнующихся больших собак. Но вы еще не закончили! Затем вам нужно прибавить 6,5 к 36, чтобы получить количество соревнующихся маленьких собак, которое равно 42,5. Конечно, на самом деле половина собаки не может участвовать в выставках собак, но ради решения этой математической задачи давайте предположим, что это возможно.
5. Вопрос: Найдите площадь красного треугольника.
Изображение с YouTubeЭтот вопрос использовался в Китае для выявления одаренных пятиклассников. Предположительно, некоторые из сообразительных студентов смогли решить это менее чем за одну минуту.
Ответ: 9.
Чтобы решить эту задачу, вам нужно понять, как работает площадь параллелограмма. Если вы уже знаете, как связаны площадь параллелограмма и площадь треугольника, то сложите 79 и 10, а затем вычтите 72 и 8, чтобы получить 9.должно иметь смысл, но если вы все еще запутались, посмотрите это видео на YouTube для более подробного объяснения.
6. Вопрос: Какой высоты стол?
Изображение с YouTubeYouTube-блогер MindYourDecisions адаптировал этот ошеломляющий математический вопрос из похожего на домашнее задание ученика начальной школы в Китае.
Ответ: 150 см.
Изображение с YouTube Поскольку одно измерение включает рост кошки и вычитает рост черепахи, а другое делает противоположное, вы можете просто вести себя так, как будто двух животных здесь нет.
Поэтому все, что вам нужно сделать, это сложить два измерения — 170 см и 130 см — вместе и разделить их на 2, чтобы получить высоту стола, 150 см.ae0fcc31ae342fd3a1346ebb1f342fcb
7. Вопрос: Если стоимость биты и бейсбольного мяча вместе взятых составляет 1,10 доллара, а бита стоит на 1 доллар больше, чем мяч, сколько стоит мяч?
ShutterstockЭта задача с математической точки зрения очень похожа на одну из других в этом списке.
Ответ: 0,05 доллара США.
Вспомните задачу о собаках на выставке собак и используйте ту же логику для решения этой задачи. Все, что вам нужно сделать, это вычесть 1,00 доллара из 1,10 доллара, а затем разделить этот результат, 0,10 доллара, на 2, чтобы получить окончательный ответ, 0,05 доллара.
8. Вопрос: Когда у Шерил день рождения?
Изображение через Facebook/Kenneth KongЕсли у вас возникли проблемы с чтением, см. здесь:
«Альберт и Бернард только что подружились с Шерил, и они хотят знать, когда у нее день рождения.
Шерил дает им список из 10 возможных Даты.
мая 15 мая 16 мая 19
июня 17 июня 18
14 июля 16 июля
14 августа 15 августа 17
Шерил затем рассказывает Альберту и Бернарду отдельно месяц и днем ее дня рождения. 9.
.
.0013
Альберт: Я не знаю, когда день рождения Шерил, но я знаю, что Бернард тоже не знает.
Бернард: Сначала я не знал, когда день рождения Шерил, но теперь я знаю.
Альберт: Тогда я также знаю, когда у Шерил день рождения.
Итак, когда у Шерил день рождения?»
Непонятно, почему Шерил не могла просто сказать Альберту и Бернарду месяц и день своего рождения, но это не имеет отношения к решению этой проблемы.
Ответ: 16 июля.
Запутался о том, как можно найти какой-либо ответ на этот вопрос? Не волнуйтесь, так было в большинстве стран мира, когда несколько лет назад этот вопрос, взятый из математической олимпиады в Сингапуре и Азии, стал вирусным. New York Times шаг за шагом объясняет, как добраться до 16 июля, и вы можете прочитать их подробный вывод здесь.
9. Вопрос: Найдите пропущенную букву.
Изображение получено через Facebook/The Holderness FamilyЭто взято из домашнего задания первоклассника .
Ответ: пропущена буква J.
Если сложить вместе значения, указанные для S, B и G, сумма получится равной 40, а добавление пропущенной буквы J (значение которой равно 14) дает сумма других диагоналей такая же.
10. Вопрос: Решите уравнение.
Изображение с YouTubeЭта задача может показаться простой, но удивительное количество взрослых не могут решить ее правильно.
Ответ: 1.
Начните с решения части уравнения, относящейся к делению. Для этого, если вы забыли, вам нужно перевернуть дробь и переключиться с деления на умножение, получив таким образом 3 x 3 = 9. Теперь у вас есть 9 – 9 + 1, и оттуда вы можете просто работать слева направо. вправо и получите окончательный ответ: 1.
11. Вопрос: Где следует провести линию, чтобы приведенное ниже уравнение было точным?
5 + 5 + 5 + 5 = 555.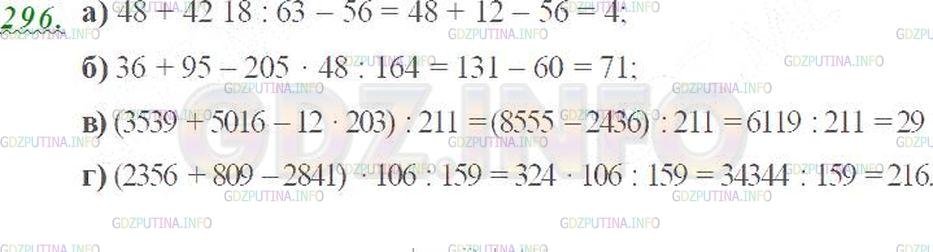
Ответ: Над знаком «+» следует провести черту.
Когда вы проводите наклонную линию в верхнем левом квадранте знака «+», она становится цифрой 4, и, таким образом, уравнение принимает вид 5 + 545 + 5 = 555.
12. Вопрос: Решите незаконченное уравнение.
Попробуйте выяснить, что общего у всех уравнений.
Ответ: 4 = 256.
Формула, используемая в каждом уравнении, составляет 4 x = Y. SO, 4 1 = 4, 4 2 = 16, 4 2 = 16, 4 2 = 16, 4 3 2 = 16, 4 3 2 = 16, 4, 4 2
= 16, 4, 4 2 = 64 и 4 4 = 256.13. Вопрос: Сколько треугольников на изображении выше?
Когда Best Life впервые написали об этом обманчивом вопросе, нам пришлось просить математика объяснить ответ!
Ответ: 18.
Некоторых людей смущают треугольники, спрятанные внутри треугольников, а другие забывают включить гигантский треугольник, в котором заключены все остальные. В любом случае, очень немногим людям — даже учителям математики — удалось найти правильный ответ на эту проблему. А чтобы получить дополнительные вопросы, которые проверят ваше предыдущее образование, ознакомьтесь с этими 30 вопросами, которые вам нужно будет ответить на высший балл, чтобы сдать экзамен по географии в 6-м классе.
14. Вопрос: Добавьте 8.563 и 4.8292.
Сложить два десятичных знака проще, чем кажется.
Ответ: 13.3922.
Пусть вас не смущает тот факт, что в 8.563 меньше номеров, чем в 4.8292. Все, что вам нужно сделать, это добавить 0 в конце 8,563, а затем добавить, как обычно.
15. Вопрос: На озере есть кувшинки. Каждый день заплата удваивается в размере…
Shutterstock… Если заплата покроет все озеро за 48 дней, сколько времени потребуется, чтобы заплата покрыла половину озера?
Ответ: 47 дней.
Большинство людей автоматически предполагают, что половина озера будет покрыта за половину времени, но это предположение неверно. Поскольку участок площадок удваивается в размере каждый день, озеро будет покрыто наполовину всего за один день до того, как оно покроется полностью.
16. Вопрос: Сколько футов в миле?
Эта задачка для начальной школы требует не столько решения проблем, сколько запоминания.
Ответ: 5280.
Это был один из вопросов, представленных в популярном шоу Вы умнее пятиклассника?
17. Вопрос: При каком значении «x» приведенное ниже уравнение верно?
Shutterstock-15 + (-5x) = 0
Ответ: -3.
Вам простительно думать, что ответ равен 3. Однако, поскольку число рядом с x отрицательное, нам нужно, чтобы x также было отрицательным, чтобы получить 0. Следовательно, x должно быть -3.
18. Вопрос: Сколько 1,92 разделить на 3?
Возможно, вам придется попросить помощи у детей.
Ответ: 0,64.
Чтобы решить эту, казалось бы, простую задачу, нужно убрать десятичную дробь из числа 1,92 и вести себя так, будто ее нет. После того, как вы разделили 192 на 3, чтобы получить 64, вы можете вернуть десятичную запятую на место и получить окончательный ответ 0,64.
19. Вопрос: Решите приведенное выше математическое уравнение.
Изображение с YouTubeНе забывайте о PEMDAS!
Ответ: 9.
Используя PEMDAS (аббревиатура, указывающая порядок, в котором вы решаете: «круглые скобки, показатели степени, умножение, деление, сложение, вычитание»), вы сначала должны решить сложение внутри скобок (1 + 2 = 3), и оттуда закончите уравнение, как оно написано слева направо.
20. Вопрос: Сколько здесь зомби?
Чтобы найти ответ на этот последний вопрос, потребуются дроби.
Ответ: 34.
Поскольку мы знаем, что на каждых трех человек приходится два зомби и что 2 + 3 = 5, мы можем разделить 85 на 5, чтобы вычислить, что всего существует 17 групп людей и зомби.