Категории: 5 класс.

Математика 5 класс виленкин 457: Номер №457, Часть 2 — ГДЗ по Математике 5 класс: Виленкин Н.Я.

 Комментировать

Содержание

Номер №457 — ГДЗ по Математике 5 класс: Виленкин Н.Я.

войтирегистрация

  1. Ответкин
  2. Решебники
  3. 5 класс
  4. Математика
  5. Виленкин
  6. Номер №457

НАЗАД К СОДЕРЖАНИЮ

2013г.ВыбранВыбрать ГДЗ (готовое домашние задание из решебника) на Номер №457 по учебнику Математика. 5 класс : учебник для учащихся общеобразовательных учреждений / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 31 издание 2013г.

2019г.ВыбранВыбрать ГДЗ (готовое домашние задание из решебника) на Номер №457 по учебнику Математика. 5 класс : учебник для учащихся общеобразовательных организаций / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 37 издание 2019г.

Условие 20132019г.

Cменить на 2013 г.

Cменить на 2019 г.

От деревни до города велосипедист ехал 4 ч со скоростью 12 км/ч. Сколько времени он потратит на обратный путь по той же дороге, если увеличит скорость на 4 км/ч?

От деревни до города велосипедист ехал 4 ч со скоростью 12 км/ч. Сколько времени он потратит на обратный путь по той же дороге, если увеличит скорость на 4 км/ч?

Решение 1

Решение 1

Решение 2

Решение 2

Решение 3

Решение 3

ГДЗ по Математике 5 класс: Виленкин Н.Я.

Издатель: Виленкин Н.Я. Жохов В.И. Чесноков А.С. Шварцбурд С.И. 2013/2019г.

ГДЗ по Математике 5 класс: Мерзляк А. Г.

Издатель: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. 2014-2018г.

ГДЗ по Математике 5 класс: Никольский С.М.

Издатель: С.М. Никольский, М.К, Потапов, Н.Н. Решетников А.В. Шевкин. 2015-2021г

ГДЗ по Математике 5 класс: Дорофеев Г.В.

Издатель: Г.В. Дорофеев, И.Ф. Шарыгин, С.Б. Суворова. 2017-2019г.

ГДЗ по Математике 5 класс: Зубарева, Мордкович

Издатель: И.И. Зубарева, А.Г. Мордкович. 2013-2019г.

Сообщить об ошибке

Выберите тип ошибки:

Решено неверно

Опечатка

Плохое качество картинки

Опишите подробнее
в каком месте ошибка

Ваше сообщение отправлено
и скоро будет рассмотрено

ОК, СПАСИБО

[email protected]

© OTVETKIN.INFO

Классы

Предметы

Номер 457 — ГДЗ по Математике 5 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2021.

Часть 2 (решебник)Номер 457 — ГДЗ по Математике 5 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2021. Часть 2 (решебник) — GDZwow

Перейти к содержанию

Search for:

Авторы: Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И.

Издательство: Мнемозина

Тип: Учебник

Новая версия

1 ЧАСТЬ

Выберите номер

123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310312313314315316317318319320321322323324325326327328329330331332333334335336337338339340341342343344345346347348349350351352353354355356357358359360361362363364365366367368369370371372373374375376377378379380381382383384385386387388389390391392393394395396397398399400401402403404405406407408409410411412413414415416417418419420421422423424425426427428429430432433434435436437438439440441442443444445446447448449450451452453454455456457458459460461462463464465466467468469470471472473474475476477478479480481482483484485486487488489490491492493494495496497498499500501502503504505506507508509510511512513514515516517518519520521522523524525526527528529530531532533534535536537538539540541542543544545546547548549550551552553554555556557558559560561562563564565566567568569570571572573574575576577578579580581582583584585586587588589590591592593594595596597598599600601602603604605606607608609610611612613614615616617618619620621622623624625626627628629630631632633634635636637638639640641642643644645646647648649650651652653654655656657658659660661662663664665666667668669670671672673674675676677678679680681682683684686687688689690691692693694695696697698698699701702703704705706707708709710711712713714715716717718719720721722723724725726727728729730731732733734735736737738739740741742743744745746747748749750751752753754755756757758759760761762763764765766767768769770771772773774775776777778779780781782783784785786787788789790791792793793794795797798799800801802803804805806807808809810811812813814815816817817819820821822823824825826827828829830831832833834835836837838839840841842843844845846847848849850851852

2 ЧАСТЬ

Выберите номер

12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394959697989910010110210310410510610710810911011111211311411511611711811912012112212312412512612712812913013113213313413513613713813914014114214314414514614714814915015115215315415515615715815916016116216316416516616716816917017117217317417517617717817918018118218318418518618718818919019119219319419519619719819920020120220320420520620720820921021121221321421521621721821922022122222322422522622722822923023123223323423523623723823924024124224324424524624724824925025125225325425525625725825926026126226326426526626726826927027127227327427527627727827928028128228328428528628728828929029129229329429529629729829930030130230330430530630730830931031131231331431531631731831932032132232332432532632732832933033133233333433533633733833934034134234334434534634734834935035135235335435535635735835936036136236336436536636736836937037137237337437537637737837938038138238338438538638738838939039139239339439539639739839940040140240340440540640740840941041141241341441541641741841942042142242342442542642742842943043143243343443543643743843944044144244344444544644744845045145245345445545645745845946046146246346446546646746846947047147247347447547647747847948048148248348448548648748848949049149249349449549649749849950050150250350450550650750850951051151251351451551651751851952052152252352452552652752852953053153253353453553653753853954054154254354454554654754854955055155255355455555655755855956056156256356456556656756856957057157257357457557657757857958058158258358458558658758858959059159259359459559659759859960060160260360460560660760860961061161261361461561661761861962062162262362462562662762862963063163263363463563663763863964064164264364464564664764864965065165465565665765865966066166266366466566666766866967067167267367467567667767867968068168268368468568668768868969069169269369469569669769869970070170270370470570670770870971071171271371471571671771871972072172272372472572672772872973073173273373473573673773873974074174274374474574674774874975075175275375475575675775875976076176276376476576676776876977077177277377477577677777877978078178278378478578678778878979079179279379479579679779879980080180280380480580680780880981081181281381481581681781881982082182282382482582682782882983083183283383483583683783883984084184284384484584684784884985085185285385485585685785885986086186286386486586686786886987087187287387487587687787887988088188288388488588688788888989089189289389489589689789889990090190290390490590690790890991091191291391491591691791891992092192292392492592692792892993093193293393493593693793893994094194294394494594694794894995095195295395495595695795895996096196296396496596696796896997097197297397497597697797897998098198298398498598698798898999099199299399499599699799899910001001100210031004100510061007100810091010101110121013101410151016101710181019102010211022102310241025102610271028102910301031103210331034103510361037103810391040104110421043104410451046104710481049105010511052105310541055105610571058105910601061106210631064106510661067106810691070107110721073107410751076107710781079108010811082108310841085108610871088108910901091109210931094109510961097109810991100110111021103110411051106110711081109111011111112111311141115111611171118111911201121112211231124112511261127112811291130113111321133113411351136113711381139114011411142114311441145114611471148114911501151115211531154115511561157115811591160116111621163116411651166116711681169117011711172117311741175117611771178117911801181118211831184118511861187118811891190119111921193119511961197119811991200120112021203120412051206120712081209121012111212121312141215121612171218121912201221122212231224122512261227122812291230123112321233123412351236123712381239124012411242124312441245124612471248124912501251125212531254125512561257125812591260126112621263126412651266126712681269127012711272127312741275127612771278127912801281128212831284128512861287128812891290129112921293129412951296129712981299130013011302130313041305130613071308130913101311131213131314131513161317131813191320132113221323132413251326132713281329133013311332133313341335133613371338133913401341134213431344134513461347134813491350135113521353135413551356135713581359136013611362136313641365136613671368136913701371137213731374137513761377137813791380138113821383138413851386138713881389139013911392139313941395139613971398139914001401140214031404140514061407140814091410141114121413141414151416141714181419142014211422142314241425142614271428142914301431143214331434143514361437143814391440144114421443144414451446144714481449145014511452145314541455145614571458145914601461146214631464146514661467146814691470147114721473147414751476147714781479148014811482148314841485148614871488148914901491149214931494149514961497149814991500150115021503150415051506150715081509151015111512151315141515151615171518151915201521152215231524152515261527152815291530153115321533153415351536153715381539154015411542154315441545154615471548154915501551155215531554155515561557155815591560156115621563156415651566156715681569157015711572157315741575157615771578157915801581158215831584158515861587158815891590159115921593159415951596159715981599160016011602160316041605160616071608160916101611161216131614161516161617161816191620162116221623162416251626162716281629163016311632163316341635163616371638163916401641164216431644164516461647164816491650165116521653165416551656165716581659166016611662166316641665166616671668166916701671167216731674167516761677167816791680168116821683168416851686168716881689169016911692169316941695169616971698169917001701170217031704170517061707170817091710171117121713171417151716171717181719172017211722172317241725172617271728172917301731173217331734173517361737173817391740174117421743174417451746174717481749175017511752175317541756175717581759176017611762176317641765176617671768176917701771177217731774177517761777177817791780178117821783178417851786178717881789179017911792179317941795179617971798179918001801180218031804180518061807180818091810181118121813181418151816181718181819182018211822182318241825182618271828182918301831183218331834183518361837183818391840184118421843184418451846184718481849

Adblock
detector

Обратная задача рассеяния для уравнений Максвелла вне движущегося тела

Владимир Георгиев

    Annales de l’I.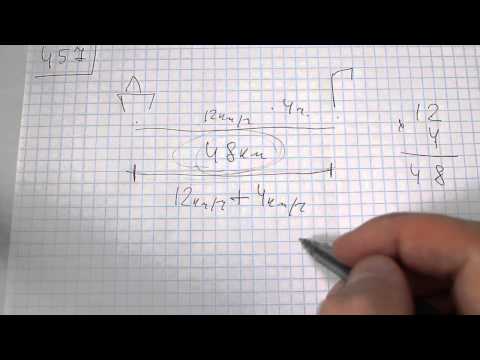 H.P. Теоретическое телосложение (1989)

    • Том: 50, Выпуск: 1, стр. 37-70
    • ISSN: 0246-0211

    Доступ к полной статье

    топ

     Доступ к полному тексту

     Полный (PDF)

    Как цитировать

    топ
    • MLA
    • БибТекс
    • РИС

    Георгиев Владимир. «Обратная задача рассеяния для уравнений Максвелла вне движущегося тела». Анналы I.H.P. Теоретическое телосложение 50.1 (1989): 37-70. .

    @статья{Georgiev1989,
    автор = {Георгиев, Владимир}, 9Журнал 0032 = {Annales de l’I.H.P. Physique théorique},
    ключевых слова = {рассеивание; акустические волны; движущиеся препятствия; ведущая сингулярность; ядро рассеяния; уравнения Максвелла; микролокальная параметрикс},
    язык = {анг},
    номер = {1},
    страницы = {37-70},
    издатель = {Готье-Вилларс},
    заголовок = {обратная задача рассеяния для уравнений Максвелла снаружи движущееся тело},

    url = {http://eudml. org/doc/76435},
    том = {50},
    год = {1989},
    }

    TY — JOUR
    AU — Георгиев, Владимир
    TI — Обратная задача рассеяния для уравнений Максвелла вне движущегося тела
    JO — Annales de l’I.H.P. Physique théorique
    PY — 1989
    PB — Gauthier-Villars
    VL — 50
    IS — 1
    SP — 37
    EP — 70
    LA — eng
    KW — рассеяние; акустические волны; движущиеся препятствия; ведущая сингулярность; ядро рассеяния; уравнения Максвелла; микролокальный параметрикс
    UR — http://eudml.org/doc/76435
    ER —

    Ссылки

    top
    1. [1] A. Bachelot et V. Petkov, Existence de l’opérateur de диффузия pour l’equation des ondes avec un potentiel périodique en temps, C. R. Acad. науч. Париж, Серия I, t. 303, 1986, с. 671-673. Збл0611.35067МР870693
    2. [2] А. Бачело и В. Петков, Opérateurs d’ondes pour les systemes hyperboliques avec un potentiel périodique en temps, Ann. Инст. Анри Пуанкаре, Physique Théorique, t. 47, 1987, с. 383-428. Збл0657.35102МР933684
    3. [3] Дж. Купер и В. Штраус, Энергетическая связанность и локальный энергетический распад волн, отражающихся от движущегося препятствия, Индиана Юнив. Мат. Дж., т. 25, 1976, с. 671-690. Збл0348.35059МР415093
    4. [4] Дж. Купер и В. Штраус, Представление оператора рассеяния для движущихся препятствий, Индиана Univ. Мат. Дж., т. 28, 1979, с. 643-671. Збл0427.35056МР542950
    5. [5] Дж. Купер, В. Штраус, Рассеяние волн периодически движущимися телами, J. Funct. Анал., т. 1, с. 47, 1982, с. 180-229. Збл0494.35073МР664336
    6. [6] J. Cooper и W. Strauss, Абстрактная теория рассеяния для периодических во времени систем с приложениями к электромагнетизму, Indiana Univ. Мат. Дж., т. 34, 1985, с. 33-83. Збл0582.47011МР773393
    7. [7] Купер Дж. , Штраус В. Ведущая особенность волны, отраженной движущейся границей, Дифф. экв., т. ед. 52, 1984, с. 175-203. Збл0547.35075МР741267
    8. [8] Дж. Купер и В. Штраус, Начально-краевая задача для уравнений Максвелла в присутствии движущегося тела, SIAM, Journal Math. Анал., т. 1, с. 16, 1985, с. 1165- 1179. Zbl0593.35069MR807903
    9. [9] Дж. Копер и В. Штраус, Неопубликованная рукопись, 1985. 
    10. [10] И. Гельфанд, М. Граев, Х. Виленкин, Интегральная геометрия и смежные вопросы теории представлений, М., 1962 (на русском языке).
    11. [11] S. Helgason, Преобразование Радона на евклидовых пространствах, компактных двухточечных однородных пространствах и многообразиях Грассмана, Acta Math., т. 1, с. 113, 1965, с. 153-180. Збл0163.16602МР172311
    12. [12] Л. Хёрмандер, Анализ линейных дифференциальных операторов в частных производных I, Теория распределения и анализ Фурье, Springer Verlag, Berlin-Heidelberg-New York-Toronto, 1983. Zbl0521.35001MR717035
    13. [13] H. Iwashita, Спектральная теория для симметричных систем во внешней области, препринт, появится в Tsukuba, J. Math. Збл0655.35059МР926454
    14. [14] Х. Ивасита, Спектральная теория для симметричных систем во внешней области. II. Часть, препринт. Збл0669.47003MR976314
    15. [15] Т. Като, Линейные эволюционные уравнения «гиперболического» типа, J. ​​Fac. науч. ун-т Токио, т. 17, 1970, с. 241-258. Збл0222.47011МР279626
    16. [16] П. Лакс и Р. Филлипс, Теория рассеяния, Academic Press, Нью-Йорк, 1967. Zbl0186.16301MR217440
    17. [17] П. Лакс и Р. Филлипс, Локальные граничные условия для диссипативных симметричных линейных дифференциальных операторов, Comm. Чистое приложение Матем., т. 1, с. 13, 1960, с. 427-455. Збл0094.07502МР118949
    18. [18] А. Майда, С. Ошер, Начально-краевые задачи для гиперболических уравнений с равномерно характеристической границей, Комм. Чистое приложение Матем., т. 1, с. 28, 1975, с. 607-675. Збл0314.35061МР410107
    19. [19] А. Майда, Формула представления оператора рассеяния и обратная задача для произвольных тел, Комм. Чистое приложение Матем., т. 1, с. 30, 1977, с. 165-194. Збл0335.35076МР435625
    20. [20] A. Majda и M. Taylor, Обратные задачи рассеяния для прозрачных препятствий, электромагнитных волн и гиперболических систем, Comm. Часть. Дифф. экв., т. ед. 2, 1977, с. 395-438. Збл0373.35055МР437946
    21. [21] Р. Мелроуз, Рассеяние вперед на выпуклом препятствии, Comm. Чистое приложение Матем., т. 1, с. 33, 1980, с. 461-499. Збл0435.35066МР575734
    22. [22] Р. Мелроуз, Сингулярности и затухание энергии при акустическом рассеянии, Duke Math. Дж., т. 46, 1979, с. 43-59. Збл0415. 35050МР523601
    23. [23] В. Петков, Представление оператора рассеяния для диссипативных гиперболических систем, Комм. ПДЭ, т.к. 6, 1981, с. 993-1022. Збл0464.35070МР627656
    24. [24] В. Петков, Теория рассеяния для гиперболических операторов, Notas de Curso, № 24, Departemento de Matematica, Universidade Federal de Pernambuco, Recife, 1987. MR912265
    25. [25] В. Петков и Ц. Рангелов, Ведущая особенность ядра рассеяния, Comp. Ренд. акад. науч. булг., т. н. 40, № 12, 1987, с. 5-8. Збл0657.35106МР937109
    26. [26] Дж. Раух, Ф. Мэсси, Дифференцируемость решений гиперболических начально-краевых задач, Тр. амер. Мат. Соц., т. 1, с. 189, 1974, с. 303-318. Збл0282.35014МР340832
    27. [27] Дж. Раух, Симметричные положительные системы с граничной характеристикой постоянной кратности, Тр. амер. Мат. Соц., т. 1, с. 291, 1985, с. 167-187. Збл0549.35099МР797053
    28. [28] Г. Шмидт, Спектральная теория и теория рассеяния для уравнений Максвелла во внешней области, Arch. Крыса. мех. Анал., т. 1, с. 28, 1975, с. 284-322. Збл0155.43502
    29. [29] H. Soga, Особенности ядра рассеяния для выпуклых препятствий, J. Math. Киотский ун-т, ул. 22, 1983, с. 729-765. Збл0511.35070МР685528 ​​
    30. [30] М. Тейлор, Псевдодифференциальные операторы, Издательство Принстонского университета, Принстон, Нью-Джерси, 1981. Zbl0453.47026MR618463
      31. .
    31. [31] М. Тейлор, Отражение особенностей решений систем дифференциальных уравнений, CPAM, т. 1, с. 27, 1975, с. 457-478. Збл0332.35058МР509098
    32. [32] Р. Утиама, Теория относительности, Иванами, 1977 (в Японии).
    33. [33] J. Van Bladel, Электромагнитные поля в присутствии тел вращения, Proc. IEEE, т. 1, с. 64, 1976, с. 301-318.

    Цитаты в документах EuDML

    top
    1. В. Петков, Обратные задачи диффузии для возмущений, зависящих от температуры
    top

    Вы должны войти, чтобы оставлять комментарии.

    Об ограниченности L1-нормы ядер Уолша–Фейера

    • title={Об ограниченности L1-нормы ядер Уолша–Фея}, автор={Родольфо Толедо}, journal={Журнал математического анализа и приложений}, год = {2018}, объем={457}, страницы = {153-178} }
      • R. Toledo
      • Опубликовано 2018
      • Математика
      • Журнал математического анализа и применений

      Взгляд через издатель

      doi.org

      Максимальные операторы Walsh-N \ «Orlund Mine On Dyadic Hardy

      4
      • Ю. Гогинава

      • Математика

      • 2022

      В представленной работе доказываются необходимые и достаточные условия для того, чтобы максимальный оператор средних Уолша-Нёрлунда с невозрастающими весами был ограничен из диадического пространства Харди (Я)…

      Средние Чезаро с переменными параметрами рядов Уолша–Фурье

      В этой статье обсуждаются некоторые свойства сходимости и расходимости подпоследовательностей средних Чезаро с переменными параметрами рядов Уолша–Фурье. Приводятся необходимые и достаточные условия для…

      Сходимость и расходимость почти всюду чезаровских средних при меняющихся параметрах рядов Уолша–Фурье ряда Уолша–Фурье.

      Матричная суммируемость Walsh -Fourier Series

      • U. Goginava, K. Nagy

      • Математика

        Математика

      • 2022

      Представленная статья. В частности, мы обсуждаем сходимость матричных преобразований в пространстве L1 и в пространстве CW в терминах модуля…0164

      В этой статье мы обсуждаем поведение Θ-средних рядов Уолша — Фурье функции в диадических пространствах Харди Hp и диадических однородных банаховых пространствах X. А именно, мы оцениваем скорость…

      Сопряженных преобразований на диадической группе

      Abstract В работе исследуются свойства константы Лебега сопряженных преобразований. Для сопряженных средних Фейера мы найдем необходимое и достаточное условие на $$t$$, для которого…

      Сопряженные преобразования на диадической группе

      В этой статье мы изучаем свойства константы Лебега сопряженных преобразований. Для сопряженных средних Фейера найдем необходимое и достаточное условие на \documentclass[12pt]{минимальное}… ограниченная вариация

      • Ю. Малыхин, С. А. Теляковский, Н. Холщевникова

      • Математика

      • 2015

      Устанавливаем необходимые и достаточные условия на последовательность, разбивающую ряды Фурье–Уолша на блоки, при которых ряд, состоящий из модулей таких блоков ряда…

      Лебеговы константы системы Уолша и банаховы пределы

      • С. Асташкин, Е. М. Семенов

      • Математика

      • 2016

      Изучены свойства констант Лебега системы Уолша Ln(W), n ∈ N, и применены результаты к теории банаховых пределов . Покажем, что последовательность $$\left\{ {\frac{{{L_n}\left( W…

      Walsh Series, An Introduction to Dyadic Harmonic Analysis

      • F. Schipp, W. R. Wade, P. Simon

      • Mathematics

      • 1990

      Introduction Walsh-Fourier coefficients dyadic martingales and Hardy spaces convergence in norm approximation and базисы почти всюду сходимость и суммируемость рядов Уолша-Фурье…

      О суммируемости (C,1) для систем типа Виленкина

      • Г.

        No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *