Математика 5 класс виленкин 453: Номер №453, Часть 2 — ГДЗ по Математике 5 класс: Виленкин Н.Я.

Содержание

Номер №453 — ГДЗ по Математике 5 класс: Виленкин Н.Я.

войтирегистрация

Ответкин
Решебники
5 класс
Математика
Виленкин
Номер №453

НАЗАД К СОДЕРЖАНИЮ

2013г.ВыбранВыбрать ГДЗ (готовое домашние задание из решебника) на Номер №453 по учебнику Математика. 5 класс : учебник для учащихся общеобразовательных учреждений / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 31 издание 2013г.

2019г.ВыбранВыбрать ГДЗ (готовое домашние задание из решебника) на Номер №453 по учебнику Математика. 5 класс : учебник для учащихся общеобразовательных организаций / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 37 издание 2019г.

Условие 20132019г.

Cменить на 2013 г.

Cменить на 2019 г.

В треугольнике ABC сторона АВ равна 27 см, и она больше стороны ВС в 3 раза. Найдите длину стороны АС, если периметр треугольника ABC равен 61 см.

Решение 1

Решение 2

Решение 3

ГДЗ по Математике 5 класс: Виленкин Н.Я.

Издатель: Виленкин Н.Я. Жохов В.И. Чесноков А.С. Шварцбурд С.И. 2013/2019г.

ГДЗ по Математике 5 класс: Мерзляк А. Г.

Издатель: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. 2014-2018г.

ГДЗ по Математике 5 класс: Никольский С.М.

Издатель: С.М. Никольский, М.К, Потапов, Н.Н. Решетников А.В. Шевкин. 2015-2021г

ГДЗ по Математике 5 класс: Дорофеев Г.В.

Издатель: Г.В. Дорофеев, И.Ф. Шарыгин, С.Б. Суворова. 2017-2019г.

ГДЗ по Математике 5 класс: Зубарева, Мордкович

Издатель: И.И. Зубарева, А.Г. Мордкович. 2013-2019г.

Сообщить об ошибке

Выберите тип ошибки:

Решено неверно

Опечатка

Плохое качество картинки

Опишите подробнее
в каком месте ошибка

Ваше сообщение отправлено
и скоро будет рассмотрено

ОК, СПАСИБО

[email protected]

Классы

Предметы

Номер 453 — ГДЗ по Математике 5 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2021.

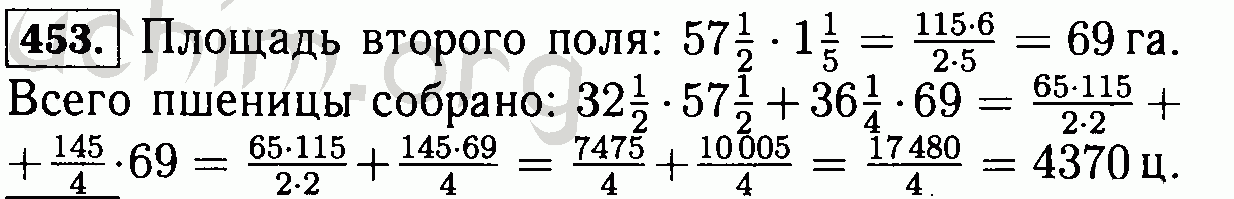Часть 1 (решебник)Номер 453 — ГДЗ по Математике 5 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2021. Часть 1 (решебник) — GDZwow

Перейти к содержанию

Search for:

Авторы: Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И.

Издательство: Мнемозина

Тип: Учебник

Новая/Старая версия

1 ЧАСТЬ

Выберите номер

2 ЧАСТЬ

Выберите номер

12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394959697989910010110210310410510610710810911011111211311411511611711811912012112212312412512612712812913013113213313413513613713813914014114214314414514614714814915015115215315415515615715815916016116216316416516616716816917017117217317417517617717817918018118218318418518618718818919019119219319419519619719819920020120220320420520620720820921021121221321421521621721821922022122222322422522622722822923023123223323423523623723823924024124224324424524624724824925025125225325425525625725825926026126226326426526626726826927027127227327427527627727827928028128228328428528628728828929029129229329429529629729829930030130230330430530630730830931031131231331431531631731831932032132232332432532632732832933033133233333433533633733833934034134234334434534634734834935035135235335435535635735835936036136236336436536636736836937037137237337437537637737837938038138238338438538638738838939039139239339439539639739839940040140240340440540640740840941041141241341441541641741841942042142242342442542642742842943043143243343443543643743843944044144244344444544644744845045145245345445545645745845946046146246346446546646746846947047147247347447547647747847948048148248348448548648748848949049149249349449549649749849950050150250350450550650750850951051151251351451551651751851952052152252352452552652752852953053153253353453553653753853954054154254354454554654754854955055155255355455555655755855956056156256356456556656756856957057157257357457557657757857958058158258358458558658758858959059159259359459559659759859960060160260360460560660760860961061161261361461561661761861962062162262362462562662762862963063163263363463563663763863964064164264364464564664764864965065165465565665765865966066166266366466566666766866967067167267367467567667767867968068168268368468568668768868969069169269369469569669769869970070170270370470570670770870971071171271371471571671771871972072172272372472572672772872973073173273373473573673773873974074174274374474574674774874975075175275375475575675775875976076176276376476576676776876977077177277377477577677777877978078178278378478578678778878979079179279379479579679779879980080180280380480580680780880981081181281381481581681781881982082182282382482582682782882983083183283383483583683783883984084184284384484584684784884985085185285385485585685785885986086186286386486586686786886987087187287387487587687787887988088188288388488588688788888989089189289389489589689789889990090190290390490590690790890991091191291391491591691791891992092192292392492592692792892993093193293393493593693793893994094194294394494594694794894995095195295395495595695795895996096196296396496596696796896997097197297397497597697797897998098198298398498598698798898999099199299399499599699799899910001001100210031004100510061007100810091010101110121013101410151016101710181019102010211022102310241025102610271028102910301031103210331034103510361037103810391040104110421043104410451046104710481049105010511052105310541055105610571058105910601061106210631064106510661067106810691070107110721073107410751076107710781079108010811082108310841085108610871088108910901091109210931094109510961097109810991100110111021103110411051106110711081109111011111112111311141115111611171118111911201121112211231124112511261127112811291130113111321133113411351136113711381139114011411142114311441145114611471148114911501151115211531154115511561157115811591160116111621163116411651166116711681169117011711172117311741175117611771178117911801181118211831184118511861187118811891190119111921193119511961197119811991200120112021203120412051206120712081209121012111212121312141215121612171218121912201221122212231224122512261227122812291230123112321233123412351236123712381239124012411242124312441245124612471248124912501251125212531254125512561257125812591260126112621263126412651266126712681269127012711272127312741275127612771278127912801281128212831284128512861287128812891290129112921293129412951296129712981299130013011302130313041305130613071308130913101311131213131314131513161317131813191320132113221323132413251326132713281329133013311332133313341335133613371338133913401341134213431344134513461347134813491350135113521353135413551356135713581359136013611362136313641365136613671368136913701371137213731374137513761377137813791380138113821383138413851386138713881389139013911392139313941395139613971398139914001401140214031404140514061407140814091410141114121413141414151416141714181419142014211422142314241425142614271428142914301431143214331434143514361437143814391440144114421443144414451446144714481449145014511452145314541455145614571458145914601461146214631464146514661467146814691470147114721473147414751476147714781479148014811482148314841485148614871488148914901491149214931494149514961497149814991500150115021503150415051506150715081509151015111512151315141515151615171518151915201521152215231524152515261527152815291530153115321533153415351536153715381539154015411542154315441545154615471548154915501551155215531554155515561557155815591560156115621563156415651566156715681569157015711572157315741575157615771578157915801581158215831584158515861587158815891590159115921593159415951596159715981599160016011602160316041605160616071608160916101611161216131614161516161617161816191620162116221623162416251626162716281629163016311632163316341635163616371638163916401641164216431644164516461647164816491650165116521653165416551656165716581659166016611662166316641665166616671668166916701671167216731674167516761677167816791680168116821683168416851686168716881689169016911692169316941695169616971698169917001701170217031704170517061707170817091710171117121713171417151716171717181719172017211722172317241725172617271728172917301731173217331734173517361737173817391740174117421743174417451746174717481749175017511752175317541756175717581759176017611762176317641765176617671768176917701771177217731774177517761777177817791780178117821783178417851786178717881789179017911792179317941795179617971798179918001801180218031804180518061807180818091810181118121813181418151816181718181819182018211822182318241825182618271828182918301831183218331834183518361837183818391840184118421843184418451846184718481849

Adblock
detector

Эквивалентность прямого квантования и квантования Уилера-ДеВитта – arXiv Vanity

Abstract

Обосновываем способ прямого квантования, что означает непосредственное квантование закона сохранения. Показано, что такой подход эквивалентен введению супер гамильтониан на минисуперпространстве в духе подхода Уилера-ДеВитта. Тогда у нас будет: все значения наблюдаемы и имеют очевидный физический смысл и четко определенный домен приложения; волновая функция хорошо определена без квантования времени и часто может быть точно получено; мы можем решить основные математические проблемы, и поэтому более сложные модели можно рассматривать точно без теории возмущений.

gr-qc/9709030

Теория тонких оболочек в ОТО:

Эквивалентность прямого квантования и квантования Уилера-ДеВитта

Злощастьев Константин Григорьевич

Кафедра теоретической физики, Днепропетровский государственный университет,

, Научный пер., 13, Днепропетровск, 320625, Украина.

PACS номера: 04.60.Kz, 11.17.+г

Ключевые слова: тонкая оболочка, квантовая гравитация, модель минисуперпространства.

Адрес для жесткой корреспонденции:
К. Г. Злощатьев

Метростроевская 5, кв.453
Днепропетровск 320128
Украина

Электронная почта:

Начиная с классических произведений [1, 2] исследование тонких оболочек в ОТО получила большое развитие (см. обзоры [3]). В настоящей статье мы рассмотрим общий класс сферически симметричные оболочки с ненулевым поверхностным натяжением [4] тем самым основной внимание будет уделено квантовым аспектам теории.

Рассмотрим тонкий слой с поверхностным тензором энергии-импульса идеальная жидкость в общем случае (мы используем единицы γ=c=1, где γ — гравитационная постоянная)

Sab=σuaub+p(uaub+ (3)gab),

(1)

где σ и p — поверхностная плотность энергии и давление соответственно, ua – времяподобный единичный вектор, (3)gab — метрика оболочки.

Запишем метрику пространства-времени вне Σout и внутри Σ в сферической оболочке в виде

ds2(outin)=−Φ±(r)dt2±+Φ±(r)−1dr2+r2dΩ2,

(2)

где dΩ2 — метрика единичной 2-сферы. Можно показать, что если использовать собственное время τ оболочки, тогда закон сохранения энергии можно записать как

d (σ√(3)g)=−p d(√(3)g)−√(3)g [(Tτn)выход–(Tτn)вход]dτ,

(3)

где Tτn=Tαβuαnβ — проекция тензоров энергии-импульса в пространстве-времени Σout и Σin на касательном и нормальном векторах, (3)g=det((3)gab). Метрика оболочки на мировом листе равна 9.0005

(3)ds2=-dτ2+R2dΩ2,

(4)

где R(τ) оказывается собственным радиусом оболочки.

Наложение условий соединения через оболочку, выведем уравнения движения таких оболочек в виде

	ϵ+√˙R2+Φ+(R)−ϵ−√˙R2+Φ−(R)=−mR,		(5)
	м=4πσ(R)R2,

где ˙R=dR/dτ, m — (эффективная) масса покоя. Выбор пары {ϵ+=±1, ε−=±1} делит все оболочки на классы типа черной дыры (ЧД) и проходимые оболочки типа червоточины (WH). Уравнения (3) и (5) вместе с состоянием уравнение p=p(σ,(3)g) и выбор знаков ϵ± однозначно определяют движение жидкой оболочки. В дальнейшем будем считать σ(R) уже известная функция теории, поскольку в большинстве случаев мы можем разрешить сохранение закон (3) независимо от уравнения движения [5] . Уравнение (5) можно переписать и без корней: double возводя в квадрат получаем

˙R2=[ΔΦ−m2/R22m/R]2−Φ−(R),

(6)

где ΔΦ=Φ+(R)−Φ−(R).

В настоящее время существует множество подходов к квантованию тонких оболочки, связанные с различными способ построения гамильтониана структура [6, 7, 8, 9] . Конечно, (почти) все эти методы дают разные результаты. (волновые функции, спектры и т. д.), таким образом, мы можем наблюдать неэквивалентные теории во всем их обескураживающем многообразии. Поэтому необходимо выработать какой-то единый подход с помощью что мы могли бы сравнить модели. Кроме того, многие известные подходы используют теорию возмущений для получить окончательные результаты, которые могут быть опасны в рамках сильно нелинейная общая теория относительности. Таким образом, было бы очень важно, чтобы этот единый подход также будет максимально непертурбативным.

Чистый минисуперпространственный подход, не требующий времени нарезка и шкала времени кажется наиболее подходящей кандидат (см., например, Ref. [10] ). Действительно, если взглянуть на уравнение (6), можно не видеть время как переменная. Кроме того, дифференциальные уравнения второго порядка, из которых уравнение (6) был полученные, также не содержат переменной времени [2] . Поэтому, в чем причина введения времени (и связанных с ним понятий) насильно, тем более, что это создает дополнительные хлопоты? Рассмотрим оба подхода в рамках Метод минисуперпространства.

(a) Заход на посадку с эффективной массой
Сначала рассмотрим модель минисуперпространства описывается лагранжианом

L=m˙R22−m2⎧⎨⎩Φ−−[ΔΦ−m2/R22m/R]2⎫⎬⎭,

(7)

где мы означают интеграл как первообраз, m – указанное выше эффективная масса покоя, m=m(R).

Таким образом, уравнение движения

ddτ(m˙R)=m,R˙R22−12⎧⎨⎩mΦ−−m[∆Φ−m2/R22m/R]2⎫⎬⎭,R,

где «,R» означает производную относительно R.

Используя временную симметрию, мы можем легко уменьшить порядок этого дифференциальное уравнение и получать уравнение (6) до аддитивной константы, которая может быть откалибрована к нулю (обратите внимание, что он равен нулю только на траекториях, поэтому ограничение). Поэтому наш лагранжиан действительно описывает динамику тонких оболочек. Момент, сопряженный переменной R, равен Π=m˙R, и (супер)гамильтониан

H=Π22m+m2⎧⎨⎩Φ−−[ΔΦ−m2/R22m/R]2⎫⎬⎭.

(8)

Приставка «супер» означает, что, строго говоря, H является функционалом определенный на суперпространстве, которое является пространством всех 3-метрик мирового листа (4) и конфигурации поля материи, действующие на оболочку.

Только из-за сферической симметрии и наличия одиночного нераспространяющегося степени свободы мы можем получить его как стандартный гамильтониан.

Вспоминая упомянутую выше нулевую константу, получаем, что H=0 на траекториях (6). Таким образом, мы имеем в виду этот (супер)гамильтониан как ограничение, т. е.

Н≈0,

(9)

или, в квантовом случае (Π=−i∂R)

НΨ≈0,

(10)

и может напрямую квантовать уравнение. (6) без каких-либо предположений о времени, как это было сделано в особом случае m=const (пылевая оболочка, σ=m/4πR2) в исх. [11]

. Следовательно, всегда можно проквантовать уравнение. (6) напрямую без лишних мотиваций про шкалу времени и т.п., просто замените ˙R2 на Π2/м2.

Тогда в планковских единицах получаем волновое уравнение для волновой функции Уилера-ДеВитта Ψ(R):

Ψ′′+m2⎧⎨⎩[ΔΦ−m2/R22m/R]2−Φ−⎫⎬⎭Ψ=0,

(11)

от которые (для связанных состояний, если они существуют) мы можем получить спектры для необходимые значения, например, полная масса-энергия M+ [12] и т. д.

Однако следует отметить, что существует еще один лагранжиан.

(b) Подход с планковской массой
Рассмотрим модель минисуперпространства, описываемую лагранжианом

L=mpl˙R22-mpl2⎧⎨⎩Φ—[ΔΦ-m2/R22m/R]2⎫⎬⎭.

(12)

Там же образом, как было указано выше, можно видеть, что соответствующее уравнение движения дает уравнение. (6). Момент, сопряженный переменной R, равен Π=mpl˙R а (супер)гамильтониан равен

H=Π22mpl+mpl2⎧⎨⎩Φ−−[ΔΦ−m2/R22m/R]2⎫⎬⎭.

(13)

Легко видеть, что уравнения. (9), (10) справедливы. Следовательно, можно квантовать уравнение (6) напрямую путем замены ˙R2 на Π2/m2pl. Таким образом, в планковских единицах мы получаем волновое уравнение для Волновая функция Уилера-ДеВитта Ψ(R):

Ψ′′+⎧⎨⎩[ΔΦ−m2/R22m/R]2−Φ−⎫⎬⎭Ψ=0.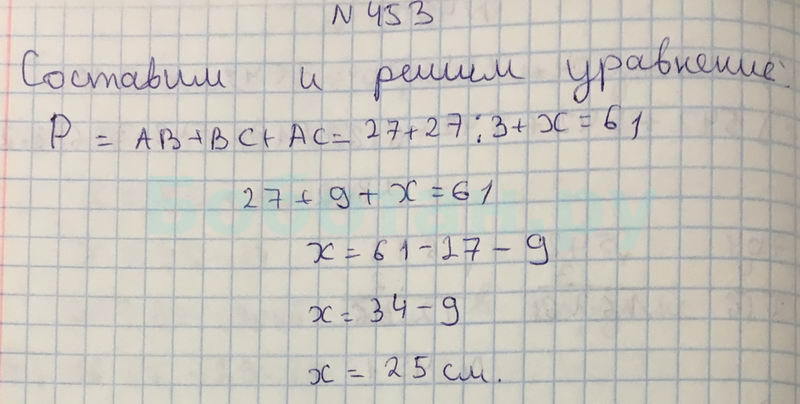

(14)

Сравнение уравнения (11) и (14), мы видим, что они не одинаковы и в общем случае приводят к разным результатам; однако мы не можем отдать абсолютного предпочтения ни одному из них. Более того, наши лагранжианы всегда определены с точностью до некоторого произвольного мультипликативная функция R, которая не влияет на уравнение движения (6), но обязательно появляется в гамильтонианах. Произвол этой функции есть не что иное, как произвол выбор подходящего калибра.

Наконец, следует указать, как топология червоточины/черной дыры следует учитывать при квантовании. Действительно из уравнений. (6), (8), (13) очевидно, что по двойной квадрат мы аннигилировали корневые знаки ϵ, определяющие топологию. Однако при квантовании мы всегда можем учитывать топологию, потому что уравнения (11), (14) следует дополнить граничные условия (например, в нуле и пространственной бесконечности), которые, очевидно, определяется специфическая (червоточина или черная дыра) топология.

Таким образом, в настоящей статье мы разработали минисуперпространство подход и выполнен непертурбативный канонический квантование сферически симметричные сингулярные гиперповерхности в общей теории относительности.

[1] Г. Докур, Матем. Нахр. 27 (1964) 277.
[2] З. Израиль, Нуово Чименто Б 44 (1966) 1.
[3] Х.Сато, прог. Теор. физ. 76 (1986) 1250;
К. Маэда, Генерал Относительный. Гравит. 18 (1986) 931.
[4] К.В.Кухарж, Чехия. Дж. Физ. Б 18 (1968) 435.
[5] КГ. Злощатьев, Мод. физ. лат. А 13 (1998) 1419.
[6] К. Накамура, Ю. Осиро и А. Томимацу, физ. Ред. D 54 (1996) 4356.
[7] П. Гайичек и Й. Бичак, физ. ред. D 56 (1997) 4706; Дж. Л. Фридман, Дж. Луко и С. Н. Винтерс-Хилт, физ. Ред. D 56 (1997) 7674.
[8] В.А. Березин, Н.Г. Козимиров, В.А. Кузьмин, И.И. Ткачев, физ. лат. В 212 (1988) 415; В.А. Березин, физ. лат. В 241 (1990) 194; физ. Ред. Д 55 (1997) 2139; Нукл. физ. проц. Доп. 57 (1997) 181.
[9] П. Гайичек, Б.С. Кей и К.В. Кучарж, физ. Ред. D 46 (1992) 5439.
[10] А. Виленкин, Phys. Ред. D 50 (1994) 2581.
[11] КГ. Злощатьев, физ. Ред. D 57 (1998) 4812.
[12] М. Jaekel и S. Reynaud, Europhys. лат. 38 (1997) 1.

Преобразование Уолша класса булевых функций

Открытый доступ

Проблема		Уханьский унив. Дж. Нат. науч. Том 26, номер 6 , декабрь 2021


Страница (ы)		453 — 458
DOI		https://doi.org/10.1051/wujns/2021266453
Опубликовано онлайн		17 декабря 2021 г.

Карлет С, Меснагер С. Четыре десятилетия исследований изогнутых функций [J]. Проекты, коды и криптография, 2016, 78(1): 5-50. [Google Scholar]
Меснагер С. О полубент-функциях и связанных с ними плато-функциях над полем Галуа [M]. Берлин: Springer-Verlag, 2014. [Google Scholar]
TuZ B, ZhengD B, ZengX Y и др. Булевы функции с двумя различными коэффициентами Уолша [J]. Применимая алгебра в инженерных коммуникациях и вычислениях, 2011, 22 (5-6): 359-366. [Google Scholar]

Фрэнсис М, Литман А. О проблемах покрытия кодов [J]. Теория вычислительных систем, 1997, 30(2): 113-119.. [Перекрестная ссылка] [MathSciNet] [Google Scholar]
CalderbankR, KantorW M. Геометрия двухвесовых кодов [J]. Бюллетень Лондонского математического общества, 1986, 18 (2): 97-122. [Google Scholar]
КарлетК. Булевы функции для криптографии и коды исправления ошибок [J]. Энциклопедия математики и ее приложений, 2016, 78(1): 5-50. [Google Scholar]
Олсен Дж, Шольц Р, Уэлч Л. Последовательности бент-функций [J]. IEEE Transactions on Information Theory, 1982, 28(6): 858-864. [Перекрестная ссылка] [MathSciNet] [Google Scholar]
КарлетК. Булевы и векторные функции плато и функции APN [J]. IEEE Transactions on Information Theory, 2015, 61(11): 6272-6289. [Перекрестная ссылка] [MathSciNet] [Google Scholar]
SunZ Q, HuL. Булевы функции с четырехзначными спектрами Уолша [J]. Журнал системных наук и сложности, 2015, 28(3): 743-754. [Перекрестная ссылка] [MathSciNet] [Google Scholar]
JinW G, DuX N, SunY Z и др. Булевы функции с шестизначными спектрами Уолша и их применение [J]. Криптография и связь, 2021, 13(5): 393-405. [Google Scholar]
XuG K, CaoX W, XuS D. Несколько новых классов булевых функций с несколькими значениями преобразования Уолша [J]. Применимая алгебра в инженерных коммуникациях и вычислениях, 2017, 28 (2): 155-176. [Google Scholar]
TangC M, ZhouZ C, QiY F и др. Общая конструкция бент-функций и бент-идемпотентов с любыми возможными алгебраическими степенями [J]. IEEE Transactions on Information Theory, 2017, 63(10): 6149-6157. [Перекрестная ссылка] [MathSciNet] [Google Scholar]
Меснагер С. Несколько новых бесконечных семейств бент-функций и их двойственных [J]. IEEE Transactions on Information Theory, 2014, 60(7): 4397-4407. [Перекрестная ссылка] [MathSciNet] [Google Scholar]
PangT T, LiN, ZhangL и др.
No related posts.