Категории: 5 класс.

Математика 5 класс многоугольники равные фигуры: Конспект урока по теме Многоугольники. Равные фигуры 5 класс к учебнику А.Г. Мерзляк

 Комментировать

Содержание

стороны, вершины, диагонали. Периметр многоугольника

Многоугольник — это геометрическая фигура, ограниченная замкнутой ломаной линией, не имеющей самопересечений.

Звенья ломаной называются сторонами многоугольника, а её вершины — вершинами многоугольника.

Углами многоугольника называются внутренние углы, образованные соседними сторонами. Число углов многоугольника равно числу его вершин и сторон.

Многоугольникам даются названия по количеству сторон. Многоугольник с наименьшим количеством сторон называется треугольником, он имеет всего три стороны. Многоугольник с четырьмя сторонами называется четырёхугольником, с пятью — пятиугольником и т. д.

Обозначение многоугольника составляют из букв, стоящих при его вершинах, называя их по порядку (по часовой или против часовой стрелки). Например, говорят или пишут: пятиугольник  ABCDE:

В пятиугольнике 

ABCDE  точки  A,  B,  C,  D  и  E  — это вершины пятиугольника, а отрезки  AB,  BC,  CD,  DE  и  EA  — стороны пятиугольника.

Выпуклые и вогнутые

Многоугольник называется выпуклым, если ни одна из его сторон, продолженная до прямой линии, его не пересекает. В обратном случае многоугольник называется вогнутым:

Периметр

Сумма длин всех сторон многоугольника называется его периметром.

Периметр многоугольника  ABCDE  равен:

AB + BC + CD + DE + EA.

Если у многоугольника равны все стороны и все углы, то его называют правильным. Правильными многоугольниками могут быть только выпуклые многоугольники.

Диагональ

Диагональ многоугольника — это отрезок, соединяющий вершины двух углов, не имеющих общей стороны. Например, отрезок  AD  является диагональю:

Единственным многоугольником, который не имеет ни одной диагонали, является треугольник, так как в нём нет углов, не имеющих общих сторон.

Если из какой-нибудь вершины многоугольника провести все возможные диагонали, то они разделят многоугольник на треугольники:

Треугольников будет ровно на два меньше, чем сторон:

t = n — 2,

где  t  — это количество треугольников, а  n  — количество сторон.

Разделение многоугольника на треугольники с помощью диагоналей используется для нахождения площади многоугольника, так как чтобы найти площадь какого-нибудь многоугольника, нужно разбить его на треугольники, найти площадь этих треугольников и полученные результаты сложить

.

Равновеликие фигуры — свойства, формулы и примеры

Равные многоугольники

По определению равные фигуры должны быть во всём одинаковыми, включая площадь, длину сторон, размер углов и другие параметры. Чтобы рассмотреть всё из них, уйдёт много времени, да это и не нужно, ведь они взаимозависимы. Хорошим примером будет самый простой многоугольник — треугольник. Существует несколько правил, по которым можно определить, равны ли 2 треугольника между собой или нет:

  1. По трём сторонам.
  2. По стороне и двум прилегающим к ней углам.
  3. По двум сторонам и углу между ними.

Нельзя путать первое условие с тремя углами. Ведь если в треугольнике равны 3 угла, они необязательно будут равными, но будут подобными.

Названия условий достаточно точно описывают критерии, по которым можно определить одинаковые 2 треугольника или нет. Из них следует, что необязательно знать все параметры: часто хватает только нескольких из них для определения «равности».

В большинстве случаев определить одинаковость других фигур гораздо сложнее, нежели треугольников. К счастью, чаще всего в школьной геометрии такой класс задач не рассматривают или даются дополнительные данные, помогающие с решением.

Например, доказательство «равности» для четырёхугольника сложнее, да и почти не встречается. Но если по условию сказано, что четырёхугольник не произвольный, а имеет прямые углы, задача становится проще. В таком случае рассматривается прямоугольник. А для него достаточно, чтобы 2 не противолежащие стороны были равны.

Если указано ещё и условие, что прямоугольник является квадратом, достаточно указать, что у двух таких фигур совпадает по длине одна сторона и уже этого будет достаточно.

Равность правильных фигур

Частным и самым простым для сравнения является случай, когда многоугольник по условию правильный. Так называется фигура с одинаковыми сторонами и углами. Например, равносторонний треугольник и квадрат. Важно не забывать проверить равны ли углы, так как не каждая фигура правильная. Тот же ромб по определению имеет 4 совпадающие по длине стороны, но разные углы. При сравнении правильных многоугольников достаточно указать, что, хотя бы одна сторона фигуры равна стороне у другой. Это будет достаточное условие для доказательства «равности».

Самым простым и наглядным способом сверки двух фигур будет не геометрический с помощью правил, а путём наложения рисунков друг на друга. Разумеется, что он не претендует на точность, но изобразить параллелограмм и наложить его на другой нагляднее, чем сравнивать, например, углы. Понятно, что так можно только ознакомиться с концепцией «равности» и показать, какие фигуры называются равными, для упрощения в дальнейшем решения задач, но доказывать что-либо нельзя, ввиду неточности метода.

Если при сравнении двух тел оказывается, что их площади равны, такие тела (многоугольники) являются равновеликими. Как и в случае с прошлым, это определение звучит несложно. Проблемы могут начаться непосредственно при вычислении площадей. Самый простой многоугольник — треугольник.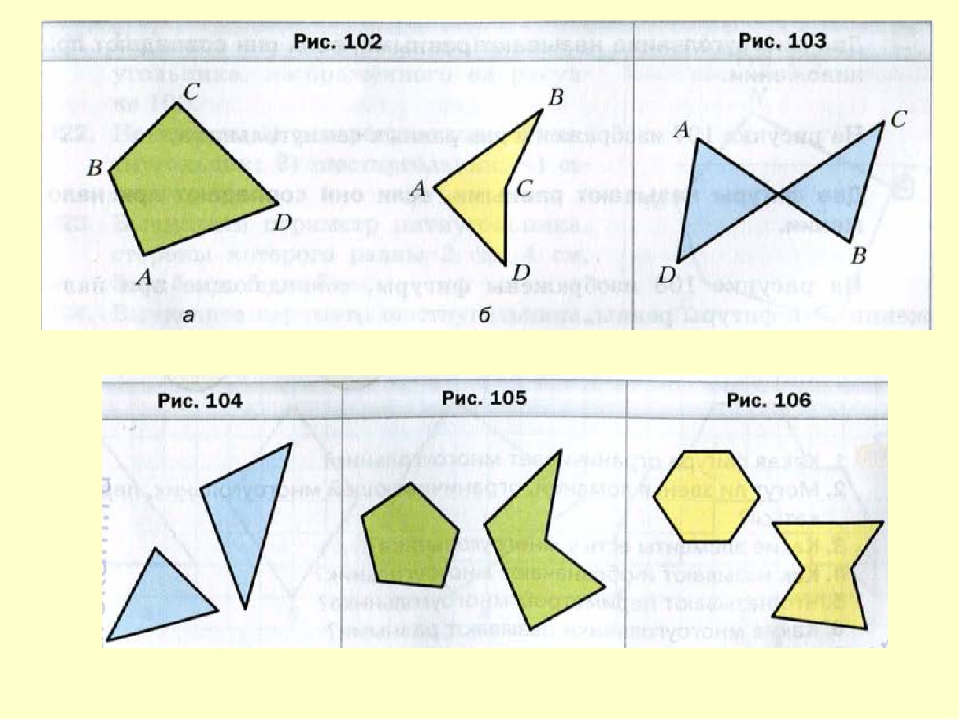 Для вычисления его площади существует множество способов.

Вычисление площади треугольника

Чаще всего приходится работать с прямоугольными треугольниками. Их площадь вычислить несложно — это полупроизведение катетов (сторон, между которыми лежит прямой угол). Таким образом, даже если стороны двух фигур по длине разные, но их произведение равно, они равновеликие. Например, треугольник с катетами 4 и 4 равен по площади многоугольнику с катетами 16 и 1. Так как их полупроизведение, а значит и площадь равна 8.

Если же треугольник произвольный (то есть не является частным случаем — прямоугольным, равнобедренным или равносторонним), можно воспользоваться одной из 5 формул, позволяющих вычислить его площадь.

  1. По двум сторонам и углу между ними.
  2. По стороне и высоте, проведённой к ней.
  3. По трём сторонам и полупериметру.
  4. По полупериметру и радиусу вписанной окружности.
  5. По трём сторонам и радиусу описанной окружности.

То, какую формулу использовать, будет зависеть от данных, предоставленных в задаче. Иногда придётся проводить дополнительное построение, например, провести высоту или использовать свойства, что биссектрисы пересекаются в центре вписанной окружности. Если не даны все 3 стороны, использовать третью формулу не получится.

Важно понять, что фигуры могут быть разными по количеству углов, но всё равно считаться равновеликими — в учёт идёт только площадь, остальные параметры не важны. Например, прямоугольный треугольник с катетами 2 и 4 будет визуально казаться больше, чем квадрат со стороной 2, но их площади совпадают и равны 4 (площадь прямоугольника считается как произведение прилежащих сторон друг на друга). По определению это делает их равновеликими.

Визуальный способ

Существует также наглядный, но неточный способ. Нужно взять листок в клеточку и нарисовать на нём многоугольники. Если рисунок получился большой — не страшно, так будет только проще в дальнейшем. Следующий шаг — посчитать количество клеток, которое заняла каждая фигура и сравнить. Если оно равно, равновеликость доказана. Опять же метод не точный, но для введения в концепцию площадей и их «равности» подойдёт.

Иногда встречается словосочетание «равносоставленная фигура». Такими называют произвольные многоугольники, которые можно составить друг из друга путём разрезания одного из них на одинаковые объекты и перекладывания. Например, если прямоугольник 4 на 1 нарезать на одинаковые части — квадраты 1 на 1, то из полученных маленьких квадратов можно составить один большой со стороной 2. Но это не более чем забавное свойство некоторых фигур и в геометрии фактически почти не используется.


Основные правила математики с примерами. 5 класс — Сайт учителя математики Косыхиной Н.В.

Основные правила математики с примерами. 5 класс

Содержание
  • Натуральные числа
  • Сравнение натуральных чисел
  • Свойства сложения
  • Формула пути
  • Корень уравнения
  • Правила решения уравнений
  • Отрезок, прямая, луч
  • Угол, биссектриса угла
  • Углы: развернутый, прямой, острый, тупой
  • Многоугольники. Равные фигуры
  • Треугольники: остроугольный, прямоугольный, тупоугольный
  • Треугольники: равнобедренный, равносторонний, разносторонний
Натуральные числа

Числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 и т. д., которые используют при счете предметов, называют натуральными.

Сравнение натуральных чисел

Число меньше любого натурального числа.

0<1, 0<100

Из двух натуральных чисел, которые имеют разное количество цифр большим является то, у которого количество цифр больше.

4352⏟4>999⏟3

Из двух натуральных чисел с одинаковым количеством цифр большим является то, у которого больше первая (при чтении слева направо) из неодинаковых цифр

3561>3559

Свойства сложения

Переместительный закон: 

15+10=10+15

Сочетательный закон:

(23+15)+25=23+(15+25)

Формула пути
S=V·t,где S — пройденный путь, V — скорость движения, t — время, за которое пройден путь S

 

Корень уравнения

Корнем (решением) уравнения называют число, которое при подстановке его вместо буквы превращает уравнение в верное числовое равенство.

2·x+10=16

x = 3 — корень, так как 2·3+10=16

Что значит «Решить уравнение»

Решить уравнение — это значит найти все его корни или убедиться, что их вообще нет.

Правила решения уравнений
  • Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.

20слагаемое+xслагаемое=100суммаx = 100 — 20x = 80

  • Чтобы найти неизвестное уменьшаемое, надо к разности при­бавить вычитаемое.

xуменьшаемое—10вычитаемое=40разностьx = 40 + 10x = 50

  • Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.

50уменьшаемое—xвычитаемое=40разностьx = 50 — 40x = 10

  • Чтобы найти неизвестный множитель, надо произведение раз­делить на известный множитель.

xмножитель·7множитель=56произведениеx = 56 : 7x = 8

  • Чтобы найти неизвестное делимое, надо делитель умножить на частное.

xделимое:8делитель=9частноеx = 9 · 8x = 72

  • Чтобы найти неизвестный делитель, надо делимое разделить на частное.

42делимое:xделитель=7частноеx = 42 : 7x = 6

Отрезок, прямая, луч
Отрезок

Отрезок — часть прямой, ограниченная двумя точками(концами) и все точки между этими концами(внутренние точки отрезка)

Свойство длины отрезка

Если на отрезке отметить точку , то длина отрезка равна сумме длин отрезков и .

Равные отрезки

Два отрезка называют равными, если они совмещаются при наложении.

Свойство прямой

Через две точки проходит только одна прямая.

Измерить отрезок

Измерить отрезок означает подсчитать, сколько единичных отрезков в нем помещается

Ломаная

Ломаная — геометрическая фигура, состоящая из отрезков, последовательно соединенных друг с другом

Луч

Луч (полупрямая) — это геометрическая фигура, часть прямой, состоящая из точки(начала луча) и всех точек прямой, лежащих по одну сторону от начала луча.В названии луча присутствуют две буквы, например, . Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.

 

Угол, биссектриса угла
Угол

Фигуру, образованную двумя лучами, имеющими общее начало, называют углом.

Равные углы

Два угла называют равными, если они совмещаются при наложении.

Свойство величины угла

Если между сторонами угла ∠ провести луч , то градусная мера  ∠ равна сумме градусных мер углов ∠ и ∠, то есть ∠ = ∠+ ∠.

Биссектриса угла

Луч, который делит угол на два равных угла, называется биссектрисой угла.

Углы: развернутый, прямой, острый, тупой
Развернутый угол

Угол, стороны которого образуют прямую, называют развернутым. Градусная мера развернутого угла равна 180°.

Прямой угол

Угол, градусная мера которого равна 90°, называют прямым.

Острый угол

Угол, градусная мера которого меньше 90°, называют острым.

Тупой угол

Угол, градусная мера которого больше 90°, но меньше 180°, называют тупым.

 

Многоугольники. Равные фигуры
Равные многоугольники

Два многоугольники называют равными, если они совмещаются при наложении.

Равные фигуры

Две фигуры называют равными, если они совмещаются при наложении.

Треугольники: остроугольный, прямоугольный, тупоугольный
Остроугольный треугольник

Если все углы треугольника острые, то его называют остроугольным треугольником.

Прямоугольный треугольник

Если один из углов треугольника прямой, то его называют прямоугольным треугольником.

Тупоугольный треугольник

Если один из углов треугольника тупой, то его называют тупоугольным треугольником.

Треугольники: равнобедренный, равносторонний, разносторонний
Равнобедренный треугольник

Если две стороны треугольника равны, то его называют равнобедренным треугольником.

Равносторонний треугольник

Если три стороны треугольника равны, то его называют равносторонним треугольником.

Периметр равностороннего треугольника

Если сторона равностороннего треугольника равна , то его периметр вычисляют по формуле

Разносторонний треугольник

Если три стороны треугольника имеют разную длину, то его называют разносторонним треугольником.

Прямоугольник. Квадрат. Периметр
Прямоугольник

Если в четырехугольнике все углы прямые, то его называют прямоугольником.

Свойство прямоугольника

Противоположные стороны прямоугольника равны.

Периметр прямоугольника

Если соседние стороны прямоугольника равны и , то его периметр вычисляют по формуле

Квадрат

Прямоугольник, у которого все стороны равны, называют квадратом.

Периметр квадрата

Если сторона квадрата равна , то его периметр вычисляют по формуле .



Умножение. Свойства умножения
Умножение

 


  • Если один из двух множителей равен 1, то произведение равно второму множителю.
  • Если один из множителей равен нулю, то произведение равно нулю.
  • Если произведение равно нулю, то хотя бы один из множителей равен нулю.
Свойства умножения
  • Переместительный закон умножения:
  • Сочетательный закон умножения: 
  • Распределительное свойство умножения относительно сложения:  

2·(3+10) = 2·3 + 2·103·11 + 3·4 = 3·(11 + 4)

  • Распределительное свойство умножения относительно вычитания:

2·(15—7) = 2·15 — 2·73·10 — 3·4 = 3·(10 — 4)

Деление. Деление с остатком
Деление

Для натуральных чисел равенство   является правильным, если является правильным равенство

15 : 5 = 3 -правильное равенство, так как  равенство 5 · 3 = 15 верное

В равенстве    число называют делимым, число — делителем, число и   запись  — частным от деления, отношением, долей.

На ноль делить нельзя.

Для любого натурального числа  правильными являются равенства:

,

Деление с остатком

, где  — делимое, — делитель, — неполное частное, — остаток, .

154делимое=50делитель · 3неполное частное + 4остаток,    4<50

Если остаток равен нулю, то говорят, что число делится нацело на число .

Площадь. Площадь квадрата, прямоугольника
Свойства площади фигуры

Равные фигуры имеют равные площади;

Площадь фигуры равна сумме площадей фигур, из которых она состоит.

Площадь прямоугольника

Площадь прямоугольника равна произведению длин его соседних сторон, выраженных в одних и тех же единицах.

Площадь квадрата

,

где  — площадь квадрата,  — длина его стороны.

Объем. Объем прямоугольного параллелепипеда, куба
Свойства объема фигуры

Равные фигуры имеют равные объемы;
Объем фигуры равен сумме объемов фигур, из которых она состоит.

Объем прямоугольного параллелепипеда
  • ,

где — объем параллелепипеда, , и  — его измерения, выраженные в одних и тех же единицах;

, где — площадь поверхности прямоугольного параллелепипеда.

  • ,

где  — площадь основания параллелепипеда, — его высота.

Объем куба

,

где  — объем куба,  — длина его ребра.

Дроби: правильная, неправильная, сравнение дробей
Правильная дробь

Дробь, числитель которой меньше знаменателя, называют правильной

Неправильная дробь

Дробь, числитель которой больше знаменателя или равен ему, называют неправильной.

Сравнение дробей
  • Из двух дробей с одинаковыми знаменателями больше та, числитель которой больше, и меньше та, числитель которой меньше.
  • Из двух дробей с одинаковыми числителями больше та, знаменатель которого меньше, и меньшая та, знаменатель которой больше.
  • Все правильные дроби меньше единицы, а неправильные — больше или равны единице.
  • Любая неправильная дробь больше любой правильной дроби.
Сложение и вычитание дробей с одинаковыми знаменателями
  • Чтобы найти сумму двух дробей с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тот же.
  • Чтобы найти разность двух дробей с одинаковыми знаменателями, надо из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить тот же.
Сложение и вычитание смешанных чисел
  • Чтобы найти сумму двух смешанных чисел, надо отдельно сложить их целые и дробные части.
  • Чтобы найти разность двух смешанных чисел, надо от целой и дробной части уменьшаемого вычесть соответственно целую и дробную части вычитаемого.
Преобразование неправильной дроби в смешанное число

Чтобы неправильную дробь, числитель которой не делится нацело на знаменатель, преобразовать в смешанное число, нужно

  • числитель разделить на знаменатель;
  • полученное неполное частное записать как целую часть смешанного числа, а остаток — как числитель его дробной части.

227= смешанное число? 7322—211  227=317      

 

Преобразование смешанного числа в неправильную дробь

Чтобы преобразовать смешанное число в неправильную дробь нужно

  • целую часть числа умножить на знаменатель дробной части;
  • к полученному произведению прибавить числитель дробной части;
  • эту сумму записать как числитель неправильной дроби;
  • в его знаменателе записать знаменатель дробной части смешанного числа.

523= неправильная дробь?523=5*3+23=15+23=173

Десятичные дроби: свойства, сравнение, округление
Свойства десятичной дроби

Если к десятичной дроби справа приписать любое количество нулей, то получим дробь, равную данной.

Значение дроби, которая заканчивается нулями, не изменится, если последние нули в его записи отбросить.

2,23  = 2,230 = 2,230000005,50000=5,50000=5,5

Сравнение десятичных дробей

Из двух десятичных дробей больше та, у которой целая часть больше.

Чтобы сравнить две десятичные дроби с равными целыми частями и разным количеством цифр после запятой, надо

  • с помощью приписывания нулей справа уравнять количество цифр в дробных частях,
  • после чего сравнить полученные дроби поразрядно.

Сравнить 5,03 и 5,0375.5,03⏟2=5,0300⏟4    и     5,0375⏟4  ; 5,0300 < 5,0375.

Округление десятичных дробей

Для того чтобы десятичную дробь округлить до единиц, десятых, сотых и т. д., надо

  • все следующие за этим разрядом цифры отбросить.
  • если при этом первая из цифр, которые отбрасывают равна 0,1, 2, 3, 4, то последнюю из цифр, которые оставляют, не меняют;
  • если же первая из цифр, которые отбрасывют, равна 5, 6, 7, 8, 9, то последнюю из цифр, которые оставляют, увеличивают на единицу.

Округлить 5,248 и 3,952:а) до десятых:5,248≈5,2; 3,952≈4,0;б) до сотых:5,248≈5,25;3,952≈3,95.

Десятичные дроби: сложение, вычитание
Сложение десятичных дробей

Чтобы найти сумму двух десятичных дробей, нужно:

  •  уравнять количество цифр после запятых;
  •  записать слагаемые друг под другом так, чтобы каждый разряд второго слагаемого оказался под соответствующим разрядом первого слагаемого;
  •  сложить полученные числа так, как складывают натуральные числа;
  • поставить в полученной сумме запятую под запятыми.

Сложить 2,5 и 3,623.2,500⏟3 и 3,263⏟3;2,500+3,2635,763

Вычитание десятичных дробей

Чтобы найти разность двух десятичных дробей, нужно:

  •  уравнять количество цифр после запятых;
  • записать вычитаемое под уменьшаемым так, чтобы каждый разряд вычитаемого оказался под соответствующим разрядом уменьшаемого;
  •  выполнить вычитание так, как вычитают натуральные числа;
  • поставить в полученной разности запятую под запятыми.

Вычесть 3,27 и 3,009.3,270⏟3  и 3,009⏟3;3,270—3,0090,261

Десятичные дроби: умножение, деление
Умножение десятичных дробей

Чтобы перемножить две десятичные дроби, надо:

  • перемножить их как натуральные числа, не обращая внимания на запятые;
  • в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятых в обоих множителях вместе.

Умножить 1,5 и 2,25.2×2,2511,5+1125225·33,375 —количество цифр после запятой

Чтобы умножить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую вправо на 1, 2, 3 и т. д. цифры.

Умножить 1,235 на 10, 100, 1000.а) на 10:1,235 ×10⏟1=12,35б) на 100:1,235 ×100⏟2 = 123,5в) на 1000:1,235 ×1000⏟3=1235,0 = 1235

Чтобы умножить десятичную дробь на 0,1; 0,01; 0,001 и т. д., надо в этой дроби перенести запятую влево соответственно на 1, 2, 3 и т. д. цифры.

Умножить 512,3 на 0,1,   0,01 и  0,001.а) на 0,1:512,3 ×0,1⏟1=51,23б) на 0,01:512,3 ×0,01⏟2=5,123в) на 0,001:512,3 ×0,001⏟3=0,5123

Деление десятичных дробей

Чтобы разделить десятичную дробь на десятичную, надо:

  • перенести в делимом и в делителе запятую вправо на столько цифр, сколько их содержится после запятой в делителе;
  • выполнить деление на натуральное число.

Разделить 24,2 на 0,02.24,2 : 0,02⏟ 2= 2420,0 : 2 = 2420 : 2 = 1210.

Чтобы разделить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую влево на 1, 2, 3 и т. д. цифры.

 Разделить 25,5 на 10, 100, 1000.а)  на 10:25,5 : 10⏟1=2,55;б) на 100:25,5 : 100⏟2=0,255;в)  на 1000:25,5 : 1000⏟3=0,0255;

 

Среднее арифметическое

Средним арифметическим нескольких чисел называют результат деления сумму этих чисел на количество слагаемых.

Найти среднее арифметическое  чисел 15, 25 и 20.

15+25+20⏞сумма чисел3⏟количество чисел = 603= 20
Примечание:

Задача. Автомобиль 200 км ехал со скоростью 50 км/ч. Затем 120 км он ехал со скоростью 30 км/ч. Найти  среднюю скорость.

Здесь

 Vсредняя =Sобщtобщ .

1) 200 + 120 = 320(км) -весь путь;

2) 200 : 50 = 4(ч) — время, затраченное на 1-ую часть пути;

3) 120 : 30 = 4(ч) — время, затраченное на 2-ую часть пути;

4) 4 + 4 = 8(ч) — все время;

5) 320 : 8 = 40(км/ч) — средняя скорость.

Ответ: 40 км/ч.

Процент

Процентом  называют сотую часть величины или числа 1%=

Найти 4% от числа 20.20 : 100 = 0,2  (0,2 —это 1% от числа 20);0,2 × 4 =0,8( 0,8—искомое число).Или   4% = 4100 = 0,04;0,04 ×20 = 0,8.

A + Click Grade 5 Questions

  • Home
Какая из этих задач деления имеет ответ 8? Что даст наибольшее число? Что нужно добавить к 378, чтобы получить 400? Какова сумма из 436 и 523? Что вы получите, если увеличите 316 на 500? Какое число отсутствует? 587+? = 630 Какое число, умноженное на 9, равно 72? Что даст наибольшее число? Что даст наибольший ответ? Какое наибольшее число? Округлите числа 345 и 765 до ближайших 100, а затем сложите их.Вычислить: 4,5 x (3,5 — 2,5) + 1,5 Какое значение наименьшее? Какая фракция закрашена? Какое из этих выражений дает наименьшее значение? Какое число составляет половину одной четверти одной восьмой от 128? Какое число, разделенное на 5, совпадает с этим числом минус 5? Сократите дробь до наименьшего числа. Девушка может сыграть 66 отмечает каждую минуту. Сколько нот она может сыграть за 6. . . Какое наименьшее десятизначное число, у которого две цифры совпадают? Какое наименьшее целое число, в 2 раза превышающее сумму его цифр? Джон покупает две игрушки.Какая у него максимальная сдача с 10 долларов? Какое десятичное число ближе всего к 10? Какая часть клавиш пианино черная? Дерево было посажено в 1798 году. Сколько ему будет лет в 2020 году? Анна купила 28 мармеладов. Какое утверждение НЕПРАВИЛЬНО? Оцените количество флажков на картинке. Какое наибольшее число на картинке? Найдите самый легкий набор. Сколько чисел от 222 до 444 заканчиваются на 0? Сью хочет заработать ровно 33 очка. Утки дают разные баллы. Который . . .Страницы книги нумеруются последовательно от 1 до 99.Сколько . . . Это стандартный набор домино. Сколько домино имеет ровно 6 точек? Какое наименьшее число на картинке? Четверо детей хотят поделить пять плиток шоколада, чтобы все получили одинаковое. . Какая буква чаще всего используется в этом вопросе? Какая буква находится точно посередине между буквами D и P в английском языке. . Найдите произведение десяти наименьших чисел в таблице. 111111 + 11111 — 1111 + 111 — 11 + 1 = Какая из этих задач деления имеет ответ 9? Что даст наибольшее число? Что вы получите, если увеличите 333 на 499? Что даст наибольшее число? Какой ответ дает наименьший ответ? Какое наибольшее число? Вычислите: 6.5 x (5,5 — 4,5) + 2,5 Какое значение наибольшее? Какая часть правильной формы не закрашена? Какое из этих выражений дает наибольшее значение? Какое число составляет половину одной четверти одной восьмой от 320? Найдите наименьшее значение. Какова сумма 250, 350, 450 и 550? Что вы можете добавить к 17,17, чтобы получить 20 ? Какой остаток вы получите, если разделите 112 на 7. Какое из этих выражений дает наименьшее значение? Что из следующего равно половине миллиона? Какой ответ дает наименьший? Какая часть клавиш пианино белая? Страницы книги нумеруются последовательно от 1 до 100.Сколько . . . Шесть детей хотят разделить пять плиток шоколада, чтобы все получили одинаковое. . .Какова разница в денежном выражении между пятью десятидолларовыми купюрами и четырьмя. . . Дыню разрезают на девять частей, и одна треть кусочков съедается. Как . . У нас с другом одинаковое количество кубиков. Сколько кубиков мне нужно. . .Сколько цифр в английском языке написаны одинаково. . . Какие два целых числа с суммой 25 дают наибольшее произведение? Мальчику 13 лет, а его матери 31 год, что соответствует его возрасту с.. .Найдите третье число у основания пирамиды, если каждое число является суммой. . .Какое число отсутствует в числовой строке? Если бы вы записывали числа по буквам, как далеко вам пришлось бы зайти раньше. . Перед отъездом в поездку одометр водителя показывает 78987. В конце . . .Бензобак в машине вмещает 17 галлонов. Автомобиль в среднем составляет 25 миль до. . .Сколько есть чисел, которые без остатка делятся на 7? (5 x 5 + 5 x 5 + 5 — 5 x 5) / 5 + 5 =? Какое среднее значение этих чисел? Найдите произведение чисел.Каково произведение всех этих чисел? Найдите произведение чисел. Что такое одна восьмая от сорока? Какова сумма наибольших однозначных, двузначных и трехзначных целых чисел? Сколько дюжин яблоки есть, если в бумажном пакете 28 яблок? Добавьте минус один к двум и вычтите минус три. Каков результат? Что вы получите, если перемножить все числа? В Лондоне в 2012 году США выиграли 46 золотых, 28 серебряных и 29 бронзовых медалей. Отлично . . .Что будет после миллиона? 1991 — это число, которое остается таким же при чтении назад и вперед.. . .Сколько существует счетных чисел от 11 до 66, включая первое и. . В первой стопке 5 монет, во второй 8, в третьей 11 и 16. . .Какой набор состоит из наибольшего количества кубиков? Цифры ниже образуют узор. -1, 111,. . . Какие из следующих . . .Какая упорядоченная пара находится внутри треугольника? Высота кубического аквариума Анны — 48 см. Анна в два с половиной раза больше. . .Какая точка на числовой прямой ближе всего к (0 + 1 — 2 x 3)? Начало системы координат — это точка, в которой x и y равны нулю.. . .Какое число имеет наименьшее значение? Я перемножил все цифры числа 754531. 7 x 5 x 4 x 5 x 3 x 1 Найдите. . . Восемь яблок стоят трех апельсинов. Сколько яблок можно обменять на 15. . . В номере 5 разрядов десятков. Есть 5 в разряде сотен. . . .Цифры ниже образуют образец. -2, 11,. . . Какие из следующих . . .Цифры ниже образуют образец. -11, 10, 31,. . . Какой из . . .Какая упорядоченная пара находится внутри треугольника? Высота кубического аквариума Анны — 40 см.Анне три с половиной раза. . .144 делить на 4 — это то же самое, что и 4, умноженные на X. Найдите X. Какое число находится точно на полпути между 66 и 166? Найдите два числа, сумма которых равна 7, а произведение равно 10. Выберите число от 1 до 4. Сложите 9. Повторяйте прибавление 9 до получения результата. . .Какое ближайшее к 300 число делится на 17? В беге на 5000 м участвуют 8 финалистов. Сколько метров они проезжают. . . На 2 страницах книги 60 строк и 48 знаков в каждой строке. Как .. Я прочитал 123 из 1234-страничной книги. Сколько еще страниц я должен прочитать, пока я. . . Пятьсот двадцать семь человек садятся в поезд в Женеве, двести двести. . Анна прошла в школу 123 шага. Треть пути в школу была. . .Плавательный бассейн длиной 25 метров. Сколько метров проплывет победитель, если. . Джон экономил 7 долларов каждую неделю и тратил 10 долларов на посещение кинотеатра вместе со своим. . За гостевым столом французского короля Людовика XIV могут сесть шесть человек. Сколько . . . Анна откладывает указанное количество швейцарских центов каждый день.Сколько центов она. . Какая часть большого квадрата красная? В женской школе с 80 учениками 4 отсутствуют. Какая доля. . .Сколько из следующих чисел дает в сумме двадцать девять? 5 7 11 13 17 19 21 Разделите 222 доллара между 19 студентами и оставьте себе как можно меньше сдачи. Как . . Джейн готовит для 22 пиратов. Ей нужно 2 яйца на пирата и минимум 3. . .В каждом бумажном пакете одинаковое количество яблок. Всего 35 яблок. . Лорен купила 3 ​​рожка мороженого за 4 доллара.77. Какова цена каждой шишки, если. . .Один полный круг велодрома — 400м. Дженни проехала семь с половиной кругов. Какая . . Жили-были три поросенка. Свинья хотела построить дом. . .Сколько недель в 1000 дней? Что больше? Найдите результат. В школе 1234 ученика. Если 12 отсутствуют, а 123 погасло. . Джерри делит 6 орехов между 4 мальчиками. Сколько орехов получает каждый мальчик? Дэн вел машину со скоростью 50 миль в час в течение трех с половиной часов.Сколько . . Семья из семи человек съела 84 блинов, а в доме осталось 35 блинов. . Семья едет в 130 милях от родного города до дома дедушки. 20 . . Учитель разбил класс из 32 детей на команды. Что она умеет? У всех на фото, включая животных, по 32 зуба. Сколько зубов вообще. . Найдите A. Россия имеет площадь 17 075 200 квадратных километров. Канада имеет площадь. . .Какова площадь цветной фигуры? У какой фигуры самая большая площадь? Сколько у нее прямых углов? У какой фигуры наименьший периметр? Какие два отрезка линии параллельны? Опишите окрашенную область прямоугольника в виде дроби.Помните, . . .Сколько треугольников можно нарисовать, используя любые три из пяти точек в качестве. . .Сколько кирпичей нужно, чтобы построить эти стены? У Томаса 24 метра забора, и он хочет сделать прямоугольный двор из. . . Буква «А» симметрична. Симметричную фигуру можно сложить пополам и. . Какая часть фигуры является зеленой? Найдите периметр фигуры. Какая фигура представляет собой прямоугольник, состоящий ровно из 1 квадрата, 2 треугольников и 1 трапеции? Какое положение стрелки? Помните, что их может быть больше одного.. . Какая из этих трехмерных фигур имеет больше всего краев? Каково расстояние между двумя стрелками? Помните, что их может быть больше. . Какой отрезок имеет длину 8? Найдите координату середины отрезка AB Какая форма имеет хотя бы 1 прямой угол? Какое изображение симметрично? Какая из этих частей имеет наибольшую площадь? Какая фигура имеет большую площадь? Найдите 2 фигуры с одинаковым периметром. На картинке показан план квадратного сада. Расстояние между яблонями 5. . .Какая форма НЕ имеет прямых углов? Фигуры с хотя бы одним прямым углом: Какая фигура может образовывать куб, если его сложить по пунктирным линиям без.. .Какова площадь заштрихованной фигуры? Какие стороны фигуры кажутся перпендикулярными? Какую группу фигур НЕЛЬЗЯ сделать, разрезав прямоугольник? Примерно на сколько градусов должна повыситься температура, чтобы достичь 44 градусов? Найдите длину белой линии посередине коридора. Собираю прямоугольники из цветных квадратов. Все квадраты по краям есть. . .Сколько треугольников? Выберите фигуру с наибольшей площадью. На картинке фигуры ABCDEF и UVWXYZ имеют одинаковую форму и размер.Который . . Какая фигура внизу имеет тот же периметр, что и фигура справа? Дети запустили 40 воздушных шаров. Они нашли 20 воздушных шаров. Схема показывает. . Пятиугольник (от греческого слова pente — число 5) — это любой пятиугольник. . .Какая фигура имеет все стороны одинаковой длины? Сколько в ней разных плиток? Сколько в ней линий симметрии? Сколько в ней квадратов? Какой прямоугольник имеет наибольшую площадь? Какая буква в слове MATH имеет более одной линии симметрия? Оцените, сколько красных кругов можно разместить вокруг синего круга так, чтобы.. .Какая фигура делится на 4 одинаковые формы? Две цифры совпадают, если. . .Какое наибольшее трехзначное число имеет как вертикальное, так и горизонтальное положение. . .Сколько здесь квадратов? Сколько вершин у фигуры? Сколько карточек на картинке? На картинке эскиз парка. Какой из представленных ниже фигур нет. . .Какая фигура, показанная справа, имеет наибольшую площадь? Сколько прямых углов в этой фигуре? На каком изображении преобразования показан ТОЛЬКО перевод (слайд)? Сколько затененных квадратов на рисунке? Для какой буквы я сделал использовать как можно больше зеленой краски? Удаление квадрата приводит к уменьшению периметра синего.. . Удаление квадрата не изменяет периметр синей формы? Я вырезал четыре одинаковых треугольника из углов прямоугольника, чтобы получился a. . .Сколько коробок измерения 1 х 2 х 3 можно упаковать в тару размером 3. . .Найдите фигуру с наибольшим количеством вершин. Какова максимальная длина стороны куба, которая может поместиться в это поле? . . .Я вырезал квадрат из угла цветного квадрата. Какая часть начального. . .Сколько синих кругов на этой картинке? Какая форма имеет наибольшее количество прямых углов? Какая форма имеет наименьший периметр? Муравей идет из точки А в точку Б по указанному пути.Сколько раз . . Сетка можно сложить в куб. Какая буква стоит напротив отмеченного лица. . .Какая часть досок еще не окрашена? Какая форма имеет наименьшее количество вершин? Сколько тупых углов в этой форме? [Тупой угол — один. . . Какое наибольшее количество фигур с одинаковым периметром? Какая форма имеет наименьшую площадь? Какие два отрезка линии перпендикулярны? У Томаса 32 метра забора, и он хочет сделать прямоугольный двор из.. .Какая часть фигуры синяя? Найдите область симметричной формы. Найдите точку, которая находится точно посередине между двумя красными стрелками. Как . . Какая точка находится ближе всего к координате середины отрезка AB? Найдите две похожие формы с разными площадями. Аналогичные формы имеют. . На картинке изображен план квадратного сада. Расстояние между яблонями. . .Что имеет наибольшую площадь? Какие стороны фигуры кажутся параллельными? Симметричную фигуру можно сложить пополам и обе стороны точно совпадут.. . Показанная башня сделана из кубиков, уложенных друг на друга. Несколько из . . . Оцените периметр цветной фигуры. На рисунке фигуры ABCDEF и UVWXYZ имеют одинаковую форму и размер. Который . . Какие две формы имеют самую короткую общую границу? Уличные кварталы на Стейт-стрит имеют одинаковую длину. Какое расстояние. . .Сколько существует фигур с площадью больше 10 квадратных единиц? Как далеко от отметки «4» линейки находится стрелка? (Файл.. Найдите лишний. На картинке изображен сплошной куб 5x5x5. Сколько маленьких кубиков нужно использовать в. . .Какая форма имеет наибольшую площадь? Сколько линий появляется на картинке? Примерно какой длины эта струна? Сколько маленьких кубиков было использовано для построения этой твердой фигуры? Какая часть квадрата самая большая? Как вы называете треугольником с двумя равными сторонами? Каков периметр следующей фигуры с прямыми углами? Каково полное перемещение мальчика, который проходит 1 квартал на север, 2 квартала на восток,.. .Сколько кубиков? Сверху положено по четыре квадрата из цветной бумаги одинакового размера. . . Какое наибольшее количество мячей касается мяч? У Джерри есть куб со стороной в двенадцать дюймов. Если он разрежет куб на меньшие. . .Какая из фигур имеет наименьший периметр? Сколько линий симметрии у снежинок? Сколько шаров находится во втором слое пирамиды, начиная с нижнего? Отсортируйте фигуры по их объединенным площадям от наименьшего к наибольшему. цветные многоугольники есть на картинке? quot; Элементарно.. Какова сумма количества ребер куба и количества граней куба. . .Концертная зона была оборудована 19 рядами стульев. В каждом ряду было по 9 стульев. В . . Высота этой лестницы составляет 3 ступени. Сколько кирпичей потребуется для изготовления. . На графике показана общая сумма денег, которую Джон скопил за пять недель. Если . . .Кевин покупает 3 мешка мрамора. Каждый шарик весит в среднем 50 граммов. Как . . На рождественской неделе есть среда. Это заявление есть. . . Палочка сливочного масла весит 1 килограмм (1000 грамм).Джейн разрезает его пополам. . . В каждое ведро Алекс кладет не менее 1 яблока. Максимальное количество яблок в. . Джим бросил восемь центов. Один на один выпало в три раза больше монет, чем это число. . .Три коробки шоколадных конфет эквивалентны шестисотам конфет. Файл. . Анна, не глядя, достает из коробки один мяч. Из какого ящика находится файл. . Насколько быстрее движется минутная стрелка по сравнению с часовой стрелкой? В 2010 году население итальянской столицы Рим составляло 2 761 477 человек.. Что вы получите, если сложите от 3 до 33 три раза? Кевин покупает три мешка шариков. Каждый шарик весит в среднем 50 граммов. . . .Концертная зона была оборудована 19 рядами стульев. В каждом ряду было 18 стульев. В . . .Разрезаем 1800 грамм сливочного масла пополам. Затем мы разрезаем одну из половинок. . .Вначале ведра пустые. Алекс кладет минимум 2 яблока в каждое ведро. Файл. . . Три коробки шоколадных конфет эквивалентны 150 конфетам. Номер . . На картинке изображена карта метро.На какой линии меньше станций? Сколько разных способов можно набрать 5, бросив два кубика? (Не считайте 4… Каков был остаток на банковском счете Боба 18 мая? Автобус будет ехать один час, затем поезд — три с половиной часа … На нем 40 светлых и темно-серых квадратов. тарелка. Сколько еще квадратов … Жили-были три поросенка. Свинья построила дом из соломы … Двое туристов плыли вниз по течению 1/8 своего пути. После этого они …. .В этой игре есть светлые и темные шары. Сколько всего шаров? Оцените соотношение площадей двух частей. Если четыре ряда шахматной доски заняты шахматными фигурами, какую часть. . На круговой диаграмме показано количество мужчин, женщин и детей в округе. Какая часть . . . Одно из значений в этом треугольнике неверно. Какой должна быть правильная стоимость? У Ребекки есть 81 монета, которую она может разделить между 9 детьми. Сколько монет будет у каждого. . .В поездке на лодку приходится 11 детей и 1 взрослый.Если всего 96. . .В классе девочек на две больше, чем мальчиков. Всего студентов двадцать. Сколько . . . Шестнадцать команд участвуют в хоккейном турнире. Если ничьих быть не может, сколько. . .Есть три отдельных больших красных коробки, а внутри каждой большой коробки есть. . Джим Смит пьет волшебное зелье, уменьшающее его вес вдвое. Он был . . Джон работает с девяти утра до половины седьмого вечера. . . Джим косил участок своего газона, показанный на диаграмме, в течение 12 минут.Сколько . . Американский президент Франклин Д. Рузвельт умер в 1945 году в возрасте 63 лет. . . Каждый столб забора имеет ширину 12 сантиметров. Расстояние между стойками — 8. . Какое правило используется для машины In-Out?

% PDF-1.3 % 1 0 obj >] / Pages 3 0 R / Type / Catalog / ViewerPreferences >>> endobj 2 0 obj > поток 2010-10-29T12: 56: 38-04: 002013-03-04T16: 28: 10-05: 002013-03-04T16: 28: 10-05: 00Adobe InDesign CS4 (6.0.4)

  • JPEG256256 / 9j / 4AAQSkZJRgABAgEASABIAAD / 7QAsUGhvdG9zaG9wIDMuMAA4QklNA + 0AAAAAABAASAAAAAEA AQBIAAAAAQAB / + 4AE0Fkb2JlAGQAAAAAAQUAApGg / 9sAhAAMCAgICAgMCAgMEAsLCxAUDg0NDhQY EhMTExIYFBIUFBQUEhQUGx4eHhsUJCcnJyckMjU1NTI7Ozs7Ozs7Ozs7AQ0LCxAOECIYGCIyKCEo MjsyMjIyOzs7Ozs7Ozs7Ozs7Ozs7OztAQEBAQDtAQEBAQEBAQEBAQEBAQEBAQEBAQED / wAARCAEA AMYDAREAAhEBAxEB / 8QBQgAAAQUBAQEBAQEAAAAAAAAAAwABAgQFBgcICQoLAQABBQEBAQEBAQAA AAAAAAABAAIDBAUGBwgJCgsQAAEEAQMCBAIFBwYIBQMMMwEAAhEDBCESMQVBUWETInGBMgYUkaGx QiMkFVLBYjM0coLRQwclklPw4fFjczUWorKDJkSTVGRFwqN0NhfSVeJl8rOEw9N14 / NGJ5SkhbSV xNTk9KW1xdXl9VZmdoaWprbG1ub2N0dXZ3eHl6e3x9fn9xEAAgIBAgQEAwQFBgcHBgI7AQACEQMh MRIEQVFhcSITBTKBkRShsUIjwVLR8DMkYuFygpJDUxVjczTxJQYWorKDByY1wtJEk1SjF2RFVTZ0 ZeLys4TD03Xj80aUpIW0lcTU5PSltcXV5fVWZnaGlqa2xtbm9ic3R1dnd4eXp7fh2 + f3 / 9oADAMB AAIRAxEAPwDrfqx9WPq3kfVvpN9 / ScG223Bxn2WPxqnOc51TC5znFkkkpKdL / mn9Vf8Aym6f / wCw tP8A6TSUr / mn9Vf / ACm6f / 7C0 / 8ApNJSv + af1V / 8pun / APsLT / 6TSUr / AJp / VX / ym6f / AOwtP / pN JSv + af1V / wDKbp // ALC0 / wDpNJSv + af1V / 8AKbp // sLT / wCk0lK / 5p / VX / ym6f8A + wtP / pNJSv8A mn9Vf / Kbp / 8A7C0 / + k0lK / 5p / VX / AMpun / 8AsLT / AOk0lK / 5p / VX / wApun / + wtP / AKTSUr / mn9Vf / Kbp / wD7C0 / + k0lK / wCaf1V / 8pun / wDsLT / 6TSUr / mn9Vf8Aym6f / wCwtP8A6TSUr / mn9Vf / ACm6 f / 7C0 / 8ApNJSv + af1V / 8pun / APsLT / 6TSUr / AJp / VX / ym6f / AOwtP / pNJSv + af1V / wDKbp // ALC0 / wDpNJSv + af1V / 8AKbp // sLT / wCk0lK / 5p / VX / ym6f8A + wtP / pNJSv8Amn9Vf / Kbp / 8A7C0 / + k0l K / 5p / VX / AMpun / 8AsLT / AOk0lK / 5p / VX / wApun / + wtP / AKTSUr / mn9Vf / Kbp / wD7C0 / + k0lOb1b6 sfVuvP6KyvpOCxt2c9ljW41QD2jDzX7XAM1G5gPxCSnS + qf / AIlejf8Apvxf / PNaSnWSUpJSklKS UpJSklKSUpJSklKSUpJSklKSUpJSklKSUpJSklKSUpJSklKSUpJTk9Z / 5R6F / wCnCz / 2xz0lK + qf / iV6N / 6b8X / zzWkp1klKSUpJSklKSUpJSklKSUpJSklKSUpJSklKSUpJSklKSUpJSklKSUpJSklK SU5PWf8AlHoX / pws / wDbHPSUr6p / + JXo3 / pvxf8AzzWkp1klKSUpJSklKSUpJSklKSUpJSklKSUp JSklKSUpJSklKSUpJSklKSUpJSklKSU5PWf + Uehf + nCz / wBsc9JSvqn / AOJXo3 / pvxf / ADzWkp1k lKSUpJSklKSUpJSklKSUpJSklKSUpJSklKSUpJSklKSUpJSklKSUpJSklKSU5PWf + Uehf + nCz / 2x z0lK + qf / AIlejf8Apvxf / PNaSnWSUpJSklKSUpJSklKSUpJSklKSUpJSklKSUpJSklKSUpJSklKS UpJSklKSUpJTk9Z / 5R6F / wCnCz / 2xz0lK + qf / iV6N / 6b8X / zzWkp1klOa3ruPZlHHox8m6ttvoOy a691LbAdpaTO7Q6EhsDxTePVk9kgWSGDPrHgvuY0V3jHst9CvMLP0DrJLNodM / SETET3S4wk4JV4 9kF / 1w6Pj4ublWl4 / Z + QcW2qG + o6wEtGwboIMGNexQOWIBXDlZkgdxaa / wCs3S8bI6hjXudXZ0ut ltwIHua9rXD0 / dr9IDtqUjkAJ8Fo5eZESP0lz9YsV1eO7GoyMqzJoZlCmlgc9lVglrrJeGj4T8Eu MK9g2bIFaKq + svSrsnExWPcHZ7Hupc5u0bqztdW6dQ + Z0hh4BYUcEwCezZx + q4mR093VCTVj1 + rv dZALRS99bydpd3YURIEWtljIlw9WvV9YMV1VmRk0ZOJTXX6wtyKtrXMkD27S7X3fRMHyQ4wuOE3Q ILA / WXErbacrHycV1dFmSxl9Ya61lTd7 / T95EgdiQUOMJ9gnYg9GH / OnDZTdbk42Tjmij7WK7Ws3 WVAhpczbY5vLhyQl7gV93kSKI7N / Az7M3f6mHkYeyI + 0Bg3TP0fTss4hOBvosnAR6gttFYpJSklK SUpJSklKSUpJSklKSUpJTk9Z / wCUehf + nCz / ANsc9JSvqn / 4lejf + m / F / wDPNaSnWSU4 + F0 / q / Tb PsmK / GdgG99wdYH + s1ljza + sNHtOrjDt3yTACGac4TFm7azOg9SGNV0Z9tJ6ZRayxtg3eu5ldnrM rLY2jUAbp47IcBqui45o3xfpIMr6nNycXOe4VHPvflHHsJOwNyLC9m / 2TuaHEeUlA4rBXR5qiO2n 4NrI + rFOZn5udltY91ljbcQyZaW0Mpiz28b2h3ngE447JKwcwYxAh2 + 1jidG6t0sY93T349lv2PH xMqu4vDC7HaWtsre1pP5x0LUBEx2TLLCd3e5I + qNn1SL7Qcu1tgsov8AVsZLHtyb768gWVDXaGlu mqXtpPM6aeh3VTaweg2t + rTuhdQtD7LW3tsur4m2yywOAIb + 9wiIemitnmHu8YCrundb6lhW4PUr cathY0V2Y4e5xtY5r2WOD9oAln0dfikYyIooE8cJXG0Gd0brPV63 / tF + NW + rHyKsdtBeWutvqdTv sc9stADuACgYyluuhlhjOl7hBb9VMtuNm49NwuOXhtx67Mm2x76nt + kxpcHfo3c / FD2zRXDmBYNb Ho6fQsDLwG3MyaqqmvLS308i / JJImZ + 0tEduE + AIYs04yqvyA / J1U5iUkpSSlJKUkpSSlJKUkpSS lJKUkpyes / 8AKPQv / ThZ / wC2OekpX1T / APEr0b / 034v / AJ5rSU6ySnlcC61 / VHYedlX3HNdkMpvx coOpIbudt9NsOpcxoiR37qIHXVtTA4LA2rcfytrfabOmdIzrhl5VmTdmX9OxzZbbfsaLXND2slx3 MY0mQJ0Quolfw8cwKFUCs / Ltz / q3632vKZl9OyK8N72WW0Osa + 6pjbLGSwkvqeD7gldxUIiOXYUR f4JuqNux + ttwK3Z2RTVhVvDa840O3OtvBe91t1e4kCEpaSpGOjjvTfs6f1h + 0txsSvEv2D1PfV9o + z23tDD7WXGfcDBPj4p87piw1Zsfg514bn4vRszHy8 + tuVktxbQch7HFrW5G7d6Tg0u3V / SHKadQ GSPpMgQNBe3kj / b76frIzbdccCqxvTDW5tjmExByHWEFm4XQzmUOP1fgn2bxba7 / ANjXv6r1bFqz WW22voyupuqxbmudupdXlNDqS6foOrBj5hAyI + 1cMcJEabR1 + xM / Itoxs7qdeff9uq6hfVRjOuc9 lgF5YykUOJEFumg0RugTfVbQJEa0r9iSz6xWN + s4sFtn2Fto6c6rY / 0pPN + / b6ci6GczCXH60DB + q8d / 5fRBi5ea7rDa67M1ttnVMiv1LbZxHUVWP31NY6x3u2D2jaPJIE8X1XSjHg6fKPNL0 / Kuqrwc uvOuuysrPtotxrLTa11IuuY6K3E7NjGh0iOEonbXqicQSRWgDZ + r2XczqQxs3Isybsiqyxl1eQ2 / GtDXNl7a + aiNwAHCMDqtzRHDYFfTVsdc + tlfRM0Yb8Z1xLBZuDw3kkRG0 + Clarnf + OJR / wBwX / 8A bg / 8gkp6TpHUW9W6fV1BrDULt3sJmNrnM50 / dSU3ElKSUpJSklKSUpJTk9Z / 5R6F / wCnCz / 2xz0l K + qf / iV6N / 6b8X / zzWkp1klIK8LDqvflVUVMvs0fa1jQ939ZwElCguM5EVa7cPEY9tjaK2vY99jX BjQQ + yd7gY5dOp7pUEcUu6n4eJYbDZRW82lhsLmNO81mWF0jXaRp4JUFCRHVHldK6ZnWC3Nw6Mmw Dah4VMe4NBJiXNOmqRiDuF0ck4jQpLsPEyKRjZFFdtIgCp7GuYI49pBCRAK0SkDYK5xsYtqYamba CHVDaIYQC0FmmhgxolQVxFb7HifZziehX6BkmnY3Zqd59sR9LVKgriN3ajh5hrdUaKzW9 / quZsbt Ly7fvIj6W7WfFKgriN7o6 + l9MqyDl1YlDMhxLnXNrYHlzuSXhsyZS4RaTkmRV6JPseJ9nOJ6FfoG Sadjdmp3n2xH0tUqCOI3dq + x4cbfQrgWeuBsbHqk7vU4 + lJ55SoK4pd2FHTun4trr8XFpptfO + yu trHOnUy5oBKQiAkzlIUSypwsPHtfdj0VVWW / zj2Ma1zv6xABKQACjORFEo8npXTc2z1svGqusjbu e0OMDtqitRf83 + if9waP + 2x / ckpuY + PRi1Noxq21VMnaxggCTJgfEpKSJKUkpSSlJKUkpSSnJ6z / AMo9C / 8AThZ / 7Y56SlfVP / xK9G / 9N + L / AOea0lOskpF9mxv9Ez / NH9ySlfZsb / RM / wA0f3JKV9mx v9Ez / NH9ySlfZsb / AETP80f3JKV9mxv9Ez / NH9ySlfZsb / RM / wA0f3JKV9mxv9Ez / NH9ySlfZsb / AETP80f3JKV9mxv9Ez / NH9ySlfZsb / RM / wA0f3JKV9mx

    • 5 класс AGL по математике

      Приборная доска

      5 класс AGL Математика

      Перейти к содержанию Приборная доска

      • Авторизоваться

      • Приборная панель

      • Календарь

      • Входящие

      • История

      • Помогите

      Закрыть