Категории: 5 класс.

Как решить задачу 5 класса: Задачи по математике 5 класс

 Комментировать

Урок по теме «Среднее арифметическое» 5 класс

Автор: edu1

Методическая копилка — Математика

Тема урока: «Среднее арифметическое»

Учебник:

Авт. Виленкин Н.Я. и др.

5 класс

учитель математики

МКОУ «Замостянская сош»

Селитренникова Галина Алексеевна

Цели урока

Образовательные:

  • ввести понятие среднего арифметического; вывести правило для его нахождения;
  • научить решать задачи, связанные с нахождением среднего арифметического;
  • отрабатывать навыки действий с десятичными дробями;
  • развивать умение составлять задачи, используя цифровые данные из жизни.

Развивающие:

  • содействовать развитию у школьников логического мышления, математической речи;
  • способствовать развитию познавательного интереса;
  • развивать умение анализировать, делать выводы на основе полученных результатов;
  • способствовать формированию правильной математической речи;
  • создать условия для развития у учащихся умений осуществлять самоконтроль и самооценку учебной деятельности.

Воспитательные:

  • содействовать осознанию учащимися ценности изучаемого предмета;
  • активизировать познавательную и творческую деятельность учащихся;
  • показать значение математических знаний в жизни, побудить применять эти знания в жизни.

Тип урока: урок открытия новых знаний.

Формы работы: индивидуальная, фронтальная, групповая.

Оборудование: презентация к уроку, проектор, экран.

Предварительная подготовка.

Для эффективности работы было дано предварительное домашнее задание:

  1. класс поделен на 3 группы по рядам;
  2. измерить и записать рост каждого обучающегося в группе.

Ход урока: 

 I. Мотивирование к учебной деятельности (организационный момент) — 1-2 минуты

 Посмотрите, всё ль в порядке:

Книжки, ручки и тетрадки.

Прозвенел сейчас звонок.

Начинается урок.

 Учитель приветствует обучающихся, проверяет готовность к уроку, отмечает отсутствующих.

Каждый ученик получает лист «Моё настроение», на котором отмечает смайлик, соответствующий его настроению.

II.Актуализация и фиксирование индивидуального затруднения в пробном учебном действии — 4-5 минут

1.Устное решение задач.

Задача 1.

У Иванова Ивана по математике в журнале стоят оценки

4   5   3   4   5   4   3  3   4

Как вы думаете, какую оценку в четверти получит Иван? И почему?

Задача 2.
К доске приглашаются три ученика.
Вопросы:
Кто самый высокий?
Кто самый низкий?
Кто средний по росту?

Какие «особенные слова» вы заметили в условиях всех задач?

     Часто мы и в жизни слышим фразы со словом “средний”, например: средний возраст, средний рост, средняя температура и т.д. Как вы понимаете эти выражения?

     В математике тоже есть свои понятия со словом “средний” и сегодня мы познакомимся с одним из этих  понятий.  

2. Устный счёт.
Тема сегодняшнего урока состоит из двух слов. Вы её сможете прочитать, если верно решите примеры и вставите буквы в таблицу ответов.

7,3 · 3          Е
64,24 : 8      А
12 – 2,6       И
68,2 : 2        О
45,4 + 0,6    С

12 · 0,1        Р
43,1 · 10      Д
81,1 : 0,1     Н
60 – 0,9       Ф
4,13 + 3,87  М
6,45 – 6,4    Т
0,1 · 0,1       К
7 · 0,01        Ч

46

1,2

21,9

431

811

21,9

21,9

 

 

 

 

 

 

 

 

8,03

1,2

9,4

59,1

8

21,9

0,05

9,4

0,07

21,9

46

0,01

34,1

21,9

 

 

 

 

 

 

 

 

 

 

 

 

 

 

III. Постановка учебной задачи — 4-5 минут 

   Ребята, назовите тему урока. («Среднее арифметическое»)

   Запишем число и тему урока.
   Рассмотрим задачу:

У Ани 14 конфет, у Кати 9 конфет, а у Оли 10 конфет. Сколько конфет достанется каждой девочке, если конфеты разделить между ними поровну? 

Решение обсуждается с учащимися.
14 + 9 + 10 = 33 (конфеты)

33 : 3 = 11 (конфет)
Число 11 называют средним арифметическим чисел 14; 9 и 10.

Рассмотрим еще задачу :

Миша, Петя и Коля были в походе. Подойдя к лесу, они решили сделать привал. У Миши было 2 пирожка, у Пети 4 и у Коли 6. Все пирожки мальчики разделили поровну и съели. Сколько пирожков съел каждый?
Совместно с учащимися получается:
2 + 4 + 6 = 12 (пирожков)
12 : 3 = 4 (пирожка)
Число 4 называется средним арифметическим чисел 2; 4 и 6.

Ребята, что же называется средним арифметическим чисел? ( Ответы учащихся)

Средним арифметическим нескольких чисел называют частное от деления суммы этих чисел на число слагаемых.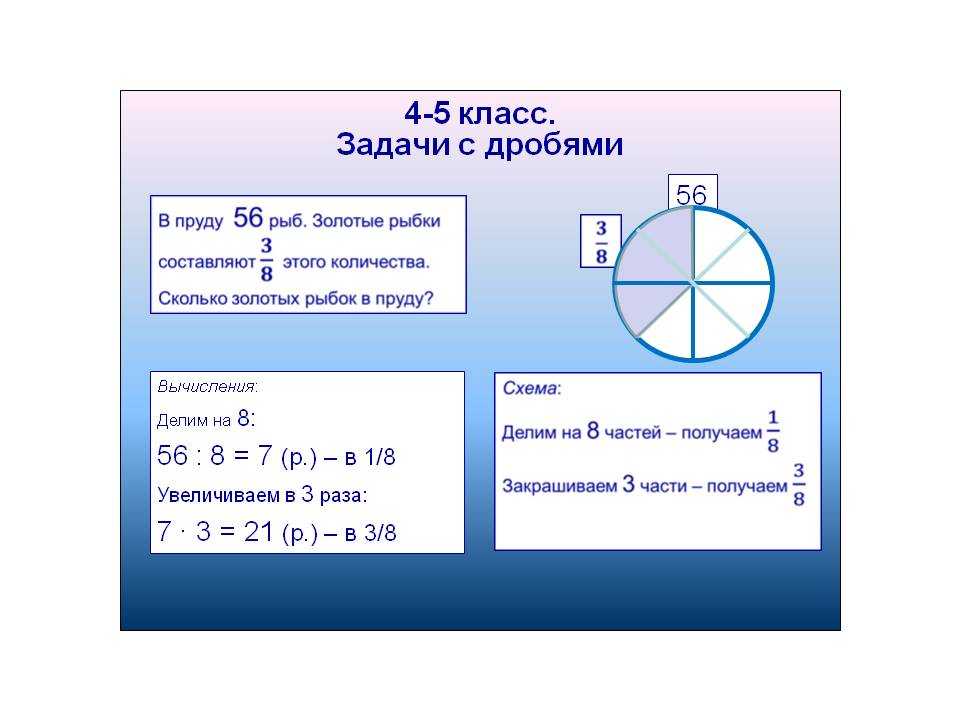
Как найти среднее арифметическое нескольких чисел? (Ответы ребят)
Среднее арифметическое = (Сумма чисел) : (количество слагаемых)


(Учащиеся записывают в тетрадях)

IV. Открытие нового знания (построение  проекта выхода из затруднения)  7-8 минут

Из какой сказки вы прослушали отрывок?

 1.      Братья сеяли три поля по 200 га каждое. На первом поле собрали 7220ц пшеницы, на втором – 7560ц, а на третьем – 7090ц пшеницы. Определите урожайность на каждом поле и найдите среднюю урожайность.
Вопросы:
Как найти урожайность одного поля?
Как найти среднюю урожайность трёх полей?
7220 : 200 = 36,1(ц.) – урожайность на первом поле.
7560 : 200 = 37,8(ц.) – урожайность на втором поле.
7090 : 200 = 35,45(ц.) – урожайность на первом поле.
(36,1 + 37,8 + 35,45) : 3 = 36,45(ц.) – средняя урожайность трёх полей.

  1. Задание на сообразительность:

Подключите свои знания, смекалку, сообразительность, чувство юмора и попытайтесь отыскать «среднее арифметическое» не чисел, а предметов, которые нас окружают.

Итак, среднее арифметическое:

  • Велосипеда и мотоцикла. (Мопед.)
  • Трамвая и поезда. (Электричка.)
  • Апельсина и лимона. (Грейпфрут.)
  • Туфельки и сапога. (Ботинок.)
  • Пианино и баяна. (Аккордеон.)
  • Холодильника и вентилятора. (Кондиционер.)
  • Портфеля и рюкзака. (Ранец.)
  • Носка и чулка. (Гольф.)

 V. Первичное закрепление — 4-5 минут

1. Задача № 1502 (из учебника)

Участница соревнований по фигурному катанию на коньках получила оценки

5,3; 4,8; 5,4; 5,0; 5,3; 5,4; 5,3; 5,2; 5,1.
Найдите среднюю оценку этой участницы.
Как найти среднее арифметическое нескольких чисел?
Решение с коментированием:
(5,3 + 4,8 + 5,4 + 5,0 + 5,3 + 5,4 + 5,3 + 5,2 + 5,1) : 9 = 5,2

 2.Задача № 1504 (из учебника)

Поезд шёл 4 ч со скоростью 70 км/ч и 3ч со скоростью 84 км/ч. Найдите среднюю скорость поезда на пройденном за это время пути.

Как найти среднюю скорость?
Решение у доски по действиям или выражением:
(70 · 4 + 84 · 3) : 7 = 76(км/ч)

Средняя скорость =(Весь пройденный путь): (всё время движения).

 3. Игра – задание «Полёт в космос»

         А сейчас мы с вами отправимся в космос, посетим планету Меркурий. Но до полета надо размяться, привести себя в форму, космическую.

Физминутка

Быстро встали, улыбнулись
Выше-выше потянулись.
Ну-ка, плечи распрямите,
Поднимите, опустите.
Вправо, влево повернитесь,
Рук коленями коснитесь.
Сели, встали. Сели, встали.
И на месте побежали.

             Известно, что на планете Меркурий средняя температура +15°. Можно предположить, что возможна жизнь человека на этой планете. Но на самом деле температура на Меркурии колеблется от 150º мороза до 350°жары.

 VI. Самостоятельная работа с самопроверкой по образцу (эталону) — 4-5 минут.

Тест по теме: «Среднее арифметическое чисел»

Ответ на вопрос обведите кружком

 1. Найдите среднее арифметическое чисел 1,5 и 2,3

а) 1,9         б) 3,8     в) 3

2. Среднее арифметическое чисел 2, 4, 6, и 0 равно:

а) 3     б) 6     в) 4

3. Незнайка по математике получил следующие оценки 5, 3, 1, 4, 4, 1. Найдите среднюю оценку Незнайки.

а) 3   б) 4   в) 5

4. Вини — Пух съел 18 конфет, Пятачок — 9 конфет, Кролик — 3 конфеты. Сколько конфет в среднем съел каждый?

а) 12     б) 5     в) 10

5. Найдите среднее арифметическое чисел: 20,22 и 18,26

а) 23,78     б) 19,24     в) 12,43

1

2

3

4

5

а

а

а

в

б

VII.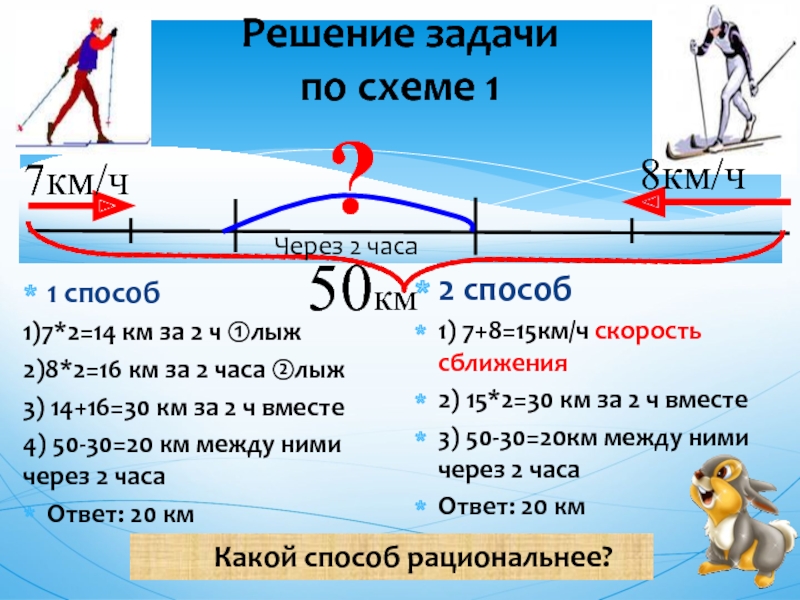    Включение нового знания в систему знаний и повторение – 7-8 минут.

1.Задача.

1)Точка С – середина отрезка АВ. Найдите координату точки С.
2)Найдите среднее арифметическое чисел 12,36 и 22,57.

Сравните полученный результат

2. Практическая работа в группах.

 Предварительная подготовка.

Для эффективности работы было дано предварительное домашнее задание:

  1. класс поделен на 3 группы по рядам;
  2. измерить и записать рост каждого обучающегося в группе.

Вопрос:
Что мы можем определить, используя данные предварительного задания?
Ответ:
Мы можем определить средний рост в группе.
Что для этого нужно сделать?
Выполняйте задание.

 VIII. Рефлексия учебной деятельности на уроке (итог) — 2-3 минуты.

               Что нового вы узнали на уроке?

  • Сегодня я узнал…
  • Мне было интересно…
  • Я узнал и могу научить товарища…
  • Я понял, что…
  • Теперь я могу…
  • Меня удивило…

Каково ваше настроение в конце урока?

Домашнее задание.

   Учитель комментирует домашнее задание:
1. № 1524 (а/б), №1526

2. Вычислить средний возраст вашей семьи.

3. Узнать, где в жизни необходимо умение находить среднее   арифметическое  (подготовить сообщение по желанию).

     Итог урока. Выставление оценок. Спасибо Вам, дети, за урок. Я буду рада, если полученные на уроках математики знания помогут Вам в жизни при решении проблем. Вы – молодцы. Особо хочу отметить … Полные и правильные ответы давали …

 

Решение задач алгебраическим способом. 5 класс

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Решение задач алгебраическим способом

Урок в 5 классе
Учитель математики
первой категории
Шитоева А.О.
«Гимназия № 6»
Г. Пермь
Цель: обобщение знаний о способах
решения задач
Задачи:
повторить этапы работы с задачей
учиться выбирать модель и переменную
выбирать рациональный способ решения
тренироваться в решении задач
алгебраическим способом

3. Математические модели

А
Схема
В
x
С
186
скорость
Таблица
Чертеж
По
течению
Х+3
Против
течения
Х-3
х
время
5
6
2х
2х-7
Уравнение
От чего зависит
выбор модели?
◦
•а)
32
Х + 2х+2х-7=43
от условия задачи
•б) от желания учителя
• в) от главного вопроса задачи
•г) от знаний ученика
D
путь
5·( х +3)
6 · (х-3)
Р= 43 см

4. Задача. Мама старше Юли в 3 раза, а Юля старше Светы на 5 лет. Вместе им 55 лет.

Сколько лет маме и девочкам ?(х-5) + х + 3х =55
х + (х+5) +3х = 55
Пусть х лет маме
Пусть х лет Юле
Пусть х лет Свете
х + (х +5) +3(х + 5) =55
Как выбрать
неизвестную
величину?
а) самая маленькая величина задачи
б) самая большая величина задачи
в)величина, с которой сравниваются все
остальные
г) спросить у соседа
д)величина из главного вопроса задачи

5. А: установи соответствие

Ι. Соедините стрелкой реальную ситуацию с ее
математической моделью:
На листе опроса 3 ситуации и 5 алгебраических
моделей (уравнений). Каждой ситуации
подберите свою модель.
Одну задачу можно
решить с помощью:
а) разных способов,
б)справочников и интернета
в) разных моделей

6. ΙΙ. Составьте различные уравнения для задачи:

Мама, папа и Алиса
собирали на берегу
ракушки. Папа собрал
на 7 ракушек
больше…
Внимательно читай
текст задачи
Если Х ракушек
собрала мама
______________________
…
…
Если составил три
уравнения, тымолодец.

7. В: реши задачу алгебраически

1.
2.
3.
4.
5.
6.
Найди главный
вопрос задачи
Выбери подходящую
модель
Выбери переменную
Составь уравнение
по модели
Реши уравнение
Запиши ответ
План решения задачи
Совет: начни уравнение
с большего количества
ног..

8. С: Составь задачу

На движение по
алгебраической
модели
(пешеход, пароход,
веломобиль…)
Различные
задачи могут
быть решены:
На совместную работу
по алгебраической
модели
( мастер, ученик,
швея, машинистка…)
а) только с помощью различных моделей
б) иногда с помощью одинаковых
моделей
в) с помощью подсказки
г) затрудняюсь ответить

9. Основные рекомендации по решению задач алгебраически:

Выбор модели зависит от условия задачи и
ее главного вопроса
За неизвестное лучше выбирать самую
маленькую величину или величину главного
вопроса
Полезно руководствоваться планом решения
задачи
Часто к одной задаче можно составить
разные модели
Разные задачи иногда можно решить с
помощью одной модели

10.

Домашнее задание: Помните:
Чем
труднее задача,
тем больше
удовольствие ее
решить.
Домашнее задание:
Напишите отзыв на этот урок

English     Русский Правила

Математические словесные задачи для 5 класса

Словесные задачи по математике относятся к информации, представленной посредством обычного рассказывания историй, и учащиеся должны понять и преобразовать ее в математические уравнения. Уровень сложности упражнений снижен, а математические идеи максимально упрощены. Чтобы понять, как используются концепции, каждая тема предлагает значительное количество примеров. Мы сосредоточимся на четырех основных операциях, дробях, десятичных дробях и т. д. в пятом классе.

Словесные задачи на сложение и вычитание для 5-го класса

Словесные задачи на сложение и вычитание для 5-го класса необходимы учащимся для развития базовых арифметических навыков на сложение и вычитание.

Преимущество текстовых задач на сложение и вычитание заключается в том, что учащиеся понимают, как понимать данную информацию в текстовых задачах и записывать ее в математической записи для дальнейшего решения.

Q1. У Джерри было 87 шариков. Сегодня он собрал еще 74. Сколько шариков у него сейчас?

Ответ: Из вопроса следует, что у Джерри было 87 шариков.

Поскольку он собрал еще 74 шарика,

Таким образом, общее количество шариков равно 87 + 74

= 161

Всего у Джерри 161 шарик.

Q2. У мистера Себастьяна было 257 долларов. Он купил духовку за 158 долларов. Сколько денег у него осталось?

Ответ: Согласно вопросу,

у мистера Себастьяна было 257 долларов. Из 257 долларов он купил духовку за 158 долларов.

Таким образом, оставшиеся деньги станут:

= $257$ — $158$

= $99$

Словесные задачки на умножение и деление для 5-го класса

Словесные задачки на умножение и деление для 5-го класса улучшат понимание учащимися умножения и деления при решении задач из реальной жизни. Умножение и деление — одни из четырех основных арифметических операций, которые находят применение в нашей повседневной жизни.

Q1. В бейсбольной команде 9 игроков. В турнире участвуют 6 команд. Сколько игроков всего?

Ответ: В данном вопросе дано, что бейсбольная команда состоит из 9 игроков. Если в турнире участвуют 6 команд,

Таким образом, общее количество игроков станет $9 \ умножить на 6$

= 54 игрока,

Следовательно, всего 54 игрока.

Q2. Фермер должен посеять 500 семян в 20 рядов. Сколько семян нужно посеять в каждом ряду?

Ответ: Согласно заданному вопросу, фермер должен посеять 500 семян в 20 рядов.

Чтобы найти количество семян в каждом ряду, нужно разделить количество посеянных семян на ряды.

Следовательно, $\dfrac{500}{20}$ = 25

Следовательно, в каждом ряду нужно посеять по 25 семян.

Задания на дроби для 5-го класса

Задачи на дроби для 5-го класса помогают учащимся раскрыть понятия дробей и их использование в реальных жизненных ситуациях.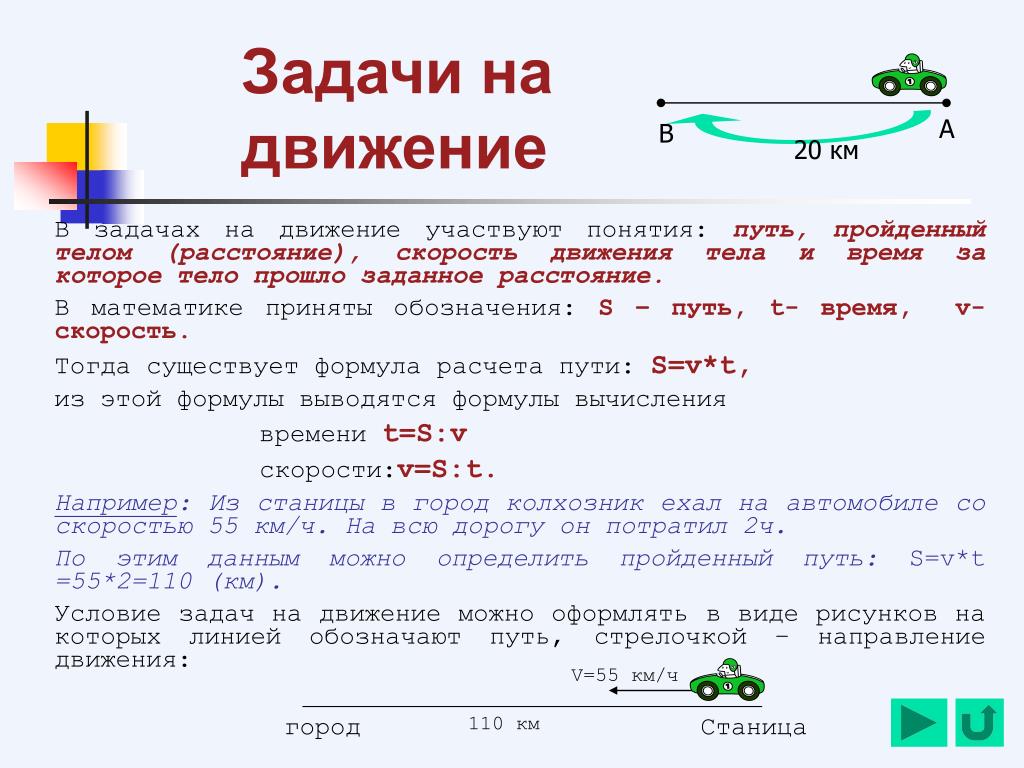 Дроби означают часть целого, и они находят свое место повсюду, что делает эту тему важной для изучения.

Q1. Шон покупает 25 наклеек в понедельник и 17 во вторник. В среду он отдает Джеймсу $\dfrac{5}{6}$-й из своих наклеек. Сколько у него осталось?

Ответ: Всего наклеек, купленных Шоном = количество наклеек, купленных в (понедельник + вторник)

= 25 + 17

= 42 наклейки.

С тех пор, как он отдал Джеймсу $\dfrac{5}{6}$-й из своих наклеек.

т.е. $\dfrac{5}{6}$ й из 42 наклеек для Джеймса.

= $\dfrac{5}{6} \times 42$

= $5 \times 7$

= 35

Итак, он дал Джеймсу 35 наклеек.

У Шона осталось 42 — 35 наклеек

= 7

Следовательно, у него осталось 7 наклеек.

Словесные задачи для 5 класса с решением

Q1. Мистер Томас продал 832 штуки печенья в январе и 917 штук в феврале. Сколько печенья он продал за эти два месяца?

Ответ: Согласно вопросу,

Мистер Томас продал 832 печенья в январе и 917 печенья в феврале.

Таким образом, общее количество проданных печенья составит: 832 + 917

= 1749

Q2. В пазле 40 деталей. Сколько частей в 3 таких пазлах?

Ответ: Судя по вопросу, в пазле 40 частей.

Таким образом, чтобы найти количество деталей в 3 пазлах, мы должны умножить его на 40.

Следовательно, $40 \×3$

= 120

Следовательно, 120 элементов в 3 пазлах.

Q3. Средняя частота сердечных сокращений в минуту равна 72. За сколько минут сердце бьется 1440 раз?

Ответ: Дано,

Средняя частота сердечных сокращений в минуту равна 72.

Таким образом, для 1440 раз $\dfrac{1440}{72}$

= 20 минут.

Значит, за 20 минут сердце бьется 1440 раз.

Q4. У Ханны в пакете 72 конфеты. $\dfrac{1}{3}$rd из них она оставляет себе, а остальным делится с друзьями. Сколько конфет она даст своим друзьям?

Ответ: Судя по вопросу, у Ханны в сумке 72 конфеты.

$\dfrac{1}{3}$rd из них она оставляет себе.

т. е. $\dfrac{1}{3}$rd из 72

= $\dfrac{1}{3} \times 72$

= $1 \times 24$

= 24

Итак, она оставила себе 24.

Следовательно, конфет у Ханны = 72 — 24

= 48

Значит, она подарит своим друзьям 48 конфет.

Практические словесные задачи для класса 5

Q1. Население города составляет 78 384 человека. Если из них 38 400 женщин, найдите мужское население.

Ответ: 39 984

Q2. Среди каждых 5 велосипедов, произведенных компанией, один велосипед является специальной серией. Если компания производит 150 велосипедов, сколько велосипедов специальных выпусков?

Ответ: 30 велосипедов

Резюме

Чтобы дети усвоили любую тему, необходимо решить различные задачи в рамках этой темы.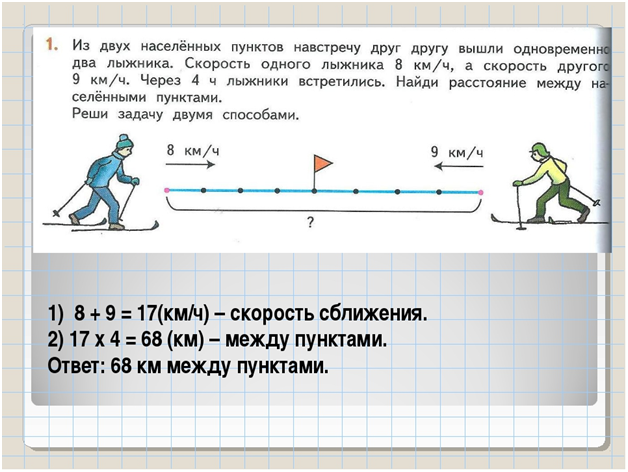 В этой статье были рассмотрены задачи на сложение, вычитание, умножение, деление и дробь. Эти задачи дадут понимание и большую ясность в повседневной жизни при решении арифметических задач. В конце статьи мы добавили решенные примеры и практические вопросы для лучшего понимания.

Класс 5 Время — основы, задачи и решенные примеры

  • Время — это период, который измеряется в минутах, днях, годах и т. д.
    60 секунд = 1 минута
    60 минут = 1 час
    24 часа = 1 день
    365 дней = 1 год
  • Время также можно определить как функцию, которая принимает три числа: день (от 1 до 31), месяц (от 1 до 12) и год (скажем, 2004) и возвращает целое число.
    Например,
    Рассмотрим 23.01.2018, эта функция имеет 3 числа: день (23), месяц (01) и год (2018). Когда время определяется таким образом, оно также называется датой.
  • Когда мы переводим высшие единицы времени в младшие, мы умножаем. Когда мы переводим младшие единицы времени в высшие, мы делим.

ПРИМЕР 1: Запишите 4 часа 5 минут 60 секунд в секундах.

РЕШЕНИЕ:

Преобразовывая часы и минуты в секунды, мы получаем:

4 часа = 4X60 минут = 4X60X60 секунд = 14400 секунд получить:
= (14400+300+60) секунд
=14760 секунд

Следовательно, 4 часа 5 минут 60 секунд в пересчете на секунду составляют 14760 секунд.

ПРИМЕР 2: Дата рождения Нехи — тридцатый день восьмого месяца тысяча девятьсот девяносто шестого года. Запишите в формате даты.

Решение:

. имеет 365 дней. Но в некоторых годах 366 дней. Эти годы называются високосными. Дополнительный день приходится на февраль. Високосные годы происходят с интервалом в 4 года.
Как узнать, является ли год високосным? Если конкретный год можно разделить на 4, оставив нулевой остаток, то год является високосным. Например, 1996÷4=499
с остатком 0. Значит, 1996 год високосный.

  • Всего 12 месяцев. Это январь (1), февраль (2), март (3), апрель (4), май (5), июнь (6), июль (7), август (8), сентябрь (9), октябрь ( 10), ноябрь(11), декабрь(12).
  • В январе, марте, мае, июле, августе, октябре и декабре 31 день. Апрель, июнь, сентябрь и ноябрь имеют 30 дней. В феврале 28 дней, а в високосный год их 29.дней.
    Например,
    В 1996 году
    В феврале 29 дней
    , потому что 1996 год високосный.

    • Общая информация: простой способ запомнить, в каких месяцах 31 день, а в каких 30 дней. : 1 23 30 дней


    В сентябре 30 дней.
    Количество дней, оставшихся до конца сентября = (30-23) дней = 7 дней
    Рассматриваем первые 10 дней октября.
    Следовательно, общее количество дней между 23 сентября и 10 октября = (7+10) дней
    = 17 дней [ANS]

    ПРИМЕР 2: Прибавьте 4 года 5 месяцев прибавьте 7 лет 8 месяцев.
    Из 7 лет 2 месяцев вычесть 4 года 5 месяцев

    РЕШЕНИЕ: Сложение:

    • Сложите цифры в позиции месяцев.
    • Здесь 8+5= 13 месяцев.
    • Но всего 12 месяцев.
    • Итак, будем считать 13 месяцев = (12 месяцев + 1 месяц) = (1 год + 1 месяц)
    • Запишите 1 месяц в позиции месяцев и добавьте оставшийся 1 год к (7+4) годам в позиции лет.

    4 года

    5 месяцев

    7 лет

    8 месяцев

    +

    = 11 лет

    13 месяцев (недействительно)

    +1 год(дополнительные 12 месяцев от позиции месяцев)

    -12 месяцев (переведено на лет)

    12 лет

    1 месяц

    Ответ: 12 лет 1 месяц

    Вычитание:

    • Вычитание цифры в позиции месяца
    • Здесь 2-5=-3. Но, -3 месяца не имеет смысла
    • Итак, мы возьмем 12 месяцев (1 год) заимствования из года позиции.
    • Теперь -3+12(заимствованные месяцы) = 9 месяцев.
    • В позиции лет 7-4=3 года. Но мы взяли 1 год (12 месяцев) брать из летнего положения. Итак, мы должны вычесть 1 год из позиции лет. Таким образом, 3-1= 2 года

    7 лет

    2 месяца

    4 года

    5 месяцев

    —

    = 3 года

    -3 месяца (недействительно)

    -1 год(компенсация за одолженные 12 месяцев)

    +12 месяцев(взял)

    2 года

    9 месяцев

    Ответ: 2 года 9месяца


    Примечание.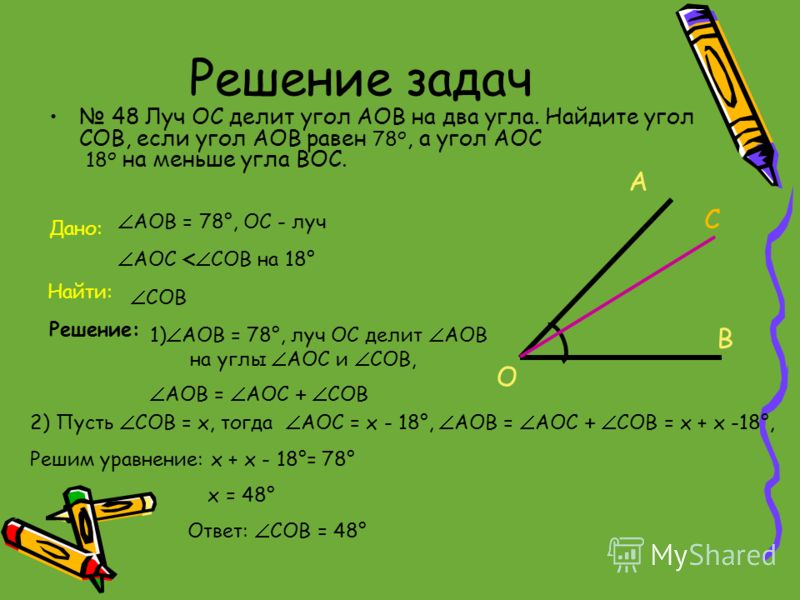 В дополнение к датам 12 месяцев создают перенос 1 года, который добавляется к позиции
    года. При вычитании 1 год заимствования из позиции лет добавляется как 12 месяцев в позиции месяцев

    • Время может быть представлено в двух форматах: 24-часовом формате и 12-часовом формате.
      24-часовой формат: 00 час, 01 час, 02 час, 03 час, 04 час, 05 час, 06 час, 07 час, 08 час, 09 час, 10 час, 11 час ……………., 22 час , 23 часа
      12-часовой формат: 12:00, 1:00, 2:00, 3:00, 4:00, 5:00, 6:00, 7:00, 8:00, 9утра, 10:00, 11:00, 12:00, 13:00, 14:00………….9 вечера, 22:00, 23:00.
    • В 12-часовом формате am означает «anti meridiem», что в переводе с латыни означает «до полудня».
      pm означает «post meridiem», что в переводе с латыни означает «после полудня».
    • Сравнение 12-часового и 24-часового форматов времени.

    • ПРИМЕР 2: Напишите 13:23 в 24-часовом формате. Напишите 4:56 часов в 12-часовом формате.

    РЕШЕНИЕ:

    Если мы добавим 12 часов, т. е. 12:00 к 12-часовому формату времени (только pm.am будет таким же), то результат будет в 24-часовом формате. Следовательно, 1:23+12= 13:23 в 24-часовом формате.

    4:56 часов в 12-часовом формате = 4:56 утра

    Примечание:

    • Время в формате утра в 12-часовом формате будет равно 24-часовому формату.
    • Чтобы преобразовать pm в 24-часовой формат, добавьте 12:00 ко времени, указанному в pm.
    • Чтобы преобразовать время больше 12 в 24-часовой формат, вычтите из него 12, чтобы получить такое же время в 12-часовом формате

    Q1) Ариан начал свою домашнюю работу в 13:23. Он закончил в 14:34. Сколько времени он делал домашнее задание?

    Q2) Бани требуется 3 часа 45 минут, чтобы добраться до аэропорта от своего дома. Если она хочет добраться до аэропорта к 10:00, во сколько она должна выйти из дома?

    Q3) Поезд едет из города A в город B. Поезд отправляется в 17:06. Поезду требуется 78 часов 19 минут, чтобы добраться до города B.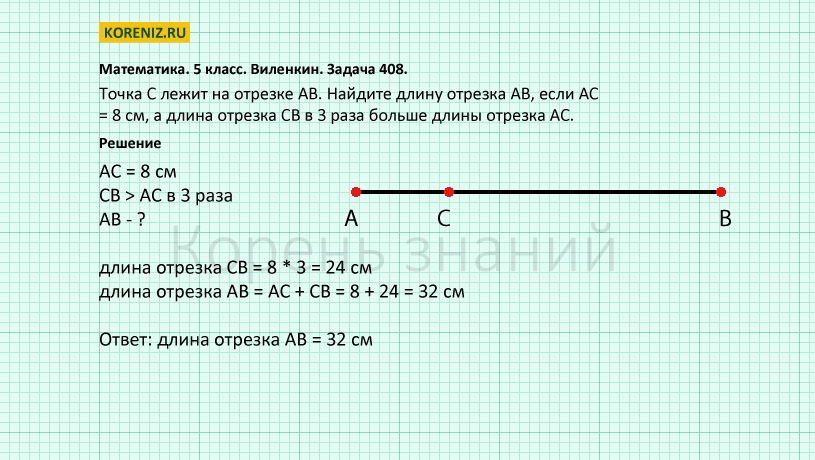 Когда поезд прибудет в город B?

    Q4) Чинмею требуется 2 часа 30 минут, чтобы добраться до города B из города A. Сегодня он добрался до города B через 45 минут. Сколько времени ему потребовалось сегодня, чтобы добраться до города B?

    Q5) Запишите прошедшее время для следующего времени начала и окончания.

    Q6) Запишите 6 часов 7 минут 8 секунд в виде минут и секунд.

    Q7) Запишите дату следующего високосного дня в формате дд/мм/гггг.

    Q8) Сколько дней находится между 9 th февраля 2016 г. и 10 th марта 2016 г.

    Q9) Прибавьте/вычтите 2 года 3 месяца и/из 4 лет 10 месяцев.

    Q10) Напишите 17:01 и 6:07 в 24-часовом формате. Напишите 13:08 часов и 8 часов 9минут в 12-часовом формате.

    • Когда мы переводим более высокие единицы времени в его более низкие единицы, мы умножаем.
    • Когда мы переводим младшие единицы времени в его высшие единицы, мы делим.
    • Високосный год — это год, который можно разделить на 4.

      No related posts.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *