ГДЗ за 4 класс по Математике Петерсон Л.Г., Горячева Т.С. самостоятельные и контрольные работы
Описание решебника
авторы: Петерсон Л.Г., Горячева Т.С., Зубавичене Т.В., Невретдинова А.А..
«ГДЗ по математике 4 класс самостоятельные и контрольные работы Петерсон, Горячева (Ювента)» станет незаменимым подспорьем четвероклассникам, желающим овладеть точной наукой на четвёрки и пятёрки. Учебное пособие составлено в соответствии ФГОС. В решебнике ребята смогут отыскать правильные ответы всех номеров заданий основного издания.
По окончании начальной школы учеников ожидает первая в их учебной жизни аттестация по «царице наук» – ВПР. Ребята начинают готовиться заранее, с начала года, и лучшим помощником в учении станет методическое руководство с подробными решениями. С решебником у школьников не возникнет проблем с выполнением домашних заданий – они все смогут решить самостоятельно в команде с компетентным самоучителем.
Положительное участие решебника в освоении предмета
- применение приемов письменного умножения трехзначных чисел на однозначные;
- освоение таблиц единиц площади и массы;
- правило построения прямоугольного треугольника на нелинованной бумаге;
- способы нахождения неизвестного уменьшаемого в решении уравнений.
Регулярные занятия по онлайн-сборнику способствует закреплению пройденного материала, отличным оценкам на уроке и положительным эмоциям от собственных результатов. Ресурс находится в круглосуточном онлайн-доступе. Надежная навигационная система позволит быстро отыскать выбранный номер пособия.
Преимущества правильного использования ГДЗ по математике 4 класс самостоятельные и контрольные работы Петерсон в учебе
К преимуществам применения онлайн-помощника в учёбе можно причислить значительную экономию времени учеников, возможность самостоятельного изучения пропущенных и недостаточно усвоенных разделов, углубление знаний по любой теме и появление уверенных ответов на уроках.
Рекомендуемые решебники
Петерсон Л.Г., Ювента Петерсон Л.Г., Ювента рабочая тетрадь Петерсон Л.Г., БиномОтветы к Выпуску 4.1. Страницы
3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76  2. Страницы «>
Ответы к Выпуску 4.2. Страницы
2. Страницы «>
Ответы к Выпуску 4.2. Страницы
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94Контрольная работа по математике за 1 четверть.
 4 класс. Программа «Перспектива» Л.Г.Петерсон
4 класс. Программа «Перспектива» Л.Г.ПетерсонГлавная / Начальные классы / Математика
Скачать
18.61 КБ, 588380.docx Автор: Афанасьева Наталья Владимировна, 30 Мар 2015
Работа отражает основные темы, которые должны быть усвоены учащимися за 1 четверть.
Автор: Афанасьева Наталья Владимировна
Похожие материалы
| Тип | Название материала | Автор | Опубликован |
|---|---|---|---|
| документ | Контрольная работа по математике за 1 четверть. 4 класс. Программа «Перспектива» Л.Г.Петерсон | Афанасьева Наталья Владимировна | 30 Мар 2015 |
| документ | Контрольная работа по математике за 3 четверть 1 класс УМК «Перспектива» | Гаранина Елена Александровна | 9 Апр 2015 |
| документ | Контрольная работа за 1 четверть 3 класс (Л. Г.Петерсон) Г.Петерсон) | Некрасова Елена Михайловна | 30 Мар 2015 |
| документ | Контрольная работа по математике за 1 четверть 4 класс УМК «Школа России». | Серова Екатерина Юрьевна | 17 Янв 2016 |
| документ | Контрольная работа по математике за первое полугодие. 4 класс. Программа «Перспектива» Л.Г. Петерсон. | Афанасьева Наталья Владимировна | 30 Мар 2015 |
| документ | Контрольная работа по математике за 4 четверть 3 класс | Корниенко Юлия Валентиновна | 30 Мар 2015 |
| документ | Контрольная работа по математике за I четверть 4 класс | Торгашева Тамара Федоровна | 31 Мар 2015 |
| документ | Контрольная работа по математике за III четверть, 4 класс | Гилёва Галина Владимировна | 19 Мар 2016 |
| документ | Контрольная работа по математике 3 класс за 1 четверть | Пухова Ольга Ивановна | 14 Ноя 2015 |
| документ | Контрольная работа по математике за 3 четверть. 1 класс 1 класс | Орлова Галина Александровна | 30 Янв 2016 |
| документ | контрольная работа по математике за 3 четверть 1 класс | Лёвочкина Людмила Леонидовна | 24 Мар 2016 |
| документ | Контрольная работа по математике за 2 четверть 4 класс программа Гармония | Завадская Ольга Николаевна | 5 Апр 2015 |
| документ | Контрольная работа за 3 четверть 2 класс Л.Г.Петерсон | YanaKireeva | 17 Сен 2015 |
| документ | Контрольная работа по математике за I четверть 4 класс УМК «Школа России» | Горбунова Ольга Михайловна | 31 Окт 2015 |
| документ | Контрольная работа по математике за 3 четверть 2 класса (1 вариант). Программа «Гармония», учебник Н.Б. Истоминой Программа «Гармония», учебник Н.Б. Истоминой | Савченко Ирина Фёдоровна | 19 Мар 2016 |
| документ | Контрольная работа по математике за 1 четверть ФГОС 3 класс | Павлунина Татьяна Николаевна | 4 Апр 2015 |
| документ | Контрольная работа по математике за 1 четверть. 3 класс ОС «Школа 2100» | Шимон Светлана Владимировна | 19 Окт 2015 |
| документ | Разноуровневая контрольная работа по математике 3 класс за 1 четверть (УМК «Школа России») | Нефёдова Марина Владимировна | 23 Дек 2015 |
| документ | контрольная работа по математике 1 четверть 4 класс | Бараусова Ольга Владимировна | 30 Мар 2015 |
| разное | Контрольная работа по математике 4 класс (система Занкова Л. В.) 1 четверть В.) 1 четверть | Негадова Ольга Петровна | 30 Мар 2015 |
| документ | Контрольная работа №2 по математике 4 класс 1 четверть | Зубанова Ирина Сергеевна | 30 Июн 2015 |
| документ | Контрольная работа за 1 четверть 4 класс по программе «Школа России» | Кудряшова Татьяна Александровна | 22 Авг 2015 |
| документ | Тематические контрольные работы по математике № 3, № 4, № 5, № 6 ( программа Л.Г. Петерсон, 2 класс). Итоговая контрольная работа по математике за II четверть. | Калиниченко Ольга Викторовна | 5 Апр 2015 |
| документ | Проверочная работа по математике за 1 четверть «Действия с многозначными числами». 4 класс. 4 класс. | Пасечник Светлана Викторовна | 30 Мар 2015 |
| документ | Контрольная работа за 1 четверть УМК «Перспектива» 2 класс | Пашкова Галина Васильевна | 6 Дек 2015 |
| документ | Полезные сведения по математике .4 класс. 1 четверть по учебнику Л.Г.Петерсон | Киргизова Светлана Александровна | 30 Мар 2015 |
| документ | Контрольная работа по математике в 4 классе за 1 четверть 2014 — 2015 учебный год. Школа России. | Кольмай Надежда Ивановна | 30 Мар 2015 |
| документ | Контрольная работа за 1 четверть 4 класс | Мирошник Елена Андреевна | 26 Окт 2015 |
| документ | контрольная работа по математике за 1 четверть | Дерябина Светлана Алексеевна | 30 Мар 2015 |
| документ | Контрольная работа по математике за 1 четверть . | Ломанова Виктория Викторовна | 31 Мар 2015 |
| документ | Контрольная работа по математике за 1 четверть (2 варианта) | Шевчук Виктория Сергеевна | 27 Сен 2015 |
| документ | Итоговая контрольная работа за 1 четверть по математике | Ykusheva | 28 Сен 2015 |
| документ | контрольная работа по математике за 1 четверть | Горынина Екатерина Сергеевна | 16 Окт 2015 |
| документ | Cамостоятельная работа по математике по теме «Измерение углов» 4 класс. Программа Л.Г.Петерсон Программа Л.Г.Петерсон | Масленникова Елена Николаевна | 15 Мар 2016 |
| документ | Контрольная работа по математике за 2 четверть 3 класс | Улякина Татьяна Михайловна | 30 Мар 2015 |
| документ | контрольная работа по математике за 3 четверть 3 класс | Патрогина Елена Владимировна | 30 Мар 2015 |
| разное | Итоговая контрольная работа по математике за 2 четверть 2 класс | Тимохина Валентина Владимировна | 31 Мар 2015 |
| документ | Контрольная работа по математике 3 класс за 3 четверть | Паричук Валентина Васильевна | 12 Апр 2015 |
| документ | Контрольная работа по математике за I четверть, 2 класс | Подшибякина Оксана Алексеевна | 23 Авг 2015 |
| документ | Контрольная работа по математике за 2 четверть 2 класс | Мотина Екатерина Евгеньевна | 9 Фев 2016 |
Входная контрольная работа по математике (4 класс)
В начале учебного года необходимо проверить уровень знаний, чтобы скорректировать дальнейший учебный процесс и определить пробелы в знаниях.
Входная контрольная работа по математике (4 класс)
ФИ учащегося __________________________________________
1. Отметь верную запись числового выражения и его значения.
Разность чисел 532 и 154 умножь на 2.
- (532 — 154) ⋅ 2 = 756
- (532 + 154) ⋅ 2 = 1372
- 532 + 154 ⋅ 2 = 840
- 532 — 154 ⋅ 2 = 224
2. Отметь уравнение, для решения которого нужно из уменьшаемого вычесть разность.
- 700 — х = 234
- х — 700 = 234
- х + 234 = 700
- 234 + х = 700
3. Значение какого выражения равно 0?
- 36 : 6 · 7 : 2 — 11
- 32 : 4 · 5 — 7 · 5
- 6 · 4 : 8 · 0 · 20
- 8 · 2 : 4 · 5 — 10
4. Какое уравнение решается умножением?
- х · 4 = 80
- 4 · х = 80
- х : 4 = 80
- 80 : х = 4
5. Длина прямоугольника 23 см, ширина — 4 см. Найди его периметр.
Найди его периметр.
- 92 см
- 54 см
- 27 см
- 30 см
6. Если 4 одинаковых арбуза весят 48 кг, то сколько весит 1 арбуз?
- 48 · 4 = 198 (кг)
- 48 : 4 = 12 (кг)
- 48 — 4 = 44 (кг)
- 48 + 4 = 52 (кг)
7. В каком выражении знак поставлен неверно?
- 1 кг > 700 г
- 8 дм 7 см = 87 мм
- 89 см < 9 дм
- 65 мин > 1 ч
8. Какая доля самая большая?
- одна третья
- одна десятая
- одна седьмая
- одна четвёртая
9. В каком примере ответ 17?
- 78 : 6
- 120 : 8
- 144 : 9
- 119 : 7
10. Одна десятая часть отрезка равна 20 см. Чему равна длина всего отрезка?
- 2 см
- 30 см
- 10 см
- 200 см
11. Отметь число, в котором 7 единиц первого разряда, 8 единиц второго разряда, 9 единиц третьего разряда.
- 789
- 798
- 987
- 978
12. Отметь, в каком случае число 548 представлено в виде суммы разрядных слагаемых.
- 500 + 48
- 540 + 8
- 510 + 30 + 8
- 500 + 40 + 8
13. Отметь решение, соответствующее задаче.
К празднику приготовили 8 подарков. В каждый подарок положили 6 ирисок и 3 леденца. Сколько всего конфет положили в подарки?
- 8 + 6 + 3 = 17
- 8 · (6 + 3) = 72 (к.)
- 8 · 6 + 8 · 3 = 72 (к.)
- 8 · 6 — 8 · 3 = 28 (к.)
Входная контрольная работа по математике (4 класс)
Ответы
1. Отметь верную запись числового выражения и его значения.
Разность чисел 532 и 154 умножь на 2.
- (532 — 154) ⋅ 2 = 756
- (532 + 154) ⋅ 2 = 1372
- 532 + 154 ⋅ 2 = 840
- 532 — 154 ⋅ 2 = 224
2. Отметь уравнение, для решения которого нужно из уменьшаемого вычесть разность.
- 700 — х = 234
- х — 700 = 234
- х + 234 = 700
- 234 + х = 700
3. Значение какого выражения равно 0?
- 36 : 6 · 7 : 2 — 11
- 32 : 4 · 5 — 7 · 5
- 6 · 4 : 8 · 0 · 20
- 8 · 2 : 4 · 5 — 10
4. Какое уравнение решается умножением?
- х · 4 = 80
- 4 · х = 80
- х : 4 = 80
- 80 : х = 4
5. Длина прямоугольника 23 см, ширина — 4 см. Найди его периметр.
- 92 см
- 54 см
- 27 см
- 30 см
6. Если 4 одинаковых арбуза весят 48 кг, то сколько весит 1 арбуз?
- 48 · 4 = 198 (кг)
- 48 : 4 = 12 (кг)
- 48 — 4 = 44 (кг)
- 48 + 4 = 52 (кг)
7. В каком выражении знак поставлен неверно?
- 1 кг > 700 г
- 8 дм 7 см = 87 мм
- 89 см < 9 дм
- 65 мин > 1 ч
8. Какая доля самая большая?
Какая доля самая большая?
- одна третья
- одна десятая
- одна седьмая
- одна четвёртая
9. В каком примере ответ 17?
- 78 : 6
- 120 : 8
- 144 : 9
- 119 : 7
10. Одна десятая часть отрезка равна 20 см. Чему равна длина всего отрезка?
- 2 см
- 30 см
- 10 см
- 200 см
11. Отметь число, в котором 7 единиц первого разряда, 8 единиц второго разряда, 9 единиц третьего разряда.
- 789
- 798
- 987
- 978
12. Отметь, в каком случае число 548 представлено в виде суммы разрядных слагаемых.
- 500 + 48
- 540 + 8
- 510 + 30 + 8
- 500 + 40 + 8
13. Отметь решение, соответствующее задаче.
К празднику приготовили 8 подарков. В каждый подарок положили 6 ирисок и 3 леденца. Сколько всего конфет положили в подарки?
- 8 + 6 + 3 = 17
- 8 · (6 + 3) = 72 (к.
 )
) - 8 · 6 + 8 · 3 = 72 (к.)
- 8 · 6 — 8 · 3 = 28 (к.)
Центры академической помощи Энтони Петерсона
Все кампусы открыты и готовы обслуживать студентов виртуально, гибридно или лично.
учебной поддержки
студентам и членам сообщества в доброжелательной среде честности, достоинства и творчества. Предлагая профессиональные репетиторские услуги и образовательные ресурсы для
улучшая ключевые навыки, связанные с различными областями контента, центр стремится расширить возможности учащиеся до
становятся независимыми мыслителями, готовыми к успеху в колледже и за его пределами.
 Пожалуйста, выберите ссылку на желаемый кампус ниже, чтобы узнать часы онлайн и специфические для кампуса часы.
и услуги.
Пожалуйста, выберите ссылку на желаемый кампус ниже, чтобы узнать часы онлайн и специфические для кампуса часы.
и услуги. Информационная листовка по бухгалтерскому учету для округа
- Индивидуальная информация о кампусе
- Технический кампус
- Селина
- Фармерсвилл
- Фриско
- Маккинни
- Плано
- Уайли
Для получения дополнительной информации о часах, ресурсах и предметах, которые преподают в каждом кампусе, пожалуйста, нажмите на их имена выше.Для расписания очных и онлайн-встреч в масштабах округа и информацию о предметах и доступности, пожалуйста, выберите предпочитаемый кампус в новой системе расписания Collin APCAA и войдите в систему, используя свой CWID, или отсканируйте свою идентификационную карту Collin College (в центре) для доступа к бесплатному репетиторскому аккаунту.
Ознакомьтесь с нашим руководством по поддержке учащихся округа, чтобы узнать, какую помощь в обучении/репетиторстве предлагает каждый кампус. В кампусе репетиторство по таким предметам, как экономика и бухгалтерский учет, проводится в течение долгих семестров.
Руководство для учащихся по планированию Trac.Cloud
Комната технического кампуса A280
Технический кампус: Часы работы в кампусе
Понедельник — Четверг: 9:00 — 18:00
Пятница: 9:00 — 17:00
Доступна бесплатная печать
Запись на прием в кампусе или онлайн
Математика
4Понедельник — Четверг: 9:00 — 18:00
Пятница: 9:00 — 17:00
Письмо
Понедельник — Четверг: 9:00 — 18:00
Пятница: 9:00 — 17:00
Частные учебные комнаты Открытая компьютерная лаборатория
Микроскоп Check-out : 9:00–13:00 Понедельник-пятница
Руководство по планированию TracCloud
Есть вопросы? 972.
 553.1236
553.1236Напишите нам по адресу [email protected]
Исследовательский вопрос? Спросите библиотекаря
2550 Изгиб ответвления
Allen, TX 75013
Комната A280
Мастерские
Осенние мастерские
Написание ресурсов
Активные и пассивные глаголы
Артикул
Мозговой штурм
Запятые
Выводы по крафту
Создание собственного процесса письма
Оценка источников
Заблуждения
Исправление слитных предложений
Грамматический справочник
Интеграция источников
Введение
MLA Works Цитируется
Стратегии ведения заметок
Пассивный голос
Рецензирование
Точка зрения
Стратегии чтения
Тезисы
Стратегии управления временем
Советы по электронной почте (веб-сайт)
Понимание времен глаголов
Написание профессиональной электронной почты
Информационный бюллетень Celina
Селина Комната 002 (библиотека)
Кампус Celina: часы работы в кампусе
Понедельник — пятница: 9:00 — 17:00
Запись на прием в кампусе или через Интернет
Математика
вторник и четверг: 13:00 — 14:00
Письмо
Понедельник: 10:00 — 16:00
Вторник: 9:30 — 16:00
Среда: с 9:00 до 16:00
Четверг : 9:30 — 16:00
Пятница : 9:00 — 16:00
Биология и АиП :
Понедельник: 10:00 — 17:00
Вторник: 9:00 — 17:00
Есть вопросы? 469. 905.3528
905.3528
Напишите нам по адресу: [email protected]
Исследовательский вопрос? Спросите у библиотекаря
2505 Kinship Parkway
Селина, Техас 75009
Библиотека 002
Мастерские
Осенние мастер-классы: Кампус Селина
Написание ресурсов
Раздаточный материал с цитатами APA
Разработка вопроса исследования
Раздаточный материал с цитатами MLA
Раздаточный материал с цитатами MLA
Фармерсвилл Комната 120
Кампус Farmersville: часы работы в кампусе
Понедельник и среда: 9:00–17:00
Вторник и четверг: 9:00 — 19:00
Доступна бесплатная печать
Запись на прием в кампусе или через Интернет
Математика
Понедельник — Четверг : 9:00 — 19:00
Пятница: 9:00 — 16:00
Письмо
Понедельник и среда: с 9:00 до 16:00
Вторник и четверг: 12:00 — 7:00 вечера.
Пятница: 10:00 — 15:00
Микроскоп Выезд: понедельник — среда и пятница: 8:00 — 17:00
Четверг: 8:00 — 19:00
Электронная почта: [email protected]
Вопросы? 972.549.6499
Исследовательский вопрос? Спросите библиотекаря
501 S. Collin Parkway
Farmersville, TX 75442
Комната 120
6 МастерскиеОсенние семинары скоро
Письменный центр Фриско Комната Lh241
Центр письма во Фриско: Нажмите на эту информационную страницу
Пятница и суббота: 9:00 — 17:00
Доступна бесплатная печать
Запись на прием в кампусе или онлайн-центре письма
Вопросы? 972. 377.1576
377.1576
Пишите нам по адресу: [email protected]
Исследовательский вопрос? Спросите библиотекаря
9700 Wade Blvd.
Фриско, Техас 75035
Математическая лаборатория Фриско F148
Математическая лаборатория Фриско: щелкните эту информационную страницуМатематическая лаборатория в кампусе Фриско: Часы работы в кампусе
Понедельник — четверг: 9:00 — 19:00
Пятница: 9:00 — 17:00
Суббота: 9:00 — 13:00
Доступна бесплатная печать
Назначить встречу в студенческом городке или онлайн-лаборатории по математике и просмотреть расписание
Вопросы? 972.377.1639
Электронная почта: [email protected]
9700 бульвар Уэйд.
Фриско, Техас 75035
Номер Frisco Science Den Lh302
Научный центр кампуса ФрискоПОЖАЛУЙСТА, ОБРАТИТЕ ВНИМАНИЕ: в Science Den можно заходить только по предварительной записи.
Студенты не могут планировать встречи. Для их удобства расписание открыто для всех студентов в поиске помощи науке. Студенты в поисках встреч могут нажать на ссылку ниже для онлайн-встречи или другой доступности встречи в кампусе.
Менеджер научной лаборатории: Мелоди Холмс, [email protected]
Запишитесь на онлайн-встречу в Science Den или проверьте наличие свободных мест. для личной помощи в Frisco
Расписание приема в Science Den с Open Labs
Добро пожаловать
Проверьте расписание приема в Frisco Science Den по предметам и времени.
9700 бульвар Уэйд.
Фриско, Техас 75035
Мастерские
Осенние семинары СкороЦентр письма МакКинни, комната A104
Центр письма
Кампус McKinney: часы работы Центра письма в кампусе
Понедельник — Четверг: 9:00 — 20:00
Пятница: 9:00 — 17:00
Суббота: 12:00 — 5:00 вечера.
Доступна бесплатная печать
Запись на прием в кампусе или онлайн-центре письма
Вопросы? 972-548-6857
Напишите нам по адресу: [email protected]
Исследовательский вопрос? Спросите у библиотекаря
2200 West University Drive
McKinney, Texas 75071
А104
Математическая лаборатория МакКинни, комната C237
Math Lab
McKinney Campus: On Campus Math Lab Часы работы
Понедельник — четверг: 9:00 — 19:00
Пятница: 9:00 — 16:00
Суббота: 10:00 — 13:00
Вопросы? 972-548-6896
Электронная почта: [email protected]
Запишитесь на прием в студенческом городке или в онлайн-лаборатории математики или запишитесь на прием
C237
McKinney Science Den Room LA117
Для получения информации и часов работы звоните в библиотеку МакКинни по телефону: 972-5548-6505
Открыто в часы работы библиотеки для самостоятельного изучения
Научная модель и доступность репетитора/предмета скоро
Эл. Мастерские
Мастерские
Осенние мастерские: кампус McKinney
Plano Room D203
Плано кампус: в кампусе.
Пятница: с 9:00 до 17:00
Суббота: с 11:00 до 17:00
БЕСПЛАТНАЯ ПЕЧАТЬ
Расписание на кампусе или онлайн -встречи
Математика: 0405 — Calculus III
Чтение: Практика критического чтения/Советы
. Написание: Все
.cepan
: Все
667. Химия, органическая химия, физика, биология, анатомия и физиология
Открытая компьютерная лаборатория Микроскопы доступны в часы работы Научные модели
Электронная почта: WCPlano@collin. eduВопрос? 972.881.5843Исследовательский вопрос? Спросите библиотекаря
eduВопрос? 972.881.5843Исследовательский вопрос? Спросите библиотекаря
2800 E. Spring Creek ParkwayPlano, Texas 75074 D203
Plano Rooms D225, D210
D225: Репетиторство по математике
D21. Проверьте листовку ниже.
Workshops
Fall Workshops: Plano Campus
Wylie WLB Suite 217 A — K
Кампус Уайли: Часы работы в кампусе
Понедельник — Четверг: 9:00 — 19:00
Пятница и суббота: с 9:00 до 16:30.
БЕСПЛАТНАЯ ПЕЧАТЬ ПЕЧАТЬ
Списка.0007 Все
Наука: Химия, органическая химия и биология/анатомия и физиология
Открытая компьютерная лаборатория Модели
Заказ микроскопов
Понедельник — четверг: 9:00 — 18:30
Пятница и суббота: с 9:00 до 16:00
Вопрос? 972. 378.8574
378.8574
Электронная почта: [email protected]
Исследовательский вопрос? Спросите библиотекаря
391 Country Club Road
Wylie, Texas 75098
WLB 217 A — K
Семинары
For Prises Workshops: Wylie Campus
9004. Study
Wylie Campus Math and Science Workshops and Online Resources
Как читать и интерпретировать графики
P E M D A S
Точные числа и научные нотации
Значительные рисунки для науки и математики
Row Ops
Линейный программирование
GAUSS Jordan
. Онлайн-ресурсы по математике
Бесплатный графический калькулятор
Веб-сайты по общей математике и математическим упражнениям
Академия Хана: Основы алгебры
Академия Хана: Precalculus
Академия Хана: Статистика
PurpleMath.com: Практический курс TSI по математике
Образцы математических задач TSI II для практики
QuickTips Science Workshops/PDFs/Links to Apps Atlas
4 Atlas Body
Бесплатные практические тесты HESI
Бесплатные практические тесты TEAS
Бесплатные практические тесты TSI
Что такое гипотеза? (PDF)
Важные цифры
UCONN: Письмо в биологии
Umanitoba: написание отчета о научной лаборатории (PDF)
Семинары по написанию быстрого питания/PDFS
Статьи (PDF)
Стратегии для критического чтения (PDF)
больше стратегий чтения
. (PDF для слабослышащих)
(PDF для слабослышащих)
Ссылки на правительственные документы и веб-сайты
Прямое цитирование и ссылки на источники
Вступление в беседу: Исследования для аргументации Эссе
Вступление в беседу: (PDF для слабослышащих)
Боковой поиск: как оценить достоверность источников в Интернете
MLA PowerPoint/8th Edition
Перефразирование источников
Советы по более эффективному письму
Онлайн-ресурсы900s и игры
Purdue OWL: APA Style Introduction
Chicago Manual of Style Online
Grammar Bytes!
Бесплатное сопоставление слов о рисе (предлагается Всемирной продовольственной программой ООН)
Центр стиля MLA: как оформить исследовательскую работу
Онлайн-репетиторство
Запись на прием онлайн или в кампусе
Вопрос?
Эл.
продолжительностью один час. Студенты ACCESS должны отправить запрос и подтверждение размещения ACCESS.
по адресу [email protected]. Пожалуйста, укажите свое имя в теле письма и сообщите нам, что вы запрашиваете
увеличенное время обучения.
Студенты ACCESS должны отправить запрос и подтверждение размещения ACCESS.
по адресу [email protected]. Пожалуйста, укажите свое имя в теле письма и сообщите нам, что вы запрашиваете
увеличенное время обучения.
Онлайн-семинары
Скоро вскоре
Район по всему окружному расписанию по математике
для мест, предметов и времени, пожалуйста, скачайте этот PDF
или перейдите в этот онлайн -расписание
Fast Wist inrw Grade
4 400464. , темы и время, пожалуйста, загрузите ЭТОТ PDF-файл
или перейдите к ЭТОМУ онлайн-планировщику встреч
Нарушение исполнительной функции и математика
Эван — симпатичный ученик четвертого класса, у которого много друзей, но у него проблемы в школе, особенно с математикой. В прошлом году ему поставили диагноз СДВГ из-за его поведения, связанного с концентрацией внимания. Эван думает, что понимает материал, но дома с трудом выполняет домашнюю работу. Больше всего он чувствует себя побежденным, когда проходит тесты по главам и модульные тесты, где ему трудно понять, с чего начать различные многошаговые задачи. Во многих задачах ответы Эвана выглядят как догадки, а не как результат систематического подхода к решению проблем. Эван разочарован работой и потерял мотивацию. Учитель говорит ему, что он мог бы выполнить работу, если бы просто приложил больше усилий.
В прошлом году ему поставили диагноз СДВГ из-за его поведения, связанного с концентрацией внимания. Эван думает, что понимает материал, но дома с трудом выполняет домашнюю работу. Больше всего он чувствует себя побежденным, когда проходит тесты по главам и модульные тесты, где ему трудно понять, с чего начать различные многошаговые задачи. Во многих задачах ответы Эвана выглядят как догадки, а не как результат систематического подхода к решению проблем. Эван разочарован работой и потерял мотивацию. Учитель говорит ему, что он мог бы выполнить работу, если бы просто приложил больше усилий.
То, что происходит с Эваном, мало чем отличается от того, что происходит со многими учениками с СДВГ. Эван хочет хорошо успевать по математике, но испытывает трудности с многоэтапным решением задач и переходом от одного типа задач к другому. Хотя он хочет добиться успеха, его более низкая успеваемость заставила его устать от попыток улучшить, что привело к отсутствию усилий в математике. Эти характеристики указывают на проблемы с исполнительным функционированием (EF).
Эти характеристики указывают на проблемы с исполнительным функционированием (EF).
Исследователи Рассел Баркли, Кевин Мерфи и Мариеллен Фишер обнаружили, что у учащихся с СДВГ часто возникают проблемы с исполнительными функциями. EF ученика проявляется в том, как он регулирует свое собственное учебное поведение, что имеет решающее значение для успеха в нескольких аспектах жизни, включая изучение математики (Clements et al., 2016). Как правило, УФ включает три компонента: саморегуляцию, рабочую память и восстановление. Каждая из этих областей влияет друг на друга.
Саморегуляция Саморегуляция проявляется как импульсивность в подходе к решению проблем. Это может проявиться, когда математика показана как серия быстрых трюков, содержание которых не понимается до того, как будет вычислен ответ. Для Эвана это особенно хлопотно. В четвертом классе математика становится все более сложной, особенно с текстовыми задачами. В этой задаче (EngageNY, 2019, стр. 10) Эван должен проанализировать текстовую задачу, разработать точный подход и вычислить ответ:
10) Эван должен проанализировать текстовую задачу, разработать точный подход и вычислить ответ:
Мистер Фуллер хочет поставить забор вокруг своего прямоугольного двора. Ширина двора 55 футов, а длина 75 футов. Сколько футов ограждения нужно мистеру Фуллеру?
- 130
- 260
- 3 905
- 4 125
Если Эвану не хватает саморегуляции, чтобы прочитать и проанализировать задачу, он может увидеть компоненты словесной задачи 55 футов и 75 футов, а также увидеть, что ответом является вопрос о футах. Итак, используя свою относительную вычислительную мощь, он просто прибавляет 55 + 75, чтобы получить 130. Рассматривая 130 как первый вариант ответа, A , он уверен, что прав. В конце концов, то, что он вычислил, сначала проявляется в вариантах ответов. В этой задаче Эвану не удается интерпретировать проблему как решение для периметра из-за его импульсивности в процессе решения проблемы.
Чтобы помочь таким учащимся, как Эван, предоставьте пошаговые инструкции по решению проблем. Хотя было показано, что многие подходы помогают, даже трехступенчатая когнитивная стратегия (Скажи, Спроси, Проверь) улучшит решение задач учащимися и поможет развить саморегуляцию (Монтегю, 2008).
| Произнесите | Эван читает задачу, спрашивая себя, понимает ли он представленную информацию. |
| Спросите | Эван строит внутренний диалог, задавая себе вопросы по поводу информации, например: «Что задает вопрос?» и «Как мне использовать информацию в задаче, чтобы ответить на вопрос?» Эван может даже перефразировать слово «проблема», чтобы увидеть, представлена ли информация в понятной ему манере. |
| Чек | Эван сравнивает свой ответ с заданным вопросом. |
Эта когнитивная стратегия поможет Эвану научиться саморегуляции при решении проблемы, чтобы он отвечал на нее обдуманно, а не импульсивно.
Рабочая память демонстрируется путем хранения информации при обработке события, так что информация сохраняется и может быть эффективно обработана и вызвана для использования в подходящее время (Witzel, 2016). Различные компоненты рабочей памяти служат предикторами математических рассуждений учащегося (Meyer, 2010). В частности, зрительно-пространственная рабочая память (VSWM) влияет на подходы учащихся к решению арифметических задач (Ashkenazi, 2013) и общую успеваемость по математике (Allen, 2019).). VSWM похож на блокнот, где учащиеся могут мысленно представлять числа и арифметику, например, на числовой прямой или с помощью модели области. Слишком часто учащиеся с трудностями в математике не используют ВСМ при решении арифметических задач (Ашкенази, 2013). Таким образом, важно помочь учащимся построить ментальные образы математики, чтобы помочь учащимся развить VSWM.
Хотя использование когнитивных стратегий помогает учащимся решать математические задачи, включение визуальных представлений улучшает успеваемость учащихся (Swanson, 2015). В том же примере с периметром, показанном ранее, Эвану нужно предложить нарисовать визуальное представление, которое будет отображать событие решения проблемы, чтобы помочь его VSWM.
В том же примере с периметром, показанном ранее, Эвану нужно предложить нарисовать визуальное представление, которое будет отображать событие решения проблемы, чтобы помочь его VSWM.
На этапе Спросить Эван должен нарисовать визуальное представление, чтобы помочь построить внутренний диалог.
| 75 футов | |
| 55 футов |
Это визуальное представление поможет ему изучить различные параметры, с которыми он, возможно, уже знаком (например, периметр и площадь). Задавая себе вопрос о том, что задает проблема, он настраивает свое визуальное представление, чтобы легче представить периметр забора.
| 75 футов | ||
| 55 футов | 55 футов | |
| 75 футов |
Во время проверки в рамках когнитивной стратегии он сравнивает свой рисунок со своим ответом в 260 футов, помогая ему увидеть связь между проблемой и его подходом.
Восстановление — это способность переключать внимание с одной конструкции на другую и приспосабливаться к новым требованиям. Джосвик и коллеги (2019 г.) подчеркнул важность помощи учащимся научиться переключаться с одной задачи на другую и найти подходящую и эффективную стратегию для решения новой задачи.
Эван только что решил задачу, требующую понимания и вычисления периметра. Поэтому он будет склонен решать за периметром подобные задачи. Возьмем, к примеру, эту проблему со словом (EngageNY, 2019, стр. 11):
Мисс Петерсон хочет заменить всю напольную плитку на своей кухне. Пол кухни 12 футов в длину и 7 футов в ширину. Если у г-жи Петерсон уже есть 45 квадратных плиток в один фут, сколько еще плиток в один фут ей нужно, чтобы полностью покрыть кухонный пол?
Вместо этого Эвану нужно перезапустить свою когнитивную стратегию. Это может быть сложно для ученика, который борется с EF. Чтобы помочь учащемуся переключаться с задачи на задачу, рассмотрите возможность предоставления органайзера подсказок для запуска задач. В этом примере учитель дает Эвану органайзер с подсказками, которые соответствуют его когнитивной стратегии решения проблем, и Эван заполняет пробелы, чтобы начать. В этом примере учитель также выделяет жирным шрифтом подсказку, чтобы указать Эвану, что делать.
В этом примере учитель дает Эвану органайзер с подсказками, которые соответствуют его когнитивной стратегии решения проблем, и Эван заполняет пробелы, чтобы начать. В этом примере учитель также выделяет жирным шрифтом подсказку, чтобы указать Эвану, что делать.
| В чем проблема? | Сколько квадратных плиток размером в один фут еще нужно? | ||||||||||
| Что уже дано? | Длина | 12 футов | |||||||||
| Ширина | 7 футов | ||||||||||
| Квадратные плитки, которые у нее уже есть | 45 | ||||||||||
| Нарисуйте визуализацию, соответствующую задаче |
| ||||||||||
Нам нужно найти площадь. Почему? | Мне нужно знать размер всего этажа | ||||||||||
| Тогда что нам делать? Почему? | Я вычитаю количество плиток, которые у нее уже есть. Это позволяет мне узнать, сколько еще плиток ей нужно. | ||||||||||
| Область расчета 12 футов x 7ft = 84ft 2 84 фута 2 — 45 футов 2 = 39 -футовую 2 все еще необходимы. Мисс Петерсон все еще нужно 39 плиток. | |||||||||||
Предоставляя органайзер подсказок, Эван может видеть, что ему нужно для решения проблемы. Он завершает каждый шаг в органайзере, прежде чем начнет свой расчет. Это не только помогает ему более эффективно переключаться с задачи на задачу, но также дает ему сигналы для саморегуляции и визуальной рабочей памяти. По мере того как Эван привыкает к переключению задач, учитель будет сокращать количество подсказок, чтобы со временем и успехом Эван стал более независимым.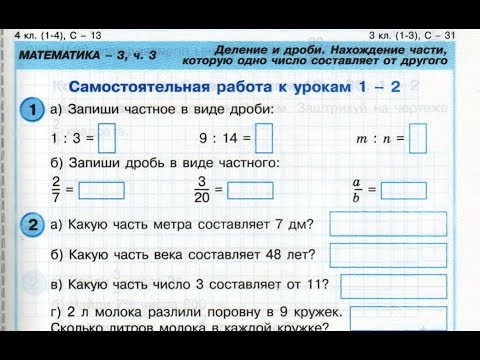
Для решения исполнительных функций в математике требуется тщательное планирование и реализация стратегии, чтобы не только удовлетворить потребности учащегося, но и использовать сильные стороны учащегося. В примере с Эваном учитель включил когнитивную стратегию, визуальное представление и организатор подсказок.
Существует множество других способов помочь учащимся с дефицитом УФ, например, сосредоточить внимание на автоматизме операционных фактов, чтобы уменьшить будущую когнитивную нагрузку, и использовать позитивный поведенческий подход для поощрения усилий. Борьба с исполнительными функциями не обязательно должна останавливать процесс обучения математике. Скорее, это призыв к более эффективным стратегиям.
Брэдли Витцель, доктор философии , отмеченный наградами преподаватель и почетный профессор педагогики Аделаиды Уорт Дэниелс в Университете Западной Каролины.
 В качестве классного руководителя, а до этого в качестве помощника преподавателя, он работал в различных условиях, обучая в основном математике и естественным наукам хорошо успевающих учащихся с ограниченными возможностями. Доктор Витцель написал множество книг, глав в книгах и учебных пособий, а также несколько десятков научных и практических статей. Он разработал и представил шесть образовательных видеороликов и провел более 500 семинаров и презентаций на конференциях. Самое главное, он отец двоих детей, муж педагога и сын двух педагогов.
В качестве классного руководителя, а до этого в качестве помощника преподавателя, он работал в различных условиях, обучая в основном математике и естественным наукам хорошо успевающих учащихся с ограниченными возможностями. Доктор Витцель написал множество книг, глав в книгах и учебных пособий, а также несколько десятков научных и практических статей. Он разработал и представил шесть образовательных видеороликов и провел более 500 семинаров и презентаций на конференциях. Самое главное, он отец двоих детей, муж педагога и сын двух педагогов. ССЫЛКИ И ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
Аллен, К., Хиггинс, С. и Адамс, Дж. (2013). Связь между зрительно-пространственной рабочей памятью и математическими способностями у детей школьного возраста: систематический обзор.
Educational Psychology Review, 31, 509–531. https://doi.org/10.1007/s10648-019-09470-8Ашкенази С., Розенберг-Ли М., Меткалф А.В.С., Свигарт А.
 Г. и Менон В. (2013). Зрительно-пространственная рабочая память является важным источником общей уязвимости домена в развитии арифметического познания. Нейропсихология, 51 (11), 2305-2317.
Г. и Менон В. (2013). Зрительно-пространственная рабочая память является важным источником общей уязвимости домена в развитии арифметического познания. Нейропсихология, 51 (11), 2305-2317.Баркли, Р.А., Мерфи, К.Р., и Фишер, М. (2008).
СДВГ у взрослых: что говорит наука. Нью-Йорк: Гилфорд Пресс. Клементс, Д.Х., Сарама, Дж., и Гермерот, К. (2016). Обучение исполнительной функции и ранняя математика: Направления причинно-следственных связей. Early Ежеквартальное исследование детства, 36(3), 79–90. заниматьсяNY. (2019, июнь). Программа тестирования штата Нью-Йорк. 4 класс. Тест по математике. Выпущенные вопросы. Доступно по адресу https://www.engageny.org/resource/released-2019.-3-8-ela-and-mathematics-state-test-questionsДжосвик, К., Клементс, Д.Х., Сарама, Дж., Банс, Х.В., и Дэй-Хесс, К.А. (2019). Двойное воздействие: математика и исполнительная функция.
Обучение детей математике, 25 (7), 416-426.Монтегю, М.
 (2008 г.). Стратегии саморегуляции для улучшения решения математических задач для учащихся с ограниченными возможностями обучения. Ежеквартальный отчет по нарушению обучаемости, 31 , 37–44.
(2008 г.). Стратегии саморегуляции для улучшения решения математических задач для учащихся с ограниченными возможностями обучения. Ежеквартальный отчет по нарушению обучаемости, 31 , 37–44.Swanson, HL, Lussier, CM, & Orosco, MJ (2015). Когнитивные стратегии, рабочая память и рост в решении словесных задач у детей с математическими трудностями.
Journal of Learning Disability, 48 (4), 339-358.Witzel, BS, & Little, ME (2016).
Преподавание элементарной математики отстающим ученикам. Нью-Йорк: Гилфорд Пресс.Чартерные школы демонстрируют более крутую тенденцию к росту успеваемости учащихся, чем окружные школы
Число чартерных школ быстро росло в течение четверти века после того, как первая чартерная школа открыла свои двери в 1992 году. Но с 2016 года темпы роста замедлились. Связана ли пауза со снижением эффективности устава?
Чтобы выяснить это, мы отслеживаем изменения в успеваемости учащихся в чартерных и окружных школах с помощью Национальной оценки успеваемости, которая проверяет навыки чтения и математики репрезентативной для страны выборки учащихся раз в два года. Мы фокусируемся на тенденциях успеваемости учащихся с 2005 по 2017 год, чтобы понять, в каком направлении движется округ и чартерный сектор. Мы также контролируем различия в фоновых характеристиках учащихся. Это первое исследование, в котором эта информация используется для сравнения линий тренда. В большинстве предыдущих исследований сравнивалась относительная эффективность чартерного и окружного секторов в один момент времени.
Мы фокусируемся на тенденциях успеваемости учащихся с 2005 по 2017 год, чтобы понять, в каком направлении движется округ и чартерный сектор. Мы также контролируем различия в фоновых характеристиках учащихся. Это первое исследование, в котором эта информация используется для сравнения линий тренда. В большинстве предыдущих исследований сравнивалась относительная эффективность чартерного и окружного секторов в один момент времени.
Наш анализ показывает, что когорты студентов в чартерном секторе добились большего прироста с 2005 по 2017 год, чем когорты в районном секторе. Разница в тенденциях в двух секторах составляет почти дополнительное полугодовое обучение. Самые большие успехи имеют афроамериканцы и учащиеся с низким социально-экономическим статусом, посещающие чартерные школы. Когда мы делаем поправку на изменения в характеристиках студенческого образования, мы обнаруживаем, что две трети относительного прироста в чартерном секторе не могут быть объяснены демографией. Другими словами, скорость изменений выше либо потому, что чартерный сектор, по сравнению с районным, привлекает более квалифицированных учащихся способами, которые невозможно определить по демографическим характеристикам, либо потому, что чартерные школы и их учителя лучшая работа по обучению студентов.
Три десятилетия роста
Первая в стране чартерная школа открылась в Миннесоте в 1991 году в соответствии с законом штата, который установил новый тип независимой школы, финансируемой государством. Школьные системы в 43 штатах и округе Колумбия теперь включают чартерные школы, а в таких штатах, как Калифорния, Аризона, Флорида и Луизиана, их посещает более одного из 10 учащихся государственных школ. В некоторых крупных городах эти цифры еще больше: 45 % в Вашингтоне, округ Колумбия, 37 % в Филадельфии и 15 % в Лос-Анджелесе.
В период с 2005 по 2017 год количество чартерных учащихся по всей стране увеличилось в три раза, при этом число чартерных учащихся выросло с 2 до 6 процентов от всех учащихся государственных школ. Но темпы роста замедлились после 2016 г. (см. «Почему рост чартерных компаний замедляется? Уроки залива», исследование , , лето 2018 г.). Этому есть несколько возможных причин. Количество штатов, принимающих хартийные законы, снизилось после 1999 года, и многие из законов, принятых после 2000 года, включали положения, которые могут затормозить рост: ограничения на количество разрешенных школ, таинственные требования к заявлениям, землепользование и другие правила. Кроме того, политическая реакция замедляет расширение чартерных услуг в некоторых штатах.
Кроме того, политическая реакция замедляет расширение чартерных услуг в некоторых штатах.
Исследователи, изучавшие успеваемость учащихся чартерных и окружных школ в один и тот же момент времени, в целом обнаружили, что она очень похожа. Например, в отчете Национального центра статистики образования «Выбор школы в США» за 2019 год были рассмотрены результаты тестов учащихся по чтению и математике в 2017 году и не было обнаружено «измеримых различий» между секторами. Кроме того, исследования Центра исследований результатов образования (CREDO) в Стэнфордском университете, проведенные в нескольких штатах, выявили лишь небольшие различия в успеваемости в чартерных и окружных школах.
Анализы, обобщающие результаты нескольких исследований, также указывают на небольшую разницу в среднем между двумя секторами, хотя и определяют конкретные ситуации, в которых чартерные школы преуспевают. Во всестороннем обзоре, опубликованном в 2018 году, Сара Коходс написала, что, хотя данные в целом показывают «в среднем нет разницы» между двумя секторами, «городские чартерные школы, обслуживающие учащихся из числа меньшинств и малоимущих, которые используют принцип «без оправданий» учебная программа» имеют «значительное положительное влияние». В 2019 годуметаанализ 47 чартерных исследований, Джулиан Беттс и Ю. Эмили Танг обнаружили, что в целом лишь небольшой прогнозируемый выигрыш от посещения чартера составляет от половины до одного процентиля. А в статье 2020 года Анна Эгалите сообщила о небольшой разнице в среднем между двумя секторами, но написала, что хартии в некоторых регионах показывают «статистически значимый, большой и значимый с точки зрения образования прирост успеваемости» для учащихся с низким доходом, цветных учащихся и школьников. Изучающие английский язык.
В 2019 годуметаанализ 47 чартерных исследований, Джулиан Беттс и Ю. Эмили Танг обнаружили, что в целом лишь небольшой прогнозируемый выигрыш от посещения чартера составляет от половины до одного процентиля. А в статье 2020 года Анна Эгалите сообщила о небольшой разнице в среднем между двумя секторами, но написала, что хартии в некоторых регионах показывают «статистически значимый, большой и значимый с точки зрения образования прирост успеваемости» для учащихся с низким доходом, цветных учащихся и школьников. Изучающие английский язык.
Однако ни в одном исследовании не использовались данные, репрезентативные для страны, с контролем фоновых характеристик для оценки тенденций в успеваемости учащихся за двенадцатилетний период. Это наша цель здесь.
Данные и метод
Наши данные взяты из Национальной оценки прогресса в образовании. NAEP — это тест с низкими ставками, который не определяет успеваемость какого-либо учащегося, учителя, школы или школьного округа. Скорее, он используется для оценки общего уровня знаний учащихся государственных школ страны по различным предметам на уровне штата и страны. Репрезентативная по стране выборка учащихся 4, 8 и 12 классов сдает тесты по чтению и математике раз в два года. Мы не сообщаем результаты для учащихся 12-х классов, потому что количество тестовых наблюдений в чартерном секторе слишком мало, чтобы можно было провести точную оценку.
Скорее, он используется для оценки общего уровня знаний учащихся государственных школ страны по различным предметам на уровне штата и страны. Репрезентативная по стране выборка учащихся 4, 8 и 12 классов сдает тесты по чтению и математике раз в два года. Мы не сообщаем результаты для учащихся 12-х классов, потому что количество тестовых наблюдений в чартерном секторе слишком мало, чтобы можно было провести точную оценку.
В период с 2005 по 2017 год учащимся округа было проведено более четырех миллионов тестов, и почти 140 000 тестов было проведено учащимся чартерных школ, при этом доступны данные об этнической принадлежности каждого учащегося, его поле, праве на бесплатный или льготный обед, а для восьмого- только учащиеся класса, уровень образования родителей, количество книг в доме и наличие компьютера в доме. Мы не включаем в наш основной анализ средства контроля за участием в программах специального образования и обучения английскому языку, финансируемых из федерального бюджета, потому что школы в этих двух секторах могут по-разному определять право на участие. Однако мы подтверждаем, что наши результаты не меняются существенным образом при введении контроля для этих двух переменных.
Однако мы подтверждаем, что наши результаты не меняются существенным образом при введении контроля для этих двух переменных.
Мы сообщаем о тенденциях стандартных отклонений, что является традиционным способом описания различий в производительности стандартизированных тестов. Поскольку тесты NAEP связаны подмножествами вопросов, заданных как в 4-м, так и в 8-м классе, мы можем использовать этот показатель для оценки разницы в средних показателях учащихся этих классов. Затем мы создаем оценку стоимости обучения за год на основе средней разницы в успеваемости учащихся между этими классами.
Мы сравниваем результаты когорт учащихся в этих тестах в 2005 и 2017 годах и обнаруживаем, что в среднем учащиеся 8-го класса показали на 1,23 стандартного отклонения больше, чем учащиеся 4-го класса. Это означает, что учащиеся каждый год узнают достаточно, чтобы повысить свои результаты тестов по чтению и математике примерно на 0,31 стандартного отклонения. Соответственно, мы интерпретируем улучшение результатов теста на 0,31 стандартного отклонения как эквивалент примерно одного года обучения.
Тенденции успеваемости основаны на разнице между баллами уставных и окружных школ по тестам NAEP в 2007, 2009, 2011, 2013, 2015 и 2017 годах и их средними баллами в 2005 году, которые установлены равными нулю. Мы сообщаем об этих различиях в стандартных отклонениях. Мы применяем весовые коэффициенты опроса, предоставленные NAEP, для получения репрезентативных результатов.
Изучение различий по типам школ
Сначала мы рассмотрим разницу в средних баллах по тестам 2005 и 2017 годов. В среднем районные школы превзошли чартерные школы в 2005 году как в 4-х, так и в 8-х классах, особенно по математике. Для учащихся 4-х классов средний балл по математике в окружных школах составил 237 баллов по сравнению с 232 баллами в чартерных школах, что составляет разницу в 0,15 стандартных отклонения. По чтению средний балл округа составлял 217 баллов по сравнению с 216 баллами в чартерных школах. Для учащихся 8-х классов средний балл по математике в окружных школах составлял 278 по сравнению с 268 в чартерных школах, разница составляет около 0,28 стандартных отклонений. По чтению средний балл округа составлял 260 баллов по сравнению с 255 баллами в чартерных школах.
По чтению средний балл округа составлял 260 баллов по сравнению с 255 баллами в чартерных школах.
К 2017 году большинство этих различий исчезли или почти исчезли (см. рис. 1). В 4-м классе чартеры по-прежнему отставали от округов на 3 балла по математике со средним баллом 236 по сравнению с 239. Однако по чтению средний балл чартеров был на один балл выше — 266 по сравнению с 265 для районных школ. На тестах 8-го класса сектор имел одинаковый средний балл по математике 282 и практически такой же по чтению: 266 для чартерных и 265 для районных школ. Ни одно из этих различий 2017 года не было достаточно большим, чтобы быть статистически значимым.
Рассматривая тенденции успеваемости по всем семи тестам NAEP по математике и чтению с 2005 по 2017 год, мы обнаруживаем более значительный рост успеваемости учащихся чартерных школ, чем учащихся районных школ (см. рис. 2). В среднем по классам и предметам результаты тестов в чартерных школах за это время улучшились на 0,24 стандартного отклонения по сравнению с 0,1 стандартным отклонением в окружных школах.

 2. Страницы «>
Ответы к Выпуску 4.2. Страницы
2. Страницы «>
Ответы к Выпуску 4.2. Страницы )
) Для расписания очных и онлайн-встреч в масштабах округа
и информацию о предметах и доступности, пожалуйста, выберите предпочитаемый кампус
в новой системе расписания Collin APCAA и войдите в систему, используя свой CWID, или отсканируйте свою идентификационную карту Collin College (в центре)
для доступа к бесплатному репетиторскому аккаунту.
Для расписания очных и онлайн-встреч в масштабах округа
и информацию о предметах и доступности, пожалуйста, выберите предпочитаемый кампус
в новой системе расписания Collin APCAA и войдите в систему, используя свой CWID, или отсканируйте свою идентификационную карту Collin College (в центре)
для доступа к бесплатному репетиторскому аккаунту.
 Студенты не могут планировать
встречи. Для их удобства расписание открыто для всех студентов в поиске
помощи науке. Студенты в поисках встреч могут нажать на ссылку ниже
для онлайн-встречи или другой доступности встречи в кампусе.
Студенты не могут планировать
встречи. Для их удобства расписание открыто для всех студентов в поиске
помощи науке. Студенты в поисках встреч могут нажать на ссылку ниже
для онлайн-встречи или другой доступности встречи в кампусе.