Демоверсия ВПР 2023 по математике для 4 класса
Официальная демоверсия проверочной работы по математике для 4 класса.
ВПР в 2023 году пройдут с 15 марта по 20 мая. Точные даты устанавливает образовательная организация самостоятельно.
Всего в работе 12 заданий. Время выполнения — 45 минут.
При выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором.
→ Демоверсия: vpr_ma-4_demo_2023.pdf
→ Описание работы: vpr_ma-4_opisanie_2023.pdf
Цитата: Система оценивания
Каждое верно выполненное задание 1, 2, 4, 5 (пункт 1), 5 (пункт 2), 6 (пункт 1), 6 (пункт 2), 7, 9 (пункт 1), 9 (пункт 2) оценивается 1 баллом. Задание считается выполненным верно, если ученик дал верный ответ: записал правильное число, правильную величину, изобразил правильный рисунок.
Выполнение каждого из заданий 3, 8, 10–12 оценивается от 0 до 2 баллов.
Максимальный первичный балл за выполнение работы — 20.
Перевод баллов в оценку:
«2»: 0–5
«3»: 6–9
«4»: 10–14
«5»: 15–20
Описание ВПР по математике
В заданиях 1, 2, 7 проверяется умение выполнять арифметические действия с числами и числовыми выражениями. В частности, задание 1 проверяет умение выполнять сложение, вычитание, умножение и деление однозначных, двузначных и трехзначных чисел в случаях, сводимых к действиям в пределах 100 (в том числе с нулем и числом 1). Задание 2 проверяет умение вычислять значение числового выражения, соблюдая при этом порядок действий. Заданием 7 контролируется умение выполнять письменно действия с многозначными числами (сложение, вычитание, умножение и деление на однозначное, двузначное числа в пределах 10 000).
Выполнение заданий 3 и 8 предполагает использование начальных математических знаний для описания и объяснения окружающих предметов, процессов, явлений, для оценки количественных и пространственных отношений предметов, процессов, явлений.
Задание 4 выявляет умение читать, записывать и сравнивать величины (время), используя основные единицы измерения величин и соотношения между ними.
Умение решать текстовые задачи в три-четыре действия проверяется заданием 8. При этом в задании 8 необходимо выполнить действия, связанные с использованием основных единиц измерения величин (длина, вес).
Умение исследовать, распознавать и изображать геометрические фигуры проверяется заданием 5. Пункт 1 задания предполагает вычисление периметра прямоугольника и квадрата, площади прямоугольника и квадрата. Пункт 2 задания связан с построением геометрических фигур с заданными измерениями (отрезок, квадрат, прямоугольник) с помощью линейки, угольника.
В задании 6 проверяется умение работать с таблицами, схемами, графиками, диаграммами, анализировать и интерпретировать данные.
Задание предполагает чтение и анализ несложных готовых таблиц. Овладение основами логического и алгоритмического мышления контролируется заданиями 9 и 12. Задание 9 связано с интерпретацией информации (объяснять, сравнивать и обобщать данные, делать выводы и прогнозы). Задание 12 требует умения решать текстовые задачи в три-четыре действия.
Задание 10 проверяет умение извлекать и интерпретировать информацию, представленную в виде текста, строить связи между объектами.
Овладение основами пространственного воображения выявляется заданием 11. Оно предполагает описание взаимного расположения предметов в пространстве и на плоскости.
Успешное выполнение обучающимися заданий 10–12 в совокупности с высокими результатами по остальным заданиям говорит о целесообразности построения для них индивидуальных образовательных траекторий в целях развития их математических способностей.
Journal of Algebra Combinatorics Discrete Structures and Applications » Заявка » Об одном классе одночленноподобных абелевых кодов с повторными корнями
Подробнее
| Основной язык | Английский |
|---|---|
| Субъекты | Инжиниринг |
| Раздел журнала | Артикул |
| Авторы | Эдгар Мартинес-Моро Это я Хакан Озадам Это я Феррух Озбудак Это я Стив Сабо Это я |
| Дата публикации | 30 апреля 2015 г. |
| Опубликовано в выпуске | 2015 год, Том 2, Выпуск 2 |
Укажите
| Бибтекс | @исследовательская статья { jacodesmath268447,
journal = {Журнал комбинаторики дискретных структур и приложений алгебры},
эйссн = {2148-838X},
адрес = {},
издатель = {Ирфан ШИАП},
год = {2015},
громкость = {2},
число = {2},
страницы = {75 — 84},
дои = {10. 13069/jacodesmath.17537},
title = {Об одном классе мономиальноподобных абелевых кодов с кратными корнями},
ключ = {цитировать},
автор = {Мартинес-моро, Эдгар и Озадам, Хакан и Озбудак, Феррух и Сабо, Стив}
} |
| АПА | Мартинес-моро, Э.
, Озадам, Х.
, Озбудак, Ф.
и Сабо, С.
(2015). |
| ГНД | Мартинес-моро, Э.
, Озадам, Х.
, Озбудак, Ф. , Сабо, С.
«Об одном классе мономиальноподобных абелевых кодов с кратными корнями»
.
Журнал комбинаторики алгебры, дискретные структуры и приложения 2 (2015 г.)
): 75-84 |
| Чикаго | Мартинес-моро, Э. , Озадам, Х.
, Озбудак, Ф.
, Сабо, С.
«Об одном классе мономиальноподобных абелевых кодов с кратными корнями».
Журнал комбинаторики алгебры, дискретные структуры и приложения 2 (2015 г.)
): 75-84 |
| РИС | ТЫ — ДЖУР
T1 — Об одном классе мономиальноподобных абелевых кодов с кратными корнями
AU — Эдгар Мартинес-моро, Хакан Озадам, Феррух Озбудак, Стив Сабо
1 год – 2015 г.
ПГ — 2015
N1 — doi: 10.13069/jacodesmath.17537 DO — 10. 13069/jacodesmath.17537 T2 — Журнал комбинаторики алгебры Дискретные структуры и приложения
JF — Журнал
ДЖО — ДЖОР
СП — 75
ЭП — 84
ВЛ — 2
ИС — 2
Серийный номер — -2148-838X
M3 — дои: 10.13069/jacodesmath.17537 UR — https://doi.org/10.13069/jacodesmath.17537 Y2 — 2023
Скорая помощь — |
| Примечание | %0 Journal of Algebra Combinatorics Дискретные структуры и приложения Об одном классе мономиальноподобных абелевых кодов с кратными корнями
%A Эдгар Мартинес-моро
, Хакан Озадам
, Феррух Озбудак
, Стив Сабо
%T Об одном классе мономиальноподобных абелевых кодов с кратными корнями
%D 2015
%J Журнал комбинаторики алгебры Дискретные структуры и приложения
%P-2148-838X
%V 2
%N 2
%R дои: 10. 13069/jacodesmath.17537 %U 10.13069/jacodesmath.17537 |
| ИСНАД | Мартинес-моро, Эдгар
, Озадам, Хакан
, Озбудак, Феррух
, Сабо, Стив
.
«Об одном классе мономиальноподобных абелевых кодов с кратными корнями».
Журнал комбинаторики алгебры Дискретные структуры и приложения
2
/
2
(апрель 2015 г. ):
75-84
. https://doi.org/10.13069/jacodesmath.17537 |
| АМА | Мартинес-моро Э.
, Озадам Х.
, Озбудак Ф.
, Сабо С.
Об одном классе мономиальноподобных абелевых кодов с кратными корнями.
Журнал комбинаторики алгебры, дискретных структур и приложений.
2015 г. ;
2(2):
75-84. |
| Ванкувер | Мартинес-моро Э.
, Озадам Х.
, Озбудак Ф.
, Сабо С.
Об одном классе мономиальноподобных абелевых кодов с кратными корнями.
Журнал комбинаторики алгебры, дискретных структур и приложений.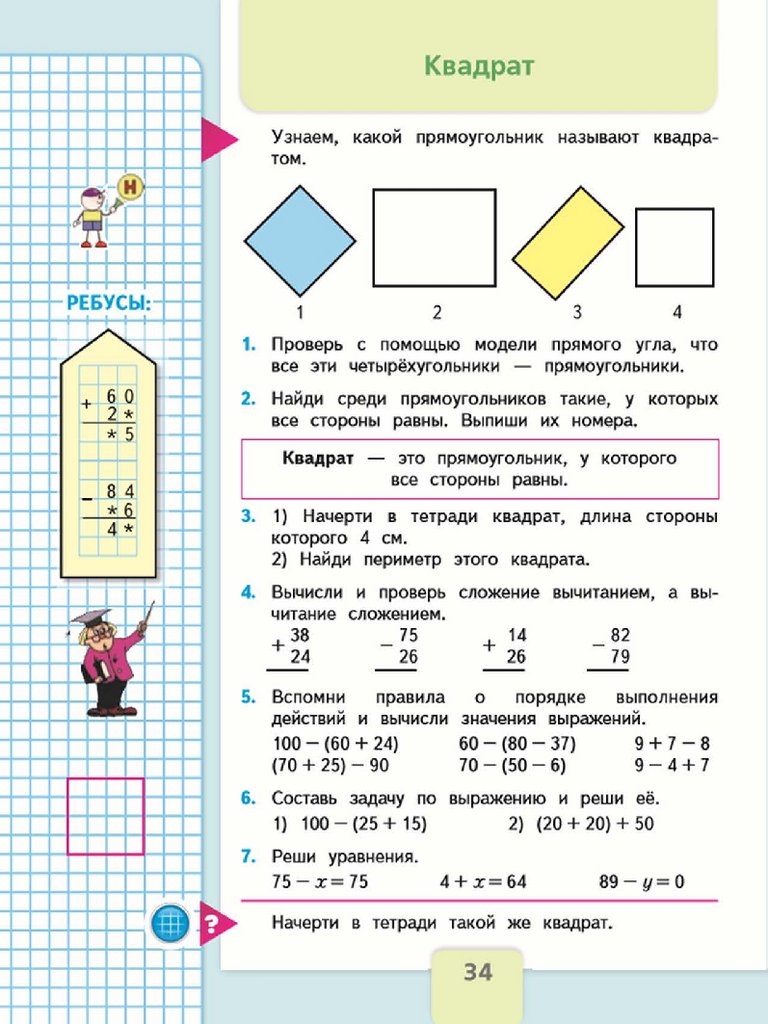 2015 г.;
2(2):
75-84. |
| IEEE | Э. Мартинес-моро
, Х. Озадам
, Ф. Озбудак
и С. Сабо
,
«Об одном классе мономиальноподобных абелевых кодов с кратными корнями», Журнал комбинаторики алгебры Дискретные структуры и приложения ,
об. 2,
нет. 2,
стр.
75–84, апрель 2015 г., doi:10.13069/jacodesmath.17537 |
Многостадийный непрерывный синтез выделяемых Nh3-сульфамидинов посредством нуклеофильного присоединения к переходному сульфурдиимиду
1.
1a. Das P., Delost M.D., Qureshi M.H., Smith D.T., Njardarson J.T., J. Med. хим. 2018, 62, 4265–4311; [PubMed] [Google Scholar]
1b. Девендар П., Ян Г.-Ф., Топ. Курс. хим. (З) 2017, 375, 10.1007/с41061-017-0169–9; [PubMed] [Google Scholar]
1c.
Lamberth C., J. Sulphur Chem.
2004, 25, 39–62. [Google Академия]
2. Скотт К. А., Ньярдарсон Дж. Т., Топ. Курс. хим. (З) 2018, 376, 10.1007/с41061-018-0184–5. [PubMed] [Google Scholar]
3.
3a. Mäder P., Kattner L., J. Med. хим. 2020, 63, 14243–14275; [PubMed] [Google Scholar]
3b. Sirvent J. A., Lücking U., ChemMedChem 2017, 12, 487–501; [Бесплатная статья PMC] [PubMed] [Google Scholar]
3c. Хан Ю., Син К., Чжан Дж., Тонг Т., Ши Ю., Цао Х., Ю Х., Чжан Ю., Лю Д., Чжао Л., Eur. Дж. Мед. хим. 2021, 209, 112885; [PubMed] [Google Scholar]
3d. Frings M., Bolm C., Blum A., Gnamm C., Eur. Дж. Мед. хим. 2017, 126, 225–245; [PubMed] [Google Scholar]
3e. Тилби М.Дж., Уиллис М.С., Мнение эксперта. Открытие наркотиков 2021, 16, 1227–1231. [PubMed] [Google Scholar]
4. Chinthakindi P.K., Naicker T., Thota N., Govender T., Kruger HG, Arvidsson P.I., Angew. хим. Междунар. Эд. 2017, 56, 4100–4109; [PubMed] [Академия Google] Ангью. хим. 2017, 129, 4160–4170. [Академия Google]
5.
Люкинг У., Орг. хим. Передний.
2019, 6, 1319–1324. [Google Scholar]
6. Некоторые примеры нашего вклада в эту область см.:
6a. Tota A., Zenzola M., Chawner S.J., John-Campbell S.S., Carlucci C., Romanazzi G., Degennaro L., Bull J.A., Luisi R., Chem. коммун. 2017, 53, 348–351; [PubMed] [Google Scholar]
6b. Zenzola M., Doran R., Degennaro L., Luisi R., Bull J.A., Angew. хим. Междунар. Эд. 2016, 55, 7203–7207; [Бесплатная статья PMC] [PubMed] [Google Scholar] Ангью. хим. 2016, 128, 7319–7323; [Google Scholar]
6c. Бриггс Э. Л., Тота А., Колелла М., Дегеннаро Л., Луизи Р., Булл Дж. А., Ангью. хим. Междунар. Эд. 2019, 58, 14303–14310; [PubMed] [Академия Google] Ангью. хим. 2019, 131, 14441–14448; [Google Scholar]
6д. Cividino P., Verrier C., Philouze C., Carret S., Poisson J., Adv. Синтез. Катал. 2019, 361, 1236–1240; [Google Scholar]
6e. Андресини М., Колелла М., Дедженнаро Л., Луизи Р., Аркивок 2021, 2021, 141–163. [Google Scholar]
7.
О синтезе сульфоксиминов см.:
7а. Bizet V., Hendriks C.M.M., Bolm C., Chem. соц. преп. 2015, 44, 3378–3390; [PubMed] [Google Scholar]
7b. Andresini M., Tota A., Degennaro L., Bull J.A., Luisi R., Chem. Евро. Дж. 2021, 27, 17293–17321. [Бесплатная статья PMC] [PubMed] [Google Scholar]
8. О синтезе сульфонимидамидов см.: Nandi G.C., Arvidsson P.I., Adv. Синтез. Катал. 2018, 360, 2976–3001. [Google Академия]
9. Davies T.Q., Willis M.C., Chem. Евро. Дж. 2021, 27, 8918–8927. [Бесплатная статья PMC] [PubMed] [Google Scholar]
10.
10а. Davies T.Q., Tilby M.J., Skolc D., Hall A., Willis M.C., Org. лат. 2020, 22, 9495–9499; [Бесплатная статья PMC] [PubMed] [Google Scholar]
10b. Davies T.Q., Tilby M.J., Ren J., Parker N.A., Skolc D., Hall A., Duarte F., Willis M.C., J. Am. хим. соц. 2020, 142, 15445–15453; [Бесплатная статья PMC] [PubMed] [Google Scholar]
10c. Zhang Z.-X., Davies T.Q., Willis M.C., J. Am. хим. соц. 2019, 141, 13022–13027; [Бесплатная статья PMC] [PubMed] [Google Scholar]
10д.
Ding M., Zhang Z.-X., Davies T.Q., Willis M.C., Org. лат.
2022, 24, 1711–1715; [Бесплатная статья PMC] [PubMed] [Google Scholar]
10e. Дэвис Т. К., Холл А., Уиллис М. К., Ангью. хим. Междунар. Эд. 2017, 56, 14937–14941; [PubMed] [Академия Google] Ангью. хим. 2017, 129, 15133–15137; [PubMed] [Google Scholar]
10f. Lo P.K.T., Willis M.C., J. Am. хим. соц. 2021, 143, 15576–15581; [PubMed] [Google Scholar]
10g. Бремерих М., Конрадс С.М., Ланглетц Т., Болм С., Angew. хим. Междунар. Эд. 2019, 58, 19014–19020; [Бесплатная статья PMC] [PubMed] [Google Scholar] Ангью. хим. 2019, 131, 19190–19196. [Google Scholar]
11.
11a. Ferry A., Billard T., Langlois B.R., Bacqué E., J. Org. хим. 2008, 73, 9362–9365; [PubMed] [Google Scholar]
11b. Natsugari H., Whittle R.R., Weinreb S.M., J. Am. хим. соц. 1984, 106, 7867–7872; [Google Scholar]
11c. Коваль И. В., рус. Дж. Орг. хим. 2002, 38, 232–234. [Академия Google]
12.
12а.
Андрезини М.
, Спеннаккио М., Романацци Г., Чириако Ф., Кларксон Г., Дедженнаро Л., Луизи Р., Org. лат.
2020, 22, 7129–7134; [PubMed] [Google Scholar]
12b. Андресини М., Спеннаккио М., Колелла М., Лосито Г., Арамини А., Дедженнаро Л., Луизи Р., Org. лат. 2021, 23, 6850–6854; [PubMed] [Google Scholar]
12c. Матос П. М., Стокман Р. А., Org. биомол. хим. 2020, 18, 6429–6442; [PubMed] [Google Scholar]
12d. Матос П. М., Льюис В., Мур Дж. К., Стокман Р. А., Org. лат. 2018, 20, 3674–3677. [PubMed] [Академия Google]
13. Чжан З.-Х., Уиллис М.С., хим. 2022, 8, 1137–1146. [Google Академия]
14. Zhang Z.-X., Bell C., Ding M., Willis M.C., J. Am. хим. соц. 2022, 144, 26, 11851–11858. [Бесплатная статья PMC] [PubMed] [Google Scholar]
15.
15a. Power M., Alcock E., McGlacken G.P., Org. Процесс Рез. Дев. 2020, 24, 1814–1838; [Google Scholar]
15б. Колелла М., Нагаки А., Луизи Р., Chem. Евро. Дж. 2019, 26, 19–32. [PubMed] [Google Scholar]
16.
16а. Хартман Р.Л., Curr. мнение хим. англ. 2020, 29, 42–50; [Google Scholar]
16б. Порта Р., Беналья М., Пульизи А., Org. Процесс Рез. Дев. 2015, 20, 2–25; [Google Scholar]
16c. Бауманн М., Муди Т.С., Смит М., Уорри С., Org. Процесс Рез. Дев. 2020, 24, 1802–1813. [Google Scholar]
17.
17a. Зибарев А. В., Лорк Э., Мьюс Р., Chem. коммун. 1998, 991–992; [Google Scholar]
17б. Багрянская И. Ю., Гатилов Ю. В., Шакиров М. М., Зибарев А. В., Менделеев коммун. 2002, 12, 167–168; [Академия Google]
17в. Лорк Э., Мьюз Р., Шакиров М.М., Уотсон П.Г., Зибарев А.В., J. Fluorine Chem. 2002, 115, 165–168. [Google Академия]
18. Шахбазян С., Захеди М., Нг С.В., Дж. Мол. Спектроск. 2004, 223, 195–204. [Google Академия]
19. Rouviere J., Tabacic V., Fleury G., Spectrochim. Акта А Мол. биомол. Спектроск. 1973, 29, 229–242. [Google Scholar]
20. Депонированные номера 2173063 ( 2 ae ) и 2173064 ( 2 am ) содержат дополнительные кристаллографические данные для этой статьи.