Спиши № 152 ГДЗ Математика 4 класс Моро М.И. – Рамблер/класс
Спиши № 152 ГДЗ Математика 4 класс Моро М.И. – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
Спиши, заполняя пропуски.
620 = □ дес. 756 = □ дес. □ ед. 1 000 см = □ м
□ ед. 1 000 см = □ м
620 дм = □ м 756 дм = □ м □ дм 6 000 мм = □ м
ответы
620 = 62 дес.
756 дм = 75 м 6 дм
1 000 см = 10 м
25 000 м = 25 км
6000 мм = 6 м
620 мм = 62 см
620 дм = 62 м
756 = 75 дес. 6 ед.
756 мм = 75 см 6 мм
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
3 класс
5 класс
Репетитор
Химия
похожие вопросы 5
Выполни деление № 60 ГДЗ Математика 4 класс Моро М.И.
Выполни деление с объяснением.
564:4 471 : 3 296 : 2 792 : 4 (Подробнее.
ГДЗМатематика4 классМоро М.И.
Привет! Кто знает ответы? Lesson 30. № 11. ГДЗ Английский язык 4 класс Верещагина.
Answer the following questions.
1. Where and when did the King and the Queen live? (Подробнее…)
ГДЗАнглийский язык4 классВерещагина И.Н.
ЕГЭ Математика 11 класс. Ященко И. В. Тренировочная работа 13 Вопрос 9 Найдите вероятность того, что Толя не выиграет.
Привет. Выручайте с ответом по математике…
Коля и Толя играют в кости. Они бросают кубик по одному разу, выигрывает тот, у кого (Подробнее…)
ЕГЭМатематикаЯщенко И.В.Семенов А.В.11 класс
ЕГЭ Математика 11 класс. Ященко И. В. Тренировочная работа 13 Вопрос 10 Найдите вероятность того, что будут дежурить мальчик и девочка.
Привет всем! Нужен ваш совет, как отвечать…
В классе 12 мальчиков и 13 девочек. 1 сентября случайным образом определяют двух (Подробнее.
ЕГЭМатематикаЯщенко И.В.Семенов А.В.11 класс
Как вы решили №32.4? Поделитесь гдз по алгебре 7 класс Мордкович?
Разложите многочлен на множители:
а) 7kn — 6k — 14n + 12; в) 9m2 — 9mn — 5m + 5n;
б) 7х + 7а — 6ах — 5а2; (Подробнее…)
ГДЗАлгебра7 классМордкович А.Г.
4 класс. Моро. Учебник №1. Ответы к стр. 37
Числа от 1 до 1000
Величины.
Единицы длиныОтветы к стр. 37
151. 1) Прочитай таблицу единиц длины.
Запиши и запомни её.
| 1 км = 1 000 м 1 дм = 10 см 1 м = 10 дм 1 см = 10 мм |
2) Используя эту таблицу, узнай, сколько миллиметров в 1 дм; сколько сантиметров в 1 м.
1 дм = 100 мм
3) Во сколько раз 1 м больше, чем 1 мм?
1 м = 1 000 мм. 1 м больше, чем 1 мм в 1 000 раз.
1 м больше, чем 1 мм в 1 000 раз.
152. Спиши, заполняя пропуски.
620 = 1 000 м 756 = 75 дес. 6 ед.
620 мм = 62 см 756 мм = 75 см 6 мм
620 дм = 62 м 756 дм = 75 м 6 дм
1 000 см = 10 м
25 000 м = 25 км
6 000 мм = 6 м
153. От двух остановок, расстояние между которыми 1 км, отошли два пешехода. Один из них прошёл 140 м, а другой — 160 м. Каким стало расстояние между пешеходами?
1) Дополни условие, чтобы чертёж к задаче был таким:
От двух остановок, расстояние между которыми 1 км, отошли навстречу друг другу два пешехода. Один из них прошёл 140 м, а другой — 160 м. Каким стало расстояние между пешеходами?
1) 160 + 140 = 300 (м) — прошли оба пешехода.
1 км = 1 000 м
2) 1 000 — 300 = 700 (м) — расстояние между пешеходами
2) Измени условие задачи, чтобы чертёж стал таким:
От двух остановок, расстояние между которыми 1 км, отошли два пешехода в противоположных направлениях друг к другу. Один из них прошёл 140 м, а другой — 160 м. Каким стало расстояние между пешеходами?
Один из них прошёл 140 м, а другой — 160 м. Каким стало расстояние между пешеходами?
1) 160 + 140 = 300 (м) — прошли оба пешехода.
1 км = 1 000 м
2) 1 000 + 300 = 1 300 (м) — расстояние между пешеходами
О т в е т: расстояние между пешеходами стало 1 300 м.
154.
200 — 80 : 2 + 6 = 166 905 — 359 • 2 = 187
(300 — 90) : 3 + 7 = 77 801 — 198 • 4 = 9
600 — 120 : (4 + 2) = 580 703 — 135 • 5 = 28
552 : 8 = 69
836 : 4 = 209
978 : 3 = 326
155. Найди правило, по которому составлен ряд чисел, и запиши ещё 3 числа: 24, 23, 21, 18, 17, 15, 12, 11, 9, 6.
24 — 1 = 23, 23 — 2 = 21, 21 — 3 = 18,
18 — 1 = 17, 17 — 2 = 15, 15 — 3 = 12,
12 — 1 = 11, 11 — 2 = 9, 9 — 3 = 6.
1 560 км = 1 км 560 м
ЗАДАНИЕ НА ПОЛЯХ:
Ребус
х 106
9
954
ГДЗ по математике. Учебник. 4 класс. Часть 1. Моро М. И., Бантова М. А., Бельтюкова М. А., Волкова С. И., Степанова С. В.
Учебник. 4 класс. Часть 1. Моро М. И., Бантова М. А., Бельтюкова М. А., Волкова С. И., Степанова С. В.
Математика. 4 класс
152 Весна 2019: Syllabus, HW
КАЛЬКУЛЯТОР : Для этого курса требуется графический калькулятор. Мы традиционно использовали TI-83 или 83+ и рекомендуем любой из них, но можно использовать любой калькулятор с эквивалентными возможностями, например популярный TI-85 или 86. Калькуляторы
ВНИМАНИЕ : Ваше расписание может отличаться. В Math 152 есть много разделов. Порядок, в котором рассматриваются темы, скорость их изучения, точное время экзаменов и домашние онлайн-задания WebAssign будут варьироваться от раздела к разделу. Например: В таблице, которую вы видите ниже, Экзамен 1 запланирован на 12-ю лекцию. Вместо этого лектор может решить сдать экзамен во время 11-й лекции. В таблице указано, что раздел 7.7 пройден на 11-й лекции. Лектор может принять решение начать 7.7 в конце 10-й лекции и закончить во время 11-й лекции. Таблица является лишь приблизительным вариантом расписания, которому будут следовать на самом деле.
Вместо этого лектор может решить сдать экзамен во время 11-й лекции. В таблице указано, что раздел 7.7 пройден на 11-й лекции. Лектор может принять решение начать 7.7 в конце 10-й лекции и закончить во время 11-й лекции. Таблица является лишь приблизительным вариантом расписания, которому будут следовать на самом деле.
Финальный экзамен отличается. Все разделы Math 152 будут сдавать заключительный экзамен в четверг, 9 мая 2019 г., с 16:00 до 19:00. Места проведения финальных экзаменов будут объявлены в апреле. Место проведения вашего окончательного экзамена может не совпадать с помещением, в котором проходят ваши лекции. Если у студента возникла чрезвычайная ситуация или иная веская причина для переноса выпускного экзамена, то этот студент должен связаться с преподавателем по поводу повторного экзамена на более поздний (не ранее) срок. Также будут отчеты о семинарах, которые должны быть сделаны на бумаге.
Точное время и охват экзаменов в течение семестра будут объявлены каждым преподавателем. Как студент в Math 152, ваши обязательства будут установлены и объявлены вашими отдельными преподавателями, и вы узнаете их, только посетив свой собственный класс. Лекции проходят два раза в неделю. Каждую неделю проходит мастер-класс. Мы НЕ отменяем семинары, первая встреча которых проводится до первой лекции.
Как студент в Math 152, ваши обязательства будут установлены и объявлены вашими отдельными преподавателями, и вы узнаете их, только посетив свой собственный класс. Лекции проходят два раза в неделю. Каждую неделю проходит мастер-класс. Мы НЕ отменяем семинары, первая встреча которых проводится до первой лекции.
Ваш лектор объявит схему оценивания по вашему разделу Math 152. Для определения вашей оценки по курсу будут использоваться ваши баллы за Экзамен 1, Экзамен 2, итоговый экзамен, отчеты о семинарах, домашние онлайн-задания WebAssign и тесты.
| Лекция | Разделы | Темы | Рекомендуемые упражнения из учебника |
|---|---|---|---|
| 1 | 5.7 и 6.1 | Метод замещения и площади между двумя кривыми | 5.7: 15, 19, 22, 23, 25, 27, 28, 31, 33, 35, 41, 42, 47, 50, 53, 54, 57, 58, 67, 68 6.1: 4, 9, 12 , 17, 18, 21, 23, 25 |
| 2 | 6,2 | Установка интегралов, объема, плотности, среднего значения | 6. 2: 4, 5, 6, 7, 9, 10, 11, 15, 25, 26, 40, 42, 44, 46, 48 2: 4, 5, 6, 7, 9, 10, 11, 15, 25, 26, 40, 42, 44, 46, 48 |
| 3 | 6,3 | Объемы оборота | 6.3: 7, 10, 12, 17, 19, 22, 30, 31, 32 |
| 4 | 6,4 | Метод цилиндрических оболочек | 6.4: 8, 10, 17, 20, 25, 29, 33, 37, 38 |
| 5 | 7.1 | Интеграция по частям | 7.1: 6, 10, 14, 22, 23, 26, 37, 50, 55, 56, 58, 60, 63, 76 |
| 6 | 7,2 | Тригонометрические интегралы | 7.2: 1, 2, 13, 16, 18, 20, 34, 37, 40, 49, 55, 62, 67, 71, 72, 75 |
| 7 | 7,3 | Тригонометрическая замена | 7.3: 5, 6, 9, 10, 15, 16, 17, 22, 26, 29, 34, 35, 40, 43 |
| 8 | 7,4 | Интегралы с гиперболическими и обратными гиперболическими функциями | 7.4: 11, 12, 24, 25, 31, 32, 35 |
| 9 | 7,5 | Метод неполных дробей | 7,5: 4, 8, 12, 14, 17, 20, 33, 34, 41 |
| 10 | 7,6 | Стратегии интеграции | 7. 6: 12, 13, 19, 20, 23, 28, 29, 32, 35, 38, 40, 43, 48, 54, 57 6: 12, 13, 19, 20, 23, 28, 29, 32, 35, 38, 40, 43, 48, 54, 57 |
| 11 | 7,7 | Несобственные интегралы | 7.7: 8, 11, 12, 16, 23, 29, 35, 36, 37, 41, 44, 53, 54, 57, 59, 67, 68, 71, 73 |
| 12 | Экзамен 1 | В классе, где читаются лекции | |
| 13 | 7,9 | Численное интегрирование | 7.9: 5, 10, 16, 18, 39, 40, 41, 42, 44, 47, 53 |
| 14 | 8.1 | Длина дуги и площадь поверхности | 8.1: 3, 4, 7, 9, 10, 17, 27, 29, 36, 38, 40, 42 |
| 15 | 10,1 | Последовательности | 10.1: 14, 18, 23, 26, 27, 30, 43, 44, 52, 53 |
| 16 | 10,2 | Суммирование бесконечного ряда | 10.2: 4, 6, 8, 11, 12, 14, 17, 20, 21, 24, 26, 27, 30, 31, 38, 40 |
| 17 | 10,3 | Сходимость ряда с положительными членами | 10. 3: 4, 5, 9, 10, 11, 17, 18, 20, 24, 25, 27, 37, 39, 42, 43, 52, 53, 55, 60, 62, 69 3: 4, 5, 9, 10, 11, 17, 18, 20, 24, 25, 27, 37, 39, 42, 43, 52, 53, 55, 60, 62, 69 |
| 18 | 10,4 | Абсолютная и условная сходимость | 10.4: 3, 8, 10, 13, 21, 22, 23, 24, 28 |
| 19 | 10,5 | Соотношение и корневой тест. Стратегии выбора тестов. | 10,5: 4, 7, 11, 14, 15, 22, 24, 25, 27, 38, 39, 47, 52, 59 |
| 20 | 10,6 | Силовая серия | 10.6: 9, 10, 14, 16, 19, 25, 26, 30, 31, 38, 39, 45 |
| 21 | 8,4 и 10,7 | Полиномы Тейлора и ряды Тейлора | 8.4: 4, 8, 15, 17, 21, 22, 31, 32, 37, 45, 46 10.7: 4, 12, 18, 20, 21, 30, 31, 32, 39, 41, 42, 48 , 53, 54 |
| 22 | Экзамен 2 | В классе, где читаются лекции | |
| 23 | 11.1 | Параметрические уравнения | 11.1: 8, 10, 12, 14, 18, 20, 21, 22 |
| 24 | 11,2 | Параметрическая длина дуги и скорость | 11.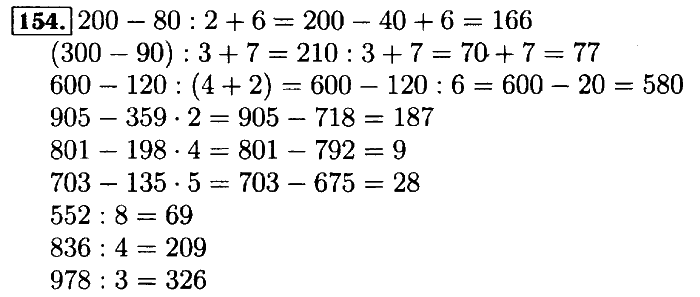 2: 6, 7, 8, 9, 11, 12, 21, 22 2: 6, 7, 8, 9, 11, 12, 21, 22 |
| 25 | 11,3 | Полярные координаты | 11.3: 3, 5, 6, 9, 12, 14, 16, 20, 27, 28 |
| 26 | 11,4 | Площадь и длина дуги в полярных координатах | 11.4: 7, 8, 9, 10, 13, 16, 25, 27, 30 |
| 27 | Конспект лекций по комплексным числам | Комплексные числа | |
| 28 | Конспект лекций по комплексным числам | Комплексные числа |
Успеваемость в США отстает от успеваемости многих других стран
Чем учащиеся США отличаются от своих сверстников по всему миру? Недавно опубликованные данные международных оценок по математике и естественным наукам показывают, что учащиеся США по-прежнему занимают среднее место в рейтинге и уступают многим другим развитым промышленным странам.
Одним из крупнейших межнациональных тестов является Программа международной оценки учащихся (PISA), которая каждые три года измеряет способность к чтению, математическую и естественную грамотность и другие ключевые навыки 15-летних в десятках развитых и развивающихся стран. . Согласно последним результатам PISA за 2015 год, США заняли невпечатляющее 38-е место из 71 страны по математике и 24-е место по естественным наукам. Среди 35 членов Организации экономического сотрудничества и развития, спонсирующей инициативу PISA, США заняли 30-е место по математике и 19-е место.й в науке.
. Согласно последним результатам PISA за 2015 год, США заняли невпечатляющее 38-е место из 71 страны по математике и 24-е место по естественным наукам. Среди 35 членов Организации экономического сотрудничества и развития, спонсирующей инициативу PISA, США заняли 30-е место по математике и 19-е место.й в науке.
Американские учащиеся младшего возраста несколько лучше справляются с аналогичной межнациональной оценкой, Trends in International Mathematics and Science Study. В этом исследовании, известном как TIMSS, тестировались учащиеся четвертого и восьмого классов каждые четыре года, начиная с 1995 года. В самых последних тестах, проведенных в 2015 году, 10 стран (из 48) имели статистически более высокие средние баллы по математике в четвертом классе, чем в США. , в то время как семь стран имели более высокие средние баллы по науке. В тестах для восьмого класса семь из 37 стран имели статистически более высокие средние баллы по математике, чем в США, а семь имели более высокие баллы по естественным наукам.
Другим длительным испытанием является Национальная оценка достижений в области образования, проект федерального департамента образования. В самых последних результатах NAEP за 2015 год средние баллы по математике для четвертых и восьмых классов упали впервые с 1990 года. Команда из Университета Рутгерса анализирует данные NAEP, чтобы попытаться определить причины снижения баллов по математике. .
Средний балл по математике четвертого класса NAEP в 2015 г. составил 240 (по шкале от 0 до 500), что соответствует уровню 2009 г.и по сравнению с 242 баллами в 2013 году. Средний балл восьмиклассников в 2015 году составил 282 балла по сравнению с 285 баллами в 2013 году; этот показатель был самым низким с 2007 года. (С 2005 года NAEP тестировала 12-классников по математике всего четыре раза; их средний балл 152 – по шкале от 0 до 300 в 2015 году был на один балл ниже, чем в 2013 и 2009 годах.)
С другой стороны, NAEP 2015 года оценил 40% четвероклассников, 33% восьмиклассников и 25% двенадцатиклассников как «продвинутых» или «продвинутых» в математике. Хотя сейчас намного меньше четверо- и восьмиклассников оценивают «ниже базового», самый низкий уровень успеваемости (18 % и 29% соответственно против 50 % и 48 % в 1990 г.), улучшение верхних уровней, похоже, застопорилось. (Среди 12-классников 38% набрали самый низкий уровень успеваемости по математике, что на балл ниже, чем в 2005 году.)
Хотя сейчас намного меньше четверо- и восьмиклассников оценивают «ниже базового», самый низкий уровень успеваемости (18 % и 29% соответственно против 50 % и 48 % в 1990 г.), улучшение верхних уровней, похоже, застопорилось. (Среди 12-классников 38% набрали самый низкий уровень успеваемости по математике, что на балл ниже, чем в 2005 году.)
NAEP также тестирует американских школьников по естественным наукам, хотя и не так регулярно, и имеющиеся ограниченные результаты указывают на некоторое улучшение. В период с 2009 по 2015 год средние баллы как четвероклассников, так и восьмиклассников улучшились со 150 до 154 (по шкале от 0 до 300), хотя для 12-классников средний балл остался на уровне 150. В 2015 г. 38% четвероклассники, 34% восьмиклассников и 22% двенадцатиклассников были оценены как продвинутые или лучше в естественных науках; 24% четвероклассников, 32% восьмиклассников и 40% 12-классников получили оценку «ниже базового».
Эти результаты вряд ли удивят многих. В отчете Pew Research Center за 2015 год только 29 % американцев оценили образование K-12 в своей стране в области естественных наук, технологий, инженерии и математики (известное как STEM) как выше среднего или как лучшее в мире.
