Краткая запись к задаче 4 класс математика: Математика 4 класс Моро

Стр. 60 — ГДЗ Математика 4 класс Учебник Моро Часть 1

1. Главная
2. ГДЗ
3. 4 класс
4. Математика
5. Моро учебник
6. Числа, которые больше 1000. Сложение и вычитание
7. Страница 60. Часть 1

Вернуться к содержанию учебника

Числа, которые больше 1000. Сложение и вычитание

Вопрос

260. (Устно.) Вычисли наиболее лёгким способом.

2 + 96 + 98 + 904	48 + 530 + 70 + 52
257 + 18 + 12 + 3 + 40	33 + 34 + 35 + 36 + 37

Ответ

Вопрос

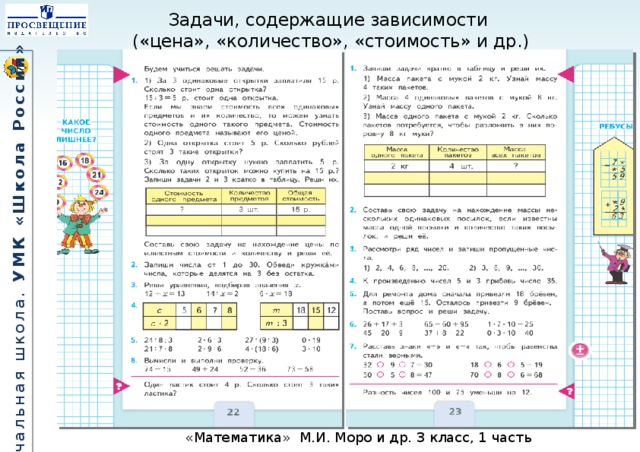
261. Объясни, что означают записи в рамках на полях.

Ответ

Вопрос

262. Вычисли, записывая решение столбиком, и проверь сложение вычитанием, а вычитание сложением.

528047 + 106875	320260 — 21476
385746 + 23352	605209 — 353672

Вопрос

263. В соревнованиях участвовало 18 семей, состоящих из 3 человек, и 16 семей, состоящих из 4 человек. Сколько это всего человек?

Ответ

Вопрос

264. После того как школьникам было выдано 327 книг, в библиотеке осталось на 246 книг меньше, чем было выдано. Сколько всего книг в библиотеке?

Ответ

Вопрос

265. Составь задачу по выражению 100 — (68 + 14).

Ответ

Вопрос

266. (Устно.)

999 + 1	10000 — 1	50000 — 1
1000 — 1	9999 + 1	80000 — 1

Ответ

Вопрос

1050 — 50

20000 + 800

35840 — 840

Ответ

Вопрос

Ребус

Ответ

Вернуться к содержанию учебника

---

ГДЗ по математике 4 класс учебник Моро, Бантова 1 часть

❤️️Ответ к странице 61.

Математика 4 класс учебник 1 часть. Авторы: М.И. Моро, М.А. Бантова.

Объясни вычисления.

Ответ:

Вычитаем единицы. От нуля отнять 6 мы не можем. Занимаем у десятков. В разряде десятков отсутствуют единицы. Занимаем у сотен. Одна сотня – это десять десятков. Теперь один десяток мы можем отдать. 10 – 6= 4. Записываем под единицами.
Вычитаем десятки. Мы добавили к десяткам одну сотню, то есть десять десятков, но при этом заняли десяток, осталось 9 дес. 9 – 2 = 7 Записываем под десятками.
Вычитаем сотни. Мы заняли одну сотню из шести, поэтому записываем пять сотен. Читаем ответ: 574.

Вычитаем единицы. Из нуля вычесть четыре нельзя, потому занимаем один десяток. Но единицы в разряде десятков отсутствуют, потому занимаем сотню. Единицы в разряде сотен отсутствуют, потому занимаем тысячу. Одина тысяча – это десять сотен, можем занять одну сотню.

Одна сотня – это десять десятков, теперь занимаем один десяток. Один десяток – это десять единиц. 10 – 4 = 6.
Вычисляем десятки. Мы добавили 10 десятков, но один заняли. 9 – 2 = 7 десятков. Вычисляем сотни. Мы добавили 10 сотен, но одну заняли, осталось 9. 9 – 1 = 8 сотен. Вычисляем единицы тысяч. Была 1 тысяча, но ее мы заняли. Осталось ноль, но его мы не пишем. Читаем ответ: 876.

Вычитаем единицы. Из семи вычесть восемь нельзя, потому занимаем один десяток. Но единицы в разряде десятков отсутствуют, потому занимаем сотню. Отсутствуют сотни и отсутствуют единицы тысяч, потому занимаем один десяток тысяч. Один десяток тысяч – это десять единиц тысяч, можем занять одну тысячу. Одна тысяча – это 10 сотен, можем занять из сотен. Одна сотня – это десять десятков, теперь занимаем один десяток. Один десяток – это десять единиц да ещё 7. 17 – 8 = 9.

Вычисляем десятки. Мы добавили 10 десятков, но один заняли. 9 – 4 = 5 десятков. Вычисляем сотни. Мы добавили 10 сотен, но одну заняли, осталось 9. 9 – 6 = 3 сотни. Вычисляем единицы тысяч. Мы добавили 10 единиц тысяч, но одну заняли, осталось 9 единиц тысяч. Переписываем 9, так как единицы тысяч в вычитаемом отсутствуют. Осталось два десятка тысяч, их переписываем. Читаем ответ: 29 359.

Номер 267.

Ответ:

Номер 268.

Проверь, верны ли равенства.

Ответ:

7 км 080 м = 7 • 1 000 + 80 = 7 080 м. 7 км 080 м ≠ 70 800 м, равенство неверно.

10 т 300 кг = 10 • 1000000 + 300 • 1000 = 10 300 000 г. 10 т 300 кг ≠ 10 300 г, равенство неверно.
3 м² = 3 • 10 000 = 30 000 см² 3 м² ≠ 20 000 см², равенство неверно.
4 ч = 4 • 60 = 240 мин 4 ч ≠ 100 мин, равенство неверно.
8 мин 20 с = 8 • 60 + 20 = 500 с 8 мин 20 с = 500 с, равенство верно.
20 км² = 20 • 1 000 000 = 20 000 000 м² 20 км² = 20 000 000 м², равенство верно.

Номер 269.

(Устно.) Заполни пропуски.

Ответ:

В 1 тыс. – 10 сотен, в 1 с. – 10 дес., в 1 дес. – 10 ед., в 1 мил. – 10 сот. тыс., в 1 с. тыс. – 10 дес. тыс., в 1 дес. тыс. – 10 тыс.

Номер 270.

В январе фабрика выпустила 4850 т бумаги, а в феврале − на 365 т меньше. Из всей этой бумаги 6335 т пошло на изготовление общих тетрадей, а из остальной бумаги сделали тонкие тетради. Поставь вопрос и реши задачу.

Ответ:

Вопрос: сколько тонн бумаги пошло на изготовление тонких тетрадей? Задачу можно оформить краткой записью или с помощью схемы.

Номер 271.

Садовод разбил фруктовый сад прямоугольной формы. Ширина сада 50 м, а длина в 2 раза больше ширины. Сколько деревьев можно посадить на этой площади, если отводить на одно дерево 10 м².

Ответ:

1) 50 ∙ 2 = 100 (м) – длина сада. 2) 50 ∙ 100 = 5000 (м²) – площадь сада. 3) 5000 : 10 = 500 (д.) – можно посадить в саду. Ответ: 500 деревьев.

Номер 272.

Найди частное и остаток. Выполни проверку.

Ответ:

Номер 273.

В 100 одинаковых вагонах можно перевезти 6000 т угля. В трёх таких вагонах помещается столько угля, сколько в двух большегрузных вагонах. Сколько тонн угля в одном большегрузном вагоне?

Ответ:

Эту задачу можно оформить с помощью краткой записи или таблицы: 100 вагонов – 6000 тонн угля. 3 вагона = 2 большегруза. 1 большегруз – ? тонн угля.

1) 6000 : 100 = 60 (т) – угля, в 1-ом вагоне. 2) 60 ∙ 3 = 180 (т) – угля, в 3-х вагонах. 3) 180 : 2 = 90 (т) Ответ: 90 тонн угля в большегрузном вагоне.

Номер 274.

Ответ:

Номер 275.

Какая доля каждой фигуры закрашена?

Ответ:

Первая фигура состоит из 12 клеток, а закрашено 6 клеток: 12 : 6 = 2, значит закрашена половина фигуры.
Вторая фигура состоит из 16 клеток, а закрашено 4 клетки: 16 : 4 = 4, значит закрашена четверть фигуры.

Задание внизу страницы

Ответ:

Рейтинг

Выберите другую страницу

1 часть

Учебник Моро	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63	64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79	80	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95	96	97	98	99	100	101	102	103	104	105	106	107	108	109	110	111

2 часть

4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63	64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79	80	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95	96	97	98	99	100	101	102	103	104	105	106	107	108	109	110	111	112	113	114	115	116	117	118	119	120	121	122	123	124	125	126	127

Что такое задача производительности? (Часть 1) | by Defined Learning

Задание на выступление – это любая учебная деятельность или оценка, которая требует от учащихся выполнения , чтобы продемонстрировать свои знания, понимание и мастерство. Задания на производительность дают ощутимый продукт и/или результаты, которые служат свидетельством обучения. В отличие от элемента с выбранным ответом (например, множественный выбор или сопоставление), в котором учащимся предлагается выбрать из заданных альтернатив, задание на производительность представляет собой ситуацию, которая требует от учащихся применить свои знания в контексте.

Задания на исполнение обычно используются в определенных дисциплинах, таких как изобразительное и исполнительское искусство, физическое воспитание и профессиональные технологии, где представление является естественным фокусом обучения. Однако такие задания можно (и нужно) использовать в каждой предметной области и во всех классах.

Характеристики исполнительских заданий

Хотя любое действие учащегося может считаться исполнительским заданием (например, завязывание шнурков или рисование картинки), полезно различать применение конкретных и дискретных навыков (например, ведение мяча в мяч). баскетбол) от реальной игры в контексте (например, игра в баскетбол, в которой дриблинг является одним из многих прикладных навыков). Таким образом, когда я использую термин задачи на исполнение, я имею в виду более сложные и аутентичные действия.

Вот семь основных характеристик заданий на выполнение:

1. Задания на выполнение требуют применения знаний и навыков, а не только припоминания или узнавания.

Другими словами, учащийся должен фактически использовать свои знания для выполнения . Эти задачи обычно дают материальный продукт (например, графическое изображение, сообщение в блоге) или исполнение (например, устную презентацию, дебаты), которые служат доказательством их понимания и мастерства.

2. Задания на производительность являются открытыми и обычно не дают единого правильного ответа.

В отличие от заданий с выборочным или кратким сконструированным ответом, которые ищут «правильный» ответ, рабочие задания не имеют конца. Таким образом, могут быть разные ответы на задачу, которые по-прежнему соответствуют критериям успеха. Эти задачи также открыты с точки зрения процесса; т. е. обычно не существует единственного способа выполнения задачи.

3. Задания на исполнение создают новые и аутентичные контексты для исполнения.

Эти задания представляют собой реалистичные условия и ограничения для учащихся. Например, задача по математике ставит перед учащимися невиданную ранее проблему, которую нельзя решить, просто «подставив» числа в заученный алгоритм. В подлинном задании учащиеся должны учитывать цели, аудиторию, препятствия и варианты для достижения успешного продукта или производительности. У аутентичных задач есть побочное преимущество — они сообщают учащимся цель и актуальность, помогая учащимся увидеть причину, по которой они прилагают усилия при подготовке к ним.

4. Задания на выполнение обеспечивают доказательство понимания посредством переноса.

Понимание проявляется, когда учащиеся могут перенести свое обучение на новые и «беспорядочные» ситуации. Обратите внимание, что не все выступления требуют переноса. Например, игра на музыкальном инструменте по нотам или пошаговое выполнение научной лаборатории требуют минимального переноса. Напротив, насыщенные задания на производительность являются открытыми и вызывают «мышление более высокого порядка» и вдумчивое применение знаний и навыков в контексте, а не выполнение по сценарию или по шаблону.

5. Задачи производительности многогранны.

В отличие от традиционных тестовых «элементов», которые обычно оценивают один навык или факт, рабочие задания более сложны. Они включают несколько этапов и, таким образом, могут использоваться для оценки нескольких стандартов или результатов.

6. Рабочие задания могут включать в себя два или более предметов, а также навыки 21-го века.

В более широком мире за пределами школы большинство вопросов и проблем не представляются четко в рамках «бункеров» предметной области. В то время как задания на эффективность, безусловно, могут быть специфичными для содержания (например, математика, естественные науки, социальные науки), они также обеспечивают средство для интеграции двух или более предметов и/или вплетения в навыки и привычки 21-го века. Одним из естественных способов интеграции предметов является включение компонента чтения, исследования и/или коммуникации (например, письмо, графика, устная или технологическая презентация) в задачи в таких областях содержания, как социальные науки, наука, здоровье, бизнес, здоровье/физическое воспитание. . Такие задания побуждают учащихся рассматривать значимое обучение как интегрированное, а не как нечто, происходящее в отдельных предметах и ​​сегментах.

7. Выполнение открытых заданий оценивается по установленным критериям и рубрикам.

Поскольку эти задания не дают единого ответа, продукты и успеваемость учащихся следует оценивать по соответствующим критериям, соответствующим оцениваемым целям. Четко определенные и согласованные критерии позволяют проводить обоснованную оценку на основе суждений. Более подробные оценочные рубрики, основанные на критериях, используются для профилирования различных уровней понимания и владения языком.

Давайте рассмотрим несколько примеров рабочих заданий, которые отражают эти характеристики:

Ботанический дизайн (старший базовый уровень)

Ваша ландшафтная архитектурная фирма борется за грант на реконструкцию общественного пространства в вашем районе и улучшение его внешний вид и полезность. Целью гранта является создание общественной зоны, где люди могут собраться, чтобы насладиться собой и местными растениями региона. Грант также направлен на информирование людей о типах деревьев, кустарников и цветов, произрастающих в этом регионе.
Ваша команда будет нести ответственность за выбор общественного места в вашем районе, которое вы можете улучшить для посетителей и членов сообщества. Вам нужно будет исследовать выбранную область, создать масштабный чертеж планировки территории, которую вы планируете реконструировать, предложить новый дизайн, включающий местные растения вашего региона, и подготовить учебные материалы, которые вы включите в дизайн.

Ознакомьтесь с полным заданием производительности из Defined STEM , здесь: Ботаническое задание производительности дизайна. Defined STEM — это онлайн-ресурс, где вы можете найти сотни заданий на выполнение проектов, соответствующих стандартам K-12.

Оценить заявку (старшая начальная/средняя школа)

Компания Pooper Scooper Kitty Litter Company утверждает, что их наполнитель на 40% более впитывающий, чем другие бренды. Вы являетесь исследователем защиты прав потребителей, которого попросили оценить их заявление. Разработать план проведения расследования. Ваш план должен быть достаточно конкретным, чтобы исследователи лаборатории могли следовать ему для оценки заявления.

Переезд в Южную Америку (средняя школа)

Поскольку они знают, что вы только что закончили модуль по Южной Америке, ваши тетя и дядя попросили вас помочь им решить, где им жить, когда ваша тетя начнет свою новую работу в качестве консультанта в компьютерной компании, работающей по всему региону. Они могут жить в любой точке континента.

Ваша задача состоит в том, чтобы исследовать возможные места для проживания, изучив соответствующие географические, климатические, политические, экономические, исторические и культурные факторы. Затем напишите письмо своим тете и дяде с рекомендацией места, куда им переехать. Обязательно объясните свое решение причинами и доказательствами из вашего исследования.

Расследование места происшествия (средняя школа)

Вы сотрудник правоохранительных органов, которого окружная прокуратура наняла для создания подразделения по расследованию места происшествия. Ваше первое задание состоит в том, чтобы вместе с репортером местной газеты разработать серию информационных материалов, чтобы проинформировать общественность о роли и преимуществах применения криминалистики при расследовании несчастных случаев.

Ваша команда будет делиться этой информацией с общественностью через различные медиа-ресурсы, принадлежащие газете и управляемые ею.

Ознакомьтесь с полным заданием на выполнение из Defined STEM здесь: Задание на исследование места происшествия

Таким образом, задания на выполнение, подобные этим, можно использовать для вовлечения учащихся в осмысленное обучение. Поскольку сложные задания на выполнение заданий создают аутентичный контекст, отражающий подлинное применение знаний, учащиеся часто мотивированы и вовлечены в такие задачи «реального мира».

При использовании в качестве оценивания задания на успеваемость позволяют учителям оценить понимание учащимися сложных процессов (например, исследование, решение задач и письмо), а не просто измерить отдельные знания. Они хорошо подходят для интеграции предметных областей и связывания знаний о содержании с навыками 21 века, такими как критическое мышление, творчество, сотрудничество, общение и использование технологий. Кроме того, оценка на основе результатов может также выявить привычки ума, такие как точность и настойчивость.

Воспользуйтесь бесплатной пробной версией Defined STEM, чтобы получить доступ к сотням реальных задач по повышению производительности. Для получения полного курса повышения квалификации по задачам производительности для вашей школы или округа см. Performance Task PD с Джеем МакТайем : http://www.performancetask.com

Для получения дополнительной информации о разработке и использовании производительности задачи см. Основное обучение: оценка того, что важнее всего -задача | Название статьи: Что такое задача производительности? | Название веб-сайта: PerformanceTask.com | Дата публикации: 12 апреля 2015 г.

Значение математики в повседневной жизни

Уважаемые родители,

Математика очень полезна в повседневной жизни. Математика может помочь нам сделать много вещей, которые важны в нашей повседневной жизни. Вот некоторые ежедневные задачи, для которых важна математика:

• Управление деньгами $$$
• Балансировка чековой книжки
• Покупки по лучшей цене
• Приготовление пищи
• Расчет расстояния, времени и стоимости поездки
• Понимание ссуд на автомобили, грузовики, дома, обучение или другие цели
• Понимание спорта (статистика игрока и команды)
• Воспроизведение музыки
• Выпечка
• Украшения для дома
• Шитье
• Садоводство и ландшафтный дизайн

Родители могут помочь подросткам связать математику, которую они изучают в школе, с повседневной жизнью. Как родитель, вы можете поговорить со своим подростком о том, как вы используете математику в своей повседневной жизни. Вы также можете спросить членов семьи и друзей, как они используют математику в своей повседневной жизни. Пожалуйста, поговорите со своими подростками об этих математических связях с реальным миром. Поделитесь с ребенком примерами повседневных математических приложений, которые перечислены ниже. Когда ваши подростки узнают, как можно использовать математику каждый день, они, скорее всего, сочтут математику важной и ценной. Они также могут больше интересоваться математикой. Помните, что вы как родитель можете сильно повлиять на то, как ваш ребенок думает о математике.

Отзывы, размещенные на этом веб-сайте, содержат краткие примеры того, как люди используют математику в своей повседневной жизни. Пожалуйста, посмотрите это. Вы можете поделиться информацией из этих видео со своим подростком.

Примеры связи математики с повседневной жизнью

Управление деньгами

На уроках алгебры ваш подросток получит навыки, которые помогут ему с деньгами. Одним из важных навыков, которые они усвоят, является расчет процентов и сложных процентов. Ваш подросток может использовать этот навык для управления своими деньгами сейчас и когда вырастет. Этот навык также поможет им выбрать лучший банковский счет. Это также поможет им решить, какую кредитную карту лучше иметь. Люди, которые берут кредиты, должны понимать проценты. Это также поможет им найти лучшие способы сберегать и инвестировать деньги.

 

 

Любительский спорт

Геометрия и тригонометрия могут помочь вашим подросткам, которые хотят улучшить свои спортивные навыки. Это может помочь им найти лучший способ ударить по мячу, забросить мяч в корзину или бегать по дорожке. Базовые знания математики также помогают отслеживать спортивные результаты.

 

 

 

Отделка и ремонт дома

Вычисление площади является важным навыком. Он пригодится вашему подростку при перепланировке будущих домов и квартир. Это поможет вашему подростку узнать, сколько краски ему нужно купить, чтобы перекрасить комнату. Это также важный навык для тех, кто хочет уложить новую плитку в ванной или на кухне. Знание того, как рассчитать периметр, может помочь вашему ребенку решить, сколько пиломатериалов купить для отделки пола или потолка.

 

 

 

Кулинария

При приготовлении пищи люди используют математические знания. Например, очень часто используется половина или двойная часть рецепта. В этом случае люди используют пропорции и соотношения, чтобы сделать правильные расчеты для каждого ингредиента. Если рецепт требует 2/3 стакана муки, повар должен рассчитать, сколько составляет половину или двойную часть 2/3 стакана. Затем повар должен представить количество, используя стандартные меры, используемые в выпечке, такие как ¼ стакана, 1/3 стакана, ½ стакана или 1 стакан.

No related posts.