Решение задачи за 3 класс по математике: занимательные текстовые задачки, примеры и другие задания с ответами и решением

Содержание

Урок 31. задачи в 3 действия — Математика — 3 класс

Математика, 3 класс

Урок № 31. Задачи в 3 действия

Перечень вопросов, рассматриваемых в теме:

— как решать текстовые задачи в 3 действия арифметическим способом?

— какие наиболее эффективные способы используются для решения задач?

Глоссарий по теме:

Задача – это текст, содержащий численные компоненты

Задача – это сформулированный словами вопрос, ответ на который может быть получен с помощью арифметических действий.

Условие – это часть задачи, в которой рассказывается о том, что неизвестно, содержит числовые данные.

Вопрос – это часть задачи, в которой сообщается о том, что нужно узнать.

Основная и дополнительная литература по теме урока:

1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 86.

Гребнева Ю. А. Тематические тестовые работы по математике для 3 класса М.: Ювента, 2015, с. 4-6.

Теоретический материал для самостоятельного изучения

Математика – самая древняя из наук, она была и остаётся необходимой людям. Слово «математика» греческого происхождения. Оно означает «наука», «размышление».

В Древнем Вавилоне математика зародилась задолго до нашей эры. Вавилонские памятники в виде глиняных плиток (всего около 500 000, причем из них примерно лишь 150 с текстами математических задач и 200 с числовыми таблицами) с клинописными надписями хранятся в различных музеях мира.

В этих текстах мы находим достаточно удобные способы решения ряда практических задач, связанных с земледелием, строительством и торговлей.

В Древнем Египте, «стране пирамид» за много тысяч лет до нашей эры возводились гигантские сооружения в виде храмов и пирамид. Некоторые из этих памятников сохранились до настоящего времени. Различные строительные работы, а также земледелие, основанное на искусственном орошении, рано вызвали потребность в математических познаниях и особенно в геометрии.

Математические правила, нужные для земледелия, астрономии и строительных работ, древние египтяне записывали на стенах храмов или на «папирусах», лентообразных свитках из особого писчего материала растительного происхождения.

В Британском музее хранится так называемый «папирус Райнда». Рукопись относится к периоду 2000—1700 лет до нашей эры. В ней содержится 84 задачи, причем большинство из них арифметического характера.

Решение задач является неотъемлемой частью жизни человека. Начиная с древних времен и до наших дней, люди используют разные виды и способы решения задач. У одной задачи бывает только один способ решения, а у другой — их несколько.

Рассмотрим решение задачи.

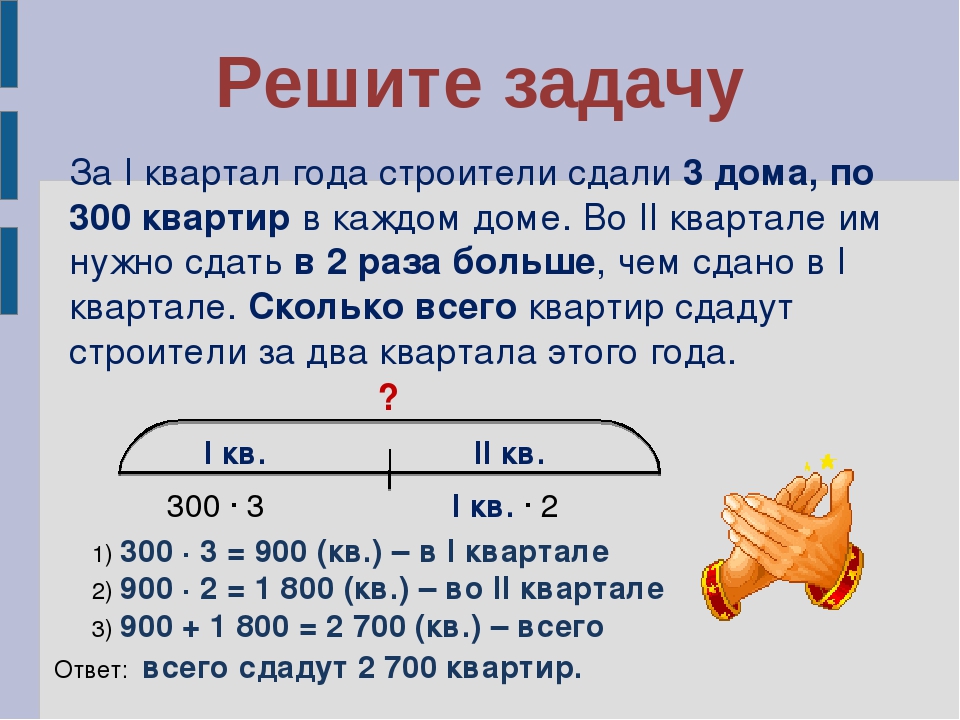
В детский сад привезли 4 коробки конфет по 9 кг в каждой, и 3 коробки печенья по 8 кг в каждой коробке. Сколько всего кг конфет и печенья привезли в детский сад?

Составим текстовую краткую запись задачи.

Конфеты — 4 кор. по 9 кг

Печенье — 3 кор. по 8 кг

? кг

Составим план решения этой задачи:

Первым действием надо узнать, сколько кг конфет привезли в детский сад (выполнить умножение).

Вторым действием узнаем, сколько кг печенья привезли в детский сад

(выполнить умножение).

Третьим действием узнаем, сколько конфет и печенья привезли в детский сад (выполнить сложение).

Запишем решение:

1) 9 ∙ 4 = 36 кг – конфеты

2) 8 ∙ 3 = 24 кг – печенье

3) 36 + 24 = 60 кг – всего

Ответ: 60 кг печенья и конфет привезли в детский сад.

Можно эту запись сократить и записать одним действием.

9 ∙ 4 + 8 ∙ 3 = 60 кг

Задания тренировочного модуля:

1. К каждому вопросу задачи подберите соответствующее выражение.

У продавца были воздушные шарики 3 цветов по 6 штук каждого цвета. Он продал по 4 шарика 2 цветов. Сколько шариков у него осталось?

Сколько шариков было?	6 ∙ 3 — 4 ∙ 2
Сколько продал шариков?	6 ∙ 3
Сколько шариков осталось?	4 ∙ 2

Правильный ответ:

Сколько шариков было?	6 ∙ 3
Сколько продал шариков?	4 ∙ 2
Сколько шариков осталось?	6 ∙ 3 — 4 ∙ 2

2. Выделите цветом верное решение задачи.

У Вали 5 конвертов с открытками по 7 открыток в каждом конверте. Она подарила 3 конверта по 4 открытки в каждом конверте. Сколько открыток у Вали осталось?

7 ∙ 5 + 4 ∙ 3;

7 ∙ 5 — 4 ∙ 3.

Правильный ответ:

7 ∙ 5 — 4 ∙ 3

213 задач и примеров по математике для 3 класса

Начальная школа, 1-4 классы

О.В. Узорова, Е.А. Нефедова Тренинговая тетрадь содержит 49 задач трёх уровней сложности. В конце

Начальная школа, 1-4 классы

О. И. Крупенчук Эта книга поможет вашим детям научиться читать быстро тексты любой сложности. В

Начальная школа, 1-4 классы

М. В. Беденко Учебное пособие содержит более 500 задач по программе 1 класса. Эти

Начальная школа, 1-4 классы

В. Н. Рудницкая Данное пособие содержит тематические тестовые задания, которые позволят оценить успешность освоения программы

Начальная школа, 1-4 классы

А.В. Ефимова, М.Р. Гринштейн В данной рабочей тетради представлены упражнения для повторения и закрепления

Начальная школа, 1-4 классы

О. Д. Ушакова Эта книга предназначена для того, чтобы вы могли проверить и закрепить знания,

Викторина по математике для 3 класса.

Автор:
Ковалева Наталья Михайловна,
учитель начальных классов
МОУ «СОШ № 61»

Цели:

Развитие логического, образного и творческого мышлении у обучающихся.

Задачи:

1. Вызвать интерес к предлагаемым вопросам, таким образом расширить кругозор учащихся
2. Формировать и развивать у учащихся умения и навыки работы в группе
3. Развивать мышление и творческую инициативу ребят

Форма работы: групповая.

Регламент: 30 минут или по окончанию решения всех задач, какой-либо группой.

Условия викторины:

За каждой командой закреплён судья. Командам предлагается одинаковый набор из 21 задач разных типов. Задачи представлены в виде экзаменационных билетов, выбор той или иной задачи зависит от выбора командира.

Командир берёт задачу у судьи, возвращается к группе, сообща решается задача, командир возвращается к судье с решением. Присуждение баллов: за каждую решенную верно задачу, группа получает 1 балл, на нерешенную задачу — 0 баллов, за отказ от решения — (-1) балл. Викторина заканчивается по истечению регламента или по окончанию решения всех задач, какой-либо группой. Нарушение условий викторины штрафуется — 1 баллом.

Победителем становится та команда, которая наберёт наибольшее количество баллов. ХОД ВИКТОРИНЫ

Этапы	Содержание урока	Время	Дополнения
I	Организационный момент. 1. Деление на группы в форме жеребьёвки (цветные фигурки). 2. Ознакомление с условиями викторины. 3. Работа в группе (придумывание название группы; выбор командира)	4 мин	1. Разлиновать доску; 2. Подготовить жетоны для жеребьёвки; 3. Распечатать условия викторины.
II	Решение задач.	30 мин	1. Подготовить тексты задачи для команд на листах разного цвета. 2. Подготовить листы-контролеры для судей. 3. Подготовить для судей «ключи» к задачам
III	Рефлексия: — Что особенно понравилось? — В чём возникли трудности? Почему? Что надо знать и уметь, чтобы не попадать в затруднения? — Что можете сказать своим партнёрам по групповой работе? — Что можете сказать своим соперникам? — Что можете пожелать всем участникам викторины?	5 мин	_
IV	Д/З. Подумайте над решением задач, при решении которых возникли затруднения. Мы эти задачки разберём на логике.	1мин	_

ЗАДАНИЯ ДЛЯ ГРУПП

Задача 1.
Сколько домов находится между домами № 26 и № 56, расположенными на одной стороне улицы?

Задача 2.
Сколько всего чётных чисел от 4 до 16, включая и названные числа?

Задача 3.
Сколько получиться, если из числа, выраженного тремя единицами второго разряда, вычесть число, выраженное пятью единицами первого разряда?

Задача 4.
Сколько квадратов изображено на рисунке?

Задача 5.
На прямой отметили 4 точки. Сколько всего получилось отрезков, концами которых являются эти точки?

A B C D
____________________________________________

Задача 6.
Вставьте пропущенные цифры в пример на сложение:
   * 6 *
   * 7
____________
      * * 2 4

Задача 7.
Вставьте пропущенное число, найдя закономерность числового ряда.
3 5 7 9
9 25 49 ?

Задача 8.
Чтобы разгадать ребус, нужно каждую букву заменить цифрой. Одинаковым буквам соответствуют одинаковые цифры. Разгадайте ребус.
F F + K = K R R

Задача 9.
Решите задачу.
Три котёнка — Касьянка, Том и Плут -съели плотвичку, окуня и карася. Касьянка не ел ни плотвичку, ни окуня. Том не ел плотвичку. Какую рыбу съел каждый котёнок?

Задача 10.
Решите задачу.
В школе 400 учеников. Верно ли утверждение, что хотя бы два ученика этой школы отмечают свой день рождения в один и тот же день года?

Задача 11.
Решите задачу.
У моего отца только один сын. А всего детей в семье трое. Как такое может быть, ведь у меня нет братьев?

Задача 12.
Решите задачу.
Гном разложил свои сокровища в три сундука разного цвета, стоящих у стены: в один — драгоценные камни, в другой — золотые монеты, в третий — магические книги. Он помнит, что красный сундук находится правее, чем сундук с камнями, и что сундук с книгами — правее красного сундука. В каком сундуке лежат книги, если зелёный сундук стоит левее синего, а зелёный и синий сундуки — крайние.

Задача 13.
Расставьте в клетках квадрата числа 1, 4, 6,7,8,9 так, чтобы во всех вертикальных и горизонтальных рядах, а также по диагоналям в сумме получилось 15.

___	___	___
___	_5_	_3_
_2_	___	___

Задача 14.
Решите задачу.
Машина за 40 минут проехала 40 км, а катер за 30 минут прошёл 35 км. Чья скорость больше?

Задача 15.
Решите задачу.
Белая мышка бежала от сарая к дому, а серая — от дома к сараю. Выбежали они одновременно. Через пять минут белая мышка была ближе к дому, чем серая к сараю. Какая мышка бежала медленнее?

Задача 16.
Решите задачу.
Как увеличить площадь бассейна вдвое, сохранив деревья и не изменив квадратную форму бассейна?

Задача 17.
Мы часто используем слово «километр». «Метр» в переводе с французского языка означает «мера», а что означает слово «кило»?
Выбери правильный вариант: мясо; тысяча; длина.

Задача 18.
Сколько получится, если из наименьшего четырёхзначного числа вычесть наибольшее однозначное?

Задача 19.
Решите задачу.
В магазин привезли 4 одинаковые полные коробки: в одной — апельсины, в другой — яблоки, в третий — мандарины, а в четвёртой — вишни. В какой коробке наибольшее число плодов?

Задача 20.
Решите задачу.
У семи братьев по одной сестре. Сколько детей в семье?

Задача 21.
Решите задачу.
На руках 10 пальцев. Сколько пальцев на 10 руках?

КЛЮЧИ К ЗАДАЧАМ

Тема 1. Нумерация.
Задача 1. (56 — 26) : 2 — 1= 14 домов
Задача 2. 7 чисел (4, 6, 8, 10, 12, 14, 16)
Задача 3. 30 — 5 = 25

Тема 2. Геометрические задачи.
Задача 4. 14 квадратов (9 маленьких, 4 средних, 1 большой)
Задача 5. 6 отрезков (AB, AC, AD, BC, BD, CD)

Тема 3. Арифметические действия, числовые и буквенные ребусы.
Задача 6.
   9 6 7
   5 7
____________
      1 0 2 4

Задача 7. Пропущено число 81 (9х9)
Задача 8. 99 + 1 = 100 (F = 9; K = 1; R = 0)

Тема 4. Логические задачи.
Задача 9. Ответ: Касьянка съел карася, Том — окуня, Плут — плотвичку.
Задача 10. Ответ: Да, т.к. в году 366 дней, соответственно минимум 34 пары учеников родились в один день.
Задача 11. Ответ: в семье — один сын и две дочери.
Задача 12. Ответ: книги лежат в синем сундуке. Решение: По условию сундук с камнями стоит левее красного, а сундук с книгами — правее красного. Значит, красный сундук стоит по середине, и в нём лежат золотые монеты. Так как зелёный и синий сундуки — крайние, и зелёный стоит левее синего, то зелёный — крайний слева, а синий — крайний справа. Вспомнив, что сундук с камнями находится левее, а сундук с книгами — правее красного сундука, приходим к выводу, что камни лежат в зелёном, а книги — в синем сундуке.

Тема 5. Магические квадраты.
Задача 13.

_6_	_1_	_8_
_7_	_5_	_3_
_2_	_9_	_4_

Тема 6. Задачи на движение.
Задача 14. Ответ: скорость катера была больше.
Задача 15. Ответ: медленнее бежала серая мышка.

Тема 7. Площадь фигур.
Задача 16. Изменить площадь бассейна вдвое, не изменив квадратную форму, можно так, как показано на схеме.

Тема 8. Величины.
Задача 17. Слово «кило» означает «тысяча»

Тема 9. Задачи на смекалку.
Задача 18. 1000 — 9 = 991
Задача 19. Ответ: плодов больше в коробке с вишнями.
Задача 20. Ответ: в семье 8 детей (7 сыновей и одна дочь)
Задача 21. Ответ: на десяти руках 50 пальцев.

Кемерово, 2010

Логические задачи по математике – 3 класс: решения и ответы

Логические задачи по математике для 3 класса

Логические задачи по математике для учеников 3 класса помогают детям развивать логическое мышление и улучшают сообразительность. Решение таких заданий хорошо тренирует мозг ребенка и закладывает в нем фундамент к дальнейшему развитию. Самое главное – заинтересовать юного математика. А сделать это можно только в том случае, если задания будут ему интересны. Предлагаем вашему вниманию примеры заданий на логическое мышление по математике для учащихся третьих классов.

Интересно! Интересные кроссворды для детей 7-8

Виды заданий

Существует несколько типов логических задач для учеников третьих классов:

•текстовые задачи в несколько действий;

•математические ребусы;

•задания на определение истины;

•классические задачи на логику.

Начнем наш обзор по порядку – с первого пункта.

Логические текстовые задачи в 2-3 действия

Решение заданий подобного рода очень хорошо развивает не только логическое мышление, но и формирует математический склад ума.

Пример №1 – задача на возрастающую закономерность

Условие. Серёжа построил четыре башни. Первая вышка состояла из 3 кубиков, а каждая последующая была выше на 2 кубика, чем предыдущая. Сколько для строительства всех четырех башен было использовано кубиков?

Решение и ответ. 3+5+7+9= 24. При строительстве четырех башен было использовано в общей сложности 24 кубика.

Пример №2 – задача на закономерность и рост

Условие. Саше подарили маленького щенка. Мальчик тут же замерил его рост. Оказалось, что он составляет 20 см. Спустя год Саша вновь замерил рост своего питомца, теперь он равнялся 36 см. Через год собака доросла до 44 см, а еще спустя год цифра на ростомере равнялась 48 см. Какого роста будет любимый пёс Саши еще через год, если имеющаяся закономерность роста сохранится?

Решение и ответ. Для начала необходимо проследить закономерность, по которой щенок прибавлял в росте. 36-20=16; 44-36=8; 48-44=4. Как мы видим, ежегодно прирост щенка уменьшается в 2 раза в сравнении с предыдущим. Следовательно, к следующему году питомец мальчика прибавит в росте 2 см, и эта цифра будет равняться 50см (48+2=50).

В школьной программе для 3 класс часто встречаются задачи на умножение и деление. Приведем несколько примеров по данной теме.

Пример №3 – задача на определение возраста

Условие. В одной семье проживает 4 детей разных возрастов. Их зовут Коля, Ваня, Оля и Аня. Известно, что им 4, 9,12 и 17 лет. Но кто из них какого возраста – непонятно. Подсказки:

•один из мальчиков посещает детский сад;

•Коля младше Ани;

•сумма дет Вани и Оли без остатка делится на 4.

Определите, сколько лет каждому из детей.

Решение и ответ. Используя метод деления, мы можем определить, что общий возраст Вани и Оли равняется 16 годам, так как именно это число без остатка делится на 4. Значит, кому-то из них 4, а кому-то – 12. Известно, что один мальчиков ходит в детский сад, значит, именно Ване 4 годика, а Оле – 12. Также известно, что Коля младше Ани, а это значит, что девочка самая старшая из детей в этой семье. Следовательно, Ане 17 лет, а Коле – 9.

Такие сложные логические задачи вполне могут встречаться и на олимпиадах по математике.

Пример №4 – задача на деление, сложение и вычитание

Условие. В магазине спортивных товаров продаются наборы из нескольких предметов.

Первый набор включает в себя: 10 мячей, 2 обруча и 10 скакалок. Его цена – 120 условных единиц.

Второй комплект включает: 7 мячей, 1 обруч и 6 скакалок. Его стоимость – 77 условных единиц.

Определите цену третьего комплекта, если он включает в себя: 2 мяча и 1 скакалку.

Решение и ответ. Для начала необходимо определить разницу в стоимости между первым и вторым набором (120-77=43). Получается, что 43 условных единицы – это стоимость 3 мячей, 1 обруча и 4 скакалок.

Интересно! Логические задачи по математике для 1 класса

Теперь отнимем эту цифру от стоимости 2 набора (77-43=34). Так мы узнаем цену 4 мячей и 2 скакалок. Следовательно, стоимость 2 мячей и 1 скакалки будет составлять 17 условных единиц (34÷2=17).

Математические ребусы

Среди логических задач по математике для 3 класса иногда встречаются ребусы. Задачи такого типа помогают ребенку развивать умение рассуждать и мыслить последовательно. Приведем пример.

Задача – математический ребус-таблица с фруктами

Условие. Рассмотрите предложенную таблицу. В ней указана общая цена фруктов по горизонтали и вертикали. Известно, что одинаковые фрукты имеют одинаковую цену. Определите стоимость персика.

Решение и ответ. Для начала необходимо внимательно рассмотреть таблицу на наличие одинаковых фруктов в столбцах и строках. Мы видим, что во второй строке находится 3 яблока общей стоимостью в 9 условных единиц. Узнаем цену 1 яблока (9÷3=3). Теперь обращаем внимание на второй столбец. Мы можем найти стоимость клубники (11-3х2=5). Теперь мы можем определить цену граната в нижней строке (18-3х5=3). Наконец, настало время выяснить, сколько стоит персик. Для этого решаем следующее выражение 26-(3+3+5)=15. Получается, что стоимость персика равняется 15 условным единицам.

Задачи на определение истины

Умение мыслить и логически рассуждать – именно эти качества тренируют задачи на определение истины. Предлагаем вашему вниманию два примера подобного типа заданий. Одно простое, а второе – олимпиадного уровня.

Пример №1 – простая задача

Условие. Фокусник, выступающий в цирке, вынес из-за кулис 3 коробки с надписями (смотрите фотографию). Он заявил, что совсем скоро собравшиеся зрители увидят собачек, голубей и кроликов. Определите, из какого ящичка фокусник достанет кроликов, если нам известно, что каждая из надписей на коробках – неправда.

Решение и ответ. Мы знаем, что фокусник пытается нас запутать, поэтому надпись «В первой коробке кролики» означает, что их там точно нет. Возле второй коробки находится надпись «Кролики». Это значит, что кролики точно не во втором ящике. У нас остается только один вариант. Получается, что кролики прячутся в коробке № 3.

Пример № 2 – задача для 3 класса повышенной сложности

Условие. Бабушка, дедушка и их внучка живут в одном подъезде трехэтажного дома, но на разных этажах. Известно, что бабушка проживает выше дедушки, внучка не на третьем этаже, а дедушка на 1 на не на 3 этаже. Кто на каком этаже живет, если известно, что одно из утверждений – ложь.

Решение и ответ. Утверждение, связанное с дедушкой является неправдивым. Дедушка живет на первом этаже, внучка на втором этаже, а бабушка – на третьем.

Классические задачи на логику

Школьная программа построена таким образом, что в 3 классе дети уже могут работать с числами: вычитать, складывать, делить и умножать их. Предлагаем вашему вниманию несколько интересных логических задач по математике.

Пример №1

Условие. Планируя свой очередной эксперимент, профессор приобрел 9 стержней из металла. Некоторые из них в ходе работ он распилил на 5 частей. В итоге у него стало 33 стержня. Определите, сколько стержней профессор распилил, и какое количество стержней остались нетронутыми.

Интересно! Объемные цветы из бумаги делаем пошагово

Решение и ответ. Следует понимать, что при распиле стержня на пять частей, количественно прибавляется 4 куска. В общей сложности добавилось 24 кусочка (33-9=24). Теперь мы можем определить, что профессор распилил 6 стержней (24÷4=6).

Пример №2

Условие. Мальчик играл в компьютерную игру, в которой ему нужно быть победить монстрика с помощью пистолета. Изначально у игрока было в запасе 9 выстрелов. Но по правилам игры, за каждое попадание в цель, мальчик получал еще 3 дополнительных выстрела. Определите, сколько раз парень попал в монстрика, если известно, что в общей сложности он выстрелил 30 раз и израсходовал при этом все выстрелы.

Решение и ответ. 30-9=21. Именно столько выстрелов мальчик получил дополнительно за попадания по монстрику. Известно, что за каждое попадание прибавлялось еще 3 попытки, значит, теперь мы можем найти общее количество попаданий 21÷3=7.

Надеемся, что логические задачи по математике для 3 класса с ответами и решениями, приведенные в статье, помогут вашему ребенку лучше разобраться в данном предмете и получать только лучшие оценки в школе.

ВПР по математике 3 класс 2020 Крылова Вариант 1

Всероссийская проверочная работа по математике за 3 класс, О.

Н. Крылова, 2020 года, вариант 1

Для написании данной работы были использованы задания из учебного пособия “Всероссийская проверочная работа: математика. 3 класс. Типовые тестовые задания. ФГОС. О.Н. Крылова. 2020 год.”

Часть 1

Задание 1

Запиши число, в котором 8 сотен 3 десятка и 1 единица.

Решение

8 сотен = 800

3 десятка = 30

1 единица = 1

800 + 30 + 1 = 831

Ответ:

831

Задание 2

На сколько число 648 больше числа 31.

Решение

Найдем разницу чисел 648 и 31

648 – 31 = 617

Ответ:

на 617

Задание 3

Запиши выражение.

Число 394 увеличить на частное чисел 720 и 9.

Решение

Частно чисел 720 и 9 ни что иное, как результат деления числа 720 на 9:

720 : 9

В задании сказано, что число 394 нужно увеличить “НА”, т.е. необходимо выполнить действие “сложение”, получим:

394 + 720 : 9

Скобки можно не использовать, поскольку “деление” будет выполняться в первую очередь.

Ответ:

394 + 720 : 9

Задание 4

Сравни значения выражений.

8 * 2 () 64 : 8

Решение

Найдем значение первого выражения:

8 * 2 = 16

Найдем значение второго выражения:

64 : 8 = 8

Получаем:

16 > 8

8 * 2 > 64 : 8

Ответ:

8 * 2 > 64 : 8

Задание 5

Длина прямоугольника 8 см. Она в 4 раза больше ширины.

Начерти этот прямоугольник.
Найди периметр прямоугольника.

Решение

Начерти этот прямоугольник.

Чтобы начертить заданный прямоугольник, найдем значение его ширины:

8 : 4 = 2 (см) – ширина прямоугольника

Найди периметр прямоугольника.

Известно, что ширина прямоугольника 2 см, а длина 8 см. Периметр будет равен:

P = 2 * (a + b) = 2 * (2 + 8) = 2 * 10 = 20

Ответ:

20 см

Задание 6

Где вычитание выполнено верно? Укажи номер примера.

Решение

Из представленных выражений, второе правильное

Ответ:

Задание 7

Укажи номер рисунка, в котором раскрашено 2/6 полоски

Решение

Нам необходимо найти полоску, в которой раскрашено 2 клетки из 6.

Это полоска №4

Ответ:

Задание 8

Найди значение выражения.

3 * (12 – 20 : 4)

Решение

Первое действие – выполним деление в скобках:

20 : 4 = 5

Второе действие – выполним вычитание в скобках:

12 – 5 = 7

Третье действие – найдем произведение:

3 * 7 = 21

Ответ:

Задание 9

В таблице приведены цены на одинаковые товары в трёх разных магазинах. В каком магазине банка кофе и пачка чая обойдутся дешевле всего?

Товар/Магазин	“Минутка”	“Для вас”	“Удобный”
Банка кофе	540 р.	500 р.	525 р.
Пачка чая	110 р.	120 р.	100 р.
Коробка конфет	190 р.	180 р.	185 р.

Решение

Стоимость банки кофе и пачки чая в магазине “Минутка”:

540 + 110 = 650 (р.)

Стоимость банки кофе и пачки чая в магазине “Для вас”:

500 + 120 = 620 (р.)

Стоимость банки кофе и пачки чая в магазине “Удобный”:

525 + 100 = 625 (р.)

Дешевле всего покупка обойдется в магазине “Для вас”

Ответ:

в магазине “Для вас”

Задание 10

Реши задачу. Запиши ответ.

За 2 детских стульчика заплатили 360 р. Сколько можно купить таких стульчиков за 900 р.?

Решение

Найдём стоимость 1 стульчика:

360 : 2 = 180 (р.)

Определим, сколько стульчиков можно купить на 900 р.:

900 : 180 = 5 (с.)

Ответ:

5 стульчиков.

Часть 2

Задание 11

Реши задачу.

В одном альбоме 360 монет, что на 100 монет больше, чем в другом альбоме. Сколько всего монет в двух альбомах?

Решение

Найдем количество монет во втором альбоме:

360 – 100 = 260 (м.)

Определим общее количество монет в обоих альбомах:

360 + 260 = 620 (м.)

Ответ:

620 монет

Задание 12

Реши задачу.

В 3 “А” классе учатся спортсмены. Среди них плаванием занимается 19 человек, гимнастикой – 17 человек, а плаванием и гимнастикой – 12 человек. Сколько всего человек в классе

Решение

Способ 1

19 – 12 = 7 (ч.) – занимается только плаванием

7 + 17 = 24 (ч.) – всего человек в классе

Способ 2

17 – 12 = 5 (ч.) – занимается только гимнастикой

5 + 19 = 24 (ч.) – всего человек в классе

Способ 3

19 + 17 = 36 (ч.) – занимается плаванием и/или гимнастикой

36 – 12 = 24 (ч.) – всего человек в классе

Ответ:

24 человека

«Полный сборник задач по математике.

3 класс. Все типы задач. Контрольные работы. Карточки для работы над ошибками. Ответы» Узорова Ольга Васильевна, Нефедова Елена Алексеевна — описание книги | Академия начального образования

Алтайский край

Альметьевск

Амурская область

Ангарск

Астрахань

Белгород

Братск

Брянск

Владивосток

Владимирская область

Волгоград

Волгоградская область

Воронеж

Воронежская область

Грозный

Екатеринбург

Ивановская область

Иркутск

Кабардино-Балкарская Республика

Калужская

Кемерово

Кемеровская область

Киров

Кострома

Краснодарский край

Красноярск

Красноярский край

Курганская

Курск

Липецк

Лиски

Москва

Московская область

Нижегородская область

Нижний Новгород

Нижний Тагил

Нововоронеж

Новосибирск

Новосибирская область

Омск

Оренбург

Оренбургская область

Орловская область

Пенза

Пермский край

Пермь

Поворино

Приморский край

Республика Адыгея

Республика Башкортостан

Республика Бурятия

Республика Крым

Республика Мордовия

Республика Северная Осетия — Алания

Республика Татарстан

Республика Тыва

Республика Хакасия

Россошь

Ростов-на-Дону

Ростовская область

Рязань

Самара

Самарская область

Саратов

Саратовская область

Свердловская область

Севастополь

Смоленск

Ставрополь

Ставропольский край

Старый Оскол

Тамбов

Тамбовская область

Тверь

Томск

Тула

Тулун

Тюмень

Удмуртская Республика

Ульяновск

Ульяновская область

Усолье‑Сибирское

Ханты-Мансийский автономный округ

Челябинск

Челябинская область

Чувашская Республика

Энгельс

Ямало-Ненецкий автономный округ

Ярославль

Ярославская область

3 класс.

Моро. Учебник №1. Ответы к стр. 67

Числа от 1 до 100

Умножение и деление (продолжение)
Площадь. Единицы площади
Ответы к стр. 67

1. Из 12 м ткани портной сшил 6 одинаковых детских костюмов. Сколько метров ткани потребуется на 10 таких костюмов? на 7 костюмов?

1) 12 : 6 = 2 (м) — расход ткани на один костюм
2) 2 • 10 = 20 (м) — расход ткани на 10 костюмов
3) 2 • 7 = 14 (м) — расход ткани на 7 костюмов
О т в е т: на 10 костюмов потребуется 20 м ткани; на 7 костюмов — 14 м ткани.

2. Для ремонта квартиры купили 4 банки краски, по 3 кг каждая. Сколько килограммов краски купили?
Составь две обратные задачи и реши их.

Р е ш е н и е:
4 • 3 = 12 (кг)
О т в е т: купили 12 кг краски.

Обратные задачи:

1) Для ремонта квартиры купили 12 кг краски в 4-х банках. Сколько килограммов было краски в каждой банке?

12 : 4 = 3 (кг)
О т в е т: в каждой банке было по 3 кг краски.

2) Для ремонта квартиры купили 12 кг краски по 3 кг в каждой. Сколько банок краски купили?

12 : 3 = 4 (б.)
О т в е т: купили 4 банки краски.

6. 9 • (38 — 30) = 72 8 • 7 + 5 • 6 = 86
65 — (49 — 19) = 35 9 • 9 — 28 : 7 = 77
28 + 45 : 5 = 37 63 : 7 + 54 : 6 = 18

7 • (100 — 91) = 63
6 • (75 — 65) = 60
7 + 36 : 4 = 16

7. Коля, Дима и Саша собрали вместе 30 грибов. Дима нашёл в 2 раза больше грибов, чем Коля, а Коля — в 3 раза меньше, чем Саша. Сколько грибов нашёл каждый из них?
Сделай чертёж к задаче и реши её.

Из рисунка видно, что Саша нашёл половину всех грибов. А из условия задачи известно, что Коля нашёл грибов в 3 раза меньше, чем Саша. Дима же нашёл грибов в 2 раза больше, чем Коля.
1) 30 : 2 = 15 (г.) — нашёл Саша
2) 15 : 3 = 5 (г.) — нашёл Коля
3) 5 • 2 = 10 (г.) — нашёл Дима
О т в е т: Коля нашёл 5 грибов, Дима — 10 грибов, а Саша — 15 грибов.

8. В альбоме для раскрашивания было 25 рисунков. В первый день Оля раскрасила несколько рисунков, во второй — на 3 рисунка больше, чем в первый. После этого 18 рисунков остались нераскрашенными. Сколько рисунков Оля раскрасила в первый день?

1) 25 — 18 = 7 (р.) — Оля раскрасила за 2 дня
2) 7 — 3 = 4 (р.)
3) 4 : 2 = 2 (р.)
О т в е т: в первый день Оля раскрасила 2 рисунка.

9. Расставь скобки так, чтобы равенства были верными.

(7 + 2) • 9 — 4 = 77 9 + 18 : (3 + 6) =11
7 + 2 • (9 — 4) = 17 (9 + 18) : 3 + 6 =15

Найди площадь листа картона квадратной формы, длина стороны которого 7 дм.

7 • 7 = 49 дм²

ЗАДАНИЕ НА ПОЛЯХ:

РЕБУСЫ:

_—97 + 27
38 57
59 84

ГДЗ по математике. Учебник. 3 класс. Часть 1. Моро М. И., Бантова М. А., Бельтюкова М. А., Волкова С. И., Степанова С. В.

Математика. 3 класс

3 класс. Моро. Учебник №1. Ответы к стр. 67

4.3 (85.51%) от 185 голосующих

рабочих листов по математике для учащихся 3-х классов.

Рабочие листы для 3-х классных задач

Мы создали широкий выбор печатных листов с задачами по математике для учащихся 3-х классов. Математические текстовые задания помогают учащимся углубить понимание математических понятий, связывая математику с повседневной жизнью.

Эти рабочие листы лучше всего использовать после того, как студент изучит основной навык; например, наши рабочие листы задач «сложение по столбцам» не следует пытаться использовать, пока учащиеся не научатся добавлять в столбцы.

Во многие из наших текстовых задач мы намеренно включаем лишние данные, чтобы учащимся нужно было внимательно прочитать и обдумать вопросы, а не просто применять вычислительную схему для решения задач.

Эти рабочие листы задач со словами включают простое сложение, сложение по столбцам и смешанное сложение и вычитание слов.

Эти рабочие листы задач на вычитание для третьего класса охватывают простое вычитание и вычитание из столбцов.

Эти рабочие листы с задачами умножения слов охватывают простое умножение, умножение на 10 и умножение в столбцах, а также смешанное умножение и деление.Учащиеся должны уметь умножать по столбцам, прежде чем решать более сложные задачи.

Эти рабочие листы включают задачи как с простым, так и с длинным разделением слов. Вопросы с длинным разделением относительно простые (числа от 1 до 100), ответы на которые выражаются остатками.

Эти задачи со словами включают определение дробей, а также сложение и вычитание дробей.

Смешанные задачи для 3-го класса

Следующие рабочие листы содержат сочетание задач на сложение, вычитание, умножение и деление 3 степени.Смешивание математических словесных задач — это окончательный тест на понимание математических концепций, поскольку оно заставляет учащихся анализировать ситуацию, а не механически применять решение.

Задачи со смешанными словами — ментальная математика

Простые вычисления, которые можно выполнить в уме.

Задачи со смешанными словами — математика столбцов

Более сложные вычисления, обычно двух- или трехзначные числа.

Задачи со смешанными словами — более простая форма

У этих задач более короткие тексты и нет лишних данных, поэтому основная задача — выбрать, какую из 4 основных операций использовать.

Задачи с измерением слов для 3 класса

Эти задачи со словом объединяют 4 операции с реальными единицами измерения длины, времени, объема и массы.

Проблемы с длиной слова

Задачи о длине и высоте в дюймах, футах, сантиметрах и метрах. Никаких преобразований единиц.

Проблемы со словом времени

Проблемы со словом времени и прошедшего времени; интервалы с точностью до минуты. Преобразование часов в / из минут.

Задачи о массе и весе слов

Масса и вес в унциях, фунтах, граммах и килограммах. Без конвертации единиц.

Проблемы с объемом и емкостью слов.

Объем и вместимость в жидких унциях, чашках, галлонах, миллилитрах и литрах. Без конвертации единиц.

Задачи Word с переменными

Эти задачи для 3-го класса знакомят учащихся с использованием переменных («x, y и т. Д.») Для представления неизвестных. Задачи относительно простые, но упор делается на использование переменных и написание уравнений.

Задачи на слово с переменными (переменная выбирается за ученика)

Написание переменных для решения текстовых задач (ученик выбирает переменную)

Mathwire.com | Решение проблем: Gr. 3-4

Главная | Список от А до Я | Стандарты | Темы

Ресурсы по решению проблем: 3–4 классы

Решение задач: 3-4 классы

Эти задачи предназначены для учащихся 3-4 классов:

Определение числа и числовые операции

Геометрия и измерения

Паттерны и алгебра

Анализ данных и вероятность

Дискретная математика

Рубрики

Ссылки на сайты, посвященные решению проблем

Тестовые площадки

Назад в меню решения проблем

Приют для животных требует, чтобы учащиеся использовали дроби, чтобы выяснить, сколько кошек и собак было доступно для усыновления в приюте для животных.
«Головастики и лягушки» требует от учащихся использовать дроби, чтобы вычислить, сколько головастиков и лягушек было в аквариуме.
В задаче «Хорошая погода» используются положительные и отрицательные целые числа в настройках погоды.
Задача «Игра с большими числами» требует, чтобы учащиеся сравнивали дроби, десятичные дроби и проценты.
Марш муравьев оценивает понимание учащимися концепции умножения как массивов.
Парад третьего класса также оценивает понимание учащимися концепции умножения как массивов.
Конкурс чирлидеров был разработан для оценки понимания учащимися умножения как массива.
Field Trip требует от учащихся решить реальную задачу разделения и решить, как поступить с оставшейся частью.
Большое число-1 требует, чтобы учащиеся расположили цифры так, чтобы образовалось наибольшее возможное 4-значное число, и объясните, откуда они знают, что образовали наибольшее число.
Большое число-2 требует, чтобы учащиеся расположили цифры так, чтобы образовалось наибольшее возможное 4-значное число, и объясните, откуда они знают, что они образовали наибольшее число.
Наибольшая 3-значная сумма предлагает учащимся расположить заданные цифры, чтобы получить наибольшую сумму, и объяснить свои рассуждения.
Наименьшее трехзначное различие предлагает учащимся расположить заданные цифры так, чтобы получить наименьшее различие, и объяснить свои рассуждения.
High-Number Toss — 1 предназначена для измерения понимания учащимися значения разряда, поскольку она используется в одноименной математической игре на каждый день. & nbsp Учащиеся должны быть знакомы с игрой, чтобы успешно решить задачу.
High-Number Toss — 2 предназначена для измерения понимания учащимися разрядов, используемых в одноименной математической игре на каждый день. & nbsp Учащиеся должны быть знакомы с игрой, чтобы успешно решить задачу.
Назови это число — 1 предназначено для измерения понимания учащимися значения разряда, поскольку оно используется в одноименной математической игре на каждый день. & nbsp Учащиеся должны быть знакомы с игрой, чтобы успешно решить задачу.
Назови это число — 2 предназначено для измерения понимания учащимися разряда, используемого в одноименной математической игре на каждый день.& nbsp Учащиеся должны быть знакомы с игрой, чтобы успешно решить задачу.
Pattern Block Fraction Design требует от учащихся заполнить форму узорами, чтобы создать дизайн, отвечающий определенным требованиям. & nbsp Учащиеся также должны написать дробь, описывающую часть общего дизайна, представленную каждым блоком с различным цветовым узором.
Fraction Game имитирует игру Fraction War, но учащиеся должны нарисовать представление каждой фракции и объяснить, кто выиграл, на основе рисунков.

Quilt Square Challenge : Ученики школы Флинн в Перте, Амбой, штат Нью-Джерси, использовали блоки для квилтинга и коврики для квилтинга, чтобы воссоздать образцы блоков лоскутного одеяла 4×4 и 9×9. & nbsp См. «Quilt Square Challenge» на веб-странице Quilts для получения дополнительной информации об этом упражнении и загрузки блоков и циновок для учащихся.
В коробке для печенья учащиеся должны выяснить, в какой коробке поместится больше печенья.
Узорчатая симметрия блоков заставляет учащихся использовать узорные блоки для заливки формы так, чтобы дизайн имел вертикальную или горизонтальную линию симметрии.
Симметрия блока шаблона: учащиеся должны создать дизайн блока шаблона, чтобы удовлетворить заданные условия, включая симметрию линии и количество различных используемых частей блока шаблона.
Узор «Блочный дизайн» (класс 3) требует, чтобы учащиеся создали дизайн, соответствующий указанным критериям.
Узор «Блочный дизайн» (4 класс) требует, чтобы учащиеся создали дизайн, соответствующий указанным критериям.
Координатная геометрия (класс 4) требует, чтобы учащиеся нанесли указанные точки, соединили точки, чтобы сформировать фигуру, а затем ответили на геометрические вопросы о фигуре.
Площадь и периметр — 1 был разработан для оценки понимания учащимися разницы между площадью и периметром.
Площадь и периметр — 2 был разработан для оценки понимания учащимися разницы между площадью и периметром.
Исследование формы было разработано, чтобы помочь учащимся развить идею о том, что две фигуры с одинаковым периметром не обязательно имеют одинаковую площадь и наоборот.
Загоны для домашних животных были разработаны, чтобы помочь учащимся укрепить представления о периметре и площади, поскольку они используют ограждения фиксированной длины для ограждения самого большого загона для любимого питомца.

Гаражная распродажа — это выкройка на основе домино.
Любимые оболочки — это проблема с шаблоном, которую можно решить с помощью изображения или таблицы ввода / вывода.
Осенний парад предлагает учащимся определить узор, образованный треугольными числами.
Marathon Training — это шаблонная задача, которая побуждает учащихся использовать таблицу ввода-вывода для организации данных и решения.
Сбор тыквы — еще одна проблема с шаблоном, которую можно решить с помощью рисунка или таблицы ввода / вывода.предоставлено Шеннон Коллиер, Школа Джозефа К. Карузо, Кинсбург, Нью-Джерси
Бейсбольный сезон — это шаблонная задача, которую легко решить с помощью таблицы значений.
Пособие Энтони обеспечивает дополнительную практику.
Экономия денег-1 требует, чтобы учащиеся проанализировали схему экономии денег, чтобы решить, хватит ли у учащегося денег на покупку нового компакт-диска, который она хочет.
Экономия денег-2 требует, чтобы студенты проанализировали схему экономии денег, чтобы решить, будет ли у студента достаточно денег, чтобы купить новый DVD, который он хочет.

Chapter Books требует от учащихся построить линейный график, а затем определить медианное значение и режим данных.
Carnival Tickets требует, чтобы учащиеся построили линейный график, а затем определили медианное значение и режим данных.
Lucky Draw был разработан, чтобы помочь учащимся развить понятие вероятности. Учащиеся представляют, как разрезают буквы слов и выражений, кладут их в сумку, а затем вычисляют вероятность вытащить разные буквы.
Математика предлагает учащимся вычислить вероятность вытащить из сумки разные буквы «МАТЕМАТИКА».
Задача для третьеклассников использует буквы из «ТРЕТЬИХ ВЫПУСКНИКОВ» и исследует вероятность вытаскивания разных букв из сумки.
Задача «Любимые домашние животные» требует, чтобы учащиеся заполнили итоговую таблицу, ответили на вопросы о данных и создали гистограмму результатов опроса.
В iPod Songs учащиеся должны читать данные в таблице и создавать гистограмму результатов.
Обследование «Любимые планеты» требует, чтобы учащиеся заполнили частотную диаграмму, использовали диаграмму, чтобы ответить на вопросы о максимуме и минимуме, а затем построить гистограмму результатов опроса.
TV Survey — это пример проблемы анализа данных с вопросами, разработанными для каждого уровня Таксономии Блума.
Spinner Game представляет студентам таблицу частоты вращений и требует от студентов создать гистограмму результатов и нарисовать счетчик, который даст эти результаты.& nbsp Учащиеся должны обосновать предложенный счетчик, объяснив, как он соответствует данным.

Lunch Choices исследует комбинации, учитывая различные варианты меню.
Задача Game Day исследует возможные комбинации, когда учащиеся могут выбирать занятия в центрах Game Day.
Number Draw предлагает учащимся составить все возможные числа из трех заданных цифр.
Игра «Нарисовка чисел». Практикуется составление всех возможных трехзначных чисел с использованием трех разных цифр.
Дома в ряду предлагает учащимся использовать упорядоченную систему подсчета, чтобы определить, сколько разных домов можно раскрасить с использованием заданных цветов.
Сколько разных способов написания математики? призывает студентов исследовать закономерности в треугольнике Паскаля, чтобы решить эту проблему.
Дискретные математические комбинации ставят перед учащимися задачу выяснить, сколько различных комбинаций возможно для разных сценариев.
Number Draw был разработан, чтобы помочь студентам изучить комбинации цифр, используемых для образования чисел.
Игра в кости была разработана, чтобы помочь учащимся изучить комбинации цифр для образования чисел в игровой обстановке.
Задача «Забавная прогулка по променаду» требует от учащихся использования логической сетки, чтобы выяснить, чем каждый ребенок хочет заниматься на променаде. & nbsp Для учителей, которые не знакомы с такими логическими задачами, предоставляется организованное пошаговое решение для помощи в использовании этой логической сетки.

Задачи по математике для KidZone

[Уровень 1] [Оценка 2] [3-й степени] [Оценка 4] [5 класс]

Введение:

Задачи Word перечислены по классам, а внутри каждой оценки — по тема. Я всегда нахожу, что предоставление сезонного рабочего листа помогает сохранить мои дочь взволнована своей работой.

Уровни обучения являются ориентировочными — используйте суждение, основанное на способностях и рвении вашего ребенка (моя старшая дочь всегда ставила оценку ниже, тогда как моя младшая дочь кажется оценкой или два выше — иди прикинь). Имейте в виду, что задачи по математике со словами требуются навыки чтения, понимания и математики, чтобы ребенок, хорошо разбирающийся в основные математические уравнения могут оказаться труднее, чем вы ожидаете, столкнувшись с с математическими задачами со словом.

Все задачи со словами динамические (другими словами, они создают новую проблему каждый раз, когда вы их открываете или нажмите «Обновить» в своем браузере). Слова в частном проблема не изменится, но цифры изменятся. Дети, которые борются преобразование словесной задачи в математическое уравнение будет обнадеживающим (создание уверенности), чтобы снова обратиться к одним и тем же словесным подсказкам с разными числа, поэтому рассмотрите возможность печати пары повторений каждой проблемы. В классе вы можете создать проблему для партнеров или группы учащиеся должны решать вместе, а затем воспроизводить то же проблема для детей делать соло.

Со своей старшей дочерью однажды я понял, насколько она боролся с математикой, когда ее не записали в красивом аккуратном уравнении, я часто решали с ней математическую задачу (выполняя большую часть работы я), а затем предоставил ей несколько повторений той же проблемы с разные числа для нее, чтобы сделать соло. Через несколько недель она смог сделать их без прохождения мамы. Она одна из те ребята, которые говорят: «Это слишком сложно!» довольно быстро так укрепление доверия важно — если она думает, что не может что-то сделать она не может — если думает, что может что-то сделать.Теперь как сделать Я убеждаю ее, что она МОЖЕТ содержать свою комнату в чистоте? * смеяться *

Общие задачи со словами для 1 класса

— Мешки с фасолью
— Ведра
— Собачьи кости
— Время в школу (рисунок предложения)
Тематические задачи со словами для 1 класса
Примечание: проблема возникает с новыми числами каждый раз, когда вы нажимаете

Задачи со словами 2 степени

Тематические задачи со словами для 2 класса
Примечание: проблема возникает с новыми числами каждый раз, когда вы нажимаете

Задачи со словом 3 степени

Тематические задачи со словами для 3 класса
Примечание: проблема возникает с новыми числами каждый раз, когда вы нажимаете

Задачи 4 класса

Тематические задачи со словами для 4 класса
Примечание: проблема возникает с новыми числами каждый раз, когда вы нажимаете

Задачи 5 класса

Тематические задачи со словами для 5 класса
Примечание: проблема возникает с новыми числами каждый раз, когда вы нажимаете

Иллюстративная математика

3-й степени

3.

3.OA.A. Представляйте и решайте задачи, связанные с умножением и делением.

3.OA.A.1. Интерпретируйте произведения целых чисел, например, интерпретируйте $ 5 \ times 7 $ как общее количество объектов в 5 группах по 7 объектов в каждой. Например, опишите контекст, в котором общее количество объектов может быть выражено как $ 5 \ times 7 $.

Пока нет задач, иллюстрирующих этот стандарт.

3.OA.A.2. Интерпретируйте целые частные целых чисел, например, интерпретируйте $ 56 \ div 8 $ как количество объектов в каждой доле, когда 56 объектов разделены поровну на 8 долей, или как количество долей, когда 56 объектов разделены на равные доли По 8 предметов. Например, опишите контекст, в котором количество акций или групп можно выразить как $ 56 \ div 8 $.

3.OA.A.3. Используйте умножение и деление в пределах 100 для решения задач со словами в ситуациях, связанных с равными группами, массивами и измеряемыми величинами, например.

3.OA.A.4. Определите неизвестное целое число в уравнении умножения или деления, связывающего три целых числа. Например, определить неизвестное число, которое делает уравнение истинным в каждом из уравнений $ 8 \ times? = 48 $, $ 5 = \ boxvoid \ div 3 $, $ 6 \ times 6 =? $

3.OA.B. Поймите свойства умножения и взаимосвязь между умножением и делением.

3.OA.B.5. Применяйте свойства операций как стратегии умножения и деления. Примеры: Если известно $ 6 \ times 4 = 24 $, то известно также $ 4 \ times 6 = 24 $. (Коммутативное свойство умножения.) $ 3 \ times 5 \ times 2 $ можно найти по $ 3 \ times 5 = 15 $, затем $ 15 \ times 2 = 30 $, или по $ 5 \ times 2 = 10 $, затем $ 3 \ times 10 = 30 $. (Ассоциативное свойство умножения.) Зная, что $ 8 \ times 5 = 40 $ и $ 8 \ times 2 = 16 $, можно найти $ 8 \ times 7 $ как $ 8 \ times (5 + 2) = (8 \ times 5) + (8 \ раз 2) = 40 + 16 = 56 $.

3.OA.B.6. Поймите разделение как проблему с неизвестным фактором. Например, найдите $ 32 \ div 8 $, найдя число, которое дает 32 $ при умножении на 8 $.

Пока нет задач, иллюстрирующих этот стандарт.

3.OA.C. Умножаем и делим в пределах 100.

3.OA.C.7. Плавно умножайте и делите в пределах 100, используя такие стратегии, как взаимосвязь между умножением и делением (например,g., зная, что $ 8 \ times 5 = 40 $, человек знает $ 40 \ div 5 = 8 $) или свойства операций. К концу 3 класса выучить по памяти все произведения двух однозначных чисел.

3.OA.D. Решайте задачи, связанные с четырьмя операциями, а также выявляйте и объясняйте закономерности в арифметике.

3.OA.D.8. Решите двухэтапные задачи со словами, используя четыре операции. Представьте эти проблемы, используя уравнения с буквой, обозначающей неизвестную величину.

3.OA.D.9. Определите арифметические шаблоны (включая шаблоны в таблице сложения или таблице умножения) и объясните их, используя свойства операций. Например, заметьте, что четырехкратное число всегда четно, и объясните, почему четырехкратное число можно разложить на два равных слагаемых.

3.NBT. 3 класс — Число и операции в десятичной системе счисления

3.NBT.A. Используйте понимание разрядов и свойства операций для выполнения многозначной арифметики.

3.NBT.A.1. Используйте расстановку знаков для округления целых чисел до ближайших 10 или 100.

3.NBT.A.2. Свободно складывайте и вычитайте в пределах 1000, используя стратегии и алгоритмы, основанные на разрядах, свойствах операций и / или взаимосвязи между сложением и вычитанием.

3.NBT.A.3. Умножайте однозначные целые числа на кратные 10 в диапазоне от 10 до 90 (например, $ 9 \ times 80 $, $ 5 \ times 60 $), используя стратегии, основанные на разрядах и свойствах операций.

3. Н.Ф. 3 класс — Число и операции — Дроби

3. Н.Ф.А. Развивайте понимание дробей как чисел.

3.NF.A.1. Под дробью $ 1 / b $ понимается количество, образованное 1 частью, когда целое делится на $ b $ равных частей; Под дробью $ a / b $ понимается количество, образованное частями $ a $ размером $ 1 / b $.

3.NF.A.2. Дробь понимается как число на числовой прямой; представляют дроби на числовой линейной диаграмме.

3.NF.A.2.a. Изобразите дробь $ 1 / b $ на числовой линейной диаграмме, определив интервал от 0 до 1 как целое и разделив его на равные части $ b $. Помните, что каждая часть имеет размер $ 1 / b $ и что конечная точка части, основанная на 0, находится на числовой строке с числом $ 1 / b $.

Пока нет задач, иллюстрирующих этот стандарт.

3.NF.A.2.b. Изобразите дробь $ a / b $ на числовой линейной диаграмме, отметив $ a $ lengths $ 1 / b $ с 0.

Пока нет задач, иллюстрирующих этот стандарт.

3.NF.A.3. Объясните эквивалентность дробей в особых случаях и сравните дроби, рассуждая об их размере.

3.NF.A.3.a. Считайте две дроби эквивалентными (равными), если они одного размера или одинаковые точки на числовой прямой.

3.NF.A.3.b. Распознавайте и генерируйте простые эквивалентные дроби, например, $ 1/2 = 2/4 $, $ 4/6 = 2/3 $. Объясните, почему дроби эквивалентны, например, используя визуальную модель дробей.

3.NF.A.3.c. Выражайте целые числа как дроби и распознавайте дроби, которые эквивалентны целым числам. Примеры: выразите $ 3 $ в форме $ 3 = 3/1 $; признать, что $ 6/1 = 6 $; поместите $ 4/4 $ и $ 1 $ в одну и ту же точку числовой линейной диаграммы.

Пока нет задач, иллюстрирующих этот стандарт.

3.NF.A.3.d. Сравните две дроби с одним и тем же числителем или одним знаменателем, рассуждая об их размере. Признайте, что сравнения действительны только тогда, когда две дроби относятся к одному и тому же целому. Запишите результаты сравнений с помощью символов $> $, = или $

3.MD. Уровень 3 — Измерения и данные

3.MD.A. Решайте задачи, связанные с измерением и оценкой интервалов времени, объемов жидкости и масс объектов.

3.MD.A.1. Назовите и запишите время с точностью до минуты и измерьте интервалы времени в минутах. Решайте задачи со словами, включая сложение и вычитание временных интервалов в минутах, например, представляя задачу на числовой диаграмме.

3.MD.A.2. Измеряйте и оценивайте объемы и массу жидкости в объектах, используя стандартные единицы: граммы (г), килограммы (кг) и литры (л).

3.MD.B. Представляйте и интерпретируйте данные.

3.MD.B.3. Нарисуйте масштабированный графический график и масштабированную гистограмму для представления набора данных с несколькими категориями. Решайте одно- и двухэтапные задачи «на сколько больше» и «на сколько меньше», используя информацию, представленную в виде масштабированных гистограмм.Например, нарисуйте гистограмму, в которой каждый квадрат гистограммы может представлять 5 домашних животных.

3.MD.B.4. Генерируйте данные измерения, измеряя длину с помощью линейки, отмеченной половинками и четвертью дюйма. Покажите данные, построив линейный график, на котором горизонтальная шкала обозначена соответствующими единицами — целыми числами, половинками или четвертями.

Пока нет задач, иллюстрирующих этот стандарт.

3.MD.C.Геометрические измерения: понять понятия площади и соотнести площадь с умножением и сложением.

3.MD.C.5. Распознавайте площадь как атрибут плоских фигур и поймите концепции измерения площади.

Пока нет задач, иллюстрирующих этот стандарт.

3.MD.C.5.a. Квадрат со стороной 1 единица, называемый «единичный квадрат», считается имеющим «одну квадратную единицу» площади и может использоваться для измерения площади.

Пока нет задач, иллюстрирующих этот стандарт.

3.MD.C.5.b. Плоская фигура, которую можно покрыть без промежутков или перекрытий на $ n $ единиц квадратов, называется площадью $ n $ квадратных единиц.

Пока нет задач, иллюстрирующих этот стандарт.

3.MD.C.6. Измерьте площади, посчитав единичные квадраты (квадратные см, квадратные метры, квадратные дюймы, квадратные футы и импровизированные единицы).

3.MD.C.7. Отнесите область к операциям умножения и сложения.

Пока нет задач, иллюстрирующих этот стандарт.

3.MD.C.7.a. Найдите площадь прямоугольника с целыми числами сторон, выложив его мозаикой, и покажите, что площадь такая же, как и при умножении длин сторон.

3.MD.C.7.b. Умножьте длины сторон, чтобы найти площади прямоугольников с целочисленными длинами сторон в контексте решения реальных и математических задач, и представьте целочисленные произведения в виде прямоугольных областей в математических рассуждениях.

Пока нет задач, иллюстрирующих этот стандарт.

3.MD.C.7.c. Используйте мозаику, чтобы показать в конкретном случае, что площадь прямоугольника с целочисленными длинами сторон $ a $ и $ b + c $ равна сумме $ a \ times b $ и $ a \ times c $. Используйте модели площади для представления свойства распределения в математических рассуждениях.

3.MD.C.7.d. Распознайте область как добавочную. Найдите области прямолинейных фигур, разложив их на неперекрывающиеся прямоугольники и добавив области неперекрывающихся частей, применяя эту технику для решения реальных проблем.

3. MD.D. Геометрические измерения: распознавать периметр как атрибут плоских фигур и различать линейные измерения и измерения площади.

3.MD.D.8. Решение реальных и математических задач, связанных с периметрами многоугольников, включая поиск периметра с учетом длины сторон, поиск неизвестной длины стороны и отображение прямоугольников с одинаковым периметром и разными областями или с одинаковой площадью и разными периметрами.

Пока нет задач, иллюстрирующих этот стандарт.

3.G. 3 класс — Геометрия

3.Г.А. Размышляйте с формами и их атрибутами.

3.G.A.1. Поймите, что формы в разных категориях (например, ромбы, прямоугольники и другие) могут иметь общие атрибуты (например, иметь четыре стороны), и что общие атрибуты могут определять более крупную категорию (например, четырехугольники).

Пока нет задач, иллюстрирующих этот стандарт.

3.G.A.2. Разделите фигуры на части равной площади. Выразите площадь каждой части как единичную долю от целого. Например, разделите фигуру на 4 части с равной площадью и опишите площадь каждой части как 1/4 площади фигуры.

Бесплатные распечатываемые листы по математике для 3 класса

Вы здесь: На главную → Рабочие листы → 3 класс

Это исчерпывающий набор заданий по математике для 3 класса, организованный по таким темам, как сложение, вычитание, мысленная математика, перегруппировка, разряд, умножение, деление, часы, деньги, измерение и геометрия.Они генерируются случайным образом, их можно распечатать в вашем браузере и включать в себя ключ ответа. Рабочие листы подходят для любой математической программы четвертого класса, но особенно хорошо подходят для математической программы IXL для третьего класса.

Рабочие листы генерируются случайным образом каждый раз, когда вы нажимаете на ссылки ниже. Вы также можете получить новый, другой, просто обновив страницу в своем браузере (нажмите F5).

Вы можете распечатать их прямо из окна браузера, но сначала проверьте, как это выглядит в «Предварительном просмотре».Если рабочий лист не умещается на странице, настройте поля, верхний и нижний колонтитулы в настройках страницы вашего браузера. Другой вариант — настроить «масштаб» на 95% или 90% в предварительном просмотре печати. В некоторых браузерах и принтерах есть опция «Печатать по размеру», которая автоматически масштабирует рабочий лист по размеру области печати.

Все рабочие листы содержат ключ ответа, расположенный на 2-й странице файла.

Ментальное дополнение

Добавить в столбцы

Ментальное вычитание

Вычесть в столбцах

Если вам нужен меньший размер шрифта, больше проблем, больше или меньше места и т. Д.всего сгенерируйте рабочие листы самостоятельно !

Порядок работы

Значение места

Римские цифры

Часы

Деньги — счет монет

Пенни, пятицентовики, десять центов и четвертинки — не более 2,00 долларов США
Пенни, пятак, десять центов и четвертинки — не более 5,00 долларов США
Пенни, пятак, десять центов, четвертак и полдоллара — максимум 5 долларов.00
Пенни, пятицентовики, десять центов, четвертинки и полдоллара — максимум 5 долларов США, показаны в случайном порядке
Пенни, пятицентовики, десять центов, четвертинки и полдоллара — не более 10,00 долларов США

Четыре обычные монеты плюс банкноты 1 и 5 долларов — средний
Все 5 монет плюс купюры 1, 5 и 10 долларов, показаны в порядке
Все 5 монет плюс купюры 1, 5 и 10 долларов показаны в случайном порядке

Используйте эти страницы для создания таблиц для других валют:

Умножение умножения

Я верю в метод, который я называю структурированным сверлением таблиц умножения. Сначала это не случайно, но студенты практикуют таблицы на основе шаблонов в таблицах — и (ОЧЕНЬ ВАЖНО) они также практикуют таблицы «задом наперед». Таблицы можно использовать для произвольного сверления после начального этапа структурированного бурения.

Пропуск на 2, начиная с 2
Пропуск на 3, начиная с 3
Пропуск на 4, начиная с 4
Пропуск на 5, начиная с 5
Пропустить счет на 6, начиная с 6
Пропустить счет на 7, начиная с 7
Пропуск на 8, начиная с 8
Пропустить счет на 9, начиная с 9

Таблица умножения 2 и 3
Таблица умножения 5 и 10
Таблица умножения 4 и 6
Таблица умножения 7 и 8
Таблица умножения 9 и 3
Таблицы умножения 7, 8 и 9

Таблицы 2-5 практика
Таблицы 6-9 на практике
Таблицы 2-10 практика
Таблицы 2-12 практика

Таблица умножения 2-10, пропущенный множитель
Таблица умножения 2-12, пропущенный множитель

Умножить целые десятки на однозначные числа
Умножить на целые десятки, пропущенный коэффициент

См. Также видео ниже, в котором объясняется метод «структурированной детализации» для изучения таблиц умножения.

Психологическое отделение

Геометрия

Самостоятельно изготовить рабочие листы площади / периметра

Единицы измерения

Преобразование единиц измерения не включено в Common Core Стандарты для 3-го класса, поэтому они не являются обязательными.

Метрические единицы

Дроби

Рабочие листы для преобразования смешанных чисел в дроби и наоборот необязательно, так как это не требуется, чтобы ученик мог делать это в 3-м классе без наглядной модели.

Если вы хотите иметь больший контроль над такими параметрами, как количество задач, размер шрифта, интервал между проблемами или диапазон чисел, просто щелкните по этим ссылкам, чтобы самостоятельно использовать генераторы рабочих листов:

Стратегии решения задач со словами для учащихся K – 4 классов [Бесплатные шаблоны]

Стратегии решения математических задач со словами следует начинать еще в детском саду или в первом классе! Поскольку в последние годы чтению научной литературы уделяется более пристальное внимание, мы можем рассматривать текстовые задачи как часть жанра научной литературы. Загрузки для сегодняшней публикации включают несколько шаблонов или графических органайзеров, которые помогут студентам найти связь между задачами со словами и уравнениями, которые представляют эти проблемы.

Как учитель математики, я много раз слышал, что «мы все учителя чтения», и этот пост покажет, как связаны эти две области, как математика, так и чтение, поскольку ученики создают представления, чтобы помочь им перейти от слов к уравнениям и наоборот. Кроме того, возьмите мои загружаемые шаблоны для нескольких представлений ниже! Используя эти шаблоны для разработки уроков, вы можете обратиться ко многим Стандартам математической практики, которые лежат в основе стратегий решения словесных задач.

SMP 1: разбираться в проблемах и настойчиво их решать
SMP 2: Размышляйте абстрактно и количественно
SMP 4: Модель с математикой
SMP 7: Найдите и используйте структуру

Манипулятивное и визуальное представление математических словесных задач тесно связаны. Эти представления представляют собой стратегии решения проблем, которые могут использовать студенты. Я надеюсь, что вы терпите меня, когда я расскажу немного о том, что я узнал об обучении студентов с помощью манипуляций и репрезентаций.В 1960-х Джером Брунер ввел термины активный, иконический и символический, чтобы описать, как ученики продвигаются от использования манипуляторов к созданию рисунков, основанных на манипуляциях, к использованию только чисел и символов. Сегодня мы можем назвать эти шаги конкретными, репрезентативными (полубетонными) и абстрактными. Singapore Math использует термины конкретный, графический и абстрактный. Все эти три набора терминов относятся к одной и той же основной стратегии мастерского использования манипуляторов для демонстрации математической идеи, затем ученики излагают эту идею с помощью бумаги и карандаша (повторно представляют ее) и, наконец, используют только числа и символы для представляют это.

Я бы посоветовал студентам сначала поработать с такими манипуляторами, как счетчики плюшевых мишек, маленькие кубики или даже бобы. Это помогает показать взаимосвязь между ситуациями, о которых учащиеся читают в словесной задаче. Лучше всего, чтобы они использовали шаблон для представления своей идеи, используя десятикратную рамку, числовую связь, массив или модель области и ленточную диаграмму (полубетонные, графические или графические изображения). Наконец, они поймут значение уравнения (абстрактное или символическое представление), когда напишут его.

Word Стратегии решения задач для студентов

Если вы ищете стратегии решения математических задач со словами в детском саду до 4-го класса, вы найдете загружаемые ниже шаблоны очень полезными. Используя шаблоны, вы можете дать учащимся стратегии чтения текстовых задач и создания представлений для их решения или даже дать им представление и предложить им создать текстовые задачи. Используйте эти загружаемые шаблоны, чтобы дать учащимся стратегии решения словесных задач, включающих сложение, вычитание, умножение и деление.Распечатайте их и используйте сегодня в своем классе!

Детский сад и 1 класс — добавление

Ожидается, что в младших классах ученики только прибавят. Типичная проблема со словами может быть такой: «У Криса три апельсина и два яблока. Сколько фруктов у Криса вместе? » Студенты могут моделировать задачу, используя кубики разного цвета. В загружаемом шаблоне есть место для вопроса, после чего учащиеся могут рисовать на основе своих манипуляций. Ключевые полуабстрактные представления для этих студентов — десять рамок и числовые связи.В частности, с числовыми связями учащиеся должны думать о частях и итогах. Наконец, ученики пишут дополнительное предложение.

Для добавления доступны два шаблона. В первом есть одна десятка кадров, предназначенная для детского сада, где ученики добавляют только в пределах десяти. Во втором есть две десятичные рамки, ориентированные на первый класс, где ученики складывают в пределах двадцати. Студентов продвинутого уровня можно подтолкнуть к представлению своих дополнительных предложений с помощью числовой линии, но это не входит в эту загрузку.

1 и 2 классы — сложение и вычитание

По мере того, как ученики переходят в 1-й и 2-й классы, они узнают о взаимосвязи между сложением и вычитанием. Концептуально это отличается от ранней работы с простым добавлением. Стратегии решения проблем со сложением слов с двумя слагаемыми могут быть шаблонными. Два числа в словарной задаче необходимо сложить, но когда учащийся сталкивается с текстовой задачей с отсутствующей частью, у него должны быть стратегии и представления, чтобы думать о частях и целых.

В шаблоне для сложения и вычитания вы найдете числовые связи и ленточную диаграмму. Каждый шаблон имеет рамку с двумя числовыми связями, одна с удаленной «целой», а другая с одной из «частей». Студенты должны прочитать задачу и решить, является ли проблема типом отсутствующей части или отсутствующей целой. Вот где нам нужно связать чтение с математикой. Точно так же учащиеся должны заполнить ленточную диаграмму, используя идеи части и целого, но на этот раз используя знак «?» или буква как переменная, обозначающая неизвестное.

Наконец, учащиеся должны написать хотя бы одно предложение сложения или вычитания, чтобы представить проблему с помощью «?» или переменная для неизвестного. Затем они могут написать числовое предложение, показывающее «решение», вместо вопросительного знака или переменной. Студентов продвинутого уровня можно подтолкнуть к представлению числовых предложений с помощью числовой строки, но это не входит в эту загрузку.

Оценка 3 и 4 — умножение и деление

Опираясь на работу во втором классе, учащиеся 3 и 4 классов должны применять стратегии решения словесных задач, включающие умножение и деление.Эти задачи требуют другого представления, чем стратегии математических задач со словами, включающие сложение и вычитание.

Загружаемый шаблон для классов 3 и 4 включает место для модели массива, модели области и ленточной диаграммы. Для ясности: учащиеся могут представлять задачи умножения и деления слов, используя любое из этих трех представлений:

Вы можете видеть, что эта серия абстрактных представлений умножения и деления переходит от более конкретных (полуабстрактных) версий, где вы можете считать точки или квадраты, к более абстрактным версиям, где учащиеся переходят от счета к поиску решений. Это также помогает студентам на начальном этапе использовать переменные для представления неизвестных, поскольку они могут пометить отсутствующие части модели области или массива буквой.

В последнем поле загружаемого шаблона учеников просят написать уравнение, используя переменную или вопросительный знак для неизвестного, а затем «решить» его. Под решением я подразумеваю не использование алгебраических шагов (т. Е. Деление обеих сторон на три), а вместо этого просто написать «x = 7» в случае примера, приведенного непосредственно выше.Учащиеся могли использовать любую форму рассуждений, в том числе вернуться к использованию физических счетчиков и разделить их на равные группы.

Как стандарты математической практики соотносятся с использованием шаблонов

Я хочу поделиться некоторыми мыслями о том, как эти загружаемые шаблоны можно использовать для разработки стратегий учащихся по решению математических задач со словами и использования Стандартов математической практики (SMP).

SMP 1: разбираться в проблемах и настойчиво их решать.

Когда студентов просят составить схему, они должны четко понимать, что такое части и целое. Предоставление им таких представлений, как числовые связи, модели площадей и массивов или ленточные диаграммы, помогает им понять проблемы и взаимосвязи элементов, которые они обнаруживают при чтении слова «проблема».

SMP 2: Размышляйте абстрактно и количественно.

Когда учащиеся создают представление, такое как в Загрузке 4 (3 прямоугольника «x» равны 21), это абстрактное представление.Он ничего не говорит о том, в чем проблема. Когда учащиеся читают задачу о количестве (три игрушки общей стоимостью 21 доллар) и составляют ленточную диаграмму, они переходят от количеств к абстракциям. Еще один способ использования этих шаблонов — заполнить ленточную диаграмму (или модель массива или области) и попросить учащихся заполнить остальные поля. Другими словами, ученики будут создавать свои собственные задачи с текстом из ленточной диаграммы. Они начинают с абстрактного представления и приходят к количественной идее (это может быть 21 яблоко и три человека или 21 шоколад и три коробки и т. Д.).

SMP 4: Модель с математикой.

Такие модели, такие как модели с областями и ленточные диаграммы, если они будут введены на раннем этапе, помогут учащимся, когда они используют модели с областями в старших классах для моделирования более сложных задач.

SMP 7: Ищите и используйте структуру.

Чтение задач со словами, а затем создание представлений с использованием шаблонов поможет учащимся найти ключевые слова и их отношение к структуре частей и целых, строк и столбцов, факторов, итогов и делителей.Просмотр общих базовых структур с использованием числовых связей, десяти рамок, моделей площадей и массивов, а также ленточных диаграмм помогает укрепить общие базовые структуры, которые появляются в различных текстовых задачах.

Резюме

Загрузите и используйте мои бесплатные шаблоны, чтобы помочь студентам найти связь между задачами со словами и уравнениями, которые представляют эти проблемы. Когда вы это сделаете, вы научите учащихся использовать «Стандарты математической практики», описанные выше, давая им возможность представить себе в голове проблемы со словами и создать представления, которые показывают взаимосвязь задействованных количеств.

Задачи по математике для 3-го класса

Задачи со словами дают учащимся возможность применить свои математические навыки в реальных ситуациях. Слишком часто дети, способные решать числовые задачи, теряются, когда сталкиваются с проблемой со словами. Одними из лучших проблем для работы являются те, в которых неизвестный фактор находится либо в начале, либо в середине проблемы. Например, вместо того, чтобы сказать: «У меня 29 воздушных шаров, и ветер унес восемь из них», а затем спросить: «Сколько у меня осталось?» попробуйте вместо этого что-нибудь вроде этого: «У меня было много воздушных шаров, но восемь из них ветер унес.Теперь у меня остался только 21 воздушный шарик. Сколько у меня было с самого начала? »Или:« У меня было 29 воздушных шаров, но ветер унес некоторые прочь, а сейчас у меня только 21 ». Сколько воздушных шаров унес ветер? »

Примеры проблем со словами

kali9 / Getty Images

Как учителя и родители, мы часто очень хорошо умеем создавать или использовать словесные задачи, в которых неизвестное значение находится в конце вопроса. К сожалению, этот тип проблем может оказаться слишком сложным для маленьких детей.Изменяя положение неизвестного, вы можете создавать задачи, которые будет легче решать начинающим математикам.

Еще один тип проблемы, который отлично подходит для молодых учеников, — это двухэтапная задача, которая требует от них решить одну неизвестную проблему, прежде чем решать другую. Освоив базовые задачи со словом, молодые студенты могут выполнять задачи из двух (и трех), чтобы работать над более сложными концепциями. Эти проблемы помогают учащимся научиться обрабатывать и связывать сложные наборы информации.Вот некоторые примеры:

В каждом ящике апельсинов 12 рядов по 12 апельсинов. Директор школы хочет купить достаточно апельсинов, чтобы каждый ученик получил по апельсину. В школе 524 ученика. Сколько ящиков нужно купить директору?
Женщина хочет посадить тюльпаны в своем цветнике. У нее достаточно места, чтобы посадить 24 тюльпана. Тюльпаны можно купить пучками по пять штук по цене 7 долларов за пучок или по 1,50 доллара за штуку. Женщина хочет тратить как можно меньше денег.Что ей делать и почему?
421 ученик Eagle School отправляется в зоопарк. В каждом автобусе 72 места. Также в поездку отправляются 20 учителей, чтобы наблюдать за учениками. Сколько нужно автобусов, чтобы все ученики и учителя могли добраться до зоопарка?

Студентам часто нужно перечитывать вопрос, чтобы убедиться, что у них есть вся необходимая информация. Их также следует побуждать прочитать вопрос еще раз, чтобы убедиться, что они действительно понимают, для чего им задается вопрос.