Презентация на тему: «Пересечение и объединение множеств» | Презентация к уроку по математике (3 класс) на тему:
Слайд 1
Пересечение и объединение множеств. Кунделева Оксана Евгеньевна Учитель начальных классов МБОУ НОШ № 279 г. Гаджиево, Мурманской области, 2012 г.Слайд 2
Цели занятия формировать представление об объединении и пересечении двух множеств учить находить на «карте множеств» область множества, которое является пересечением или объединением двух множеств учить определять принадлежность элементов множеству, которое является пересечением и объединением двух множеств учить определять характер отношений между двумя заданными множествами (пересечение, не пересекаются, объединение)
Слайд 3
Что такое множество? Множество — это группа предметов, объектов или существ.
Слайд 4
Назовите элементы множества: “Месяцы года” “Времена года” “Материки” “Летающие бегемоты” Многоугольники
Слайд 5
Оса Летучая мышь ворона пингвин Бабочка синица страус воробей Прочитайте названия птиц. Обведите это множество. Сделайте надпись внизу: “Птицы”. ПТИЦЫ Прочитайте названия животных, которые умеют летать. Обведите это множество, сделайте надпись вверху: ”Умеют летать”. умеют летать Сколько элементов оказалось на пересечении двух множеств , т.е. одновременно в двух множествах? Почему?
Обведите это множество. Сделайте надпись внизу: “Птицы”. ПТИЦЫ Прочитайте названия животных, которые умеют летать. Обведите это множество, сделайте надпись вверху: ”Умеют летать”. умеют летать Сколько элементов оказалось на пересечении двух множеств , т.е. одновременно в двух множествах? Почему?
Слайд 6
Пересечение множеств общая часть множеств Если в названии множества есть слово «И» , то каждый его элемент должен находиться на ПЕРЕСЕЧЕНИИ двух множеств – жить одновременно в двух странах . !
Слайд 7
Объединение множеств Если в названии множества есть слово «ИЛИ» , то элемент может быть в любом месте на территории двух стран — ОБЪЕДИНЕНИИ — жить хотя бы в одной из них. ! ! ! !
Слайд 8
Что такое подмножество? Подмножество – это часть множества, входящее в данное множество.
Слайд 9
Физкультминутка Раз – согнуться, разогнуться, Два – нагнуться, потянуться, Три – в ладоши три хлопка, Головою три кивка. На четыре руки шире, Пять, шесть – тихо сесть, Семь, восемь – лень отбросим.
Слайд 10
Множество обитателей моря Множество млекопитающих Начерти множества:
Слайд 11
Начерти множества: Множество птиц Множество рыб
Слайд 12
В квадрате живут чётные числа. В треугольнике живут двузначные числа. Впиши правильно каждое число. Закрась на рисунке область, где живут чётные двузначные числа. 2, 47, 16, 8, 17, 32, 6, 53 2 47 16 8 17 32 53 6
Слайд 13
Найди обозначение каждого множества в таблице и закрась круги на рисунке. Множества: прямоугольников четырёхугольников многоугольников квадратов Сколько множеств обозначено кругами? Какое множество самое большое? Каким цветом нужно закрасить самый большой круг? Какое самое большое из оставшихся?
Слайд 14
Множества: животных Зверей Рыб Птиц Растений Чайка Лиса Айсберг Жираф Сосна Река Тюльпан Муравей Камбала Найди и расположи элементы множеств в фигурах на рисунке: впиши первую букву каждого слова из списка
Слайд 15
Ч К М Т Р С Ж А Л
Слайд 16
Запомни! Множества не пересекаются Множества не пересекаются: Одно множество является подмножеством другого Одно множество является подмножеством другого: Множества пересекаются: Множества объединяются:
Слайд 17
До встречи на следующем уроке!!!
Слайд 18
А. В. Горячев, К.И. Горина и др. Информатика в играх и задачах, 3 класс, Методические рекомендации для учителя, М., « Баллас », 2004 А.В. Горячев, К.И. Горина и др. Учебник «Информатика в играх и задачах», 3 класс, часть 2, М., « Баллас », 2004 http://festival.1september.ru/articles/505635/ Урок информатики по теме «Множество. Подмножество. Пересечение множеств» Щепина Зинаида Николаевна , учитель начальных классов Используемая литература
В. Горячев, К.И. Горина и др. Информатика в играх и задачах, 3 класс, Методические рекомендации для учителя, М., « Баллас », 2004 А.В. Горячев, К.И. Горина и др. Учебник «Информатика в играх и задачах», 3 класс, часть 2, М., « Баллас », 2004 http://festival.1september.ru/articles/505635/ Урок информатики по теме «Множество. Подмножество. Пересечение множеств» Щепина Зинаида Николаевна , учитель начальных классов Используемая литература
Урок математики в 3 классе на тему «Пересечение множеств»
Тема урока: «Пересечение множеств»
Цель урока: сформировать представление о понятии «пересечение» множеств.
Задачи урока:
узнать какую часть множеств называют «пересечением»;
узнать какие элементы множеств входят в пересечение»;
научиться понимать, читать и составлять данные высказывания;
научиться изображать пересечение множеств при помощи графической модели.

Ход урока:
Орг. момент.
(Слайд 1)
Учитель
Вот и солнышко с утра,
И в душе у нас весна!
Мы начнем урок с улыбок.
Выполним всё без ошибок
Учащиеся
Мы пришли сюда учиться,
Не лениться, а трудиться.
Слушаем внимательно,
Работаем старательно.
— Я рада, что у Вас хорошее настроение. Улыбнитесь друг другу. Я надеюсь, что такое настроение у Вас останется до конца урока и вы будете старательны и внимательны.
— Сейчас урок математики.
— Давайте повторим то, что мы уже знаем.
Актуализация знаний учащихся.
— Какой раздел мы начали изучать? (Мы начали изучать раздел «Множества»)
(Слайд 2)
— Что такое множества? (Множество – это группа предметов, объектов или живых существ, собранных вместе)
— Можно ли назвать предметы, на данном рисунке, множеством? (Да, это группа живых существ собранных вместе.)
— Назовите это множество. (Множество бабочек.)
(Слайд 3)
— Дайте общее название данным множествам.
— Из чего состоят множества? (Множества состоят из элементов)
— Что можно сделать с элементами множества? (Посчитать и перечислить их. )
)
— Посчитайте и перечислите элементы множества «Посуда».
— Что означает: «
— А что значит: задать множество? (Это значит назвать общее свойство или признак всех его элементов.)
— Приведите свои примеры, назовите общее свойство каких-либо объектов.
Постановка проблемы и поиск решения.
— Сегодня на уроке мы познакомимся ещё с одним понятием, связанным с множеством предметов.
— Какое множество вы видите? (Множество домов)
— На какие две группы можно поделить множества домов на доске? (Красные дома и желтые дома.)
— Какой основной признак у домов в первом множестве? (Красный цвет. )
)
— У домов второго множества? (Желтый цвет.)
— В нашем необычном городе живет странный архитектор. Кто такой архитектор? Ответы детей.
— Верно. Архитектор – человек проектирующий здания, создающий внешний вид городов.
— В нашем городе он разрешает строить на одной улице только красные дома, а на другой только желтые дома. И живет в нашем городе веселый художник, он захотел построить дом красно-желтого цвета. Давайте поможем нашему художнику. Поставим дом на одну из улиц.
— Можем ли мы поставить этот домик на первую улицу? (Нет, потому, что их общий признак жёлтый цвет, а он желто-красный)
— Можем ли мы поставить этот домик на вторую улицу? (Нет.)
(Дети пытаются выполнить задание сами.)
— Смогли вы выполнить мое задание?
 )
)— Почему? (Потому что на одной улице можно строить только желтые дома, а на другой только красные дома.)
— Какой у нас возникает вопрос? (Куда поставить красно-желтый дом?)
— Давайте вместе будем решать данную проблему.
— Какие признаки имеет наш дом? (Он желтого и красного цвета.)
— На каких улицах он может находится, благодаря своим признакам? (Он должен стоять на красной улице, потому что он красный и на желтой улице, потому что он желтый.)
— То есть он должен находится на обеих улицах одновременно
— А как должны располагаться улицы, чтобы, находясь на одной улице, мы одновременно стояли и на другой улице. В таких местах обычно ставят светофоры. (Улицы должны пересекаться.)
— Итак, какая гипотеза оказалась верной. (Поставить дом на пересечение двух дорог. )
)
— Каждая улица это множество домов, значит, куда мы поставили наш дом.
(На пересечение множеств.)
— Предположите, какова будет тема нашего урока. (Пересечение множеств)
(Слайд 4)
— Цель нашего урока: сформировать представление о понятии «пересечение» множеств.
— А вот задачи урока давайте попробуем сформулировать вместе. На какие вопросы по данной теме вы бы хотели получить ответы? Ответы детей.
(Слайд 5)
— Задачи урока:
узнать какую часть множеств называют «пересечением»;
узнать какие элементы множеств входят в пересечение»;
научиться понимать, читать и составлять данные высказывания;
научиться изображать пересечение множеств при помощи графической модели;
— Оценивать свою работу на уроке вы будете при помощи оценочных листов. Посмотрите на вопросы в них. Они соответствуют задачам нашего урока. Если вы будите внимательны и старательны на уроке, то и оцените себя по достоинству.
Посмотрите на вопросы в них. Они соответствуют задачам нашего урока. Если вы будите внимательны и старательны на уроке, то и оцените себя по достоинству.
— К нашим домикам мы вернёмся в конце урока и проверим, смогли ли мы решить поставленные перед собой задачи.
ФИЗМИНУТКА ДЛЯ ГЛАЗ.
— Давайте приготовим наши глазки для дальнейшей работа, проведём физминутку для глаз.
- «Открытие» новых знаний.
Работа с множествами (Слайд 6)
— Приступаем к открытию новых знаний.
— Перед вами два множества и элементы множества. Посмотрите внимательно на элементы множества.
— Дайте названия данным множествам по цвету и материалу изготовления. (Множество зелёных объектов и множество деревянных объектов)
— Давайте распределим данные объекты по множествам.
— Что вы заметили? (Что некоторые объекты, а именно карандаш и кубик вошли и в первое и во второе множество.)
— По свойствам эти предметы подходят И к множеству деревянных предметов И к множеству зелёных предметов. Они являются общими для этих двух множеств.
— Эти элементы являются общими и для первого и для второго множества.
— Поэтому они находятся в пересечении множеств.
(Слайд 8)
— Дайте названия данным множествам.
(1 – зеленые объекты; 2 – деревянные объекты.)
— Попробуйте дать общее название элементам находящимся в пересечении. (зелёные И деревянные объекты)
Вывод.

— Так какую часть множеств называют пересечением? (Общую часть множеств называют пересечением.)
— Это мы с вами пришли к такому выводу.
Работа с учебником с.50— Давайте проверим верно ли наше предположение. Прочитаем в учебнике сообщение с зелёным восклицательным знаком. (Учащиеся читают)
— Совпало ли наше предположение с выводами в учебнике? (Да.)
(Слайд 9)
— Давайте ещё раз проговорим, что называют пересечением? (Общую часть множеств называют пересечением.)
Сообщение учителя со слайда
Если в названии множества есть слово «И», то каждый его элемент должен находиться на ПЕРЕСЕЧЕНИИ двух множеств – жить одновременно в двух странах.
Знакомство с графическим обозначением.
— Обратите внимание, что графически принято изображать отношения между множествами с помощью кругов. Математики называют их кругами Эйлера, т.к. они изобретены Леонардом Эйлером.
(Слайд 10)
— Леонард Эйлер швейцарский, немецкий и российский математик, внёсший значительный вклад в развитие математики. Он почти полжизни провёл в России, где внёс существенный вклад в становление российской науки.
ФИЗМИНУТКА
Первичное закрепление нового материала .
Игра «Найди пересечение множеств»
(Слайд 11 и 12)
— Какие множества вы видите?
— Какие объекты должны лежать в пересечении множеств?
— Покажите графически.
— Дайте название пересечению множеств.
— Что мы называем пересечением множеств? (Общую часть множеств называют пересечением.)
Работа в парах.
— Возьмите конверты. Прочитайте задание и выполните его.
— Распределите элементы множеств. Назовите каждое множество.
(Слайд 13)
— Посмотрите на слайд, сравните со своей работой.
(Проверка с помощью сигнальных карточек)
Работа в группе.
— А сейчас вы будете работать в группе. У вас на столе лежит карточка с заданием. Вы должны будете показать отношения между множествами, данными в задании. А элементами множеств будут члены вашей команды. Старший группы должен будет объяснить, как группа выполняла задание.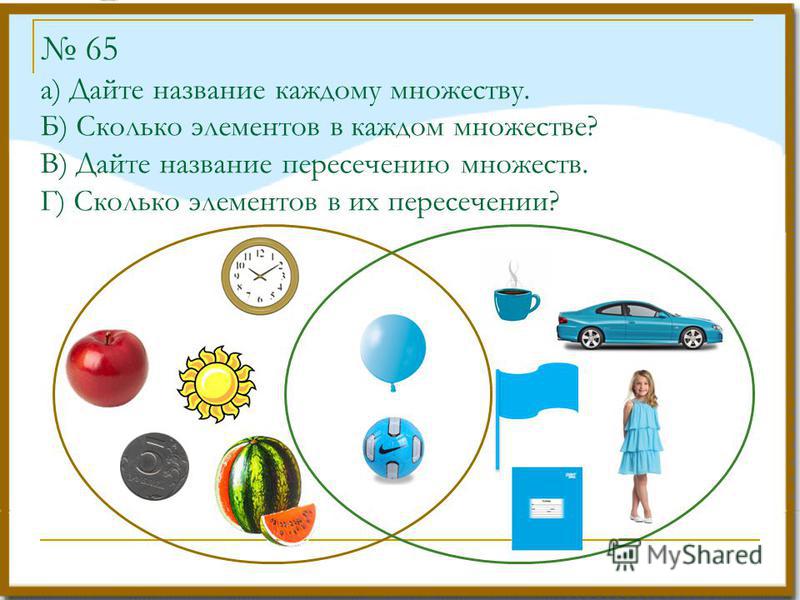
(Ребята распределяют роли в группе.)
— Вы готовы. Сейчас каждая группа будет защищать свою работу, а учащиеся других групп должны будут просигнализировать, согласны ли они с тем, что представляют выступающие. Зелёный сигнал согласны, красный – не согласны.
1 группа
Покажите отношение между множеством девочек и множеством учащихся в брюках. Элементами этих множеств являются учащиеся вашей группы.
Какие элементы множеств находятся в пересечении и почему?
Старший группы поясняет, как выполнили задание.
2 группа
Покажите отношение между множеством мальчиков и множеством блондинов. Элементами этих множеств являются учащиеся вашей группы.
Какие элементы множеств находятся в пересечении и почему?
Старший группы поясняет, как выполнили задание.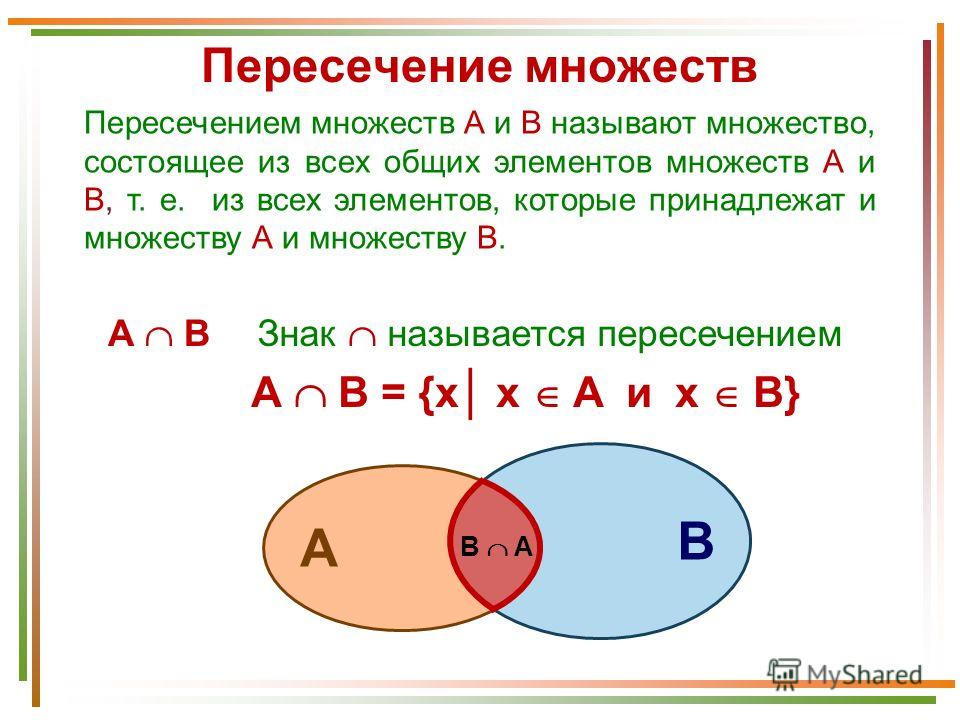
3 группа
Покажите отношение между множеством мальчиков и множеством учащихся в белом. Элементами этих множеств являются учащиеся вашей группы.
Какие элементы множеств находятся в пересечении и почему?
Старший группы поясняет, как выполнили задание.
4 группа
Покажите отношение между множеством девочек и множеством учащихся имя которых начинается на букву «Д». Элементами этих множеств являются учащиеся вашей группы.
Какие элементы множеств находятся в пересечении и почему?
Старший группы поясняет, как выполнили задание.
Индивидуальная дифференцированная работа. (Выбор учащихся по степени сложности)
— У Вас на столах лежат карточки с заданием с красной, зелёной и жёлтой полосой. Эти задания разного уровня сложности. С красной полосой — самое сложное. С зелёной — немного легче. С жёлтой — самое легкое. Выберите каждый для себя конверт и выполните задание. Пишите названия элементов словами.
Эти задания разного уровня сложности. С красной полосой — самое сложное. С зелёной — немного легче. С жёлтой — самое легкое. Выберите каждый для себя конверт и выполните задание. Пишите названия элементов словами.
(Проверка с помощью сигнальных карточек)
— Поднимите красный сигнал, кто выбрал, карточку с красной полосой. Расскажите, как выполняли.
— Поднимите зелёныё сигнал, кто выбрал, карточку с зелёной полосой. Расскажите, как выполняли. Согласны ли с выполнением? Кто взял другие элементы множеств.
— Поднимите жёлтый сигнал, кто выбрал, карточку с жёлтой полосой. Расскажите, как выполняли. Согласны ли с выполнением?
Домашнее задание.
— Решите примеры № 9, с. 51 – в соответствии с заданием.
— А еще у вас на столах есть карточки с синей полосой, в них задание связанное с темой нашего сегодняшнего урока. Вы по желанию, можете взять конверт с заданием и выполнить его дома. Данная работа будет оценена.
Вы по желанию, можете взять конверт с заданием и выполнить его дома. Данная работа будет оценена.
СМЕХОТЕРАПИЯ (воздушный шарик)
— Урок у нас подходит к концу вы наверно устали, давайте проведём сеанс смехотерапии. Я подброшу шарик вверх. Когда он будет находится в воздухе вы смеетесь, а когда он оказывается у меня в руках вы замолкаете.
Итог урока.
— Какая была тема урока? (Пересечение множеств.)
— Давайте вспомним, какие задачи мы ставили перед собой в начале урока.
— Давайте проверим, смогли ли мы решить поставленные перед нами задачи.
(Дети дают ответы по каждому пункту.)
— А сейчас вернёмся к домикам, с которыми мы работали в начале урока.
— Изобразите пересечение множеств при помощи графической модели.
— Распределите элементы множества в данную модель.
— Дайте название каждому из множеств.
Оценивание.
Листы самооценивания.
Рефлексия.
— Давайте подведём итог нашего урока. В этом вам помогут наши предложения (Высказывания детей)
— Я сегодня узнал…
— Я сегодня научился…
— Мне было трудно…
— Мне понравилось…
— Было интересно…
— Могу похвалить себя за то, что …
— Могу похвалить одноклассников за то, что…
— Больше всего мне понравилось….
«Свойства пересечения множеств» 3 класс.
Основные цели:
1) формировать представление о переместительном и сочетательном свойствах операции пересечения множеств;
2) повторить переместительное и сочетательное свойства сложения и умножения, закрепить понятие пресечения множеств;
3) тренировать навыки решения уравнений и задач на приведение к единице.
Познавательные УУД:
использование имеющихся знаний;
исследование учебной задачи;
установление логических, причинно-следственных связей, построение логической цепи рассуждений,
применение знаково-символической схемы.
Регулятивные УУД:
оценивать уровень успешности;
производить контроль своих действий;
определять цель учебной задачи;
планировать свою деятельность, определяемую результатом,
контроль в форме сличения способа действия и его результата с заданным эталоном.
Коммуникативные УУД:
умение слушать и вступать в диалог;
умение правильно выражать свои мысли;
умение контролировать и корректировать действия других;
оформление своей мысли в устной речи;
обоснование своего ответа;
умение ориентироваться в своей системе знаний;
Личностные УУД:
Мыслительные операции, необходимые на этапе проектирования: сравнение, обобщение, аналогия.
Демонстрационный материал:
1) карточки с высказываниями:
«Новое умение — везде найдёт применение».
«Торопись — да не ошибись».
«Повторение — мать учения».
2) карточки с записями:
3) карточки с записью свойств чисел:
а + b = b + а (а + b) + с = а + (b + с)
а · b = b · а (а · b) · с = а · (b · с)
4) карточки для составления эталона:
А ∩ В = В ∩ А
(А ∩ В) ∩ С = А ∩ (В ∩ С)
(А ∩ В) ∩ С = А ∩ (В ∩ С)
Пересечение множеств не зависит
от порядка множеств …
…и от изменения порядка действий.
5) алгоритм рассуждений для вычислений:
Читаю выражение
Определяю свойство, которое можно использовать для упрощения вычислений
Вычисляю
6) эталон для самопроверки к этапу 7:
М ∩ К = К ∩ М Пересечение множеств не зависит
от порядка множеств и порядка
(М ∩ К) ∩ Т = М ∩ (К ∩ Т) действий.
7) «лесенка успеха» Я УЗНАЛ НАУЧИЛСЯ ЗАПОМНИЛ УДИВИЛСЯ
Раздаточный материал:
Листы для выполнения заданий для пробного действия.
Самопроверка к заданиям по выбору (задача)
4 под. – n кв.
6 под. — ? кв.
1 под. — ? кв.
Ответ: 96 квартир в 6 подъездах.
Самопроверка к заданиям по выбору (уравнения)
а
б) 604 – х = 286; 604
х = 604 – 286; 286
х = 318. 318
604 – 286 = 318
318 =318
) х – 394 = 286; 286х = 286 + 394; 394
х = 670 670
286 + 394 = 670
670 = 670
Самопроверка к заданиям по выбору (примеры)
а) (13 + 8 · 4 ) : 5 – (27 : 3 – 0 · 6) = 9 – 9 = 0
0
9
3245 9
б) 40 : (24 : 6) + 7 · (12 – 2 · 2) – 5 · 5 = 10+ 56 – 25 = 10 + 56 – 25 = 41
4 4 25
10 56 8
Ход урока:
1. Мотивация к учебной деятельности.
Мотивация к учебной деятельности.
Цель:
1) создать условия для возникновения у учащихся внутренней потребности включения в учебную деятельность («хочу») через создание ситуации, вызывающей интерес;
2) организовать деятельность учащихся по установке тематических рамок урока («могу»): пересечение множеств.
3) организовать актуализацию требований к ученику со стороны учебной деятельности («надо»).
Организация учебного процесса на этапе 1:
1)- Ребята к нам сегодня пришли гости. Давайте поздороваемся.
– Вы любите тайны? (Да)
Сегодня на уроке мы с вами будем раскрывать математические тайны.
Давайте подумаем каким образом вы будите это делать? (С повторения того, что нам пригодится для открытия нового.)
— Пожелайте друг другу удачи и поднимаясь по нашей математической лестнице вы сможете узнать новую тайну.

Организация учебного процесса на этапе 2:
К нам в гости на урок пришла буква Я, которая вместе с нами будет раскрывать математические тайны.(На доску вывешивается буква Я).
Предлагаю вам до повторения необходимого потренироваться в устном счёте. (Под первой ступенькой появляется слово повторение).
Кто сегодня подготовил математический диктант? Кто? (Сафронова А.)
33 больше задуманного числа на 8. Какое число задумано?
Задуманное число меньше 42 на 10. Какое число задумано?
Какое число надо прибавить к 17, чтобы получить 56?
Какое число надо вычесть из 61, чтобы получить 15?
70 больше неизвестного числа на 17. Чему равно неизвестное число?
44 меньше неизвестного числа на 16. Чему равно неизвестное число?
– Проверим. (25; 32; 39; 46; 53, 60; ).
– Посмотрите закономерность и скажите следующие три числа в данном ряду чисел. (Числа увеличиваются на 7. Следующее число 67;74; 81.)
(Числа увеличиваются на 7. Следующее число 67;74; 81.)
О В Т С Е Ж О Н М
— Какое слово получилось?
— Раскрываем следующую тайну.
В
Перечислите элементы множества А и множества В.
Что значит «общие элементы» множеств? (В множестве А есть такие же элементы, как и в множестве В.)
Где находится точка 2? (На пересечении этих двух множеств.)
Что называют «пересечением» множеств? (Правило). На доске появляется стебель (цветка) со словом ПЕРЕСЕЧЕНИЕ).
На слайде — математические выражения:
(5 48) 2
2) Актуализация представлений о переместительном и сочетательном свойствах сложения и умножения.
Назовите эту запись математическим термином. (Выражение.)
Какие свойства операций умножения вы знаете? (Переместительное, сочетательное и распределительное.
 )
)Для чего используют эти свойства? (Для удобства вычислений.)
Найдите значение этого выражения, пользуясь свойствами. Каким свойством вы воспользуетесь? (Сочетательным. От изменения порядка действий произведение не изменяется.) Назовите сочетательное свойство.
Учитель вывешивает эталон с лепестком:
(a · b) · c = a · (b · c)
-Примените сочетательное свойство умножения при решении этого выражения.
(Дети делают самостоятельно)
— Скажите, какие множители вы сгруппировали.(5и2)
— Проверьте свою запись.(Слайд)
(5 · 48) · 2 = (5 · 2) · 48 = 10 · 48 = 480.
— Каким свойством мы сейчас пользовались?(Сочетательным)
— А если знак умножения заменить на знак плюс, что мы получим?
(Сочетательное свойство сложения)
— Давайте хором его назовём. ((a + b) + c = a + (b + c)
((a + b) + c = a + (b + c)
(Вывешиваю лепесток на доску)
— Какие свойства мы повторили?(сочетательное свойство умножения и сочетательное свойство сложения)(Слайд)
— На проекторе новое выражение(СЛАЙД)
259 + 648…648 + 259
Посмотрите на следующее выражение. Какой знак надо поставить между выражениями?(=)
— Почему?(Они равны)
a + b = b + a (вывешиваю свойство)
Какое ещё переместительное свойство вы знаете?(Переместительное свойство умножения)
— Назовите его.( a · b = b · a )
(Вывешиваю на доску лепесток)
Давайте назовём, что мы с вами сейчас повторили? ( Показываю на цветке и повторяю с детьми (Множество, пересечение, переместительное и сочетательные свойства умножения и сложения, сравнивали выражения).
Давайте произнесём какие главные слова были у нас на этом этапе повторения? (Множество, пересечение, свойство)
Кто может используя эти слова сформулировать тему нашего урока? («Свойства пересечения множеств».
 )
)
(Учитель вывешивает кружок в середину цветка с названием темы на доску и буква Я переходит на лестницу НОВОЕ).
Значит, какую цель поставим перед собой? (Выяснить, обладает ли пересечение множеств переместительным и сочетательным свойствами, записать и сформулировать его.)
3. Выявление места и причины затруднения.
Цель:
1) организовать восстановление выполненных операций и фиксацию (вербальную и знаковую) места – шага, операции, где возникло затруднение;
2) организовать соотнесение действий учащихся с используемым способом (алгоритмом, понятием и т.д.) и на этой основе организовать выявление и фиксирование во внешней речи причины затруднения – тех конкретных знаний, умений или способностей, которых недостаёт для решения исходной задачи такого класса или типа.
На проекторе появляется.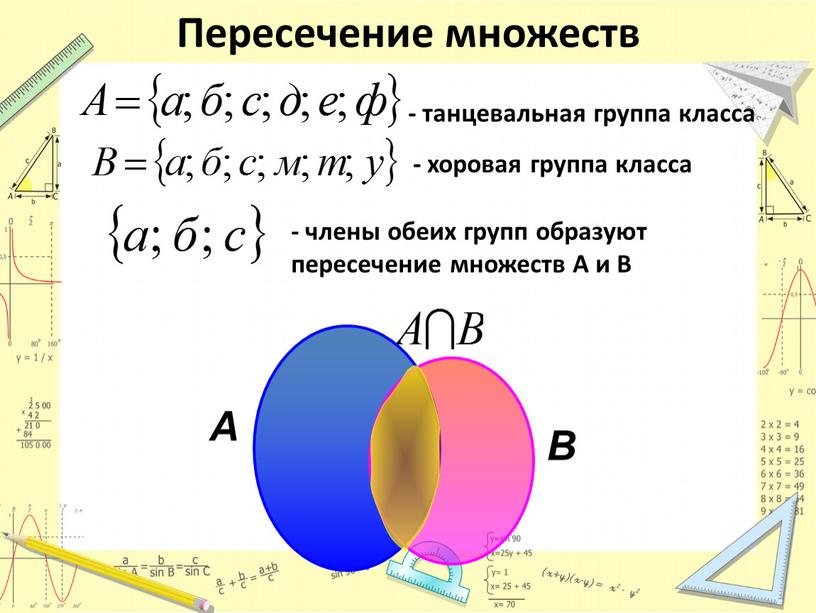 (CЛАЙД)
(CЛАЙД)
А ∩ В … В ∩ А
(А ∩ В) ∩ С …..А ∩ (В ∩С)
— Что нового в этом задании? (Надо определить, верны равенства с пересечениями или нет, а мы такого никогда не делали).
— Попробуйте выполнить задание на маркерных досках.
— Проверим выполнение. Кто не справился с заданием? Почему возникла у вас проблема? (Мы не можем определить, равны эти пересечения или нет.)
— Кто определил, верны или нет эти равенства?
Какое задание вы выполняли? (Мы должны были определить, верно ли то, что пересечения множеств равны.)
Как вы выполняли задания? (…)
Где у вас возникло проблема?
Почему она возникло? (У нас нет правила, эталона, чтобы определить, верны ли эти равенства.)
— Давайте вернёмся к числовым выражениям.
Что помогло нам сравнить числовые выражения? (Свойства сложения и умножения. )
)
Посмотрите на эталоны, которые висят на доске. На какие из них похожи данные равенства? (Первая – на переместительное свойство умножения и сложения, вторая – на сочетательное…)
А, может быть, данными свойствами обладают и пересечения множеств? И именно эти знания помогут нам.
— Вспомните ещё раз, что мы повторяли. Подумайте, что поможет вам доказать, что пересечения множеств обладают свойствами сочетательным и переместительным.
Проверим, обладает операция пересечения множеств переместительным и сочетательным свойствами или нет. Сейчас мы будем работать в группе. Не забывайте как надо работать в группе.
— Умеем мы задавать множества? Умеем обозначать их на диаграммах?
Проверим, обладает операция пересечения множеств переместительным и сочетательным свойствами или нет.
Форма работы: групповая на планшетах.
— Перед вами задание №1. Прочитайте внимательно задание и выполните его на маркерных досках.
1. Задайте множества А и В пересечением.
— Изобразите с помощью диаграммы Венна множество А, множество В. Что заметили? Сделайте вывод. (Они имеют общие элементы, их пересечение равно…)
Изобразим множество В, множество А. Что заметили?
Сделайте вывод. (Получился такой же результат.)
Какой вывод вы можете сделать? (Пересечение множеств обладает переместительным свойством.)
— 2. Задайте множества А , В и С пересечением.
— Изобразите с помощью диаграммы Венна множество А, множество В и множество С. Что заметили? (Они имеют общие элементы, их пересечение равно…)
— Какой вывод можете сделать? (Пересечение множеств обладает сочетательным свойством).
— Где можем проверить наш вывод? (В учебнике.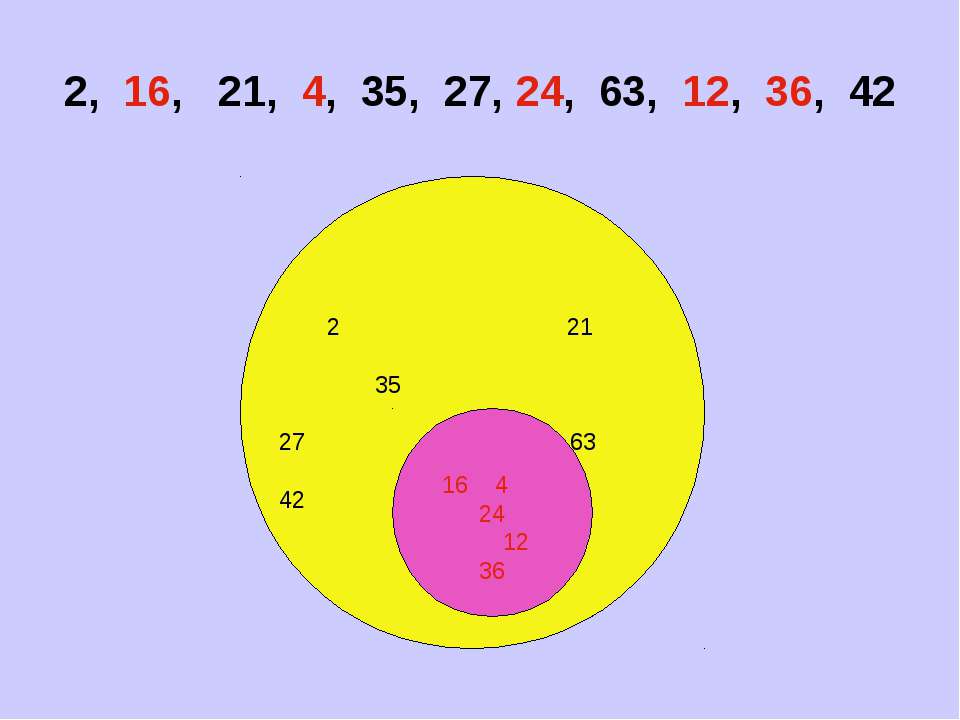 )
)
Обращаются к учебнику стр. 27, проверяют себя.
— Что мы доказали? (Что пересечение множеств обладает переместительным и сочетательным свойствами, а стало быть, предложенные нам равенства верны.)
Справились с проблемой? (Да.)
Молодцы! Вы открыли ещё одну математическую тайну. Учитель вывешивает на доску два лепестка со свойствами пересечения множеств.
4.ФИЗКУЛЬТМИНУТКА
5. Первичное закрепление.
Цель:
1) На проекторе появилось выражение: (СЛАЙД)
«НОВОЕ УМЕНИЕ ВЕЗДЕ НАЙДЁТ ПРИМЕНЕНИЕ».
Как вы думаете, чем займёмся? (Будем применять новое умение в заданиях.)
Н
Задание:
А = {1; 2; 3; 4}, В = {3; 4; 5}. Запиши с помощью фигурных скобок множества
А ∩ В и В ∩ А. Отметь элементы этих множеств на диаграмме Венна.
ачнём с № 2 стр. 27. Прочитайте задание.(Работает у доски Шнурков Даниил), остальные учащиеся работают в учебнике) Сделай вывод.
Сделай вывод.
Перечислите элементы множества А. (А = {1; 2; 3; 4}.)
Перечислите элементы множества В. (В = {3; 4; 5}.)
Какие элементы являются общей частью множеств А и В, В и А? (Элементы 3 и 4.)
Запишите элементы множеств А и В и отметьте их на диаграмме. (А ∩ В = {3; 4},
В ∩ А = {3;4}.)
Докажите. (Пересечение множеств не зависит от порядка множеств.)
2) № 3, стр. 27
Прочитайте задание. (Работает у доски Курашов Андрей, остальные учащиеся работают в учебнике)
Чем отличаются записи (А ∩ В) ∩ С = А ∩ (В ∩ С)? (В первом случае сначала находится пересечение множеств А и В, затем его пересечение с множеством С. Во втором случае, наоборот, сначала находится В ∩ С, а затем его пересечение с А.
 )
)
— Какой вы сделайте вывод. (Пересечение множеств не зависит от порядка действий.)
6.Работа в парах с самопроверкой по эталону.
Цель:
1) организовать самостоятельное выполнение учащимися заданий на новые понятия;
2) организовать самооценку детьми правильность выполнения задания (при необходимости – коррекцию возможных ошибок).
На проекторе выражением: « ТОРОПИСЬ — ДА НЕ ОШИБИСЬ!»(СЛАЙД)
Как вы думаете, к какому виду деятельности подходит это выражение? (самостоятельная работа).
С какой целью мы выполняем эту работу? (Чтобы выяснить, как усвоили новые знания.)
— Перед вами задание №2.
Прочитайте внимательно задание и выполните его на листочках.
Задание:
Допишите равенства, выражающие переместительное и сочетательное свойства операции пересечения множеств:
М ∩ К =
(М ∩ К) ∩ Т =
(Слад)
М ∩ К = К ∩ М Пересечение множеств не зависит
от порядка множеств и порядка
(М ∩ К) ∩ Т = М ∩ (К ∩ Т) действий.
Проверка:
Поставьте знак «+», если вы выполнили так же «?» если по-другому.
Какие были затруднения? (…)
Исправьте ошибки.
7. Физкультминутка для глаз и дыхания .
8.Включение в систему знаний и повторение.
Цель:
1) тренировать вычислительные навыки через решение примеров с использованием свойств для сложения и умножения;
2) повторить решение задач на приведение к единице, составление и решение уравнений, порядок действий в выражениях со скобками;
3) проверить у детей способность к оценке собственных достижений.
Организация учебного процесса на этапе 8:
— Новые знания помогут нам в дальнейшем при решении задач, но мы с ними встретимся на других уроках.
На проекторе выражение: «ПОВТОРЕНИЕ — МАТЬ УЧЕНИЯ».(СЛАЙД)
Прочитайте выражение и подумайте, чем мы продолжим заниматься? (Повторим те знания, которые изучили раньше.
 )
)
Форма работы: индивидуальная.
Решение задания по выбору.
Учащиеся, по желанию выбирают одно из заданий № 7(а), 9(а), 11(а) стр. 28.
Перед выбором учитель даёт установку к заданиям.
Если вы выберите № 7(а) стр. 28, то проверите своё умение решать задачи.
Если у вас трудности в решении уравнений, полезно будет выполнить № 9(а) стр. 28.
Выполнение № 11(а) стр. 28 повысит ваши вычислительные навыки.
Но вы можете выбрать и то задание, которое вам больше понравилось.
На слайде учитель фиксирует:
№ 7 (а) стр. 28 – задача;
№ 9 (а) стр. 28 – уравнение;
№ 11 стр. 28 – вычисления.
После выполнения заданий самопроверка по образцам который лежит у учителя на столе.
№7(а)
4 под. – n кв.
6 под. — ? кв.
1 под. — ? кв.
Ответ: 96 квартир в 6 подъездах.
№
9(а)а) х – 394 = 286; 286
х = 286 + 394; 394
х = 670 670
286 + 394 = 670
670 = 670
№11(а)
а) (13 + 8 · 4 ) : 5 – (27 : 3 – 0 · 6) = 9 – 9 = 0
0
45 9
1) № 6 стр. 28.
Ученик с места читает задание.
На слайде алгоритм рассуждений для вычислений.
Читаю выражение
Определяю свойство, которое можно использовать для упрощения вычислений
Вычисляю
Образец рассуждения:
Читаю выражение: (298 + 386) + 102.
Определяю свойство: переместительное и сочетательное свойства сложения.
Вычисляю: (298 + 386) + 102 = (386 + 298) + 102 = 386 + (298 + 102) = 386 + 400 = 786.

Какая ещё операция обладает переместительным и сочетательным свойствами? (Операции умножения, пересечения множеств.)
– Молодцы! Как считаете раскрыли вы сегодня на уроке новую математическую тайну?(Да)
10. Рефлексия учебной деятельности на уроке.
Цель:
1) зафиксировать новое содержание, изученное на уроке;
2) организовать рефлексивный анализ учебной деятельности с точки зрения выполнения требований, известных учащимся;
3) оценить собственную деятельность;
4)зафиксировать неразрешенные на уроке затруднения, если они есть, как направления будущей учебной деятельности;
5) обсудить домашнее задание.
Организация учебного процесса на этапе 11:
— Что нового узнали на уроке? (Операция пересечения множеств обладает переместительным и сочетательным свойствами.)
— Какую цель вы поставили сегодня на уроке? (Выяснить, обладает ли пересечение множеств переместительным и сочетательным свойствами, записать и сформулировать его. )
)
Справились вы с поставленной целью?(Да)
Что нам доказывает?
Ребята у которых возникла проблема в выполнение самостоятельной работы, ещё раз дома её сделайте.
— Наша буква Я переходит к следующим словам.
— Я УЗНАЛ?
-Я НАУЧИЛСЯ?
— Я ЗАПОМНИЛ?
— Я УВИДИЛ?
Первая ступенька — многое не понял и остались вопросы; вторая ступенька — многое понял, но были ошибки; третья ступенька — трудности преодолены.
Домашнее задание:
№ 5 стр. 28, № 8 стр. 28;
I. Актуализация знаний. | 1. Организационный момент. Учитель поднимает руку и говорит, обращаясь к классу: «Хай файв!» Учащиеся в ответ должны тоже поднять руку и посмотреть на учителя. Слайд 1. Нету солнышко с утра, Вы пришли сюда учиться, – Я рада, что у Вас хорошее настроение. Поприветствуйте друг друга: партнеры по плечу дайте пять друг другу. У вас есть листочки в клеточку. Прошу подписать их в верхнем правом углу. Так же запишите число и классная работа. Слайд2. Выполните и сравните свой ответ с партнёром по плечу. Какое слово у вас получилось? (Множество) Давайте проверим. Слайд 3. Поставьте + на полях. – Что такое множество? Слайд 4. Это тема, над которой мы работаем уже несколько уроков. – Можно ли назвать предметы, на данном рисунке, множеством? (Да, это группа живых существ собранных вместе.) – Назовите это множество. (Множество бабочек.) Слайд 5,6,7.(Насекомые) Структура МИКС ПЭА ШЭА – структура, в которой участники смешиваются под музыку, образовывают пару, когда музыка прекращается, обсуждают предложенную тему, используя структуру РЕЛЛИ РОБИН (для коротких ответов) «Назовите множество». 1.Множество лошадей -… (табун) 2. Множество коров -… (стадо) 3. Множество овец — … (отара) 4. Множество рыб — … (косяк) 5. 6. Множество собак — … (свора) 7. Множество птиц — … (стая) 8. Множество пчел — … (рой) 9. Множество дубов- … (дубрава) 10. Множество берёз — … (роща) 11 Множество сосен- … (бор) 12 Множество елей — … (ельник) О-О-Отлично!!! Слайд 8. – Из чего состоят множества? (Множества состоят из элементов) Что такое элементы множества? ( Элементы множества – это предметы, объекты или живые существа, из которых состоит множество.) – Что можно сделать с элементами множества? (Посчитать и перечислить их.) Слайд 9. – Посчитайте и перечислите элементы множества «Овощи». Слайд 10. Обсудите с партнёром по плечу и назовите элементы множества: “Месяцы года” -1стол “Времена года” -2стол “Материки” -3стол Евразия, Африка, Южная Америка, Северная Америка, Антарктида и Австралия. “Летающие бегемоты” -4стол «Дни недели» — 5 стол А сейчас партнёры 1 стола расскажут партнёрам 2 стола, 3-4, 5- мне. Послушать 3 и 4 стол. Если вы правильно назвали все элементы своих множеств то поставьте +… | Познавательные УУД Развиваем умения: 1 ориентироваться в своей системе знаний: самостоятельно предполагать, какая информация нужна для решения учебной задачи в один шаг. | II. Сообщение нового знания (узнаём…). | Слайд 11.– Перед вами два множества. Посмотрите внимательно на элементы. – Дайте названия данным множествам по цвету и материалу изготовления. (Множество зелёных объектов и множество деревянных объектов) – Давайте распределим данные объекты по множествам. Проверьте, всё ли мы верно сделали? Слайд 12.– Что вы заметили? (Что некоторые объекты, карандаш и кубик подходят и в первое и во второе множество.) – По свойствам эти предметы подходят И к множеству деревянных предметов И к множеству зелёных предметов. Они являются общими для этих двух множеств. – Посмотрите, как это можно показать по другому Слайд 13.– Эти элементы являются общими и для первого и для второго множества. – Поэтому они находятся в пересечении множеств. – Попробуйте дать общее название элементам находящимся в пересечении. Слайд 14. Вывод. – Так какую часть множеств называют пересечением? (Общую часть множеств называют пересечением.) Если в названии множества есть слово «И», то каждый его элемент должен находиться на ПЕРЕСЕЧЕНИИ двух множеств. Слайд 15. Кто уже догадался и может назвать тему урока. (Пересечение множеств) Открыть на доске. .Давайте поставим цель работы. (Сформировать представление о понятии «пересечение» множеств.) Слайд 16.Какие задачи урока нужно выполнить? узнать какую часть множеств называют «пересечением»; узнать какие элементы множеств входят в область пересечения; научиться изображать пересечение множеств при помощи графической модели Работа с учебником. Слайд 17. 1. Задание № 1, с. Цель работы: – актуализация знаний о пересечении геометрических фигур; – создание (через совместный анализ рисунков и текста) представления о пересечении геометрических фигур как наличии общей части (множества точек). Витя начертил фигуры и раскрасил их синим и жёлтым цветом. Какая фигура является общей частью прямоугольника и треугольника? (четырёхугольник) — Какого цвета фигура получилась? Почему? — Чем является зелёный четырёхугольник для этих фигур? (Пересечением) 2. Задание № 2, с. 50 Цель работы: – отталкиваясь от понимания того, что зелёным цветом обозначена общая часть жёлтого и синего множеств (множества шаров и множества красных фигур), прийти к пониманию того, что, наверное, красный шар – это общий элемент двух множеств; – объяснить, почему красный шар принадлежит обоим множествам. Слайд 18.Лика нарисовала внутри этих фигур элементы множеств. — Обсудите задание с партнёром по плечу и подготовьте ответы на вопросы. — Почему красный шар принадлежит обоим множествам? — Как можно назвать теперь красный шар, который принадлежит двум множествам? (Элемент пересечения множеств). | 1. — отбирать необходимые для решения учебной задачи источники информации среди предложенных учителем словарей, энциклопедий, справочников. 2 — добывать новые знания: извлекать информацию, представленную в разных формах (текст, таблица, схема, иллюстрация и др.). 3 — перерабатывать полученную информацию: сравнивать и группировать математические факты и объекты. 4 — делать выводы на основе обобщения умозаключений. 5 — преобразовывать информацию из одной формы в другую: — представлять информацию в виде текста, таблицы, схемы. 6 – переходить от условно-схематических моделей к тексту. | III. Первичное закрепление (применяем…). | Слайд 19. 1. Задание № 3, с. 50 Заполните графическую модель элементами с областью пересечения. 5 элементов добавьте в область двузначных чисел и нечётных. У вас на столах есть бумага и фломастеры. Проверка. Кто сделал задание верно поставьте + на полях. Слайд 20. б). В нашей школе есть третьеклассники, а ещё в школе есть много девочек. девочки — третьеклассницы Приведите примеры. Так это кто? Это могут быть девочки из нашего класса? (имена девочек класса). Слайд 21. 2. Задача № 4, с. 50 — Прочитайте самостоятельно задачу. — Прочитайте условие задачи. — Прочитайте вопрос. -Что известно в задаче? Что нужно найти? Слайд 22. — Рассмотрите графическую модель задачи. — Назовите элементы первого множества. — Назовите элементы второго множества. — Назовите элементы пересечения этих множеств. — Известно ли это количество? — Для решения давайте используем счётный материал. — Выложите на парты указанное в условии количество элементов каждого множества, в одну линейку. а) На столах у детей лежит по 14 белых кружков (третьеклассники) и по 7, красных кружков (девочки). -Скажите, что можем узнать по этим данным? Слайд 23. (Если бы одна часть гостей была бы только третьеклассниками, а другая часть только девочками, то было бы 14 + 7 гостей). б) — Какое ещё условие необходимо учитывать? (Среди них есть девочки-третьеклассницы. — Прокомментируйте, как это можно определить? Слайд 24. (Часть гостей являются одновременно и девочками, и третьеклассниками, поэтому гостей не 21, а 15. Разность между этими числами и есть число девочек-третьеклассниц). Поднимите руку кто понял, как решать задачу. Решайте. Поднимите руку кто сомневается. А теперь поднимите руку, кто совсем ничего не понял. Ученицы 2 стола решат задачу на доске. А остальные решают на листочках в клеточку. Проверка. (Прослушать одного ученика, показать готовое решение на слайде) Кто решил задачу верно поставьте + на полях Слайд 25. в) Решение: 14 + 7 – 15 = 6 девочек-третьеклассниц. Кто решил задачу верно поставьте + на полях О-О-Отлично!!! Прошу всех встать. Нашим девочкам третьеклассницам я дарю розочку. Физминутка. Самостоятельная работа. 3. Придумайте и решите похожую задачу с. 51. Слайд 27. — О каких множествах эта задача? — Что является пересечением этих множеств? — Какие данные вы видите на рисунке? — Кто может рассказать план решения задачи. (Сначала найти общее количество элементов множеств хищников и птиц, потом вычесть общее количество животных: (учащиеся решают задачу на специальных досках) (4 стол) Одна пара выполняет решение задачи на доске. Слайд 28. 48 + 49 – 87 = 10 (хищных птиц). Проверка на слайде по алгоритму самооценки. Вопросы к ученикам, выполнявшим работу: – Что вам нужно было сделать в задании? – Удалось ли правильно решить поставленные задачи? – Вы сделали всё правильно или были ошибки, недочёты? – Вы решили всё сами или с чьей-то помощью? — Оцените свою работу. — Есть ли у ребят какие-либо дополнения, замечания? Согласны ли вы с такой самооценкой? Кто решил так же задачу поставьте +. Молодцы, задачу вы решили. А сейчас я вам предлагаю в течении 5 минут поработать с текстом. Изучить материал про хищных птиц и представить его своим одноклассницам. Заслушиваются 3 выступления монологического ответа про хищных птиц. | Регулятивные УУД: Развиваем умения: 1 – самостоятельно формули-ровать цели урока после предварительного обсуждения; 2 – совместно с учителем обнаруживать и формулировать учебную проблему; 3 – составлять план решения отдельной учебной задачи совместно с классом; 4 – работая по плану, сверять свои действия с целью и, при необходимости, исправлять ошибки с помощью класса; 5 – в диалоге с учителем и другими учащимися учиться вырабатывать критерии оценки и определять степень успешности выполнения своей работы и работы всех, исходя из имеющихся критериев. Коммуникативные УУД Развиваем умения: 1 — доносить свою позицию до других: оформлять свои мысли в устной и письменной речи (выражение решения учебной задачи в общепринятых формах) с учётом своих учебных речевых ситуаций; 2 – доносить свою позицию до других: высказывать свою точку зрения и пытаться её обосновать, приводя аргументы; 3 – слушать других, пытаться принимать другую точку зре-ния, быть готовым изменить свою точку зрения; 4 – читать про себя тексты учебников и при этом: ставить вопросы к тексту и искать ответы; проверять себя; отделять новое от известного; выделять главное; составлять план; ТОУУ 5 – договариваться с людьми: выполняя различные роли в группе, сотрудничать в совместном решении проблемы (задачи). ТОУУ Личностные результаты: 1 – придерживаться этических норм общения и сотрудничества при совместной работе над учебной задачей; 2. | IV.Задания на повторение. Тренинг (выбираем…). | Слайд 29. Задание № 6, с. 51 Витя записал названия множеств и составил высказывания. Нарисуйте эти множества в виде графической модели и впишите в них названия. А) Все апельсины-фрукты. Не все фрукты-апельсины. Проверка. Где здесь область пересечения множеств? Б) Никакие кролики- не зайцы. Никакие зайцы- не кролики. Проверка. Где здесь область пересечения множеств? О-о-отлично! Задача № 7, с. Основные цели: 1. Подготовить детей к знакомству с уравнениями нового вида, которые будут вводиться через текстовую задачу. 2. Учиться выделять (путём наблюдения) в тексте задачи величину, которая будет приниматься за основное неизвестное (х). 3. Учиться выражать через основное неизвестное (х) остальные величины (составлять уравнение). Структура СИМАЛТИНИУС РЕЛЛИ ТЭЙБЛ – «одновременный раунд тейбл» — структура, в которой 2 участника в паре одновременно выполняют письменную работу в тетради и по окончанию времени передают работу друг другу, для проверки.
— Решите уравнения. Стол №5 партнёр 1 озвучит корни уравнений. (1 =110, 2 =75, 3 =3, 4 =80) Проверка, оценивание. Кто выполнил так же уравнение поставьте +. Задача. В корзине лежало несколько фруктов, когда из неё достали 90 апельсинов, то в ней осталось ещё 20 фруктов. Сколько фруктов лежало в корзине первоначально? — Обсудите с партнёром, какое уравнение составлено к данной задаче? — Как рассуждали? — Какая неизвестная величина в уравнении обозначена х? — Как по условию задачи составлено уравнение? -Какой вывод можно сделать? (Задачи можно решать при помощи уравнения) |
Объединение и пересечение множеств — математика, уроки
Изучение нового материала.
Стратегия «Инсерт». Групповая работа.
Каждая группа выбирает для изучения одну из тем : «Пересечение множеств», «Объединение множеств».
Учащиеся в группе читают текст учебника стр. 102-103, делая пометки:
102-103, делая пометки:
«v» -известная информация;
«+» — новая информация;
«?» — непонятная информация;
« » — информация, идущая вразрез с имеющимися представлениями и знаниями.
После работы с текстом – обсуждение с обязательным обращением к исходному тексту, цитированием.
Оценивание. Цитата. Комментарий к цитате.
Дескрипторы
формулируют определение объединения множеств;
формулируют определение пересечения множеств;
выделяют множества и подмножества.
Стратегия «Динамическое упражнение». Работа в группах.
Учащиеся обсуждают решение в группе, каждый участник группы записывает его в тетрадь.
Все группы решают №1054 и представляют на доске:
группа А пункт а) А={4,20,5,10,2,1},
группа В пункт б) B={1,2,5,10,50,25},
группа С пункт в) А∩В={1,2,5,10},
группа D пункт г)AUB={4,20,1,2,5,10,25,50}.
Самопроверка. Проводят проверку правильности выполнения по готовому образцу
Дескрипторы
Обучающиеся:
— записывают множества перечислением;
— используют в записи символы ∩, U.
Дифференциация. Стратегия «Кубик». Индивидуальная работа.
На гранях кубика дается задание. Три грани – задания уровня А, две грани задания уровня В, одна грань задание уровня С. Выбрасывается кубик, в группе учащиеся сами выбирают, кто будет решать задание какого уровня. Задание выполняется на листахА4. Если учащиеся быстро справляются с заданиями, они еще раз по очереди бросают кубик.
Задания:
Группа А — №1052, № 1053, № 1055
Группа В — № 1057, №1060.
Группа С — № 1072
Выполняется взаимопроверка в группах.
Оценивание. Стратегия «Две звезды, одно пожелание»
Дескрипторы
— изображают кругами Эйлера-Венна соотношение между множествами;
— используют символы ∩, U
— решают задачу используя круги Эйлера-Венна;
— выбирают объект по рисунку;
— составляют задачу и решают ее.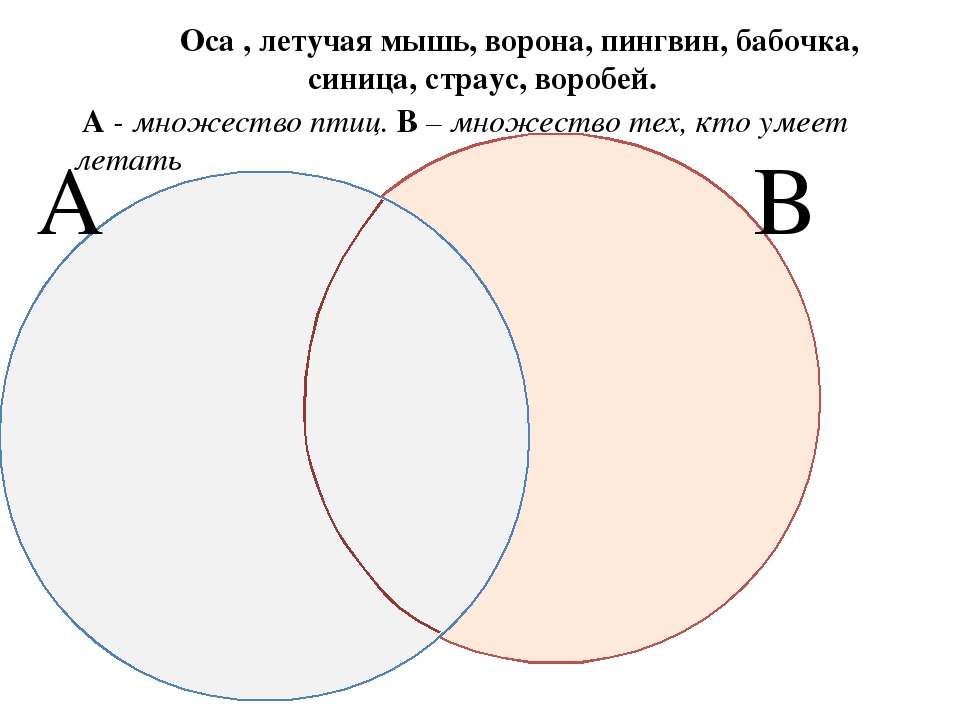
Урок 9. Пересечение множеств. Знак ∩
Урок 9. Пересечение множеств. Знак ∩ — Ответы и ГДЗ к учебнику по математике 3 класс 1, 2, 3 часть (Петерсон) 1. а) Обведи желтым карандашом замкнутую линию А, а синим карандашом — замкнутую линию В. Отметь красным карандашом точки, в которых эти линии пересекаются.б) Области внутри линий А и В раскрась соответственно желтыми и синим цветом. Какую часть этих областей пришлось закрасить дважды? Обведи ее границу красным. Это — общая часть двух областей.
2. К — множество детей, которые были на дне рождения у Коли, Т — множество детей, которые были на дне рождении у Тани. Построй диаграммы этих множеств, если К={Шура, Надя, Петя}, Т={Надя, Петя, Миша, Лена}.
Найди общие элементы этих множеств. Обозначь на диаграмме пересечение множеств цветным карандашом.
3.
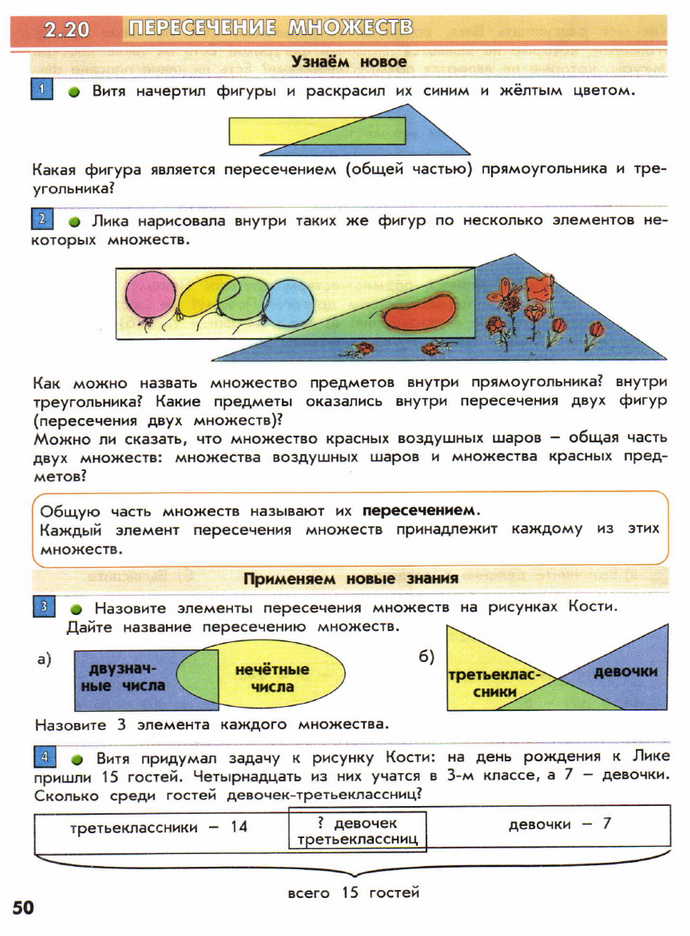 А — множество учеников, изучающих английский язык, F — множество учеников, изучающих французский язык. Что представляет собой множество А∩F?
А — множество учеников, изучающих английский язык, F — множество учеников, изучающих французский язык. Что представляет собой множество А∩F?4. Определи по рисункам, каким свойством обладают элементы пересечения множеств А и В. Обведи общую часть диаграммы этих множеств цветным карандашом.
5. Даны множества М и К. Запиши с помощью фигурных скобок множество М∩К. Отметь элементы множеств М и К на диаграмме Эйлера-Венна и обведи цветным карандашом множество М∩К.
6. На каждом рисунке закрась цветным карандашом множество А∩В.
7. Множества А и В на рисунке не имеют общих элементов. Такие множества называются непересекающимися. Приведи свои примеры непересекающихся множеств и допиши равенство.
8. Начерти два треугольника так, чтобы их пересечением были: а) шестиугольник; б) пятиугольник; в) четырехугольник; г) треугольник; д) отрезок; е) точка; ж) пустое множество.

9. БЛИЦтурнир.
а) Оля испекла а пирожков, а ее сестра — b пирожков. Эти пирожки они разложили поровну на 3 тарелки. Сколько пирожков в каждой тарелке?
б) В 7 одинаковых банках d литров сока. Сколько сока в 20 таких банках?
в) С первой грядки собрали с огурцов, а со второй — на b огурцов меньше. Во сколько раз больше огурцов собрано с первой грядки, чем со второй?
г) В коробке было n конфет. Четверо ребят взяли по а конфет. Сколько конфет осталось в коробке?
д) В вазе лежало а груш, яблок в 3 раза больше, чем груш, а апельсинов на b меньше, чем яблок. Сколько всего груш, яблок и апельсинов лежало в вазе?
10. Найди значения выражений.
11. Подбери корни уравнения.
12.
 От Бабы-Яги до Кощея ведут 3 дороги, а от Кощея до Кикиморы — 4 дороги. Сколькими способами можно дойти от Бабы-Яги до Кикиморы по этим дорогам?
От Бабы-Яги до Кощея ведут 3 дороги, а от Кощея до Кикиморы — 4 дороги. Сколькими способами можно дойти от Бабы-Яги до Кикиморы по этим дорогам?
Набор Python (с примерами)
Набор — это неупорядоченный набор предметов. Каждый элемент набора уникален (без дубликатов) и должен быть неизменным (не может быть изменен).
Однако сам набор изменчив. Мы можем добавлять или удалять элементы из него.
Наборы также могут использоваться для выполнения математических операций над наборами, таких как объединение, пересечение, симметричная разность и т. Д.
Создание наборов Python
Набор создается путем помещения всех элементов (элементов) в фигурные скобки {} , разделенных запятыми, или с помощью встроенной функции set () .
Он может иметь любое количество элементов, и они могут быть разных типов (целые числа, числа с плавающей запятой, кортеж, строка и т. Д.). Но набор не может иметь в качестве своих элементов изменяемые элементы, такие как списки, наборы или словари.
Д.). Но набор не может иметь в качестве своих элементов изменяемые элементы, такие как списки, наборы или словари.
# Различные типы наборов в Python
# набор целых чисел
my_set = {1, 2, 3}
печать (my_set)
# набор смешанных типов данных
my_set = {1.0, "Привет", (1, 2, 3)}
печать (my_set) Выход
{1, 2, 3}
{1.0, (1, 2, 3), «Привет»} Попробуйте также следующие примеры.
# set не может иметь дубликатов
# Вывод: {1, 2, 3, 4}
my_set = {1, 2, 3, 4, 3, 2}
печать (my_set)
# мы можем сделать набор из списка
# Вывод: {1, 2, 3}
my_set = set ([1, 2, 3, 2])
печать (my_set)
# набор не может иметь изменяемые элементы
# здесь [3, 4] - изменяемый список
# это вызовет ошибку.
my_set = {1, 2, [3, 4]} Выход
{1, 2, 3, 4}
{1, 2, 3}
Отслеживание (последний вызов последний):
Файл «<строка>», строка 15, в <модуле>
my_set = {1, 2, [3, 4]}
TypeError: нехешируемый тип: 'list' Создать пустой набор немного сложно.
Пустые фигурные скобки {} создадут пустой словарь в Python. Чтобы сделать набор без каких-либо элементов, мы используем функцию set () без аргументов.
# Различать набор и словарь при создании пустого набора
# инициализировать a с помощью {}
а = {}
# проверить тип данных
печать (тип (а))
# инициализировать a с помощью set ()
а = набор ()
# проверить тип данных
печать (тип (а)) Выход
<класс 'dict'> <набор классов>
Изменение набора в Python
Наборы изменяемы.Однако, поскольку они неупорядочены, индексация не имеет значения.
Мы не можем получить доступ к элементу набора или изменить его с помощью индексации или нарезки. Установить тип данных не поддерживает его.
Мы можем добавить один элемент с помощью метода add () и несколько элементов с помощью метода update () . Метод update () может принимать в качестве аргумента кортежи, списки, строки или другие наборы. Во всех случаях следует избегать дублирования.
Во всех случаях следует избегать дублирования.
# инициализировать my_set
my_set = {1, 3}
печать (my_set)
# если вы раскомментируете строку 9,
# вы получите сообщение об ошибке
# TypeError: объект 'set' не поддерживает индексацию
# my_set [0]
# добавить элемент
# Вывод: {1, 2, 3}
my_set.добавить (2)
печать (my_set)
# добавить несколько элементов
# Вывод: {1, 2, 3, 4}
my_set.update ([2, 3, 4])
печать (my_set)
# добавить список и установить
# Вывод: {1, 2, 3, 4, 5, 6, 8}
my_set.update ([4, 5], {1, 6, 8})
печать (my_set) Выход
{1, 3}
{1, 2, 3}
{1, 2, 3, 4}
{1, 2, 3, 4, 5, 6, 8} Снятие элементов из набора
Определенный элемент можно удалить из набора с помощью методов discard () и remove () .
Единственное различие между ними состоит в том, что функция discard () оставляет набор неизменным, если элемент отсутствует в наборе. С другой стороны, функция
С другой стороны, функция remove () вызовет ошибку в таком состоянии (если элемент отсутствует в наборе).
Это проиллюстрировано на следующем примере.
# Разница между discard () и remove ()
# инициализировать my_set
my_set = {1, 3, 4, 5, 6}
печать (my_set)
# отбросить элемент
# Вывод: {1, 3, 5, 6}
my_set.выбросить (4)
печать (my_set)
# удалить элемент
# Вывод: {1, 3, 5}
my_set.remove (6)
печать (my_set)
# отбросить элемент
# отсутствует в my_set
# Вывод: {1, 3, 5}
my_set.discard (2)
печать (my_set)
# удалить элемент
# отсутствует в my_set
# вы получите сообщение об ошибке.
# Вывод: KeyError
my_set.remove (2) Выход
{1, 3, 4, 5, 6}
{1, 3, 5, 6}
{1, 3, 5}
{1, 3, 5}
Отслеживание (последний вызов последний):
Файл «<строка>», строка 28, в <модуле>
KeyError: 2 Точно так же мы можем удалить и вернуть элемент, используя метод pop () .
Поскольку set — это неупорядоченный тип данных, невозможно определить, какой элемент будет выталкиваться.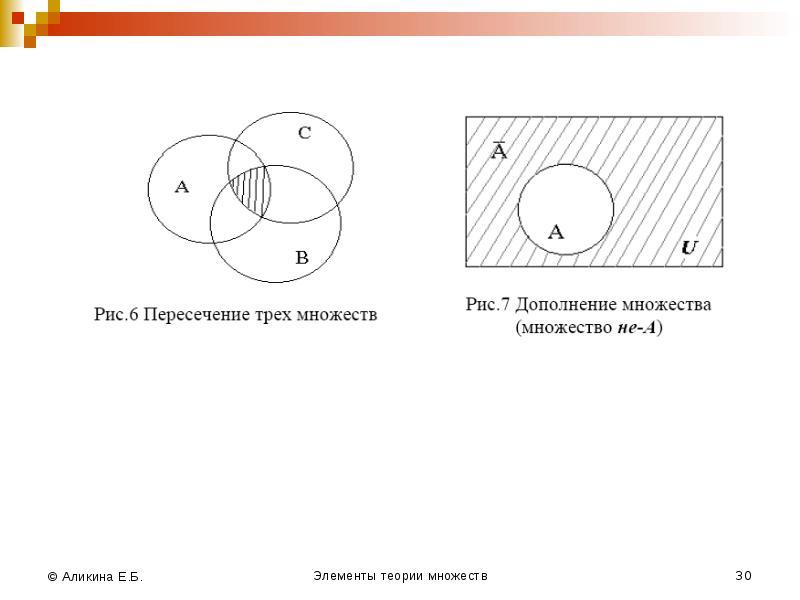 Это совершенно произвольно.
Это совершенно произвольно.
Мы также можем удалить все элементы из набора с помощью метода clear () .
# инициализировать my_set
# Вывод: набор уникальных элементов
my_set = set ("HelloWorld")
печать (my_set)
# выталкиваем элемент
# Вывод: случайный элемент
печать (my_set.pop ())
# добавить другой элемент
my_set.pop ()
печать (my_set)
# очистить my_set
# Вывод: set ()
my_set.Чисто()
печать (my_set)
печать (my_set) Выход
{'H', 'l', 'r', 'W', 'o', 'd', 'e'}
ЧАС
{'r', 'W', 'o', 'd', 'e'}
набор () Операции над наборами Python
Наборы могут использоваться для выполнения математических операций над наборами, таких как объединение, пересечение, разность и симметричная разность. Мы можем сделать это с помощью операторов или методов.
Рассмотрим следующие два набора для следующих операций.
>>> A = {1, 2, 3, 4, 5}
>>> B = {4, 5, 6, 7, 8} Комплект Союза
Set Union в Python Объединение A и B — это набор всех элементов из обоих наборов.
Союз выполняется с использованием | оператор. То же самое можно сделать с помощью метода union () .
# Установить метод объединения
# инициализировать A и B
А = {1, 2, 3, 4, 5}
B = {4, 5, 6, 7, 8}
# использовать | оператор
# Вывод: {1, 2, 3, 4, 5, 6, 7, 8}
печать (A | B) Выход
{1, 2, 3, 4, 5, 6, 7, 8} Попробуйте следующие примеры в оболочке Python.
# использовать функцию объединения
>>> А.союз (B)
{1, 2, 3, 4, 5, 6, 7, 8}
# использовать функцию объединения на B
>>> Б. союз (А)
{1, 2, 3, 4, 5, 6, 7, 8} Установить пересечение
Установить Пересечение в PythonПересечение A и B — это набор элементов, общих для обоих наборов.
Пересечение выполняется с помощью оператора и . То же самое можно сделать с помощью метода пересечение () .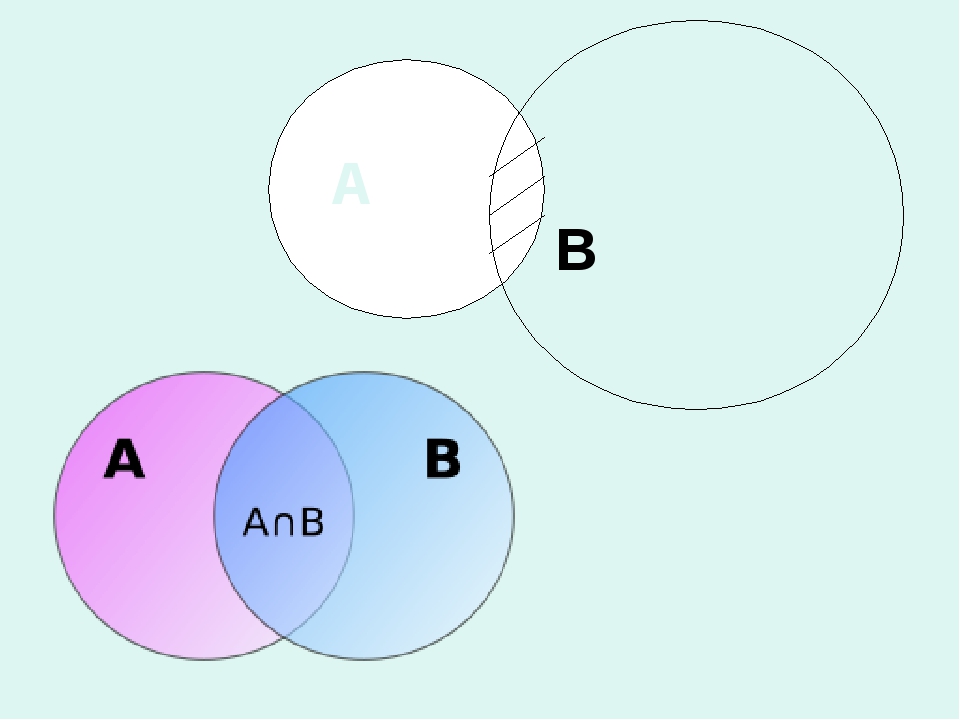
# Пересечение множеств
# инициализировать A и B
А = {1, 2, 3, 4, 5}
B = {4, 5, 6, 7, 8}
# используйте & оператор
# Выход: {4, 5}
печать (A и B) Выход
{4, 5} Попробуйте следующие примеры в оболочке Python.
# использовать функцию пересечения на A
>>> A. пересечение (B)
{4, 5}
# использовать функцию пересечения на B
>>> Б. пересечение (А)
{4, 5} Установить разницу
Set Difference в PythonОтличие набора B от набора A ( A — B ) — это набор элементов, которые есть только в A , но не в B . Аналогично, B — A — это набор элементов в B , но не в A .
Разница выполняется с помощью оператора - . То же самое можно сделать с помощью метода difference () .
# Разница двух наборов
# инициализировать A и B
А = {1, 2, 3, 4, 5}
B = {4, 5, 6, 7, 8}
# использовать - оператор на A
# Вывод: {1, 2, 3}
печать (A - B) Выход
{1, 2, 3} Попробуйте следующие примеры в оболочке Python.
# использовать функцию разницы на A
>>> А.Б) Выход
{1, 2, 3, 6, 7, 8} Попробуйте следующие примеры в оболочке Python.
# использовать функцию symric_difference на A
>>> A.symmetric_difference (B)
{1, 2, 3, 6, 7, 8}
# использовать функцию symric_difference на B
>>> B.symmetric_difference (A)
{1, 2, 3, 6, 7, 8} Другие методы набора Python
Существует множество методов набора, некоторые из которых мы уже использовали выше.Вот список всех методов, доступных для заданных объектов:
| Метод | Описание |
|---|---|
| доб. () | Добавляет элемент в набор |
| прозрачный () | Удаляет все элементы из набора |
| копия () | Возвращает копию набора |
| разница () | Возвращает разницу двух или более наборов как новый набор |
| difference_update () | Удаляет все элементы другого набора из этого набора |
| отказаться () | Удаляет элемент из набора, если он является членом. (Ничего не делать, если элемент не установлен) (Ничего не делать, если элемент не установлен) |
| пересечение () | Возвращает пересечение двух наборов как новый набор |
| crossction_update () | Обновляет набор с помощью пересечения себя и другого |
| isdisjoint () | Возвращает Истина , если два набора имеют нулевое пересечение |
| issubset () | Возвращает Истина , если другой набор содержит этот набор |
| Issueperset () | Возвращает Истина , если этот набор содержит другой набор |
| поп () | Удаляет и возвращает произвольный элемент набора.Вызывает KeyError , если набор пуст |
| удалить () | Удаляет элемент из набора. Если элемент не является членом, вызывает KeyError |
| симметричная_разница () | Возвращает симметричную разность двух наборов как новый набор |
| simric_difference_update () | Обновляет набор с симметричной разницей между собой и другим |
| штуцер () | Возвращает объединение наборов в новый набор |
| обновить () | Обновляет набор с объединением себя и других |
Прочие операции с наборами
Установить тест на членство
Мы можем проверить, существует ли элемент в наборе или нет, используя ключевое слово in .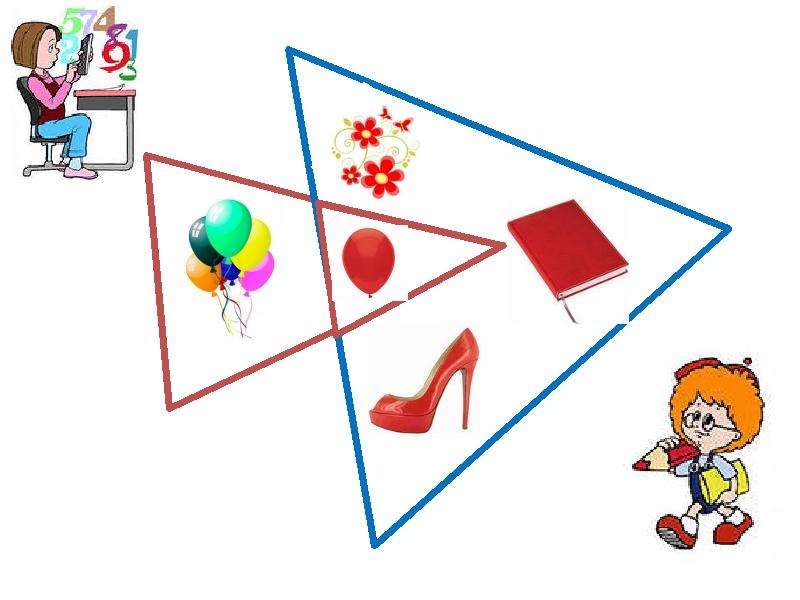
# ключевое слово в наборе
# инициализировать my_set
my_set = set ("яблоко")
# проверяем, присутствует ли 'a'
# Вывод: True
print ('a' в my_set)
# проверяем, присутствует ли 'p'
# Вывод: Ложь
print ('p' отсутствует в my_set) Выход
Верно Ложь
Итерация набора
Мы можем перебирать каждый элемент в наборе, используя цикл для .
>>> для буквы в наборе ("яблоко"):
... печать (письмо)
...
а
п
е
л Встроенные функции с набором
Встроенные функции, такие как all () , any () , enumerate () , len () , max () , min () , sorted () , sum () и т. Д. Обычно используются с наборами для выполнения различных задач.
| Функция | Описание |
|---|---|
| все () | Возвращает True , если все элементы набора истинны (или если набор пуст). |
| любой () | Возвращает True , если какой-либо элемент набора истинен. Если набор пуст, возвращает Ложь . |
| перечислить () | Возвращает перечисляемый объект. Он содержит индекс и значение для всех элементов набора в виде пары. |
| лён () | Возвращает длину (количество элементов) в наборе. |
| макс. () | Возвращает самый крупный элемент в наборе. |
| мин () | Возвращает наименьший элемент в наборе. |
| отсортировано () | Возвращает новый отсортированный список из элементов в наборе (не сортирует сам набор). |
| сумма () | Возвращает сумму всех элементов в наборе. |
Питон Frozenset
Frozenset — это новый класс, имеющий характеристики набора, но его элементы нельзя изменить после назначения.В то время как кортежи являются неизменяемыми списками, frozensets — неизменяемыми наборами.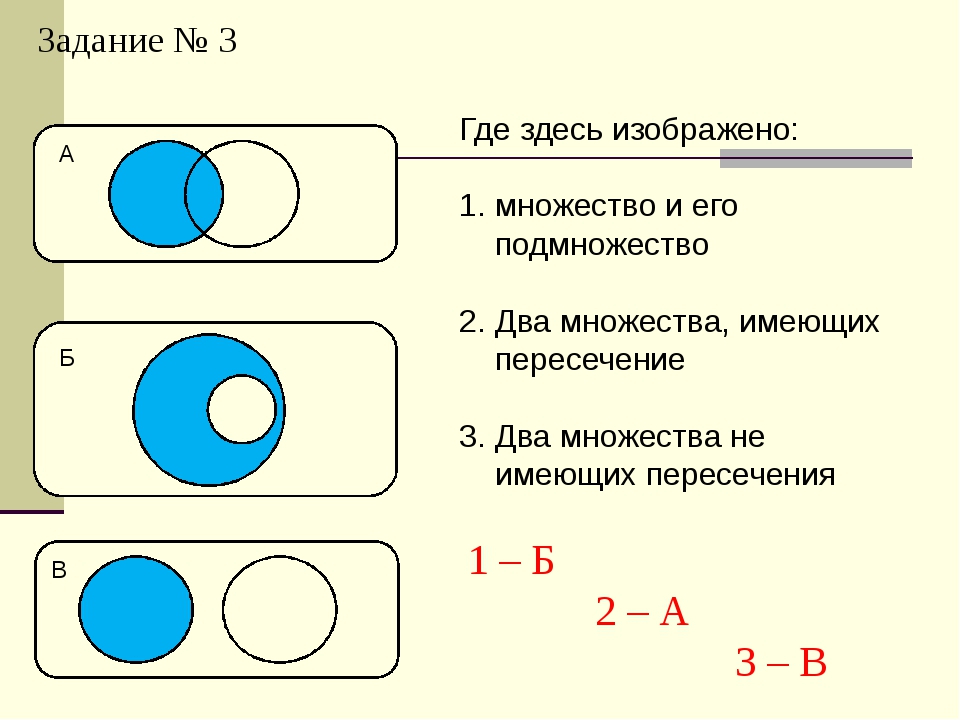
Изменяемые наборы не могут быть хешированы, поэтому их нельзя использовать в качестве ключей словаря. С другой стороны, frozensets хешируются и могут использоваться как ключи к словарю.
Frozensets можно создать с помощью функции frozenset ().
Этот тип данных поддерживает такие методы, как copy () , Difference () , correction () , isdisjoint () , issubset () , Issueperset () , Simric_difference () и союз () .Будучи неизменным, он не имеет методов для добавления или удаления элементов.
# Frozensets
# инициализировать A и B
A = frozenset ([1, 2, 3, 4])
B = замораживание ([3, 4, 5, 6]) Попробуйте эти примеры в оболочке Python.
>>> A.isdisjoint (B)
Ложь
>>> A. разница (B)
Frozenset ({1, 2})
>>> A | B
Frozenset ({1, 2, 3, 4, 5, 6})
>>> A.add (3)
...
AttributeError: объект 'frozenset' не имеет атрибута 'add' Python Set пересечение ()
Пересечение двух или более наборов — это набор элементов, общих для всех наборов.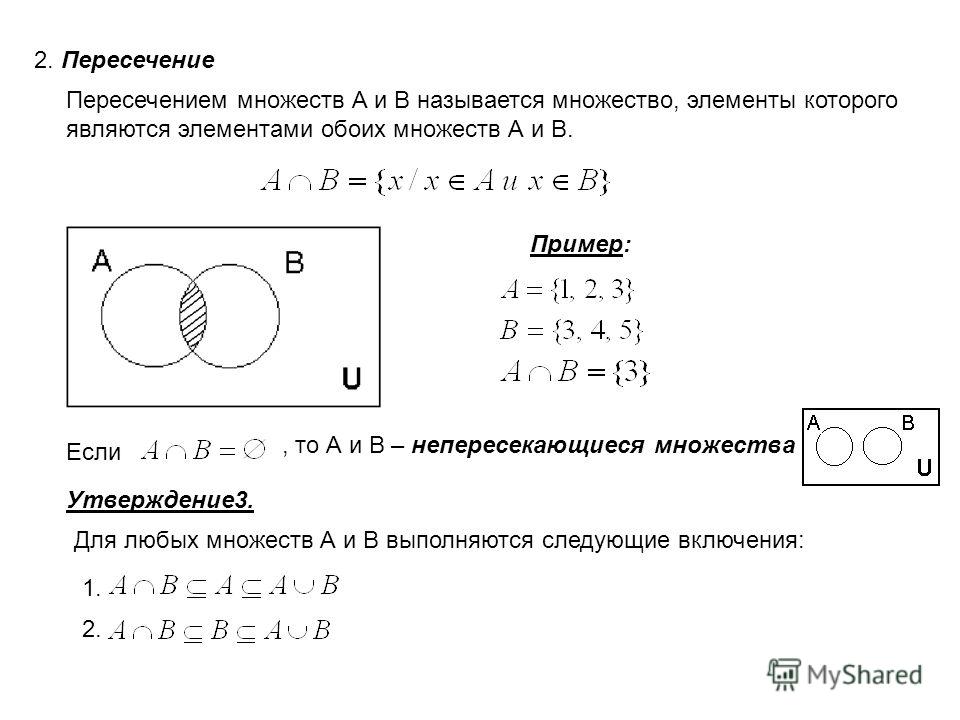 Например:
Например:
А = {1, 2, 3, 4}
B = {2, 3, 4, 9}
C = {2, 4, 9 10}
Потом,
A∩B = B∩A = {2, 3, 4}
A∩C = C∩A = {2, 4}
B∩C = C∩B = {2, 4, 9}
A∩B∩C = {2, 4} Пересечение трех множеств Синтаксис перекрестка () в Python:
A. пересечение (* other_sets)
перекресток () Параметры
пересечение () допускает произвольное количество аргументов (наборов).
Примечание. * не является частью синтаксиса.Он используется, чтобы указать, что метод допускает произвольное количество аргументов.
Возвращаемое значение из пересечения ()
correction () метод возвращает пересечение набора A со всеми наборами (переданными в качестве аргумента).
Если аргумент не передан в пересечение () , он возвращает частичную копию набора ( A ).
Пример 1. Как работает перекресток ()?
A = {2, 3, 5, 4}
B = {2, 5, 100}
C = {2, 3, 8, 9, 10}
печать (B. пересечение (A))
печать (B. пересечение (C))
печать (A. пересечение (C))
печать (C. пересечение (A, B))
пересечение (A))
печать (B. пересечение (C))
печать (A. пересечение (C))
печать (C. пересечение (A, B)) Выход
{2, 5}
{2}
{2, 3}
{2} Другие примеры
A = {100, 7, 8}
B = {200, 4, 5}
C = {300, 2, 3}
D = {100, 200, 300}
печать (A. пересечение (D))
печать (B. пересечение (D))
печать (C. пересечение (D))
print (A. пересечение (B, C, D)) Выход
{100}
{200}
{300}
набор () Вы также можете найти пересечение множеств с помощью оператора и .
Пример 3: Установить пересечение с помощью оператора &
A = {100, 7, 8}
B = {200, 4, 5}
C = {300, 2, 3, 7}
D = {100, 200, 300}
печать (A и C)
печать (A и D)
печать (A, C и D)
печать (A, B, C и D) Выход
{7}
{100}
набор()
набор () Набор— JavaScript | MDN
Объект Set позволяет хранить уникальные значения любого типа, будь то примитивные значения или ссылки на объекты.
Набор объектов представляет собой набор значений. Вы можете перебирать элементы набора в порядке вставки. Значение в Set может встречаться только один раз ; он уникален в коллекции Set .
Равенство значений
Поскольку каждое значение в наборе Set должно быть уникальным, будет проверяться равенство значений. В более ранней версии спецификации ECMAScript это не было основано на том же алгоритме, который использовался в операторе === .В частности, для Set s, +0 (что строго равно -0 ) и -0 были разными значениями. Однако это было изменено в спецификации ECMAScript 2015. Подробнее см. «Равенство ключей для -0 и 0» в таблице совместимости браузеров.
NaN и undefined также могут быть сохранены в Set. Все значения NaN приравниваются (т.е. NaN считается таким же, как NaN , хотя NaN! == NaN ).
-
Комплект () - Создает новый объект
Set.
-
Set.prototype.add ( значение ) - Добавляет значение
Set. Возвращает объектSetс добавленным значением. -
Set.prototype.clear () - Удаляет все элементы из объекта
Set. -
Set.prototype.delete (значение ) - Удаляет элемент, связанный со значением
Set.prototype.has ( значение )впоследствии вернетfalse. -
Set.prototype.has ( значение ) - Возвращает логическое значение, подтверждающее, присутствует ли элемент с заданным значением в объекте
Setили нет.
Итерационные методы
-
Set. prototype [@@ iterator] ()
prototype [@@ iterator] () - Возвращает новый объект итератора, который возвращает значения для каждого элемента в объекте
Setв порядке вставки. -
Set.prototype.keys () - Возвращает новый объект итератора, который возвращает значения для каждого элемента в объекте
Setв порядке вставки. (Для Наборов это то же самое, что и методvalues ().) -
Set.prototype.values () - Возвращает новый объект итератора, который возвращает значения для каждого элемента в объекте
Setв порядке вставки. (Для наборов это то же самое, что и методkeys ().) -
Set.prototype.entries () Возвращает новый объект итератора, который содержит массив из
[ значение , значение ]для каждого элемента в объектеSetв порядке вставки.
Это похоже на объект
Map, так что ключ каждой записи совпадает с его значением для набораSet.-
Set.prototype.forEach ( callbackFn [, thisArg ]) - Вызывает
callbackFnодин раз для каждого значения, присутствующего в объектеSet, в порядке вставки.Если указан параметрthisArg, он будет использоваться как значение, этодля каждого вызоваcallbackFn.
Использование объекта Set
let mySet = new Set ()
mySet.add (1)
mySet.add (5)
mySet.add (5)
mySet.add ('какой-то текст')
пусть o = {a: 1, b: 2}
mySet.add (o)
mySet.add ({a: 1, b: 2})
mySet.has (1)
mySet.has (3)
mySet.has (5)
mySet.имеет (Math.sqrt (25))
mySet.has ('Некоторый текст'.toLowerCase ())
mySet.has (o)
mySet.size
mySet.delete (5)
mySet.has (5)
mySet.size
console. log (mySet)
log (mySet)
Итерационные наборы
для (пусть элемент mySet) console.log (элемент)
для (пусть элемент mySet.keys ()) console.log (элемент)
для (пусть элемент mySet.values ()) console.log (элемент)
for (let [ключ, значение] mySet.entries ()) console.log (ключ)
пусть myArr = Array.from (mySet)
mySet.add (документ.тело)
mySet.has (document.querySelector ('тело'))
mySet2 = новый набор ([1, 2, 3, 4])
mySet2.size
[... mySet2]
let crossction = new Set ([... set1] .filter (x => set2.has (x)))
let difference = new Set ([... set1] .filter (x =>! set2.has (x)))
mySet.forEach (функция (значение) {
console.log (значение)
})
Реализация операций основного набора
function isSuperset (set, subset) {
для (пусть элемент подмножества) {
если (! установить.has (elem)) {
вернуть ложь
}
}
вернуть истину
}
function union (setA, setB) {
let _union = новый набор (setA)
for (пусть elem из setB) {
_union. add (elem)
}
return _union
}
пересечение функций (setA, setB) {
пусть _intersection = новый Set ()
for (пусть elem из setB) {
if (setA.has (elem)) {
_intersection.add (elem)
}
}
return _intersection
}
function symricDifference (setA, setB) {
let _difference = новый набор (setA)
for (пусть elem из setB) {
если (_difference.has (elem)) {
_difference.delete (элемент)
} else {
_difference.add (элемент)
}
}
вернуть _difference
}
разница функций (setA, setB) {
let _difference = новый набор (setA)
for (пусть elem из setB) {
_difference.delete (элемент)
}
вернуть _difference
}
пусть setA = new Set ([1, 2, 3, 4])
пусть setB = новый Set ([2, 3])
пусть setC = new Set ([3, 4, 5, 6])
isSuperset (setA, setB)
объединение (setA, setC)
пересечение (setA, setC)
symricDifference (setA, setC)
разница (setA, setC)
add (elem)
}
return _union
}
пересечение функций (setA, setB) {
пусть _intersection = новый Set ()
for (пусть elem из setB) {
if (setA.has (elem)) {
_intersection.add (elem)
}
}
return _intersection
}
function symricDifference (setA, setB) {
let _difference = новый набор (setA)
for (пусть elem из setB) {
если (_difference.has (elem)) {
_difference.delete (элемент)
} else {
_difference.add (элемент)
}
}
вернуть _difference
}
разница функций (setA, setB) {
let _difference = новый набор (setA)
for (пусть elem из setB) {
_difference.delete (элемент)
}
вернуть _difference
}
пусть setA = new Set ([1, 2, 3, 4])
пусть setB = новый Set ([2, 3])
пусть setC = new Set ([3, 4, 5, 6])
isSuperset (setA, setB)
объединение (setA, setC)
пересечение (setA, setC)
symricDifference (setA, setC)
разница (setA, setC)
Связь с объектами массива
let myArray = ['value1', 'value2', 'value3']
пусть mySet = новый набор (myArray)
mySet. имеет ('значение1')
console.log ([... mySet])
имеет ('значение1')
console.log ([... mySet])
Удалить повторяющиеся элементы из массива
числа const = [2,3,4,4,2,3,3,4,4,5,5,6,6,7,5,32,3,4,5]
console.log ([... новый набор (числа)])
Связь со строками
Пример: пересечение множеств
Цели этой лекции:
Цели этой лекции: Понять механизмы передачи аргументов по значению и по ссылке в C ++ Понимать использование массивов C ++ Понимать, как массивы передаются функциям C ++ Вызов по значению
Дополнительная информацияОсновы потоков ввода-вывода и файлового ввода-вывода
Основы Это похоже на шпаргалку по файловому вводу-выводу в C ++. Он суммирует шаги, которые необходимо предпринять для выполнения базового ввода-вывода в файлы и из файлов, с небольшими пояснениями. Не заменяет чтение
Он суммирует шаги, которые необходимо предпринять для выполнения базового ввода-вывода в файлы и из файлов, с небольшими пояснениями. Не заменяет чтение
Переход с C ++ на VBA
Введение Колледж инженерии и информатики Машиностроительный факультет Машиностроение 309 Численный анализ инженерных систем Осень 2014 г. Номер: 15237 Преподаватель: Ларри
Дополнительная информацияПримечания к лекции 2: Поток управления
6.096 Введение в C ++ Январь 2011 г. Массачусетский технологический институт Лекция Джона Марреро 2 Примечания: Поток управления 1 Мотивация Обычно программа выполняет операторы от первого до последнего.
Дополнительная информацияВведение в Java
Введение в Java Программа HelloWorld Примитивные типы данных Присваивание и арифметические операции Пользовательский ввод Условные операторы Циклические массивы CSA0011 Matthew Xuereb 2008 1 Обзор Java A high
Дополнительная информация Пока петля. 6. Итерация
6. Итерация
Цикл в то время как цикл 1 Цикл — структура управления, которая заставляет набор операторов выполняться повторно (повторяется). Оператор while — наиболее универсальный тип цикла в C ++ false, а логическое выражение true
Дополнительная информацияПередача одномерных массивов функциям.
Передача одномерных массивов функциям. В C ++ массивы могут быть только ссылочными параметрами. Невозможно передать массив по значению.Поэтому амперсанд (&) опускается. Что фактически передается в функцию,
Дополнительная информация6. Структуры управления
— 35 — Управляющие структуры: 6. Управляющие структуры Программа обычно не ограничивается линейной последовательностью инструкций. Во время своего процесса он может раздваиваться, повторять код или принимать решения. Для этого
Дополнительная информацияФункции-члены класса istream
Функции-члены класса istream Оператор извлечения имеет ограниченное применение, потому что он всегда использует пробелы для ограничения чтения входящего потока. Его нельзя использовать для чтения этих пробельных символов,
Его нельзя использовать для чтения этих пробельных символов,
Глава 8 Выбор 8-1
Глава 8 Выбор 8-1 Выбор (Решение) Вторая логическая структура управления — это выбор: Выбор Выбор между двумя или более альтернативными действиями. Операторы выбора изменяют последовательный поток
Дополнительная информацияРешение проблем с помощью C ++
Отделгеоматики Eng. Телефон Тегеранского университета: 0912 132 5823 Электронная почта: [email protected] http://www.marajabi.com Незавершенные бизнес-описания (принуждение к определенному типу выражения) #include
Дополнительная информацияОтветы на мини-викторины и лабораторные работы
Ответы Ответы на мини-викторины и лабораторные работы Ответы на главу 1 Мини-викторины Мини-викторины 1-1 1. Машина 2. a. процедурно-ориентированный 3. b. объектно-ориентированный 4. компилятор Мини-викторина 1-2 1.последовательность, выбор, повтор
Машина 2. a. процедурно-ориентированный 3. b. объектно-ориентированный 4. компилятор Мини-викторина 1-2 1.последовательность, выбор, повтор
Объектно-ориентированный дизайн программного обеспечения
Объектно-ориентированное программное обеспечение. Введение в Java — II. Джузеппе Липари http://retis.sssup.it/~lipari Scuola Superiore Sant Anna Pisa 28 октября 2010 г. Г. Липари (Scuola Superiore Sant Anna) Введение
Дополнительная информацияОбъектно-ориентированный дизайн программного обеспечения
Объектно-ориентированный дизайн программного обеспечения. Введение в Java — II. Джузеппе Липари. Http: // retis.sssup.it/~lipari Scuola Superiore Sant Anna, Пиза, 14 сентября 2011 г. Г. Липари (Scuola Superiore Sant Anna) Введение
Дополнительная информацияУчебник по Visual C ++ 2010
Учебное пособие по Visual C ++ 2010 Осень, 2011 г. Оглавление Страница Без введения ————————————- —————————— 2 Демонстрация однофайловой программы ——— —— ————————————
Оглавление Страница Без введения ————————————- —————————— 2 Демонстрация однофайловой программы ——— —— ————————————
В этой главе вы узнаете:
А теперь иди, напиши это перед ними в таблице и запиши в книгу.Исаия 30: 8 Идти дальше — так же неправильно, как и проиграть. Конфуций Начните с начала и продолжайте, пока не дойдете до конца; затем остановитесь. Льюис
Дополнительная информацияОтветы на избранные упражнения
DalePhatANS_complete 18.08.04 10:30 Страница 1049 Ответы на избранные упражнения Глава 1 Упражнения для подготовки к экзамену 1. a. v, b. IC. viii, г. iii, e. iv, f. vii, g. vi, h. II. 2. Анализ и спецификация,
Дополнительная информацияФункции и передача параметров
Глава 5: Функции и передача параметров В этой главе мы исследуем разницу между вызовами функций в C и C ++ и, как следствие, разницу в способах определения функций на двух языках.
Условные (с решениями)
Условные выражения (с решениями) Для упражнений с 1 по 27 укажите результат, который будет получен. Предположим, что следующие объявления: final int MAX = 25, LIMIT = 100; int num1 = 12, num2 = 25, num3 = 87;
Дополнительная информацияГлава 5. Выбор 5-1
Глава 5 Выбор 5-1 Выбор (Решение) Вторая логическая структура управления — это выбор: Выбор Выбор между двумя или более альтернативными действиями.Операторы выбора изменяют последовательный поток
Дополнительная информацияВвод / вывод C ++: потоки
Ввод / вывод C ++: потоки 1 Основным типом данных для ввода / вывода в C ++ является поток. C ++ включает сложную иерархию типов потоков. Самыми основными типами потоков являются стандартные потоки ввода / вывода: istream
Дополнительная информация ПРАКТИЧЕСКИЙ ЭКЗАМЕН ПО C ++ FA 5. 1
1
С ++ FA 5.1 ПРАКТИЧЕСКИЙ СРЕДНИЙ ЭКЗАМЕН Этот практический промежуточный экзамен охватывает разделы от C ++ FA 1.1 до C ++ FA 1.4 языка C ++ с финансовыми приложениями от Бена Ван Влиета, доступные на сайте www.benvanvliet.net. 1.) Указатель
Дополнительная информацияОсновы программирования VB.NET
Глава 3 Цели Основы программирования В этой главе вы: Изучите язык программирования. Напишите определение модуля. Используйте переменные и типы данных. Вычислите с помощью Записывайте операторы принятия решений.
. Дополнительная информацияИспользование двумерных массивов
Использование двумерных массивов Отличные новости! То, что раньше было старым одноэтажным мотелем Java, только что отремонтировали! В новом пятиэтажном отеле Java сервируется бесплатный континентальный завтрак, а номер
— абсолютно бесплатный. Дополнительная информация
Дополнительная информация Программа расчета заработной платы.Начисление заработной платы
Программа 1 Следующий пример представляет собой простую программу расчета заработной платы, которая иллюстрирует большинство основных элементов языка C ++, описанных в разделах с 3 по 6 примечаний к курсу. В течение срока формальный
Дополнительная информацияСтруктуры данных CSI33
План факультета математики и информатики Общественный колледж Бронкса 25 ноября 2015 г. Краткое содержание 1 Глава 12: Шаблоны C ++ Краткое содержание Глава 12: Шаблоны C ++ 1 Глава 12: Шаблоны C ++
Дополнительная информацияПодводные камни встраиваемого ПО
Подводные камни встраиваемого ПО..и как их избежать Sagar Behere 31 марта 2014 г. Ловушки встраиваемого ПО 1/19 Что не так с этим кодом? число без знака int = BigValue; для (int i = 0; i 1 7 JavaScript: управляющие операторы I 7. 15 Указатели и связанные списки 15.1 Узлы и связанные списки 828 узлов 828 Связанные списки 834 Вставка узла в начало списка 835 Ловушка: потеря узлов 839 Поиск в связанном списке 840 указателей в качестве итераторов АЛГОРИТМЫ И СТРОИТЕЛЬСТВА Типичную задачу программирования можно разделить на две фазы: Этап решения проблемы создает упорядоченную последовательность шагов, описывающих решение проблемы, эта последовательность шагов jfe_ch04_7. Глава 9 Делегаты и события Две языковые функции являются центральными для использования the.net FCL. Мы использовали как делегатов, так и события в темах, которые мы обсуждали до сих пор, но я не исследовал Стеки Линейные структуры данных Коллекция компонентов, которые могут быть расположены в виде прямой линии. Структура данных увеличивается или уменьшается по мере добавления или удаления объектов. ADT обеспечивают абстрактный слой для различных операций Глава 7 Функции 7-1 Функции Модули в C ++ называются функциями. Использование функций в программе позволяет разбить программу на небольшие задачи.- программа для написания и отладки ECE114 L / 256 Руководство Тим Лин и Саид Монеми Государственный политехнический университет Калифорнии в Помоне Департамент электротехники и вычислительной техники Руководство лаборатории программирования C / C ++ Доктор Тим Лин Доктор Саид Монеми EP241 Компьютерное программирование Тема 10 Базовые классы Департамента инженерной физики Газиантепский университет Веб-страница курса www.gantep.edu.tr/~bingul/ep241 сентябрь 2013 г. Sayfa 1 Введение В этой лекции Приведенный ниже вопрос является вопросом для решения количественной задачи GMAT по теории множеств. JavaScript: управляющие операторы I
 1 Введение 2 Методы, которые вы здесь изучите, применимы к большинству языков высокого уровня, включая JavaScript 1 7.2 Алгоритмы 3 Любая вычислимая проблема может быть
1 Введение 2 Методы, которые вы здесь изучите, применимы к большинству языков высокого уровня, включая JavaScript 1 7.2 Алгоритмы 3 Любая вычислимая проблема может быть Указатели и связанные списки
Алгоритмы и схемы
ПЕТЛИ ГЛАВА ГЛАВА ЦЕЛИ
 fm Page 139 Пятница, 8 мая 2009 г. 14:45 ЦИКЛЫ ГЛАВА 4 ЦЕЛИ ГЛАВЫ Узнать о циклах while, for и do Ознакомиться с алгоритмами общих циклов Чтобы понять вложенные циклы Реализовать
fm Page 139 Пятница, 8 мая 2009 г. 14:45 ЦИКЛЫ ГЛАВА 4 ЦЕЛИ ГЛАВЫ Узнать о циклах while, for и do Ознакомиться с алгоритмами общих циклов Чтобы понять вложенные циклы Реализовать Глава 9 Делегаты и события
Стеки.Линейные структуры данных
Глава 7.
 Функции 7-1
Функции 7-1 Руководство лаборатории программирования C / C ++
EP241 Компьютерное программирование
GMAT Практика теории множеств,: Пересечение, объединение 3 пересекающихся сетов: Wizako GMAT coaching
 Концепция: Найдите объединение 3-х перекрывающихся множеств, а затем его дополнение.
Концепция: Найдите объединение 3-х перекрывающихся множеств, а затем его дополнение. Вопрос: В классе из 120 учеников с номерами от 1 до 120 все четные ученики выбирают физику, те, чьи числа делятся на 5, выбирают химию, а те, чьи числа делятся на 7, выбирают математику.Кто не выбирает ни один из трех предметов?
- 19
- 41
- 21
- 57
- 26
Пояснительный ответ
Видео-объяснение будет скоро добавлено Подход: Давайте найдем количество студентов, которые взяли хотя бы один из трех предметов, и вычтем результат из общего числа 120, чтобы получить количество студентов, которые не выбрали ни один из трех предметов.
Число студентов, которые изучали хотя бы один из трех предметов, можно узнать, найдя n (AUBUC), где A — это набор студентов, изучавших физику, B — набор студентов, изучавших химию, а C — набор студентов, изучавших химию. студенты, выбравшие математику.
Теперь n (A \ чашка) B \ чашка) C) = n (A) + n (B) + n (C) — {n (A \\ cap) B) + n (B \\ cap ) C) + n (C \ cap) A)} + n (A \ cap) B \ cap) C)
A — это набор выбравших Physics = \\ frac {120} {2}) = 60 студентов
B — это набор тех, кто выбрал химию = \\ frac {120} {5}) = 24
C — это набор тех, кто выбрал Math = \\ frac {120} {7}) = 17.
Количество студентов, выбравших физико-химию
Студенты, число которых кратно 2 и 5, т.е. общее кратное 2 и 5, выбрали бы как физику, так и химию.
НОК 2 и 5 будет первым числом, кратным 2 и 5. т. Е. 10 — это первое число, которое будет частью обеих серий.
10 -й , 20 -й , 30 -й ….. пронумерованные студенты или каждый 10-й студент, начиная с 10-го, выбрали бы и физику, и химию.
Следовательно, n (A \ cap) B) = \ frac {120} {10}) = 12
Количество студентов, выбравших физико-математический факультет
Студенты, чьи числа кратны 2 и 7, т. Е. Кратны 2 и 7, выбрали бы как физику, так и математику.
НОК 2 и 7 будет первым числом, кратным 2 и 7.т.е. 14 — это первое число, которое будет частью обеих серий.
14 -й , 28 -й , 42 -й ….. пронумерованные студенты или каждый 14-й студент, начиная с 14-го, выбрал бы физику и математику.
Следовательно, n (C \ cap) A) = \ frac {120} {14}) = 8
Количество студентов, выбравших химию и математику
Студенты, число которых кратно 5 и 7 i.е., кратные 5 и 7 выбрали бы и химию, и математику.
НОК 5 и 7 будет первым числом, кратным 5 и 7. то есть 35 — первое число, которое будет частью обеих серий.
35 -й , 70 -й …. пронумерованные студенты или каждый 35-й студент, начиная со студента номер 35, выбрал бы химию и математику.
Следовательно, n (B \ cap) C) = \ frac {120} {35}) = 3
Количество студентов, выбравших все 3 предмета
Учащиеся, числа которых кратны 2, 5 и 7 i.е., кратные 2, 5 и 7 были бы выбраны для всех 3 предметов.
НОК 2, 5 и 7 будет первым числом, кратным 2, 5 и 7. т.е. 70 — это первое число, которое будет частью всех трех серий.
70 — единственное кратное 70 в первых 120 натуральных числах. Таким образом, студент с номером 70 — единственный, кто выбрал бы все три предмета.
Следовательно, n (A \ чашка) B \ чашка) C) = 60 + 24 + 17 — (12 + 8 + 3) + 1 = 79.
Количество студентов, которые не выбрали ни один из трех предметов = 120 — 79 = 41.
Вариант B — правильный ответ.
Типы пересечений
Используемый в типах, оператор и создает тип пересечения.
Проверка типа
Тип S & T представляет значения типа S и T одновременно.
признак Сбрасываемый:
def reset (): Единица
черта Growable [T]:
def add (t: T): Единица измерения
def f (x: сбрасываемый и растущий [String]) =
x.reset ()
x.add ("первый")
Параметр x должен быть и , сбрасываемый и Growable [String] .
Все элементы перекрестка типа A и B являются элементами A и всеми элементами B .Например, Resettable & Growable [String] имеет методы членов reset и add .
и — коммутативный : A и B — тот же тип, что и B&A .
Если элемент присутствует как в A, , так и в B , его тип в A и B является пересечением его типа в A и его типа в B . Например, предположим, что определения:
признак A:
def children: Список [A]
черта B:
def children: Список [B]
val x: A & B = новый C
val ys: List [A & B] = x.дети
Тип детей в A и B является пересечением типа детей в A и его типа в B , то есть List [A] & List [B] . Его можно дополнительно упростить до List [A & B] , поскольку List является ковариантным.
Кто-то может задаться вопросом, как компилятор мог придумать определение для дочерних элементов типа List [A & B] , поскольку даны определения дочерних элементов типа List [A] и List [B] .Ответ в том, что компилятору это не нужно. A & B — это просто тип, который представляет набор требований для значений этого типа. В точке, где значение построено , нужно убедиться, что все унаследованные члены определены правильно. Таким образом, если определить класс C , который наследует A и B , необходимо дать в этот момент определение метода children с требуемым типом.
класс C расширяет A, B:
def children: Список [A & B] = ???
Подробнее
.
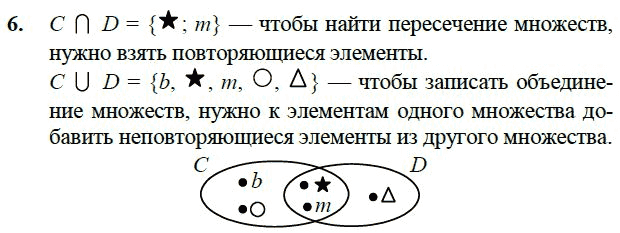


 )
)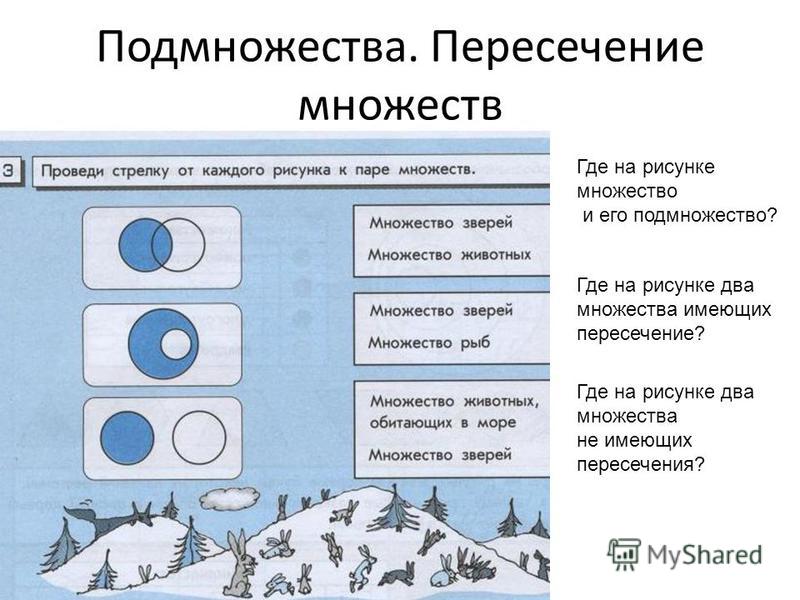 )
)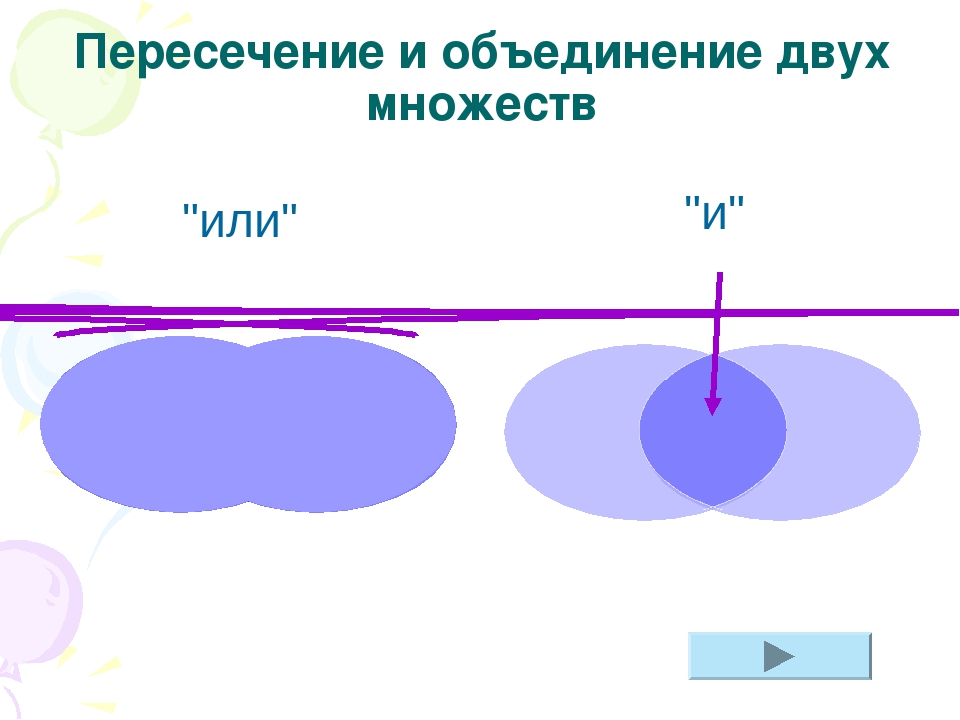 Сделай вывод.
Сделай вывод. )
) )
)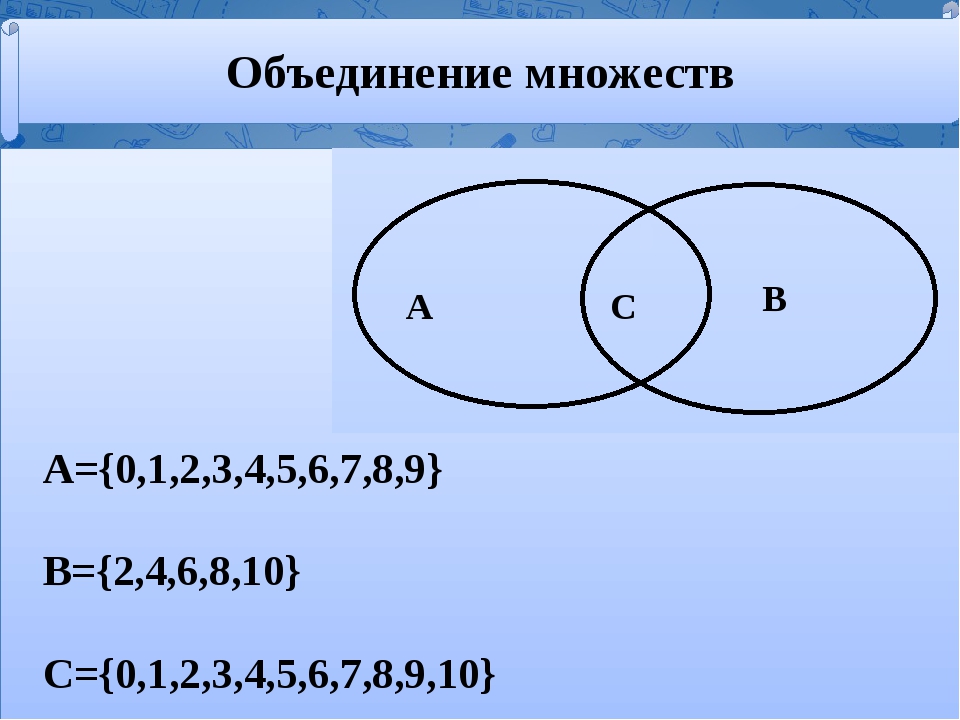
 (Структура учит сконцентрировать внимание на учителе и приготовиться к следующему этапу работы).
(Структура учит сконцентрировать внимание на учителе и приготовиться к следующему этапу работы). (Множество – это группа предметов, объектов или живых существ, собранных вместе)
(Множество – это группа предметов, объектов или живых существ, собранных вместе) Множество волков — … (стая)
Множество волков — … (стая)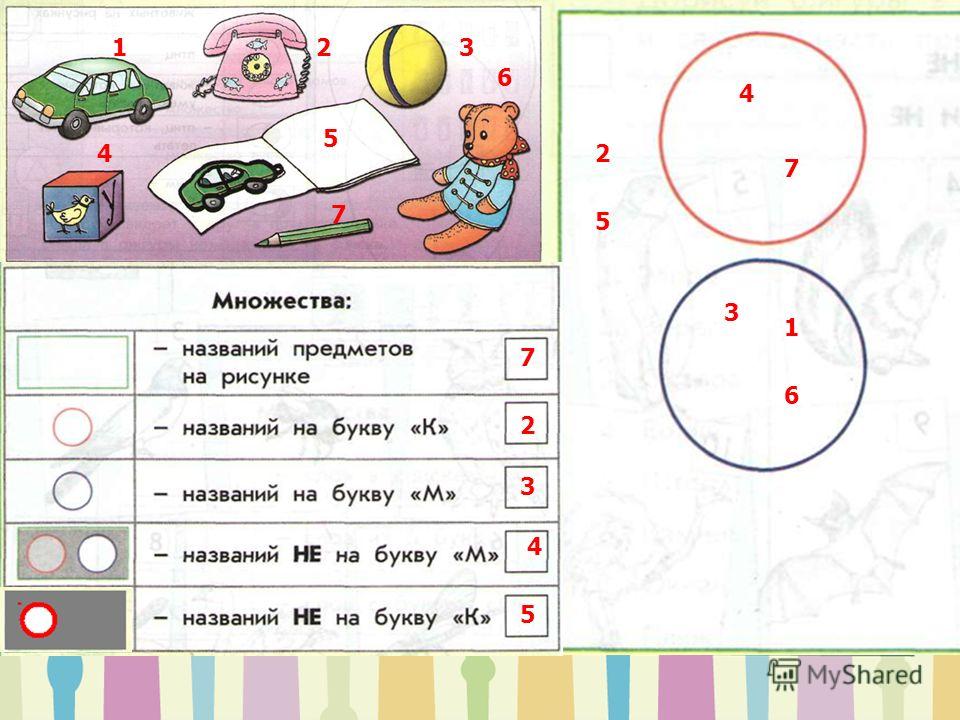

 (зелёные И деревянные объекты)
(зелёные И деревянные объекты) 50
50
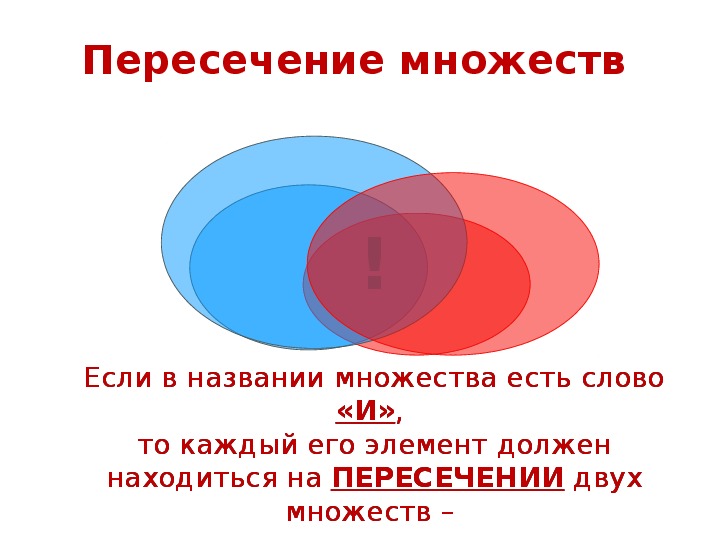

 ).
).


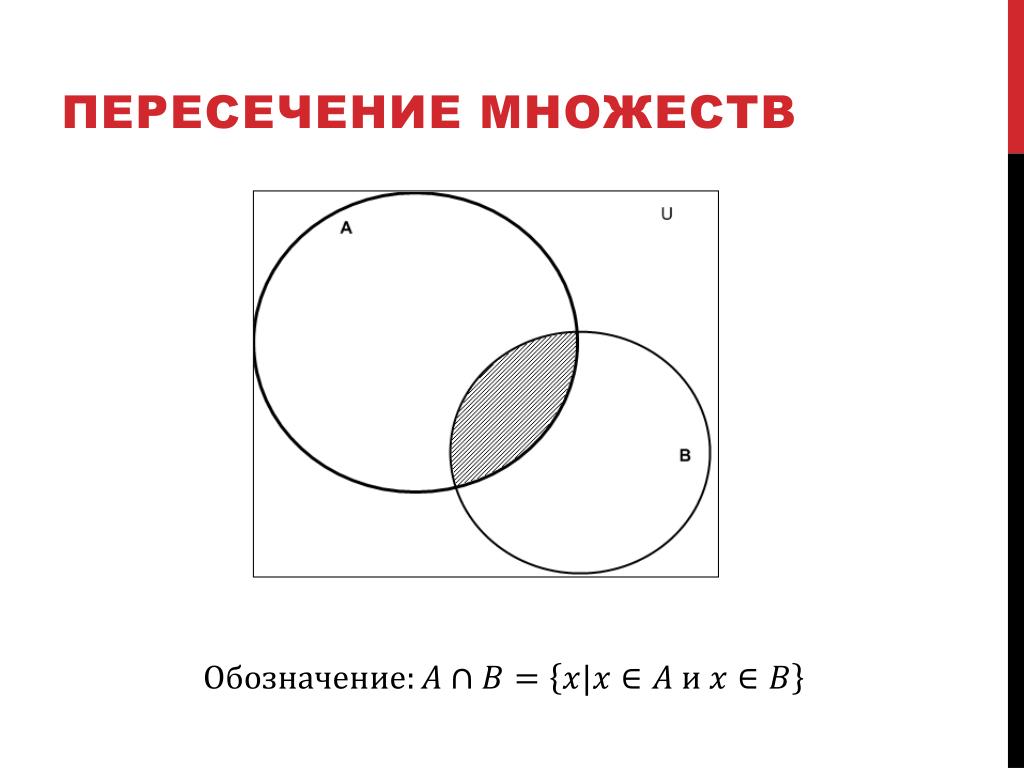 – в созданных совместно с педагогом на уроке ситуациях общения и сотрудничества, опираясь на общие для всех простые правила поведения, делать выбор, как себя вести.
– в созданных совместно с педагогом на уроке ситуациях общения и сотрудничества, опираясь на общие для всех простые правила поведения, делать выбор, как себя вести. 51
51
 пересечение (A))
печать (B. пересечение (C))
печать (A. пересечение (C))
печать (C. пересечение (A, B))
пересечение (A))
печать (B. пересечение (C))
печать (A. пересечение (C))
печать (C. пересечение (A, B))  prototype [@@ iterator] ()
prototype [@@ iterator] () 
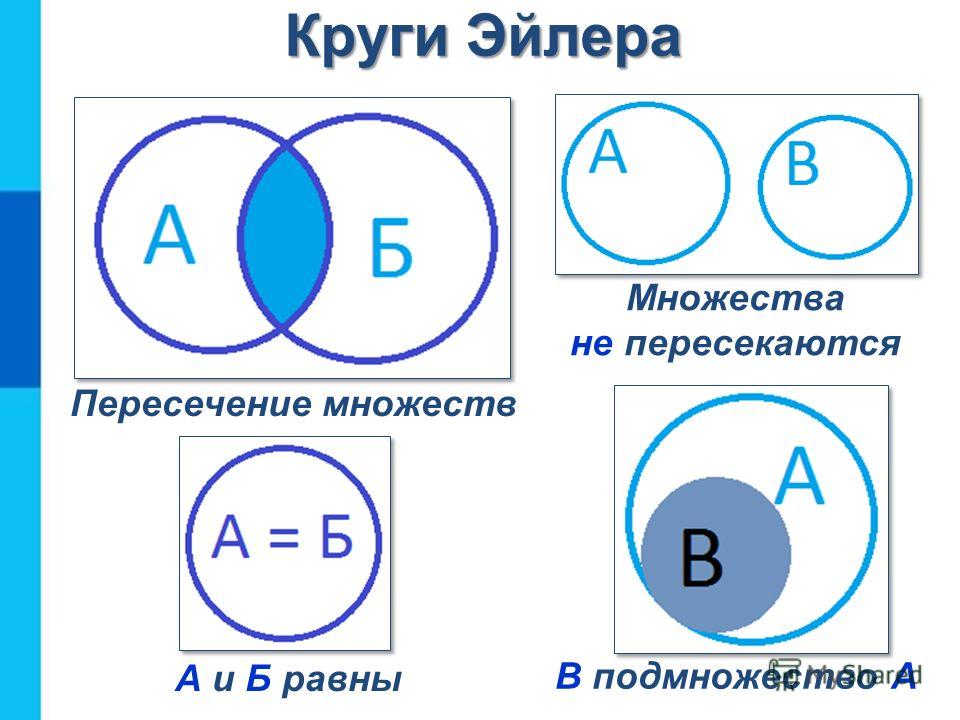 log (mySet)
log (mySet)
 add (elem)
}
return _union
}
пересечение функций (setA, setB) {
пусть _intersection = новый Set ()
for (пусть elem из setB) {
if (setA.has (elem)) {
_intersection.add (elem)
}
}
return _intersection
}
function symricDifference (setA, setB) {
let _difference = новый набор (setA)
for (пусть elem из setB) {
если (_difference.has (elem)) {
_difference.delete (элемент)
} else {
_difference.add (элемент)
}
}
вернуть _difference
}
разница функций (setA, setB) {
let _difference = новый набор (setA)
for (пусть elem из setB) {
_difference.delete (элемент)
}
вернуть _difference
}
пусть setA = new Set ([1, 2, 3, 4])
пусть setB = новый Set ([2, 3])
пусть setC = new Set ([3, 4, 5, 6])
isSuperset (setA, setB)
объединение (setA, setC)
пересечение (setA, setC)
symricDifference (setA, setC)
разница (setA, setC)
add (elem)
}
return _union
}
пересечение функций (setA, setB) {
пусть _intersection = новый Set ()
for (пусть elem из setB) {
if (setA.has (elem)) {
_intersection.add (elem)
}
}
return _intersection
}
function symricDifference (setA, setB) {
let _difference = новый набор (setA)
for (пусть elem из setB) {
если (_difference.has (elem)) {
_difference.delete (элемент)
} else {
_difference.add (элемент)
}
}
вернуть _difference
}
разница функций (setA, setB) {
let _difference = новый набор (setA)
for (пусть elem из setB) {
_difference.delete (элемент)
}
вернуть _difference
}
пусть setA = new Set ([1, 2, 3, 4])
пусть setB = новый Set ([2, 3])
пусть setC = new Set ([3, 4, 5, 6])
isSuperset (setA, setB)
объединение (setA, setC)
пересечение (setA, setC)
symricDifference (setA, setC)
разница (setA, setC)
 имеет ('значение1')
console.log ([... mySet])
имеет ('значение1')
console.log ([... mySet])
 6. Итерация
6. Итерация  1
1