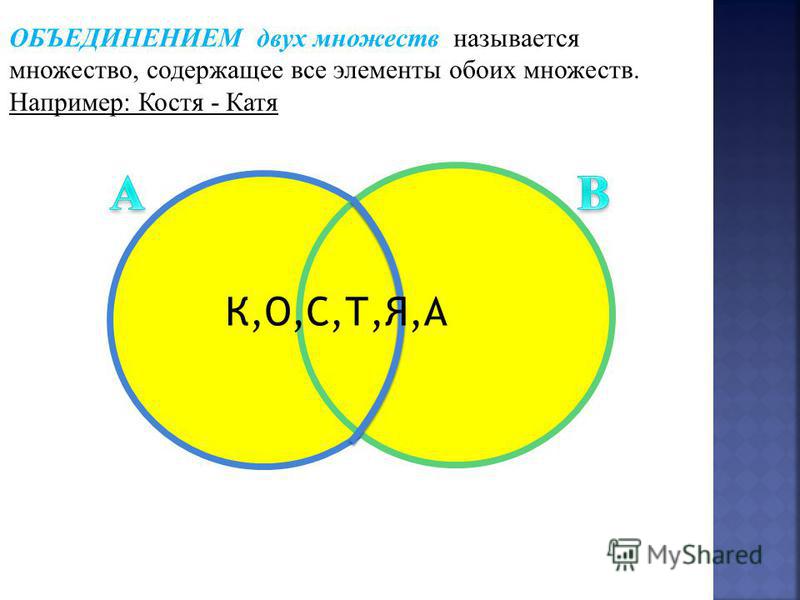
Пересечение и объединение множеств
Вы знаете, ученик третьего класса Максим очень хотел объяснить вам эту тему, но немного приболел и прийти сегодня не смог. Но, благодаря Интернету, мы можем с ним связаться.
̶ Здравствуй Максим!
̶ Здравствуйте! Проверьте, чтобы ваши соседи по парте были готовы к уроку. И мы начинаем.
Прослушайте название пар множеств и попытайтесь заметить, что повторяется в каждой паре.
Животные и герои мультфильмов;
Рыбы и птицы;
Материки и части света;
Звёзды и планеты.
Ну, что заметили? Конечно, повторялся слово «и».
Если в названии множества есть союз «И», то каждый его элемент должен находиться на пересечении двух множеств, т.е. находиться одновременно в двух множествах. Другими словами мы можем сказать, что пересечение множеств

А теперь задание.
Необходимо разместить элементы по своим множествам.
Давайте посмотрим, что за элементы. Так это имена мальчиков и девочек: Коля, Ваня, Даша, Игорь, Катя, Саша, Дима, Юля, Ира, Женя. Будем размещать имена мальчиков в синий прямоугольник, а девочек – в розовый. Ага! Так ведь Сашей и Женей могут звать как мальчиков, так и девочек. Значит, эти два имени будут находиться сразу в двух множествах, т.е. на пересечении двух множеств.
Итак,
Коля, Ваня – это мальчики, помещаем эти элементы во множество имён мальчиков.
Даша – имя девочки, помещаем в розовый прямоугольник, где находятся имена
девочек. Игорь – имя мальчика, Катя – имя девочки. Саша, так могут звать и
мальчика, и девочку, значит, этот элемент будет находиться на пересечении
двух множеств. Дима – элемент из множества имён мальчиков. Юля, Ира,
конечно элементы из множества имён девочек. И последнее имя, Женя, это имя
могут иметь как девочки, так и мальчики. Значит, этот элемент будет находиться на
пересечении двух множеств.
И последнее имя, Женя, это имя
могут иметь как девочки, так и мальчики. Значит, этот элемент будет находиться на
пересечении двух множеств.
Теперь все имена находятся в своих множествах.
А сейчас я прочитаю названия ещё нескольких пар множеств, а вы попытайтесь заметить, что повторяется в этих парах.
Яблоки или груши;
Полевые или садовые цветы;
Попугаи или морские свинки;
Рабочие или выходные дни.
Заметили, что повторялось в парах множеств? Конечно, это слово «или».
Посмотрите ещё раз на названия множеств.
Например, яблоки или груши. А ведь эти множества можно объединить в одно с общим названием «фрукты» и все
Попугаи или морские свинки. Их можно объединить во множество с названием
«домашние
животные» и все попугаи, и все морские свинки будут находиться в новом
множестве.
Значит, если в названии множества есть слово «или», то его элемент может находиться в любом множестве и тогда происходит объединение множеств, т.е. эти множества объединяются.
Давайте рассмотрим два множества: домашние животные, дикие животные.
Множество домашние животные содержат следующие элементы: собака, кошка, морская свинка, попугай.
Множество дикие животные состоит из следующих элементов: бегемот, леопард, волк, лев.
Какой общий признак у элементов этих двух множеств?
Элементы каждого из них относятся с животному миру. Значит, можно, объединив эти множества, создать новое множество под названием животные. Теперь все элементы находятся в одном множестве.А теперь, конечно, задание.
Распределить
элементы по множествам, объединить их и придумать
название для нового множества.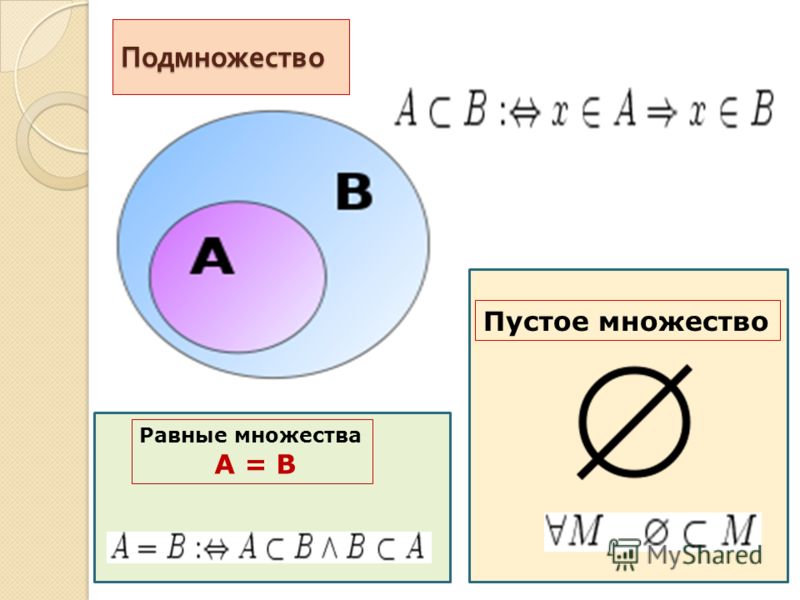
Итак, смотрим на элементы. Ага, у нас два множества: множество стульев и множество столов. Распределяем элементы по множествам. Все элементы стулья во множество стульев, а все элементы столы во множество столов.
Объединяем множества. Какое название будет у нашего нового множества? Множество мебели.
Давайте ещё раз определим разницу между пересечением и объединением множеств
Если в названии множества есть слово «И», то это пересечение, и каждый элемент должен находиться на пересечении двух множеств.
Если в названии множества есть слово «или», то его элемент может находиться в любо области объединённых множеств.
Я надеюсь, что вы поняли разницу между пересечением и объединением множеств. А давайте проверим?
Итак,
перед вами рисунок с тремя множествами.
Множество учеников, которые любят математику, множество учеников, которые любят информатику и множество всех учеников. Но, среди учеников есть и такие, которые любят и математику и информатику. Значит, эти два множества пересекаются и одновременно они являются подмножеством множества всех учеников. А теперь появляются элементы во множествах.
Используя полученные знания сегодня на уроке, будем отвечать на вопросы. А все ответы хранятся на этом рисунке, главное внимательно слушать вопросы и внимательно смотреть на рисунок.
Первый вопрос:
Сколько учеников любят математику? Считаем их во множестве учеников, которые любят математику, и не забываем посчитать тех учеников, которые находятся на пересечении двух множеств учеников, которые любят и математику, и информатику. Считаем. Их шесть.
Сколько
учеников любят информатику? Считаем их во множестве учеников, которые любят
информатику и опять считаем тех учеников, которые находятся на пересечении
двух множеств. Считаем. Их пять.
Считаем. Их пять.
Сколько учеников любят и математику, и информатику? Будем считать тех учеников, которые находятся на
Сколько учеников любят или математику или информатику? Если используется слово «или», значит элементы находятся в любом месте множеств за исключением любителей двух предметов сразу. Значит, считаем учеников и в первом множестве и во втором, но не включаем тех, кто находится в пересечении. Их пять.
Сколько учеников любят только математику? Любят математику только те, которые находятся во множестве учеников, которые любят математику. Ученики, которые находятся на пересечении двух множеств, сюда относится не будут, т.к. они любят и математику, и информатику. Итак, считаем и получается, что 3 ученика любят только математику.
Сколько
учеников любят только информатику? Опять, учеников, которые находятся на пересечении
двух множеств, считать не будем.
Сколько учеников не любят математику? Надо посчитать их во множестве учеников, которые любят информатику, кроме тех, которые находятся на пересечении множеств, т.к. эти ученики любят информатику и математику. А так же надо посчитать тех учеников, которые находятся во множестве всех учеников, т.к. они не любят математику. Их всего 5.
Всем спасибо за отличную работу. Теперь я точно понял, что хочу быть учителем!
Тебе спасибо, Максим. Тему объяснил хорошо. До свидания! А мы ещё сделаем выводы.
Итак.
Множество – это объединение некоторых объектов (элементов) в группу по определённым признакам.
Множество может быть подмножеством другого множества. Например: множество собак является подмножеством множества домашние животные.
Множества
могут пересекаться. Например: множество чисел, которые делятся на
2, и множество чисел, которые делятся на 3, пересекаются, т. к. числа, например,
6 и 12 делится и на 2, и на 3.
к. числа, например,
6 и 12 делится и на 2, и на 3.
Множества могут и не пересекаться. Например: множество телефонов и множество цветов.
И множества могут объединяться. Например: множество рабочих дней недели и множество выходных можно объединить в одно множество дней недели.
Выводы сделаны, и я желаю вам успехов при выполнении заданий!
Имя____________________ Урок математики 7 октября Тема: Объединение и пересечение двух множеств.
2, 47, 16, 8, 17, 32, 6, 53.
_______________________________________________
Алия купила 5 тетрадей по 9 тенге и блокнот за 540 тенге. А Тимур- 4 тетради по 9 тенге и альбом за 345 тенге. Кто из них потратил денег больше и насколько? Задача. Ал. — ? тг, ____________________________________ на ? тг б. Т. — ? тг, ____________________________________ _____________________________________________________ _____________________________________________________ _____________________________________________________ Ответ: ______________________________________________ Домашняя работа. 1.Выучи правила с. 64, 66 о пересечении множеств(А В), объединении множеств (АВ) и о пустом множестве . 2. Реши уравнении. 27 : а = 9 100 – у = 14 а 8 = 24 ___________ _____________ _____________ ___________ _____________ ______________ ___________ _____________ ______________ ___________ _____________ ______________ | Имя____________________ Урок математики 7 октября Тема: Объединение и пересечение двух множеств.
2, 47, 16, 8, 17, 32, 6, 53.
_______________________________________________ 4)Реши задачу. Алия купила 5 тетрадей по 9 тенге и блокнот за 540 тенге. А Тимур- 4 тетради по 9 тенге и альбом за 345 тенге. Кто из них потратил денег больше и насколько? Задача. Ал. — ? тг, ____________________________________ на ? тг б. Т. — ? тг, ____________________________________ _____________________________________________________ _____________________________________________________ _____________________________________________________ Ответ: ______________________________________________ Домашняя работа. 1.Выучи правила с. 64, 66 о пересечении множеств(А В), объединении множеств (АВ) и о пустом множестве . 2. Реши уравнении. 27 : а = 9 100 – у = 14 а 8 = 24 ___________ _____________ _____________ ___________ _____________ ______________ ___________ _____________ ______________ ___________ _____________ ______________ |
Урок «Пересечение и объединение множеств»
Цели урока:
- образовательные: формирование умений выделять множества, подмножества; формирование навыков находить на изображениях область пересечения и объединения множеств и называть элементы из этой области, решать задачи;
- развивающие: развитие познавательного интереса учащихся; развитие интеллектуальной сферы личности, развитие умений сравнивать и обобщать.

- воспитательные: воспитывать аккуратность и внимательность при решении.
1. Организационный момент.
2. Учитель сообщает тему урока, совместно с учащимися формулирует цели и задачи.
3. Учитель совместно с учащимися вспоминает материал, изученный по теме «Множества» в 7 классе, вводит новые понятия и определения, формулы для решения задач.
<Приложение1.ppt>
«Множество есть многое, мыслимое нами как единое» (основатель теории множеств – Георг Кантор). КАНТОР (Cantor) Георг (1845—1918) — немецкий математик, логик, теолог, создатель теории трансфинитных (бесконечных) множеств, оказавшей определяющее влияние на развитие математических наук на рубеже 19— 20 вв.
Множество — одно из основных понятий современной математики, используемое почти во всех её разделах.
К сожалению, основному понятию теории – понятию множества – нельзя дать строгого определения. Разумеется, можно сказать, что множество – это «совокупность», «собрание», «ансамбль», «коллекция», «семейство», «система», «класс» и т. д. однако всё это было бы не математическим определением, а скорее злоупотреблением словарным богатством русского языка.
Разумеется, можно сказать, что множество – это «совокупность», «собрание», «ансамбль», «коллекция», «семейство», «система», «класс» и т. д. однако всё это было бы не математическим определением, а скорее злоупотреблением словарным богатством русского языка.
Для того чтобы определить какое – либо понятие, нужно, прежде всего, указать, частным случаем какого более общего понятия, оно является, для понятия множества сделать это невозможно, потому что более общего понятия, чем множество, в математике нет.
Часто приходится говорить о нескольких вещах, объединенных некоторым признаком. Так, можно говорить о множестве всех стульев в комнате, о множестве всех клеток человеческого тела, о множестве всех картофелин в данном мешке, о множестве всех рыб в океане, о множестве всех квадратов на плоскости, о множестве всех точек на данной окружности т. д.
Предметы, составляющие данное множество, называются его элементами.
Например, множество дней недели состоит из элементов: понедельник, вторник, среда, четверг, пятница, суббота, воскресенье.
Множество месяцев – из элементов: январь, февраль, март, апрель, май, июнь, июль, август, сентябрь, октябрь, ноябрь, декабрь.
Множество арифметических действий — из элементов: сложение, вычитание, умножение, деление.
Например, если А означает множество всех натуральных чисел, то 6 принадлежит к А, а 3 не принадлежит к А.
Если А — множество всех месяцев в году, то май принадлежит к А, а среда не принадлежит к А.
Если множество содержит конечное число элементов, то его называют конечным, а если в нем бесконечно много элементов, то бесконечным. Так множество деревьев в лесу конечно, а множество точек на окружности бесконечно.
Парадокс в логике — это противоречие, имеющее статус логически корректного вывода и, вместе с тем, представляющее собой рассуждение, приводящее к взаимно исключающим заключениям.
Как уже упоминалось, понятие множества лежит в основе математики. Используя простейшие множества и различные математические конструкции, можно построить практически любой математический объект.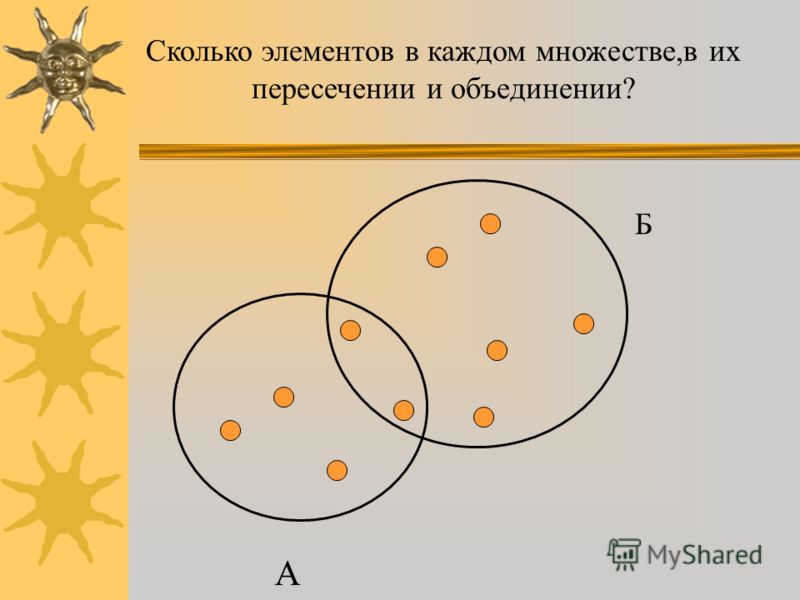 Идею построения всей математики на основе теории множеств активно пропагандировал Г.Кантор. Однако, при всей своей простоте, понятие множества таит в себе опасность появления противоречий или, как ещё говорят, парадоксов. Появление парадоксов связано с тем, что далеко не всякие конструкции и не всякие множества можно рассматривать.
Идею построения всей математики на основе теории множеств активно пропагандировал Г.Кантор. Однако, при всей своей простоте, понятие множества таит в себе опасность появления противоречий или, как ещё говорят, парадоксов. Появление парадоксов связано с тем, что далеко не всякие конструкции и не всякие множества можно рассматривать.
Самый простой из парадоксов — это «парадокс брадобрея«.
Одному солдату было приказано брить тех и только тех солдат его взвода, которые сами себя не бреют. Неисполнение приказа в армии, как известно, тягчайшее преступление. Однако возник вопрос, брить ли этому солдату самого себя. Если он побреется, то его следует отнести к множеству солдат, которые сами себя бреют, а таких брить он не имеет права. Если же он себя брить не будет, то попадёт во множество солдат, которые сами себя не бреют, а таких солдат согласно приказу он обязан брить. Парадокс.
Над множествами, как и над многими другими математическими объектами, можно совершать различные операции, которые иногда называют теоретико-множественными операциями или сет-операциями. В результате операций из исходных множеств получаются новые. Множества обозначаются заглавными латинскими буквами, а их элементы – строчными. Запись aR означает, что элемент а принадлежит множеству R , то есть а является элементом множества R . В противном случае, когда а не принадлежит множеству R , пишут aR .
В результате операций из исходных множеств получаются новые. Множества обозначаются заглавными латинскими буквами, а их элементы – строчными. Запись aR означает, что элемент а принадлежит множеству R , то есть а является элементом множества R . В противном случае, когда а не принадлежит множеству R , пишут aR .
Два множества А и В называются равными ( А = В ), если они состоят из одних и тех же элементов, то есть каждый элемент множества А является элементом множества В и наоборот, каждый элемент множества В является элементом множества А .
Сравнение множеств.
Множество A содержится во множестве B (множество B включает множество A), если каждый элемент A есть элемент В:
Говорят, что множество А содержится в множестве В или множество Аявляется подмножеством множества В ( в этом случае пишут А В ), если каждый элемент множества А одновременно является элементом множества В . Эта зависимость между множествами называется включением. Для любого множества А имеют место включения: ØА и А А
Эта зависимость между множествами называется включением. Для любого множества А имеют место включения: ØА и А А
В этом случае A называется подмножеством B, B — надмножеством A. Если , то A называется собственным подмножеством В. Заметим, что ,
По определению ,
Два множества называются равными, если они являются подмножествами друг друга
Операции над множествами
Пересечение.
Объединение.
Свойства.
1.Операция объединения множеств коммутативна
2.Операция объединения множеств транзитивна
3. Пустое множество X является нейтральным элементом операции объединения множеств
Примеры:
1. Пусть A = {1,2,3,4},B = {3,4,5,6,7}. Тогда
Пусть A = {1,2,3,4},B = {3,4,5,6,7}. Тогда
2. А={2,4,6,8,10}, В = {3,6,9,12}. Найдём объединение и пересечение этих множеств:
{2,4,6,8, 10,3,6,9,12}, = {6}.
3. Множество детей является подмножеством всего населения
4. Пересечением множества целых чисел с множеством положительных чисел является множество натуральных чисел.
5. Объединением множества рациональных чисел с множеством иррациональных чисел является множество положительных чисел.
6.Нуль является дополнением множества натуральных чисел относительно множества неотрицательных целых чисел.
Диаграммы Венна (Venn diagrams) — общее название целого ряда методов визуализации и способов графической иллюстрации, широко используемых в различных областях науки и математики: теория множеств, собственно «диаграмма Венна» показывает все возможные отношения между множествами или событиями из некоторого семейства; разновидностями диаграмм Венна служат: диаграммы Эйлера,
Диаграмма Венна четырёх множеств.
Собственно «диаграмма Венна» показывает все возможные отношения между множествами или событиями из некоторого семейства. Обычная диаграмма Венна имеет три множества. Сам Венн пытался найти изящный способ с симметричными фигурами, представляющий на диаграмме большее число множеств, но он смог это сделать только для четырех множеств (см. рисунок справа), используя эллипсы.
Диаграммы Эйлера
Диаграммы Эйлера аналогичны диаграммам Венна.Диаграммы Эйлера можно использовать, для того, чтобы оценивать правдоподобность теоретико-множественных тождеств.
Задача 1. В классе 30 человек, каждый из которых поёт или танцует. Известно, что поют 17 человек, а танцевать умеют 19 человек. Сколько человек поёт и танцует одновременно?
Решение: Сначала заметим, что из 30 человек не умеют петь 30 — 17 = 13 человек.
Все они умеют танцевать, т. к. по условию каждый ученик класса поёт или танцует. Всего умеют танцевать 19 человек, из них 13 не умеют петь, значит, танцевать и петь одновременно умеют 19-13 = 6 человек.
к. по условию каждый ученик класса поёт или танцует. Всего умеют танцевать 19 человек, из них 13 не умеют петь, значит, танцевать и петь одновременно умеют 19-13 = 6 человек.
Задачи на пересечение и объединение множеств.
- Даны множества А = {3,5, 0, 11, 12, 19}, В = {2,4, 8, 12, 18,0}.
Найдите множества AU В, - Составьте не менее семи слов, буквы которых образуют подмножества множества
А -{к,а,р,у,с,е,л,ь}. - Пусть A — это множество натуральных чисел, делящихся на 2, а В — множество натуральных чисел, делящихся на 4. Какой вывод можно сделать относительно данных множеств?
- На фирме работают 67 человек. Из них 47 знают английский язык, 35 — немецкий язык, а 23 — оба языка. Сколько человек фирмы не знают ни английского, ни немецкого языков?
- Из 40 учащихся нашего класса 32 любят молоко, 21 — лимонад, а 15 — и молоко, и лимонад. Сколько ребят в нашем классе не любят ни молоко, ни лимонад?
- 12 моих одноклассников любят читать детективы, 18 -фантастику, трое с удовольствием читают и то, и другое, а один вообще ничего не читает.
 Сколько учеников в нашем классе?
Сколько учеников в нашем классе? - Из тех 18 моих одноклассников, которые любят смотреть триллеры, только 12 не прочь посмотреть и мультфильмы. Сколько моих одноклассников смотрят одни «мультики», если всего в нашем классе 25 учеников, каждый из которых любит смотреть или триллеры, или мультфильмы, или и то и другое?
- Из 29 мальчишек нашего двора только двое не занимаются спортом, а остальные посещают футбольную или теннисную секции, а то и обе. Футболом занимается 17 мальчишек, а теннисом — 19. Сколько футболистов играет в теннис? Сколько теннисистов играет в футбол?
- 65 % бабушкиных кроликов любят морковку, 10 % любят и морковку, и капусту. Сколько процентов кроликов не прочь полакомиться капустой?
- В одном классе 25 учеников. Из них 7 любят груши, 11 -черешню. Двое любят груши и черешню; 6 — груши и яблоки; 5 -яблоки и черешню. Но есть в классе два ученика, которые любят все и четверо таких, что не любят фруктов вообще.
 Сколько учеников этого класса любят яблоки?
Сколько учеников этого класса любят яблоки? - В конкурсе красоты участвовали 22 девушки. Из них 10 было красивых, 12 -умных и 9 -добрых. Только 2 девушки были и красивыми, и умными; 6 девушек были умными и одновременно добрыми. Определите, сколько было красивых и в то же время добрых девушек, если я скажу вам, что среди участниц не оказалось ни одной умной, доброй и вместе с тем красивой девушки?
- В нашем классе 35 учеников. За первую четверть пятерки по русскому языку имели 14 учеников; по математике — 12; по истории — 23. По русскому и математике — 4; по математике и истории — 9; по русскому языку и истории — 5. Сколько учеников имеют пятерки по всем трем предметам, если в классе нет ни одного ученика, не имеющего пятерки хотя бы по одному из этих предметов?
- Из 100 человек 85 знают английский язык, 80 — испанский, 75 — немецкий. Все владеют, по крайней мере, одним иностранным языком. Среди них нет таких, которые знают два иностранных языка, но есть владеющие тремя языками.
 Сколько человек из этих 100 знают три языка?
Сколько человек из этих 100 знают три языка? - Из сотрудников фирмы 16 побывали во Франции, 10 -в Италии, 6 — в Англии; в Англии и Италии — 5; в Англии и Франции — 6; во всех трех странах — 5 сотрудников. Сколько человек посетили и Италию, и Францию, если всего в фирме работают 19 человек, и каждый из них побывал хотя бы в одной из названных стран?
- Мне больше всего удалось…
- Для меня было открытием то, что …
- За что ты можешь себя похвалить?
- Что на ваш взгляд не удалось? Почему? Что учесть на будущее?
- Мои достижения на уроке.
- Макарычев. Пункт 13. №263, №264, №265, №266, № 271, №272.
- Составить задачи на применение теории множеств.
- По группам подготовить презентации по теме « Множества».

«Пересечение и объединение множеств» презентация к уроку по математике (3 класс) на тему. Какое из утверждений неверно
- Множество натуральных чисел – это…
- Множество учащихся 8 класса – это…
- Множество не положительных и неотрицательных чисел – это…
1.Пересечение множеств
А={1,2,3,4,6,8,12,24},
В={1,2,3,6,9,18},
С- множество общих делителей чисел 24 и 18,
Говорят, что множество С является пересечением множеств А и В.
- Множество, составляющее общую часть множеств А и В, называют пересечением этих множеств и обозначают так: А∩В=С.
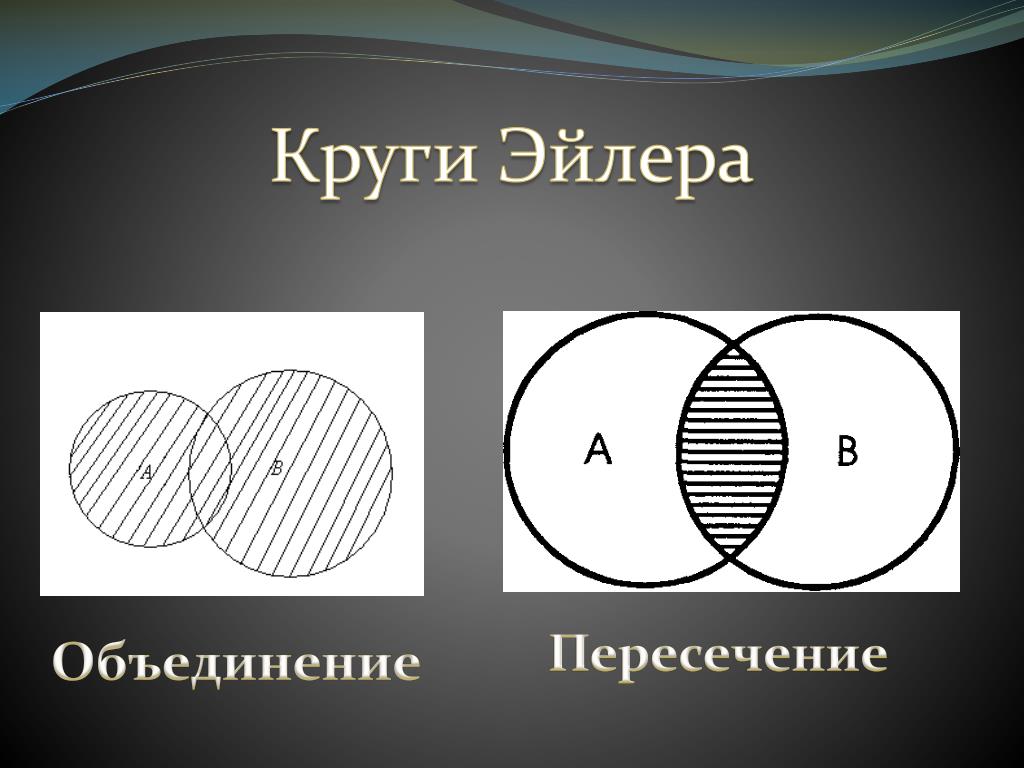
- Соотношение между множествами А,В и С можно проиллюстрировать с помощью специальных схем, называемых кругами Эйлера.
Фигура, образовавшаяся при пересечении кругов, закрашенная на рисунке, изображает множество С.
Замечание.
Некоторые множества Х и Y не имеют общих элементов. Тогда говорят, что пересечением множеств Х и Y является пустое множество.
Ø — обозначение пустого множества.
И пишут тогда так: Х∩ Y = Ø
Например:
2.Объединение множеств
А- множество натуральных делителей числа 24,
В- множество натуральных делителей числа 18.
А={1,2,3,4,6,8,12,24},
В={1,2,3,6,9,18},
D- множество, которому принадлежат все элементы множества А и все элементы множества В.
Т.е. D ={1,2,3,4,6,8,9,12,18,24}.
Говорят, что множество D является объединением множеств А и В.
Множества А и В изображены на рисунке кругами.
Фигура, закрашенная на рисунке, является объединением множеств А и В.
Например:
Х-множество простых чисел, не превосходящих 25;
Y- множество двузначных чисел, не превосходящих 19.
Найдите пересечение и объединение множеств Х и Y .
X={2, 3, 5, 7, 11, 13, 17, 19, 23};
Y={10,11,12,13,14,15,16,17,18};
Общие элементы: 11,13,17, значит,
X∩ Y ={11,13,17};
X UY ={2, 3, 5, 7,10,11,12,13,14,15, 16,17,18,19,23}.
- Решить в классе
- № 799
- Решить дома
- № 800
Множества. Операции над множествами
МНОЖЕСТВО
НАХОДИТЬ ОБЪЕДИНЕНИЕ МНОЖЕСТВ
ЭЛЕМЕНТ МНОЖЕСТВА
ВИДЫ МНОЖЕСТВ
НАХОДИТЬ ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ
ОТНОШЕНИЯ МЕЖДУ
МНОЖЕСТВАМИ
ИЗОБРАЖАТЬ С ПОМОЩЬЮ КРУГОВ ЭЙЛЕРА
«Множество есть многое, мыслимое нами как единое»
основатель теории множеств
Георг Кантор
Понятия теории множеств
Понятие множества является одним из наиболее общих и наиболее важных математических понятий. Оно было введено в математику немецким ученым Георгом Кантором (1845-1918).Следуя Кантору, понятие «множество» можно определить так:
- Множество- совокупность объектов, обладающих определенным свойством, объединенных в единое целое.
НАБОР КАРАНДАШЕЙ
КОЛЛЕКЦИЯ МАРОК
СТАЯ ПТИЦ
СТАДО КОРОВ
ЧАЙНЫЙ СЕРВИЗ
БУКЕТ ЦВЕТОВ
Множество – совокупность объектов, объединенных по какому–нибудь признаку.
Множества обозначают большими буквами латинского алфавита: А, В, С, D и т. д.
Объекты, составляющие множество, называются элементами множества.
множество
элемент
Трапеция, параллелограмм, ромб, квадрат, прямоугольник
Шар, прямоугольный параллелепипед, призма, пирамида, октаэдр
Натуральные числа
1, 4, 9, 16, 25, 36, 49, 64, 81, 100 ..
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Двузначные четные числа
Множество четырехугольников
Пространственные тела
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11…
Квадраты чисел
Цифры десятичной системы счисления
10, 12, 14, 16 … 96, 98
множество людей на Солнце
множество прямых углов равностороннего треугольника
множество точек пересечения двух параллельных прямых
Пустое множество- множество, не содержащее ни одного элемента.
Обозначения некоторых числовых множеств:
N – множество натуральных чисел;
Z – множество целых чисел;
Q – множество рациональных чисел;
I — множество иррациональных чисел;
R – множество действительных чисел.
ВИДЫ МНОЖЕСТВ
Запишите множества букв слов
КОНИ И КИНО
{ К, О, Н, И }
{ К, И, Н, О }
Равные множества
ВИДЫ МНОЖЕСТВ
А = {2; 3; 5; 7; 11; 13};
Конечные множества
ВИДЫ МНОЖЕСТВ
{1; 4; 9; 16; 25; …};
{10; 20; 30; 40; 50; …};
Бесконечные множества
Среди перечисленных ниже множеств укажите конечные и бесконечные множества:
а) множество чисел, кратных 13;
б) множество делителей числа 15;
в) множество деревьев в лесу;
г) множество натуральных чисел;
д) множество рек Ростовской области;
е) множество корней уравнения х + 3 = 11;
ж) множество решений неравенства х + 1
Задайте множество цифр, с помощью которых записывается число:
а) 3254; б) 8797; в) 11000; г) 555555.
Охарактеризуйте множество А:
а) А = {1, 3, 5, 7, 9};
б) А = {- 2, — 1, 0, 1, 2};
в) А = {11, 22, 33, 44, 55, 66, 77, 88, 99};
Даны множества:
М = {5, 4, 6},
Р = {4, 5, 6},
Т = {5, 6, 7},
S = {4, 6}.
Какое из утверждений неверно?
а) М = Р б) Р ≠ S в) М ≠ Т г) Р = Т
Пусть А — множество простых чисел вида
7n + 2, где n ∈ N.
Верна ли запись -5 ∈ А.
1. В множестве {лев; лисица; гиена; слон; рысь} все элементы, кроме одного, обладают некоторым свойством. а) опишите это свойство; б) найдите элемент, не обладающий этим свойством; в) назовите еще два элемента, обладающие этим свойством. 2. Назовите 5 подмножеств в множестве всех цветов радуги. 3. Каким свойством в множестве ромбов выделяется подмножество квадратов?
Пример: 8 и 32
БЛИЦ-ОПРОС
- земноводные, млекопитающие, хладнокровные и т.п.
Какие названия применяются для обозначения множеств животных?
БЛИЦ-ОПРОС
- рота, взвод, полк, дивизия и т.
 п.
п.
Какие названия применяются для обозначения множеств военно-служащих?
БЛИЦ-ОПРОС
Как называется множество цветов, стоящих в вазе?
БЛИЦ-ОПРОС
Как называется множество точек земной поверхности, равноудаленных от обоих полюсов?
БЛИЦ-ОПРОС
- деревня, село, город, посёлок
Как называется множество населённых людьми мест?
БЛИЦ-ОПРОС
- выставка, галерея
Как называется множество картин?
БЛИЦ-ОПРОС
Как называется множество документов?
БЛИЦ-ОПРОС
- флотилия, эскадра
Какие названия применяют для обозначения множеств кораблей?
А – четные натуральные числа В – двузначные числа
Найти объединение этих множеств.
А В – быть четным натуральным или двузначным числом
Пример: 8 и 32
А – четные натуральные числа В – двузначные числа
Найти пересечение этих множеств.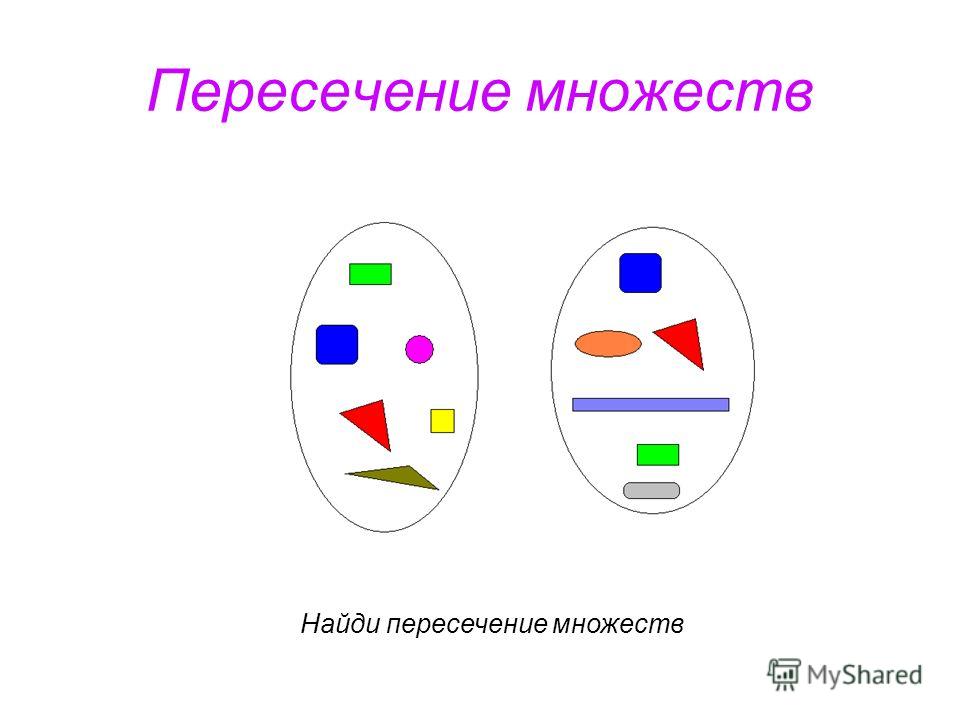
А В – быть четным натуральным и двузначным числом
Пример: 32
Даны множества:
А = {2; 3; 8},
В = {2; 3; 8; 11},
С = {5; 11}.
Найдите: 1) АUВ; 2) АUС; 3) СUВ.
Даны множества:
А = { a , b , c , d },
B = { c , d , e , f },
C = { c , e , g , k }.
Найдите: (АUВ)UС.
Даны множества:
А – множество всех натуральных чисел, кратных 10,
В = {1; 2; 3;…, 41}.
Найдите А∩В.
Решение задачи
с помощью кругов Эйлера
Леона́рд Э́йлер — швейцарский, немецкий и российский математик, внёсший значительный вклад в развитие математики, а также механики, физики, астрономии и ряда прикладных наук.
В классе 30 человек, каждый из которых поёт или танцует. Известно, что поют 17 человек, а танцевать умеют 19 человек. Сколько человек поёт и танцует одновременно?
танцуют 19
17+19=36, всего 30
Решение
Пусть А — это множество учеников, умеющих петь. Количество элементов в нём по условию равно n = 17. Пусть В — множество учеников, умеющих танцевать. Количество элементов в нём — m = 18. Множество совпадает со всем классом, т.к. каждый ученик в классе поёт или танцует. — это множество тех учеников класса, которые поют и танцуют одновременно. Пусть их количество равно k .
Согласно формуле доказанной выше
n + m- k = 17+ 19- k = 30 k = 6.
Ответ: 6 учеников в классе поют и танцуют одновременно.
На фирме работают 67 человек. Из них 47 знают английский язык, 35 — немецкий язык, а 23 — оба языка. Сколько человек в фирме не знают ни английского, ни немецкого языков?
Немецкий 35
Английский 47
Каждый учащийся в классе изучает английский или французский язык. Английский язык изучают 25 учащихся, французский — 27 учащихся, а два языка — 18 учащихся. Сколько учащихся в классе?
Английский язык изучают 25 учащихся, французский — 27 учащихся, а два языка — 18 учащихся. Сколько учащихся в классе?
Немецкий 27
Английский 25
Только немецкий
Только английский
Ответ: в классе 34 ученика
Множества А и В содержат соответственно 5 и 6 элементов, а множество А ∩ В – 2 элемента. Сколько элементов в множестве А U В?
Объединение содержит 9 элементов
Каждая семья, живущая в нашем доме, выписывает или
газету, или журнал, или и то и другое вместе. 75 семей
выписывают газету, а 27 семей выписывают журнал и лишь 13 семей выписывают и журнал, и газету. Сколько семей живет в нашем доме?
Всего: 14 + 13 + 62 =89
На школьной спартакиаде каждый из 25 учеников 9 –го
класса выполнил норматив или по бегу, или по прыжкам в высоту. Оба норматива выполнили 7 человек, а 11 учеников выполнили норматив по бегу, но не выполнили норматив по прыжкам в высоту.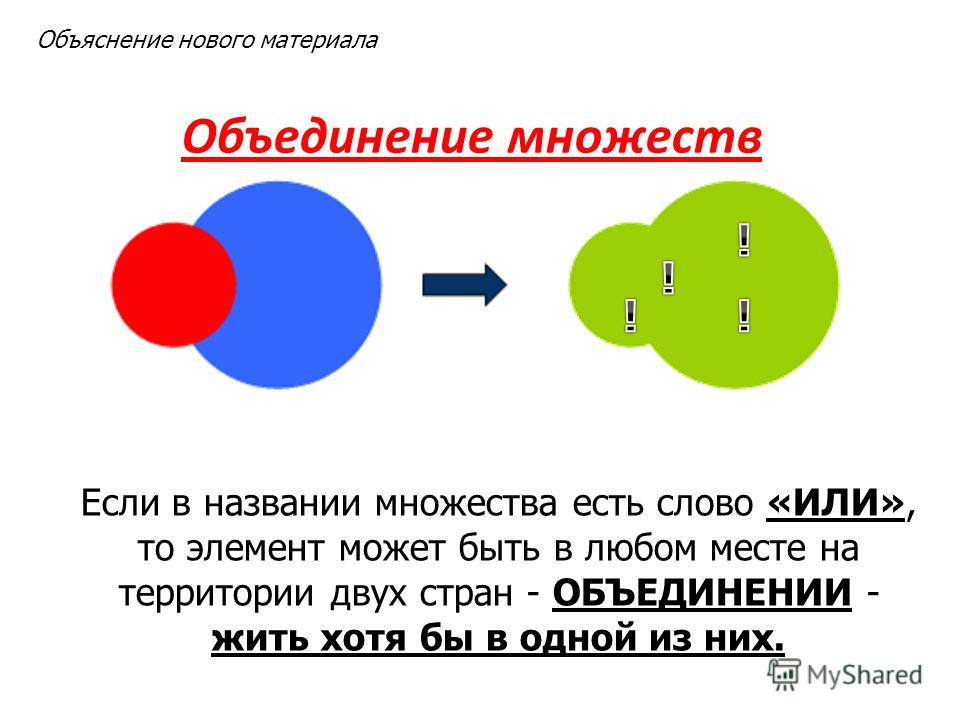 Сколько учеников выполнили норматив: а) по бегу; б) по прыжкам в высоту; в) по прыжкам при условии, что не выполнен норматив по бегу?
Сколько учеников выполнили норматив: а) по бегу; б) по прыжкам в высоту; в) по прыжкам при условии, что не выполнен норматив по бегу?
В воскресенье 19 учеников нашего класса побывали в
планетарии, 10 – в цирке и 6 – на стадионе. Планетарий и цирк посетили 5 учеников; планетарий и стадион — 3; цирк и стадион — 1. Сколько учеников в нашем классе, если никто не успел посетить все три места, а три ученика не посетили ни одного места?
МНОЖЕСТВО
НАХОДИТЬ ОБЪЕДИНЕНИЕ МНОЖЕСТВ
ЭЛЕМЕНТ МНОЖЕСТВА
ВИДЫ МНОЖЕСТВ
НАХОДИТЬ ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ
ОТНОШЕНИЯ МЕЖДУ
МНОЖЕСТВАМИ
ИЗОБРАЖАТЬ С ПОМОЩЬЮ КРУГОВ ЭЙЛЕРА-ВЕННА
РЕШАТЬ ЗАДАЧИ С ИСПОЛЬЗОВАНИЕМ ИМЕЮЩИХСЯ ЗНАНИЙ
Сенина Г.Н., Сенин В.Г., МБОУ «СОШ №4», г.Корсаков
МНОЖЕСТВА. КОМБИНАТОРИКА.
ПЕРЕСЕЧЕНИЕ И ОБЪЕДИНЕНИЕ МНОЖЕСТВ.
Метапредмет – Знание
Цель нашего урока
В рассказе Конан Дойля «Пять апельсиновых зернышек» знаменитый сыщик Шерлок Холмс должен был установить название одного парусника. Об этом судне он знал лишь то, что в январе 1883 г. Оно было в Пондишире, в январе 1885 г. – в Данди, а сейчас стояло в Лондоне. Сравнив списки парусников, находившихся в указанное время в указанных местах, Шерлок Холмс установил, что только американское судно «Одинокая звезда» входило в каждый из них. В результате преступление было раскрыто. Сыщик, имея три множества, построил новое, содержащее их общие элементы. Оказалось, что новое множество состоит всего из одного элемента
Об этом судне он знал лишь то, что в январе 1883 г. Оно было в Пондишире, в январе 1885 г. – в Данди, а сейчас стояло в Лондоне. Сравнив списки парусников, находившихся в указанное время в указанных местах, Шерлок Холмс установил, что только американское судно «Одинокая звезда» входило в каждый из них. В результате преступление было раскрыто. Сыщик, имея три множества, построил новое, содержащее их общие элементы. Оказалось, что новое множество состоит всего из одного элемента
целеполагание
Проверим домашнее задание
УЧЕБНИК
№ 747
УЧЕБНИК
№ 749
P ⊂ N ⊂ Z ; C ⊂ B ⊂ A; K ⊂ P ⊂ R
Вхождение в тему урока и создание условий для осознанного восприятия нового материала.
Пересечение и объединение множеств
Организация и самоорганизация учащихся. Организация обратной связи
Работаем с текстом
ТРЕНАЖЕР
№ 319
в каждое из данных множеств
Практикум
Работаем с текстом
ТРЕНАЖЕР
№ 320
Практикум
Работаем с моделями
ТРЕНАЖЕР
№ 323
Практикум
Работаем с моделями
ТРЕНАЖЕР
№ 324
Практикум
Операции над множествами
ЗАДАЧНИК
№ 638
ЗАДАЧНИК
№ 639
Практикум
Операции над множествами
ЗАДАЧНИК
№ 641
{-1,0,1}; {-5,-4,-3,-2,-1,0,1,2}
{-1,0}; {-4,-3,-2,-1,0,1}
{1}; {-2,-1,0,1,2,3,4}
{-1,0,1}; {-2,-1,0,1,2}
Практикум
Операции над множествами
УЧЕБНИК
№ 757
Свойства нуля при умножении и сложении чисел: А ⋅ 0 = 0; А + 0 = А.
Практикум
Операции над множествами
УЧЕБНИК
№ 758
Операции над множествами
№ 760
УЧЕБНИК
Проверка полученных результатов. Коррекция
Множества и жизнь
Множество – это фундаментальное понятие не только математики, но и всего окружающего мира.
Возьмите прямо сейчас в руку любой предмет. Вот вам и множество, состоящее из одного элемента.
Возьмите большой пакет и начните наобум складывать в него различные предметы.
В этом нет никакой закономерности, но, тем не менее, речь идёт о множестве предметов.
Домашнее задание У: стр. 228 – 229, фрагмент 1 – читать;
№ 751, 752, 756, 759.
Подведение итогов, рефлексия, домашнее задание.
Презентация по теме «Пересечение и объединение множеств» (факультатив «Наглядная геометрия» (3 класс).
Использование информационных технологий не только оживило учебный процесс (что особенно важно, если учитывать психологические особенности младшего школьного возраста, в частности длительное преобладание наглядно-образного мышления над абстрактно-логическим), но и повысило мотивацию обучения на занятии.
Скачать:
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Пересечение и объединение множеств. Кунделева Оксана Евгеньевна Учитель начальных классов МБОУ НОШ № 279 г. Гаджиево, Мурманской области, 2012 г.
Цели занятия формировать представление об объединении и пересечении двух множеств учить находить на «карте множеств» область множества, которое является пересечением или объединением двух множеств учить определять принадлежность элементов множеству, которое является пересечением и объединением двух множеств учить определять характер отношений между двумя заданными множествами (пересечение, не пересекаются, объединение)
Что такое множество? Множество — это группа предметов, объектов или существ.
Назовите элементы множества: “Месяцы года” “Времена года” “Материки” “Летающие бегемоты” Многоугольники
Оса Летучая мышь ворона пингвин Бабочка синица страус воробей Прочитайте названия птиц. Обведите это множество. Сделайте надпись внизу: “Птицы”. ПТИЦЫ Прочитайте названия животных, которые умеют летать. Обведите это множество, сделайте надпись вверху: ”Умеют летать”. умеют летать Сколько элементов оказалось на пересечении двух множеств, т.е. одновременно в двух множествах? Почему?
Обведите это множество. Сделайте надпись внизу: “Птицы”. ПТИЦЫ Прочитайте названия животных, которые умеют летать. Обведите это множество, сделайте надпись вверху: ”Умеют летать”. умеют летать Сколько элементов оказалось на пересечении двух множеств, т.е. одновременно в двух множествах? Почему?
Пересечение множеств общая часть множеств Если в названии множества есть слово «И» , то каждый его элемент должен находиться на ПЕРЕСЕЧЕНИИ двух множеств – жить одновременно в двух странах. !
Объединение множеств Если в названии множества есть слово «ИЛИ» , то элемент может быть в любом месте на территории двух стран — ОБЪЕДИНЕНИИ — жить хотя бы в одной из них. ! ! ! !
Что такое подмножество? Подмножество – это часть множества, входящее в данное множество.
Физкультминутка Раз – согнуться, разогнуться, Два – нагнуться, потянуться, Три – в ладоши три хлопка, Головою три кивка. На четыре руки шире, Пять, шесть – тихо сесть, Семь, восемь – лень отбросим.
Множество обитателей моря Множество млекопитающих Начерти множества:
Начерти множества: Множество птиц Множество рыб
В квадрате живут чётные числа. В треугольнике живут двузначные числа. Впиши правильно каждое число. Закрась на рисунке область, где живут чётные двузначные числа. 2, 47, 16, 8, 17, 32, 6, 53 2 47 16 8 17 32 53 6
В треугольнике живут двузначные числа. Впиши правильно каждое число. Закрась на рисунке область, где живут чётные двузначные числа. 2, 47, 16, 8, 17, 32, 6, 53 2 47 16 8 17 32 53 6
Найди обозначение каждого множества в таблице и закрась круги на рисунке. Множества: прямоугольников четырёхугольников многоугольников квадратов Сколько множеств обозначено кругами? Какое множество самое большое? Каким цветом нужно закрасить самый большой круг? Какое самое большое из оставшихся?
Множества: животных Зверей Рыб Птиц Растений Чайка Лиса Айсберг Жираф Сосна Река Тюльпан Муравей Камбала Найди и расположи элементы множеств в фигурах на рисунке: впиши первую букву каждого слова из списка
Ч К М Т Р С Ж А Л
Запомни! Множества не пересекаются Множества не пересекаются: Одно множество является подмножеством другого Одно множество является подмножеством другого: Множества пересекаются: Множества объединяются:
До встречи на следующем уроке!!!
А.В. Горячев, К.И. Горина и др. Информатика в играх и задачах, 3 класс, Методические рекомендации для учителя, М., « Баллас », 2004 А.В. Горячев, К.И. Горина и др. Учебник «Информатика в играх и задачах», 3 класс, часть 2, М., « Баллас », 2004 http://festival.1september.ru/articles/505635/ Урок информатики по теме «Множество. Подмножество. Пересечение множеств» Щепина Зинаида Николаевна, учитель начальных классов Используемая литература
Информатика в играх и задачах, 3 класс, Методические рекомендации для учителя, М., « Баллас », 2004 А.В. Горячев, К.И. Горина и др. Учебник «Информатика в играх и задачах», 3 класс, часть 2, М., « Баллас », 2004 http://festival.1september.ru/articles/505635/ Урок информатики по теме «Множество. Подмножество. Пересечение множеств» Щепина Зинаида Николаевна, учитель начальных классов Используемая литература
Пересечение и объединение множеств.
Кунделева Оксана Евгеньевна
Учитель начальных классов МБОУ НОШ №279 г. Гаджиево, Мурманской области,
Цели занятия
- формировать представление об объединении и пересечении двух множеств
- учить находить на «карте множеств» область множества, которое является пересечением или объединением двух множеств
- учить определять принадлежность элементов множеству, которое является пересечением и объединением двух множеств
- учить определять характер отношений между двумя заданными множествами (пересечение, не пересекаются, объединение)
 Назовите элементы множества:
Назовите элементы множества:- “Месяцы года”
- “Времена года”
- “Материки”
- “Летающие бегемоты”
- Многоугольники
Летучая мышь ворона пингвин
Бабочка синица страус
Прочитайте названия птиц. Обведите это множество. Сделайте надпись внизу: “Птицы”.
Прочитайте названия животных, которые умеют летать. Обведите это множество, сделайте надпись вверху: ”Умеют летать”.
умеют летать
Сколько элементов оказалось на пересечении двух множеств , т.е. одновременно в двух множествах? Почему?
Пересечение множеств общая часть множеств«И» ,
то каждый его элемент должен находиться на ПЕРЕСЕЧЕНИИ двух множеств –
жить одновременно в двух странах .
Объединение множествЕсли в названии множества есть слово «ИЛИ» ,
то элемент может быть в любом месте на территории двух стран — ОБЪЕДИНЕНИИ —
жить хотя бы в одной из них.
Множество обитателей моря
Множество млекопитающих
Начерти множества:
Множество птиц
Множество рыб
В квадрате живут чётные числа. В треугольнике живут двузначные числа. Впиши правильно каждое число. Закрась на рисунке область, где живут чётные двузначные числа.
2, 47, 16, 8, 17, 32, 6, 53
Найди обозначение каждого множества в таблице и закрась круги на рисунке.
Сколько множеств обозначено кругами? Какое множество самое большое? Каким цветом нужно закрасить самый большой круг? Какое самое большое из оставшихся?
Множества:
животных
Растений
Найди и расположи элементы множеств в фигурах на рисунке: впиши первую букву каждого слова из списка
Запомни!
- Множества не пересекаются
Множества не пересекаются:
- Одно множество является подмножеством другого
Одно множество является подмножеством другого:
Множества пересекаются:
Множества объединяются:
До встречи на
следующем уроке!!!
А.В. Горячев, К.И. Горина и др. Информатика в играх и задачах, 3 класс, Методические рекомендации для учителя, М., «Баллас», 2004
- А.В. Горячев, К.И. Горина и др. Информатика в играх и задачах, 3 класс, Методические рекомендации для учителя, М., «Баллас», 2004
- А.В. Горячев, К.И. Горина и др. Учебник «Информатика в играх и задачах», 3 класс, часть 2, М., «Баллас», 2004
- http://festival.1september.ru/articles/505635/ Урок информатики по теме «Множество. Подмножество. Пересечение множеств» Щепина Зинаида Николаевна, учитель начальных классов
Используемая литература
Что такое пересечение, объединение и разность множеств?
☰
Пересечением двух множеств, называется третье множество, сформированное из элементов, которые входят в оба первых множества.
Например, если в одно множество входят числа от 1 до 10, а во второе — от 5 до 20, то пересечением этих множеств будут числа от 5 до 10, так как они входят в оба.
Пересечение множеств записывается так:
A ∩ B = {x | x ∈ A и x ∈ B}
На диаграмме Эйлера-Венна пересечение множеств обозначается общей частью кругов.
Множества могут не пересекаться вообще, одно может полностью включать другое.
Пересечение множеств может использоваться тогда, когда надо найти элементы, которые удовлетворяют нескольким условиям.
Объединением двух множеств, называется третье множество, сформированное из всех элементов обоих первых множеств. При этом если элемент входит в оба множества, то в объединенное он входит один раз. Это и понятно, так как множество по определению включает только разные элементы.
Например, объединением множества натуральных чисел от 1 до 10 и множества натуральных от 5 до 15 будет множество натуральных чисел от 1 до 15.
Объединение множеств описывается так:
A ∪ B = {x | x ∈ A или x ∈ B}
На диаграмме Эйлера-Венна объединение множеств обозначается всей областью кругов.
Разностью двух множеств, называют третье множество, в которое входят все элементы одного из двух множеств и не входят элементы принадлежащие обоим множествам.
Если результат пересечения и объединения двух множеств не меняется от перестановки множеств при выполнении операции, то результат разности зависит от того, какое множество из какого «вычитают».
Сравните. Даны множества A = {1,2,3,4,5} и B = {4,5,8,9}. Разность множеств обозначается знаком \.
A \ B = {1,2,3}, т. к. 4 и 5 входят в множество B.
В то время как B \ A = {8,9}.
Понятно, что если у множеств нет общих элементов, то их разность будет равна «уменьшаемому», т. е. первому множеству. Если же множества полностью совпадают, то их разностью будет пустое множество.
Если все элементы «вычитаемого» множества B входят в состав «уменьшаемого» A (A \ B), то B называют дополнением некого множества C до A.
свойства, формулы включений и исключений, примеры
Пересечение множеств
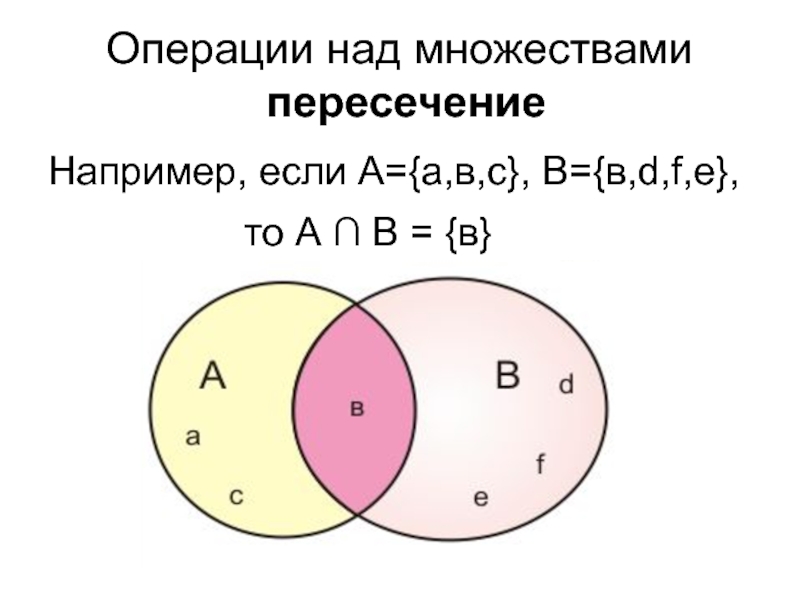
Пересечением множеств A и B называют множество, содержащее те и только те элементы, которые входят одновременно как в множество A, так и в множество B:
$$ A \cap B = \{x|x \in \Bbb A и x \in \Bbb B \} $$
Если множества не пересекаются, то $A \cap B = \varnothing $ — пустое множество в пересечении. Если $B \subseteq A$ — подмножество, то $A \cap B = B$ – пересечением будет меньшее множество из двух.
Например:
Если A = {1;3;5;9}, Β = {3;7;11}, то $A \cap B$ = {3;5}.
Если A = {f|f-прямоугольник}, B = {f|f-ромб}, то $A \cap B$ = {f|f-квадрат}.
Если A = $\{n|n⋮3, n \in \Bbb N \}$ — натуральные числа, кратные 3, B = $\{n|n⋮5, n \in \Bbb N \}$ — натуральные числа, кратные 5, то $A \cap B = {n|n⋮15, n \in \Bbb N}$ — натуральные числа, кратные 15.
Если A = {a│a-слон}, B = {a|a-птица}, то $A \cap B = \varnothing$.
Объединение множеств
Объединением – множеств A и B называют множество, содержащее те и только те элементы, которые входят хотя бы в одно из множеств, A или B:
$$ A \cup B = \{ x|x \in \Bbb A или x \in \Bbb B \} $$
Если $B \subseteq A$ — подмножество, то $A \cap B = A$ – объединением будет большее множество из двух.
Например:
Если A = {1;3;5;9}, Β = {3;7;11}, то $A \cup B$ = {1;3;5;7;9;11}.2-4 = 0, x \in \Bbb R\}, B = \{x|x+3 = 2, x \in \Bbb R \}, то A \cup$ B = {-2;-1;2}
Если $A = \{n│n \in \Bbb Z \}$- все целые числа, $B = \{x|x = \frac{a}{b}, a \in \Bbb Z, b \in \Bbb N \}$ — все дроби, то $A \cup B = \{x│x \in \Bbb Q\}$ — множество рациональных чисел. Заметим, что в данном случае $A \subset B$.
Универсум и отрицание
Универсум (универсальное множество) – множество, включающее в себя все множества, рассматриваемые в данной задаче.
В литературе универсум обозначают U.
На диаграммах Эйлера универсум изображают как множество точек прямоугольника, в котором лежат остальные множества:
Примеры универсумов:
При рассмотрении целочисленных задач, универсум – это множество целых чисел.
При построении двумерных графиков, универсум – это множество всех точек координатной плоскости.
При решении вероятностных задач, универсум – это множество всех возможных исходов цепочек событий.
Отрицание (абсолютное дополнение) множества A — множество всех элементов универсума, не принадлежащих A:
$$ \bar{A} = \{x|x \notin A \} $$
Читается «не A».
У отрицания есть любопытное свойство: $\bar{\bar{Α}} = Α $(два раза «нет» — это «да»).
Например:
Если U = {1;2;3;4;5;6;7}, A = {3;4;5}, то $\bar{A} = \{1;2;6;7\}$
Если U = $\{x|x \in \Bbb R\}$ — все действительные числа, A = $\{x|x \gt 0, x \in \Bbb R \}$ — все положительные действительные числа, то $ \bar{A} = \{x|x \le 0, x \in \Bbb R\}$.
Свойства операций пересечения и объединения
Коммутативность
Ассоциативность
$(A \cap B) \cap C = A \cap (B \cap C)$
$ (A \cup B) \cup C = A \cup ( B \cup C) $
Дистрибутивность
$(A \cup B) \cap C = (A \cap C) \cup (B \cap C)$
$ (A \cap B) \cup C = (A \cup C) \cap (B \cup C) $
Идемпотентность
Взаимодействие с отрицанием, пустым множеством и универсумом
$A \cap \bar{A} = \varnothing $
$A \cap U = A$
$A \cap \varnothing = \varnothing$
$A \cup \bar{A} = U $
$A \cup U = U$
$A \cup \varnothing = A$
Законы де Моргана
$ \overline{(A \cap B)} = \bar{A} \cup \bar{B} $
$ \overline{(A \cup B)} = \bar{A} \cap \bar{B} $
Закон поглощения
$ (A \cup B) \cap A = A $
$ (A \cap B) \cup A = A $
Разность множеств
Разностью двух множеств A и B называют множество, в которое входят все элементы из множества A, не принадлежащие множеству B:
$$ A\B = \{x|x \in \Bbb A , x \notin B\} $$
Читается «A без B».
На диаграммах Эйлера разности для пересекающихся множеств выглядят так:
Получается, что отрицание – частный случай разности: $ \bar{A} = \{x|x \in \Bbb U, x \notin A \} $= U\A
«Не A» — это «универсум без A».
Формулы включений и исключений
Рассмотрим два конечных пересекающихся множества A и B.
Пусть число элементов во множествах равно n(A)и n(B) соответственно. А число элементов в пересечении $n(A \cap B)$.
Вопрос: сколько всего элементов в обоих множествах, т.е. чему равно $n(A \cup B)$?
Сумма n(A)и n(B) даст нам больше, чем общее количество, потому что мы два раза посчитаем то, что попадает в пересечение. Значит, если отнять одно пересечение, получится как раз то, что ищем:
$$n(A \cup B) = n(A)+ n(B)-n(A \cap B)$$
Выведем аналогичную формулу для трёх пересекающихся конечных множеств.
Сумма n(A)+ n(B)+n(C) учтёт каждое из парных пересечений по два раза. Поэтому, аналогично задаче с двумя множествами, нужно отнять всё, что попадает в парные пересечения, т.е. отнять сумму $(n(A \cap B)+n(A \cap C)+n(B \cap C) )$. Но после этого получится, что мы лишний раз отняли $n(A \cap B \cap C)$; значит, его нужно «вернуть».
Получаем:
$$ n(A \cup B \cup C) = n(A)+ n(B)+n(C)- $$
$$ -(n(A \cap B)+n(A \cap C)+n(B \cap C) )+n(A \cap B \cap C) $$
Примеры
Пример 1. Найдите пересечение данных множеств:
а) A = {0;5;8;10},
B = {3;6;8;9}
$б) A = \{x|x \lt 3, x \in \Bbb R\}, $
$ B = \{x|x \gt 1, x \in \Bbb R\} $
$A \cap B = \{x|1 \lt x \lt 3, x \in \Bbb R\}$ — отрезок
$в) A = \{x|x \lt 3, x \in \Bbb R\}, $
$ B = \{x|x \gt 1, x \in \Bbb N\} $
$A \cap B = \{x|1 \lt x \lt 3, x \in \Bbb N \} или A \cap B = \{2\}$ — одна точка
г) A = {f|f-правильный многоугольник},
B = {f|f-четырехугольник}
$A \cap B = \{f|f-квадрат\}$
Пример 2. Найдите объединение данных множеств:
а) A = {0;5;8;10}, B = {3;6;8;9}
$A \cup B$ = {0;3;5;6;8;9;10}
б) A = {1;2}, B = {1;2;3;4}
$A \subset B$ – строгое подмножество
$A \cup B $ = B = {1;2;3;4}
$в) A = \{x|x \lt 1, x \in \Bbb R\}, B = \{x|x \gt 1,x \in \Bbb R\} $
$A \cup B = \{x|x \neq 1, x \in \Bbb R \}$
$г) A = \{n│n⋮3, n \in \Bbb Z\}, B = \{n|n⋮9,n \in \Bbb N\} $
$B \subset A$ — строгое подмножество
$ A \cup B = A = \{n│n⋮3, n \in \Bbb Z\} $
Пример 3. Найдите отрицание данного множества на данном универсуме:
а) U = {1;2;3;4;5}, A = {2;3}
б) U = $\{x│x \in \Bbb Q \}$, A = $\{ \frac{4}{5}, \frac{7}{8} \}$
$ \bar{A} = \{x|x \neq \frac{4}{5}, x \neq \frac{7}{8}, x \in \Bbb Q\} $
$в) U = \{x│x \in \Bbb R\}, A = \{x|x \ge 2, x \in \Bbb R\} $
$\bar{A} = \{x|x \lt 2, x \in \Bbb R\}$
Пример 4. Найдите обе разности данных множеств:
а) A = {0;1;2;3;4}, B = {2;4}
A\B = {0;1;3}, $B\A = \{∅\}$
б) A = {0;1;3}, B = {2;4;6}
A\B = {0;1;3}, B\A = {2;4;6}
$в) A = \{x|x \gt 1, x \in \Bbb R\}, $
$ B = \{x|x \lt 3, x \in \Bbb R\} $
A\B $ = \{x|x \ge 3, x \in \Bbb R\}$
B\A $ = \{x|x \le 1,x \in \Bbb R\} $
$ г*) A = \{(x,y)|x \gt 0, x \in \Bbb R, y \in \Bbb R\} $
$ B = \{(x,y)|x \le 5, x \in \Bbb R, y \in \Bbb R\} $
A\B $ = \{(x,y)|x \gt 5, x \in \Bbb R, y \in \Bbb R\} $
B\A $ = \{(x,y)|x \le 0, x \in \Bbb R, y \in \Bbb R\} $
Пример 5. Из 100 студентов умеют программировать на Python 28 человек, на Java 30 человек, на C# 42 человека, на Python и Java 8 человек, на Python и C# 10 человек, на Java и C# 5 человек. Все три языка знают 3 студента. А сколько студентов не умеют программировать на этих языках?
n(U) = 100
n(A) = 28, n(B) = 30, n(C) = 42
$ n(A \cap B) = 8, n(B \cap C) = 5, n(A \cap C) = 10 $
$n(A \cap B \cap C) = 3$
Всего программистов:
$ n(A \cup B \cup C) = n(A)+n(B)+n(C)- $
$ (n(A \cap B)+n(B \cap C)+n(A \cap C) )+n(A \cap B \cap C) $
$n(A \cup B \cup C) = 28+30+42-(8+5+10)+3 = 100-23+3 = 80$
Число не умеющих программировать:
$n(U)-n(A \cup B \cup C) = 100-80 = 20$
Ответ: 20 человек
Объединение и пересечение двух множеств
Все классы статистики включают вопросы о вероятностях, включающих объединение и пересечение множеств. В английском языке мы используем слова «Or» и «And» для описания этих понятий. Например, «Найдите вероятность того, что студент посещает урок математики или естествознания». Это выражает объединение двух множеств словами. «Какова вероятность того, что медсестра имеет степень бакалавра и более пяти лет опыта работы в больнице.«Это выражение пересечения двух множеств. В этом разделе мы научимся расшифровывать эти типы предложений и узнаем о значении объединений и пересечений.
Объединения
Элемент является объединением двух наборов, если он входит в первый набор, второй набор или оба. Символ, который мы используем для объединения, — \ (\ cup \). Слово, которое вы часто будете видеть, обозначающее союз, — это «или».
Пример \ (\ PageIndex {1} \): объединение двух наборов
Лет:
\ [A = \ left \ {2,5,7,8 \ right \} \ nonumber \]
и
\ [B = \ lbrace1,4,5,7,9 \ rbrace \ nonumber \]
Найдите \ (A \ чашка B \)
Решение
Мы включаем в объединение каждое число, которое находится в A или в B:
\ [A \ чашка B = \ left \ {1,2,4,5,7,8,9 \ right \} \ nonumber \]
Пример \ (\ PageIndex {2} \): объединение двух наборов
Рассмотрим следующее предложение: «Найдите вероятность того, что в домохозяйстве меньше 6 окон или дюжина окон.»Запишите это в обозначении набора как объединение двух наборов, а затем запишите это объединение.
Решение
Во-первых, пусть A будет набором количества окон, которое представляет «менее 6 окон». В этот набор входят все числа от 0 до 5:
\ [A = \ left \ {0,1,2,3,4,5 \ right \} \ nonumber \]
Далее, пусть B будет набором количества окон, который представляет «имеет дюжину окон». Это просто набор, который содержит единственное число 12:
\ [B = \ left \ {12 \ right \} \ nonumber \]
Теперь мы можем найти объединение этих двух наборов:
\ [A \ чашка B = \ left \ {0,1,2,3,4,5,12 \ right \} \ nonumber \]
Перекрестки
Элемент находится на пересечении двух наборов, если он находится в первом наборе, и он находится во втором наборе.Символ, который мы используем для перекрестка, — \ (\ cap \). Часто встречающееся слово, обозначающее перекресток, — это «и».
Пример \ (\ PageIndex {3} \): пересечение двух множеств
Лет:
\ [A = \ left \ {3,4,5,8,9,10,11,12 \ right \} \ nonumber \]
и
\ [B = \ lbrace5,6,7,8,9 \ rbrace \ nonumber \]
Найдите \ (A \ cap B \).
Решение
Мы включаем в пересечение только те числа, которые находятся в A и B:
\ [A \ cap B = \ left \ {5,8,9 \ right \} \ nonumber \]
Пример \ (\ PageIndex {4} \): пересечение двух множеств
Рассмотрим следующее предложение: «Найдите вероятность того, что количество единиц, которые издает студент, больше 12 единиц и меньше 18 единиц.»Предполагая, что учащиеся берут только целое количество единиц, запишите это в обозначениях набора как пересечение двух наборов, а затем запишите это пересечение.
Решение
Во-первых, пусть A будет набором чисел единиц, который представляет «более 12 единиц». В этот набор входят все числа от 13 до бесконечности:
\ [A = \ left \ {13, \: 14, \: 15, \: … \ right \} \ nonumber \]
Далее, пусть B будет набором количества единиц, которое представляет «менее 18 единиц».Это набор, содержащий числа от 1 до 17:
\ [B = \ left \ {1, \: 2, \: 3, \: …, \: 17 \ right \} \ nonumber \]
Теперь мы можем найти пересечение этих двух множеств:
\ [A \ cap B = \ left \ {13, \: 14, \: 15, \: 16, \: 17 \ right \} \ nonumber \]
Объединение союзов, пересечений и дополнений
Одна из самых сложных задач в статистике — расшифровать предложение и превратить его в символы. Это может быть особенно сложно, когда есть предложение, в котором нет слов «объединение», «пересечение» или «дополнение», но оно неявно относится к этим словам.Лучший способ овладеть этим навыком — практиковаться, практиковаться и еще больше практиковаться.
Пример \ (\ PageIndex {5} \)
Рассмотрим следующее предложение: «Если вы бросаете шестигранный кубик, найдите вероятность того, что он не четный и не 3». Запишите это в обозначениях набора.
Решение
Во-первых, пусть A будет набором четных чисел, а B будет набором, содержащим только 3. Мы можем написать:
\ [A = \ left \ {2,4,6 \ right \}, \: \: \: B \: = \: \ left \ {3 \ right \} \ nonumber \]
Далее, поскольку мы хотим «даже не», нам нужно рассмотреть дополнение A:
\ [A ^ c = \ left \ {1,3,5 \ right \} \ nonumber \]
Точно так же, поскольку мы хотим «не 3», нам нужно рассмотреть дополнение B:
\ [B ^ c = \ left \ {1,2,4,5,6 \ right \} \ nonumber \]
Наконец, мы замечаем ключевое слово «и».c = \: \ left \ {1,3,5 \ right \} \ cap \ left \ {1,2,4,5,6 \ right \} = \ left \ {1,5 \ right \} \ nonumber \]
Пример \ (\ PageIndex {6} \)
Рассмотрим следующее предложение: «Если вы случайным образом выберете человека, найдите вероятность того, что этот человек старше 8 лет или одновременно моложе 6 лет и не моложе 3». Запишите это в обозначениях набора.
Решение
Во-первых, пусть A будет группой людей старше 8 лет, B будет группой людей младше 6 лет, а C будет группой людей младше 3 лет.c \ right) = \: \ left \ {x \ mid x> 8 \ right \} \ cup \ left \ {x \ mid3 \ le x <6 \ right \} \ nonumber \]
Самый ясный способ отобразить это объединение — на числовой прямой. В числовой строке ниже отображается ответ:
.Упражнение
Предположим, что мы выбираем человека наугад и хотим выяснить вероятность того, что месяц его рождения наступил после июля, а не после сентября. Запишите это событие, используя обозначение набора.
Союз наборов | Math Goodies
В предыдущих уроках мы использовали диаграммы Венна для представления отношений между множествами.Давайте посмотрим на пример 1 ниже.
Пример 1: В средней школе Гринвилля два класса будут объединены в один, чтобы сократить расходы. Если учеников Band и Chorus объединить в один новый класс, то какие ученики будут в этом классе?
Дано: Дано = {Сэм, Кеша, Дерек, Лорри, Робин, Рауль, Ширли, Натан, Крис, Дана} , Группа = {Сэм, Лорри, Рауль, Дерек} и Припев = {Робин, Дерек, Кеша}, найдите Band Chorus.
Анализ: Эта проблема просит нас найти союз оркестра и хора.Чтобы решить эту проблему, мы должны перечислить всех студентов, которые участвуют в оркестре, хоре или и том и другом.
Решение:
Пояснение:
Band Припев = {Сэм, Лорри, Рауль, Дерек, Кеша, Робин}
Обратите внимание, что Дерек находится в обоих наборах и, следовательно, на их пересечении. Однако Дерек записан только один раз в союзе.
Определение: Объединение из двух наборов A и B, — это набор элементов, которые находятся в A или в B или в обоих.Он обозначается как A B , и читается как « A, соединение B ».
Сравним объединение и пересечение.
| Союз | Перекресток | |
| записывается как | A B | A B |
| читать как | A штуцер B | A пересечение B |
| значение | A или B или оба | A и B |
| как найти | объединить все элементы | найти элементы, общие для обоих |
Под союзом часто понимают брак.Мы используем «и» для пересечения и « или» для объединения. Давайте рассмотрим еще несколько примеров объединения двух множеств.
Пример 2: Пусть = {подсчет чисел}, P = {кратное 3 меньше 20} и Q = {четные числа меньше 20}. Нарисуйте и обозначьте диаграмму Венна, чтобы показать объединение P и Q .
Анализ: Элементы оттенка, которые находятся в P или в Q или в обоих. Заштрихованная область на приведенной ниже диаграмме Венна обозначает P Q.
Решение:
Обозначение: P Q = {2, 3, 4, 6, 8, 9, 10, 12, 14, 15, 16, 18}
Обратите внимание, что элементы 6, 12 и 18 находятся в обоих наборах (т.е. на пересечении P и Q ). Однако эти элементы записываются в объединении только один раз.
Пример 3: Пусть = { k | 1 ≤ k ≤ 10}, X = {1, 6, 9} и Y = {1, 3, 5, 6, 8, 9}.Нарисуйте и пометьте диаграмму Венна, чтобы показать X Y.
Анализ: X является подмножеством Y . Таким образом, все элементы в X также содержатся в Y .
Пояснение: X Y = {1, 3, 5, 6, 8, 9}, что равно набору Y.
В примере 3, поскольку X Y , мы получаем, что X Y4Эти отношения определены ниже.
Другой способ определить объединение двух множеств:
A B = {x | x A или x B }
Пример 4: Let = {животные}, A = {10 собак} и B = {20 кошек}. Нарисуйте и обозначьте диаграмму Венна, чтобы показать A B .
Анализ: Эти множества не пересекаются и не имеют общих элементов. Таким образом, A B — это все элементы в A и все элементы в B.
Пояснение: A B = {10 собак, 20 кошек}
Пример 4 представляет собой прямое объединение двух наборов. Непересекающиеся множества не имеют общих элементов. Следовательно, объединение A и B не имеет общих элементов.Поскольку невозможно, чтобы собаки в A были также кошками в B , мы уверены, что количество элементов в объединении является суммой всех собак в A и всех кошек в B . Таким образом, объединение является результатом сложения всех элементов в обоих наборах.
Соединение из двух наборов A и B, — это набор элементов, которые находятся в A или в B или в обоих. Он обозначается A B , и читается как « A, соединение B ».Формальное определение союза показано ниже:
A B = {x | x A или x B }
Упражнения
Указания: нарисуйте и обозначьте диаграмму Венна, чтобы помочь вам ответить на каждый из приведенных ниже вопросов. Выберите свой ответ, нажав соответствующую кнопку. Отзыв на ваш ответ представлен в БЛОКЕ РЕЗУЛЬТАТОВ.Если вы допустили ошибку, переосмыслите свой ответ, а затем выберите другую кнопку.
| 1. | Дано = {яблоки, апельсины, бананы, груши} и = {апельсины, груши, виноград}, что такое ? |
| 2. | Учитывая = {простые числа} и = {составные числа}, что такое ? |
| 3. | Учитывая = {1, 4, 16} и = {1, 4, 9, 16, 25, 36}, что такое ? |
| 4. | Учитывая = {гласные} и = {согласные}, что такое ? |
| 5. | Что из следующего верно относительно приведенной ниже диаграммы Венна? |
| | |
| B ‘ = {2, 3, 9} B = {0, 1, 4, 5, 6, 7, 8} = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} Все вышеперечисленное. БЛОК РЕЗУЛЬТАТОВ: |
проблем на пересечении трех наборов
Covid-19 привел мир к феноменальному переходу.
Электронное обучение — это будущее уже сегодня.
Оставайтесь дома, оставайтесь в безопасности и продолжайте учиться !!!
В этом разделе мы рассмотрим некоторые практические задачи о пересечении трех множеств.Для решения такой задачи мы должны учитывать следующие правила:
Если A, B и C — три конечных множества, то:
1) n (A ∪ B ∪ C) =
n (A) + n (B) + n (C) — n (A ∩ B) — n (B ∩ C)
— n (A ∩ C) + n (A ∩ B ∩ C)
2) n [A ∩ (B ∪ C)] = n (A ∩ B) + n (A ∩ C) — n (A ∩ B ∩ C)
Задачи на пересечении трех наборов:1) При опросе 200 учеников школы было обнаружено, что 120 изучают математику, 90 изучают физику и 70 изучают химию, 40 изучают математику и физику, 30 изучают физику и химия, 50 изучают химию и математику, а 20 изучают ни один из этих предметов.Найдите количество студентов, изучающих все три предмета.
Решение:M = Математика; P = Физика и C = Химия
n (M) = 120 n (P) = 90 n (C) = 70 n (M ∩ P) = 40
n (P ∩ C) = 30 n (C ∩ M) = 50 n (M ∪ P ∪ C) ‘= 20
Теперь n (M ∪ P ∪ C)’ = n (U) — n (M ∪ P ∪ C)
20 = 200 — n (M ∪ P ∪ C)
Следовательно, n (M ∪ P ∪ C) = 200-20 = 180
n (M ∪ P ∪ C)
= n (M) + n (P) + n (C) — n (M ∩ P) — n (P ∩ C) — n (C ∩ M) + n (M ∩ P ∩ C)
180 = 120 + 90 + 70-40-30-50 + n (M ∩ P ∩ C)
⇒ n (M ∩ P ∩ C) = 180 — 120 — 90 — 70 + 40 + 30 + 50
⇒ n (M ∩ P C) = 20.
2) При опросе 60 человек было обнаружено, что 25 человек читают газету H, 26 читают газету T, 26 читают газету I, 9 читают и H, и I, 11 читают и H, и T, 8 читают и T, и Я, 3 года, читаю все три газеты. Найдите количество людей, которые читают хотя бы одну из газет. (Задачи на пересечении трех наборов)
Решение:H = Люди, которые читают газету H.
I = Люди, которые читают газету I.
T = Люди кто читает газету T.
n (H) = 25; n (T) = 26; n (I) = 26; n (H I) = 9
n (H T) = 11; n (T ∩ I) = 8 и n (H ∩ T ∩ I) = 3
n (H ∪T ∪ I) = количество людей, которые читают хотя бы одну из газет
= n (H) + n (T) + n (I) — n (H ∩ T) — n (T ∩ I) — n (H ∩ I) + n (H ∩ T ∩ I)
n (H ∪T ∪ I) = 25 + 26 + 26 — 11 — 9 — 8 + 3
= 77 — 28 + 3
= 80 — 28
= 52
Следовательно, количество людей, которые читают хотя бы одну из газет, составляет 52 человека.
Теория множеств
• Множества
• Представление множества
• Кардинальное число
• Типы множеств
• Пары множеств
• Подмножество
• Дополнение к множеству
• Объединение множеств
• Пересечение множеств
• Операции на множествах
• Закон Де Моргана
• Диаграммы Венна
• Диаграммы Венна для множеств
• Диаграммы Венна для различных ситуаций
• Задачи на пересечении двух множеств
• Задачи на пересечении трех множеств
Covid -19 повлияло на физическое взаимодействие между людьми.
Не позволяйте этому влиять на ваше обучение.
теория множеств | Символы, примеры и формулы
Теория множеств , раздел математики, который имеет дело со свойствами четко определенных наборов объектов, которые могут иметь или не иметь математическую природу, например числа или функции. Теория менее ценна в прямом применении к обычному опыту, чем как основа для точной и адаптируемой терминологии для определения сложных и изощренных математических понятий.
Между 1874 и 1897 годами немецкий математик и логик Георг Кантор создал теорию абстрактных множеств сущностей и превратил ее в математическую дисциплину. Эта теория выросла из его исследований некоторых конкретных проблем, касающихся определенных типов бесконечных множеств действительных чисел. Набор, как писал Кантор, представляет собой совокупность определенных, различимых объектов восприятия или мысли, задуманных как единое целое. Объекты называются элементами или членами набора.
Теория имела революционный аспект рассмотрения бесконечных множеств как математических объектов, которые находятся на равных с теми, которые могут быть построены за конечное число шагов.Со времен античности большинство математиков тщательно избегали введения в свои аргументы фактической бесконечности (т. Е. Множеств, содержащих бесконечное количество объектов, рассматриваемых как существующие одновременно, по крайней мере, мысленно). Так как это отношение сохранялось почти до конца XIX века, работа Кантора подвергалась серьезной критике в связи с тем, что она касалась вымысла — более того, что она посягала на сферу философии и нарушала принципы религии. Однако как только начали находить приложения к анализу, отношение начало меняться, и к 1890-м годам идеи и результаты Кантора получили признание.К 1900 году теория множеств была признана отдельной отраслью математики.
Однако именно тогда было обнаружено несколько противоречий в так называемой наивной теории множеств. Для устранения таких проблем была разработана аксиоматическая основа теории множеств, аналогичная той, которая была разработана для элементарной геометрии. Степень успеха, достигнутого в этом развитии, а также нынешний уровень теории множеств были хорошо выражены в Николя Бурбаки Éléments de mathématique (начат в 1939 г .; «Элементы математики»): известно, что логически можно вывести практически всю известную математику из единого источника — теории множеств.”
Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишись сейчасВведение в теорию наивных множеств
Основные концепции множеств
В теории наивных множеств набор — это совокупность объектов (называемых членами или элементами), которые рассматриваются как один объект. Чтобы указать, что объект x является членом набора A , пишут x ∊ A , а x ∉ A указывает, что x не является членом A .Набор может быть определен правилом членства (формулой) или перечислением его членов в фигурных скобках. Например, набор, заданный правилом «простые числа меньше 10», также может быть задан как {2, 3, 5, 7}. В принципе, любое конечное множество может быть определено явным списком его членов, но для определения бесконечных множеств требуется правило или шаблон, указывающий на членство; например, многоточие в {0, 1, 2, 3, 4, 5, 6, 7,…} указывает, что список натуральных чисел ℕ продолжается бесконечно. Пустой (или void, или null) набор, обозначенный {} или Ø, не содержит вообще никаких элементов.Тем не менее, он имеет статус набора.
Набор A называется подмножеством набора B (обозначается A ⊆ B ), если все элементы A также являются членами B . Например, любой набор является подмножеством самого себя, а Ø — подмножеством любого набора. Если и A ⊆ B и B ⊆ A , то A и B имеют точно такие же элементы. Часть концепции набора состоит в том, что в этом случае A = B ; то есть A и B — это один и тот же набор.
Пересечение наборов
Этот урок объяснит, как найти пересечение множеств. Начнем с определения пересечения двух множеств.Определение:
Для двух наборов A и B пересечение — это набор, который содержит элементы или объекты, принадлежащие A и B одновременно.
Мы пишем A B
В основном, мы находим A ∩ B, ища все общие элементы A и B. Далее проиллюстрируем примерами.
Пример №1 .
Чтобы упростить задачу, обратите внимание, что общее у них выделено жирным шрифтом.
Пусть A = { 1 апельсин , 1 ананас, 1 банан, 1 яблоко } и B = {1 ложка, 1 апельсин , 1 нож, 1 вилка, 1 яблоко }
A ∩ B = {1 апельсин, 1 яблоко}
Пример 2 .
Найдите точку пересечения A и B, а затем составьте диаграммы Венна.
A = { b , 1, 2, 4 , 6} и B = { 4 , a, b , c, d, f}
A ∩ B = {4, б}
Пример № 3 .
A = {x / x число больше 4 и меньше 8}
B = {x / x положительное число меньше 7}
A = { 5 , 6 , 7} и B = {1, 2, 3, 4, 5 , 6 }
A ∩ B = {5, 6}
Или A ∩ B = {x / x — число больше 4 и меньше чем 7}
Пример № 4 .
A = {x / x — страна в Азии}
B = {x / x — страна в Африке}
Поскольку нет одинаковых стран в Азии и Африке, перекресток пуст.
A ∩ B = {}
Пример № 5 .
A = {#,%, &, *, $}
B = {}
Это тонкий пример! Поскольку пустой набор включен в любой набор, он также включен в A, хотя вы его не видите.
Таким образом, пустое множество — это единственное, что общего между наборами A и B.
A ∩ B = {}
Определение объединения трех наборов:
Для трех наборов A, B и C пересечение — это набор, который содержит элементы или объекты, принадлежащие A, B и C одновременно.
Мы пишем A B ∩ C
В основном, мы находим A ∩ B ∩ C, ища все общие элементы A, B и C.
A = { # , 1, 2, 4 , 6}, B = { # , a, b, 4 , c} и C = A = { # ,%, &, * , $, 4 }A ∩ B ∩ C = {4, #}
На графике ниже показана заштрихованная область пересечения двух наборов
На графике ниже показана заштрихованная область пересечения трех множеств
На этом заканчивается урок о пересечении множеств.Если у вас есть вопросы о пересечении множеств, я с радостью отвечу на них.
Используйте тест ниже, чтобы увидеть, насколько хорошо вы можете найти пересечение множеств.
Введение в физику
18 ноя, 20 13:20
Первоклассное введение в физику. Универсальный ресурс для глубокого понимания важных концепций физики
Подробнее
Новые уроки математики
Ваша электронная почта в безопасности.Мы будем использовать его только для информирования вас о новых уроках математики.
математических наборов: элементы, пересечения и союзы — класс математики в колледже (видео)
Соединения
Для объединения наборов мы используем термин Соединение . Мы объединяем комплекта в один.
Допустим, у меня есть два комплекта. Set A — зеленый, синий и розовый. Набор B оранжевый, желтый и черный. A u B представляет собой объединение наборов A и B .Да, этот символ и олицетворяет союз! Это вроде как удобно! A u B представляет все элементы, которые перечислены в наборе A , или в наборе B , или в обоих. Как это будет выглядеть при использовании математических символов? A u B = {зеленый, синий, розовый, оранжевый, желтый, черный}.
Пересечения
Чтобы найти элементы, общие с наборами, мы используем термин перекресток . Думайте о наборах как о двух дорогах, которые встречаются на перекрестке. Что общего у этих двух дорог или наборов?
Допустим, у меня есть два комплекта.Набор A равен 4, 6 и 9. Набор B равен 7, 8 и 9. Пересечение B представляет собой пересечение наборов A и B . Да, этот перевернутый и представляет собой перекресток! Здесь представлены все элементы, одинаковые в A и B . Как это будет выглядеть при использовании математических символов? A пересекает B = {9}.
Итоги урока
Давайте рассмотрим то, о чем мы только что говорили.Набор — это набор предметов. Это могут быть цифры, буквы, что угодно. Чтобы показать набор, мы всегда используем заглавную букву. Чтобы показать элементы или элементы набора, они всегда помещаются в фигурные скобки, {} или эти фигурные скобки. Union — это когда мы объединяем вещи — когда мы собираемся соединить их. Итак, A u B означает, что мы собираемся поместить все в A вместе со всем в B . Помните, перекресток — это то же место, где они пересекаются.Итак, если я скажу, что A пересекает B , я ищу любые элементы или элементы, которые являются общими в A и B .
Результат обучения
После просмотра этого урока вы должны быть в состоянии определить концепции множеств, таких как элементы, и то, как они связаны посредством объединения и пересечения.
Пересечение — ACT Math
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; и Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
.




 Решите примеры, расположите ответы в порядке возрастания и расшифруйте слово. (Слайд 2-4)
Решите примеры, расположите ответы в порядке возрастания и расшифруйте слово. (Слайд 2-4)

 Запишите.
Запишите.

 Сколько учеников в нашем классе?
Сколько учеников в нашем классе?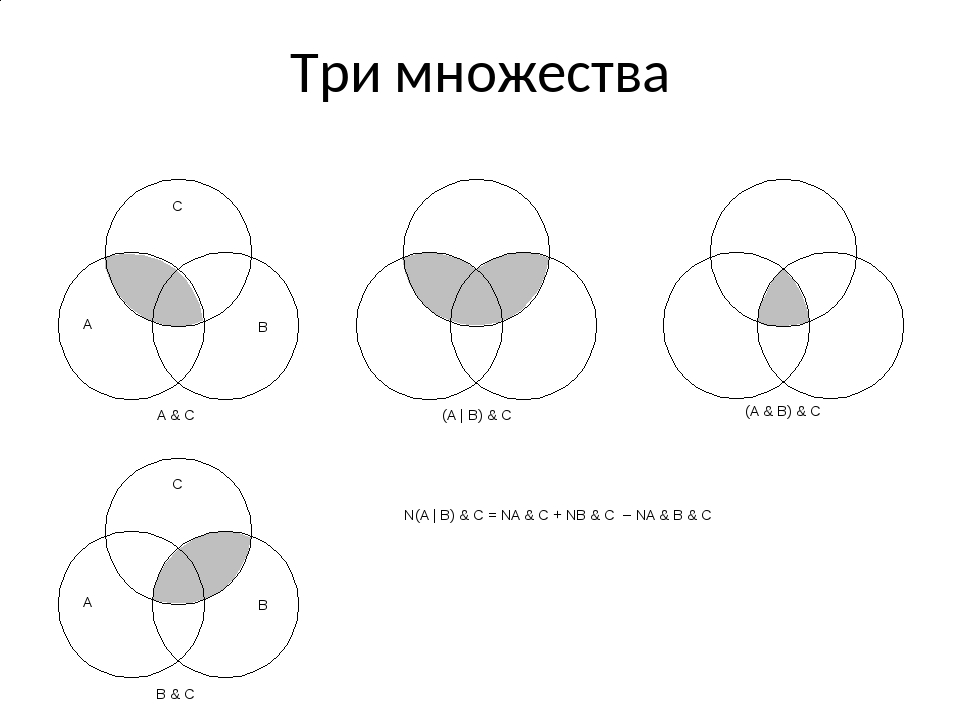 Сколько учеников этого класса любят яблоки?
Сколько учеников этого класса любят яблоки? Сколько человек из этих 100 знают три языка?
Сколько человек из этих 100 знают три языка?
 п.
п.