Диаграмма эйлера венна 3 класс петерсон: Урок 5. Диаграмма Эйлера — Венна

Урок 5. Диаграмма Эйлера — Венна

Класс

• 1 класс

• 2 класс

  • Английский язык
  • Математика

• 3 класс

  • Русский язык
  • Английский язык
  • Математика

• 4 класс

  • Русский язык
  • Английский язык
  • Математика

• 5 класс

  • Русский язык
  • Английский язык
  • Математика
  • Биология

• 6 класс

  • Русский язык
  • Английский язык
  • Математика
  • Биология

• 7 класс

  • Русский язык
  • Английский язык
  • Математика
  • Биология
  • Физика
  • Химия

• 8 класс

  • Русский язык
  • Английский язык
  • Математика
  • Биология
  • Физика
  • Химия

• 9 класс

  • Русский язык
  • Английский язык
  • Математика
  • Биология
  • Физика
  • Химия

• 10 класс

  • Английский язык
  • Биология
  • Физика
  • Химия

• 11 класс

  • Английский язык
  • Биология
  • Химия

3 КЛАСС

Урок 5.

Диаграмма Эйлера — Венна

Внимательно прочитай решение

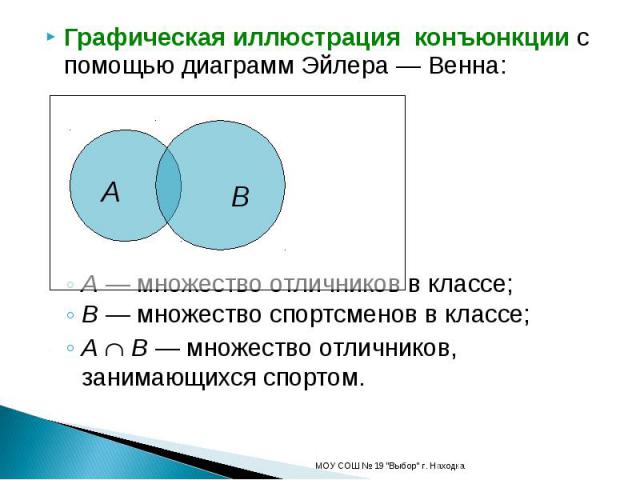
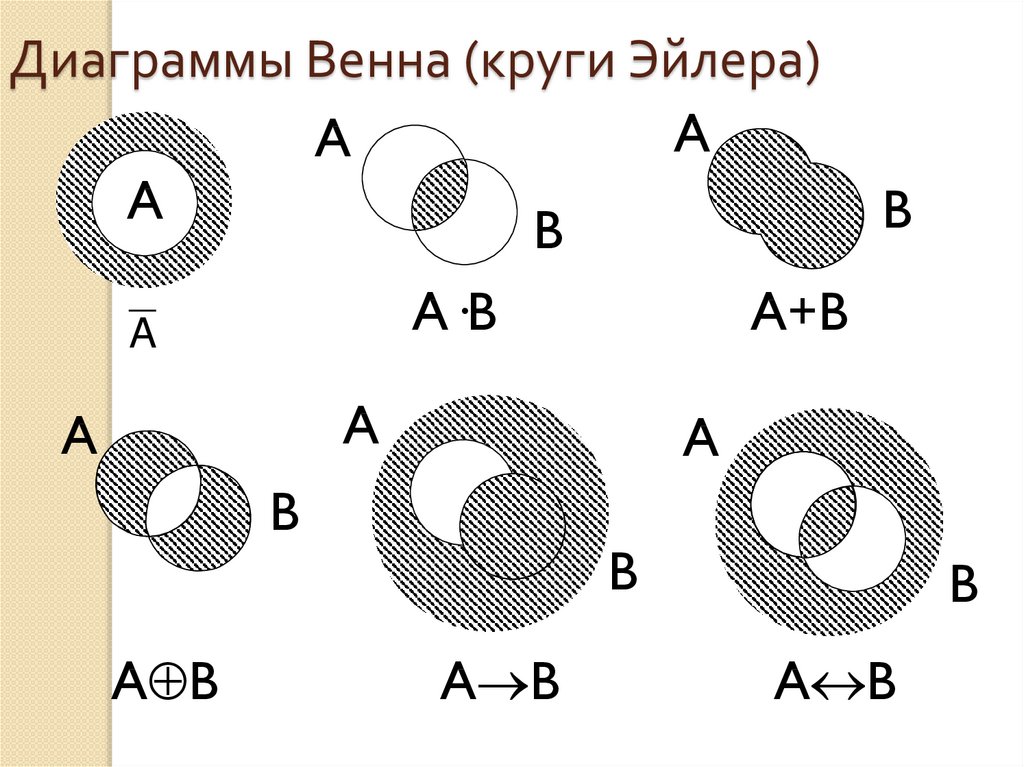
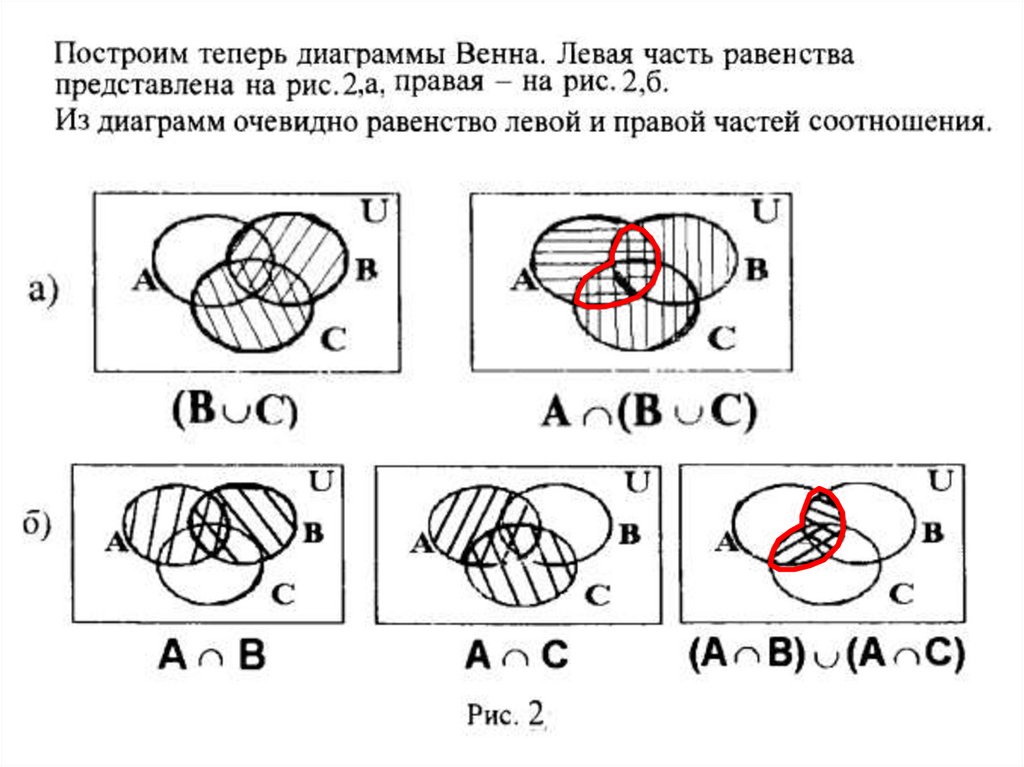
Чтобы  лучше  представить  себе  множество,  можно  использовать  рисунок,  называемый  диаграммой  Эйлера–Венна.  Это  замкнутая  линия,  внутри  которой  расположены  элементы  данного  множества,  а  снаружи  –  элементы,  не  принадлежащие  множеству. 

Чтобы  лучше  представить  себе  множество,  можно  использовать  рисунок,  называемый  диаграммой  Эйлера–Венна.  Это  замкнутая  линия,  внутри  которой  расположены  элементы  данного  множества,  а  снаружи  –  элементы,  не  принадлежащие  множеству. 

Чтобы  лучше  представить  себе  множество,  можно  использовать  рисунок,  называемый  диаграммой  Эйлера–Венна.  Это  замкнутая  линия,  внутри  которой  расположены  элементы  данного  множества,  а  снаружи  –  элементы,  не  принадлежащие  множеству. 

Чтобы  лучше  представить  себе  множество,  можно  использовать  рисунок,  называемый  диаграммой  Эйлера–Венна.  Это  замкнутая  линия,  внутри  которой  расположены  элементы  данного  множества,  а  снаружи  –  элементы,  не  принадлежащие  множеству.  

Выпиши все трехзначные числа, у которых все цифры одинаковые

Девочка и с мячом и с цветком принадлежит множествам А и В

Остаток всегда меньше делителя

Остаток должен быть меньше делителя

Остаток всегда меньше делителя

Если используем предлог "в" значит умножаем

Умение правильно и быстро считать помогает в дальнейшем изучении математики

Первым делай действия в скобочках

Ответь кратко на вопросы

От перестановки мест слагаемых сумма не меняется

логические задачи хорошо развивают математическое мышление

Вопросники:

Вопрос:

Вопрос:

Пропуски:

Ответы Задание 3 1 Часть Урок 5. Диаграмма Эйлера-Венна. Знаки ГДЗ по математике 3 класс рабочая тетрадь Петерсон 1, 2, 3 часть ответы

1 Часть

Повторение

1234567891011

Урок 1. Множество и его элементы

1234

Урок 2. Способы задания множеств

123456

Урок 3. Равные множества.

Пустое множество 123456

Урок 4. Решение задач

12345

Урок 5. Диаграмма Эйлера-Венна. Знаки

123456

Урок 6. Решение задач

12345

Урок 7. Подмножество. Знаки

1234

Урок 8. Задачи на приведение к единице

1234

Урок 9. Решение задач

12345

Урок 10. Пересечение множеств. Знак

1234567

Урок 11. Свойства пересечения множеств

12345678

Урок 12. Решение задач

1234

Урок 13. Обратные задачи на приведение к единице

12345678

Урок 14. Объединение множеств. Знак

1234

Урок 15. Решение задач

1234

Урок 16. Умножение в столбик — 24 на 8

12345

Урок 17. Свойства объединения множеств

1234

Урок 18. Разбиение множества на части

1234

Урок 19. Решение задач

123

Урок 22. Многозначные числа

12345

Урок 23. Сравнение натуральных чисел

1234

Урок 24. Решение задач

123456

Урок 25. Сумма разрядных слагаемых

123456

Урок 26. Сложение и вычитание многозначных чисел

123456

Урок 27.

Решение задач 12345

Урок 28. Преобразование единиц счета

12345

Урок 29. Решение задач

12

Урок 30. Порядок действий. Свойства действий

12345

Урок 31. Решение задач

12345

Урок 32. Решение задач

12345

Урок 33. Умножение на 10, 100, 1000…

123456

Урок 34. Умножение круглых чисел

123456

Урок 35. Решение задач

123

Урок 36. Умножение круглых чисел

123456

Урок 37. Деление круглых чисел

123456

Урок 38. Решение задач

1234

Урок 39. Единицы длины

12345

Урок 40. Решение задач

1234

Урок 41. Единицы массы

123456

Урок 42. Решение задач

1234

Урок 43. Решение задач

123

2 Часть

Урок 1. Умножение на однозначное число

12345678910

Урок 2. Умножение круглых чисел в столбик

123456

Урок 3. Решение задач

1234

Урок 4. Нахождение чисел по их сумме и разности

123456

Урок 5. Решение задач

1234

Урок 6. Деление на однозначное число углом

12345

Урок 7.

Решение задач 12345

Урок 8. Деление на однозначное число углом 312 3

123456

Урок 9. Деление на однозначное число углом — 460 на 2

12345

Урок 10. Решение задач

1234

Урок 11. Деление на однозначное число углом (без остатка)

123456

Урок 12. Решение задач

123456

Урок 13. Деление круглых чисел с остатком

1234

Урок 14. Решение задач

123

Урок 15. Преобразование фигур

123456

Урок 16. Симметрия относительно прямой

1234

Урок 17. Преобразование фигур

1234

Урок 18. Симметрия фигуры

1234

Урок 19. Решение задач

12345

Урок 20. Решение задач

123

Урок 21. Меры времени. Календарь

123456

Урок 22. Таблица мер времени

123456

Урок 23. Решение задач

1234567

Урок 24. Меры времени — час, минута, секунда

12345

Урок 25. Часы

123456

Урок 26. Решение задач

1234

Урок 27. Преобразование единиц времени

1234

Урок 28. Решение задач

12345

Урок 29.

Переменная 123456

Урок 30. Выражение с переменной

123456

Урок 31. Верно и неверно. Высказывания

12345

Урок 32. Равенства и неравенства

12345

Урок 33. Решение задач

12

Урок 34. Уравнения

12345

Урок 35. Упрощение записи уравнений

12

Урок 36. Составные уравнения

1234

Урок 37. Решение задач

1234

Урок 38. Формулы

1234

Урок 39. Формула объема параллелепипеда

12345

Урок 40. Решение задач

1234

Урок 41. Формула деления с остатком

12345

Урок 42. Решение задач

123456

3 Часть

Урок 1. Скорость. Время. Расстояние

12345

Урок 2. Формула пути

12345678

Урок 3. Решение задач

1234

Урок 4. Формулы зависимостей

1234

Урок 5. Формулы зависимостей между величинами

1234567

Урок 6. Решение задач

1234

Урок 7. Задачи на движение

12345

Урок 8. Задачи на движение

1234567

Урок 9. Решение задач

123

Урок 10.

Решение задач 123

Урок 11. Решение задач

123

Урок 12. Умножение на двузначное число

12345

Урок 13. Формула стоимости

123456789

Урок 14. Решение задач

12345

Урок 15. Умножение круглых многозначных чисел

1234

Урок 16. Задачи на стоимость

1234567

Урок 17. Решение задач

1234

Урок 18. Умножение на трехзначное число

1234567

Урок 19. Умножение на трехзначное число 312 на 201

1234

Урок 20. Решение задач

12345

Урок 21. Формула работы

12345678

Урок 22. Задачи на работу

123456

Урок 23. Решение задач

123

Урок 24. Формула произведения

123456

Урок 25. Решение задач

1234

Урок 26. Способы решения составных задач

123456

Урок 27. Решение задач

12

Урок 28. Умножение многозначных чисел

123

Урок Повторение

123456789101112131415161718192021222324252627282930313233343536373839404142434445

Средняя оценка 0 / 5. Количество оценок: 0

Оценок пока нет.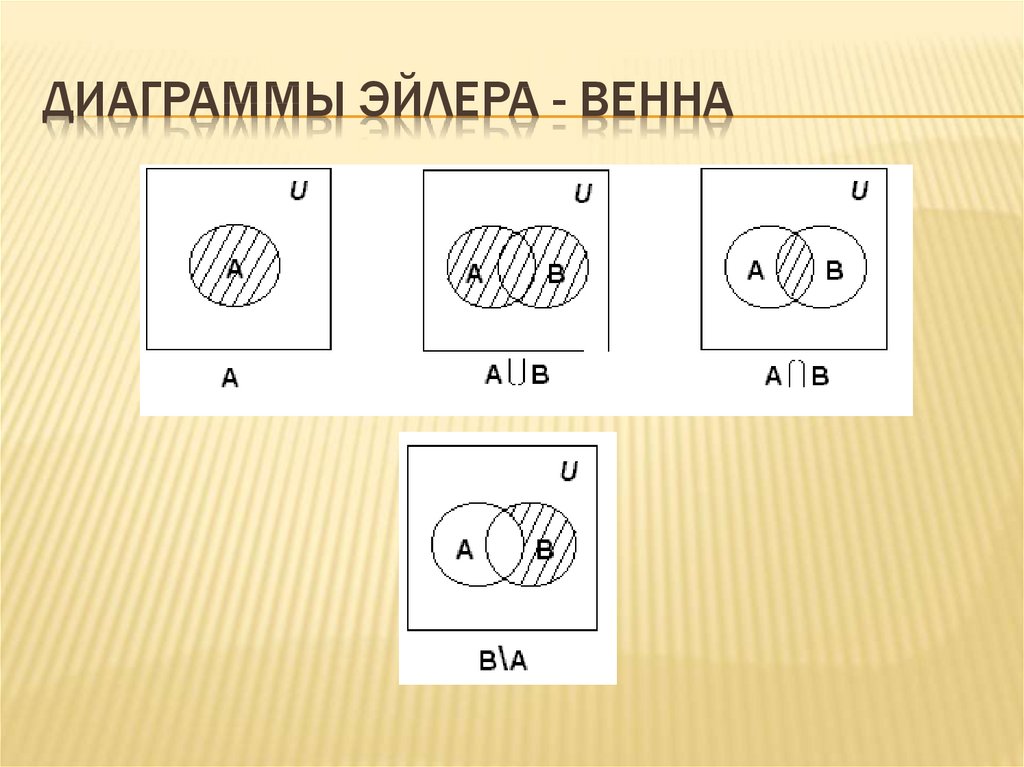 Поставьте оценку первым.

Галерея диаграмм Эйлера и Венна

Галерея диаграмм Эйлера и Венна

 библиотека (эйлерр) 

Эта виньетка служит галереей для диаграмм Эйлера и демонстрацией различных доступных вариантов настройки.

Равномерные пересечения

 uniform_intersections <- euler(c("A" = 10, "B" = 10, "C" = 10,
                                 "А&В" = 4, "А&В" = 4, "В&В" = 4,
                                 "А&В&С" = 2))
сюжет (uniform_intersections) 

Непересекающиеся множества

 disjoint_sets <- euler(c(A = 1, B = 1, C = 1))
сюжет (непересекающиеся_множества,
     labels = c("Том", "Грег", "Альберта"),
     ребра = список(lty = 1:3)) 

Множество, содержащееся в пересечении двух множеств

 полностью_содержащее <- euler(c("A" = 15, "B" = 15, "C" = 0 ,
                                «А и В» = 3, «А и С» = 0, «В и С» = 0,
                                "А&В&С" = 3))
сюжет (полностью_содержащий,
     labels = list(col = c("белый", "черный", "черный")),
     края = список (столбец = «белый», lex = 2),
     fills = c("черный", "голубой", "оранжевый")) 

Два множества пересекаются внутри третьего

 intersecting_inside <- euler(c("A" = 15, "B" = 0, "C" = 0,
                               «А и В» = 3, «А и С» = 3, «В и С» = 0,
                                "А&В&С" = 2))
сюжет (intersecting_inside,
     заполняет = список (заполняет = c ("лавандаblush3",
                           "голубой2",
                           "светлый лосось",
                           "",
                           "",
                           "",
                           "слива2")),
     легенда = список (сторона = "право")) 

Сложный набор (для кружков!)

 one_contained <- euler(c("A" = 7, B = 6, C = 0,
                         «А&В» = 0, «А&В» = 1, «В&В» = 1,
                         "А&В&С" = 2),
                       форма = "эллипс")
сюжет (one_contained,
     количество = список(тип = "процент")) 

Матрешка

Наборы пересекаются внутри других наборов.

 russian_doll <- euler(c("A" = 15, "B" = 0, C = 0,
                        «А и В» = 10, «А и С» = 0, «В и С» = 0,
                        "А&В&С" = 5))
сюжет(русская_кукла) 

Связь множества Уилкинсона

Эта связь множества взята из Wilkinson et al. Лучше всего работает с эллипсами.

 Уилкинсон <- euler(c(A = 4, B = 6, C = 3, D = 2, E = 7, F = 3,
                     "A&B" = 2, "A&F" = 2, "B&C" = 2, "B&D" = 1,
                     "Б&Ф" = 2, "К&Д" = 1, "Д&Э" = 1, "Э&Ф" = 1,
                     "A&B&F" = 1, "B&C&D" = 1),
                   форма = "эллипс")
сюжет (Уилкинсон,
     метки = список (семейство шрифтов = "с засечками"),
     края = список (lty = 3),
     количество = список (тип = "процент",
                       шрифт = 3)) 

Набор генов

 гены <- euler(c("SE" = 13, "Лечить" = 28, "Анти-КПК" = 101, "DAS28" = 91,
                 «SE&Treat» = 1, «SE&DAS28» = 14, «Treat&Anti-CCP» = 6,
                 "SE&Анти-КПК&DAS28" = 1))
сюжет (гены,
     количество = список (тип = c ("проценты", "числа"))) 

Три множества, пересекающиеся внутри четвертого

 three_inside_fourth <- euler(c ("A" = 30,
                               "A&B" = 3, "A&C" = 3, "A&D" = 3,
                               "A&B&C" = 2, "A&B&D" = 2, "A&C&D" = 2,
                               "А&В&С&D" = 1))
участок (три_внутри_четвертого) 

Комбинация eulerAPE

Комбинация из статьи eulerAPE.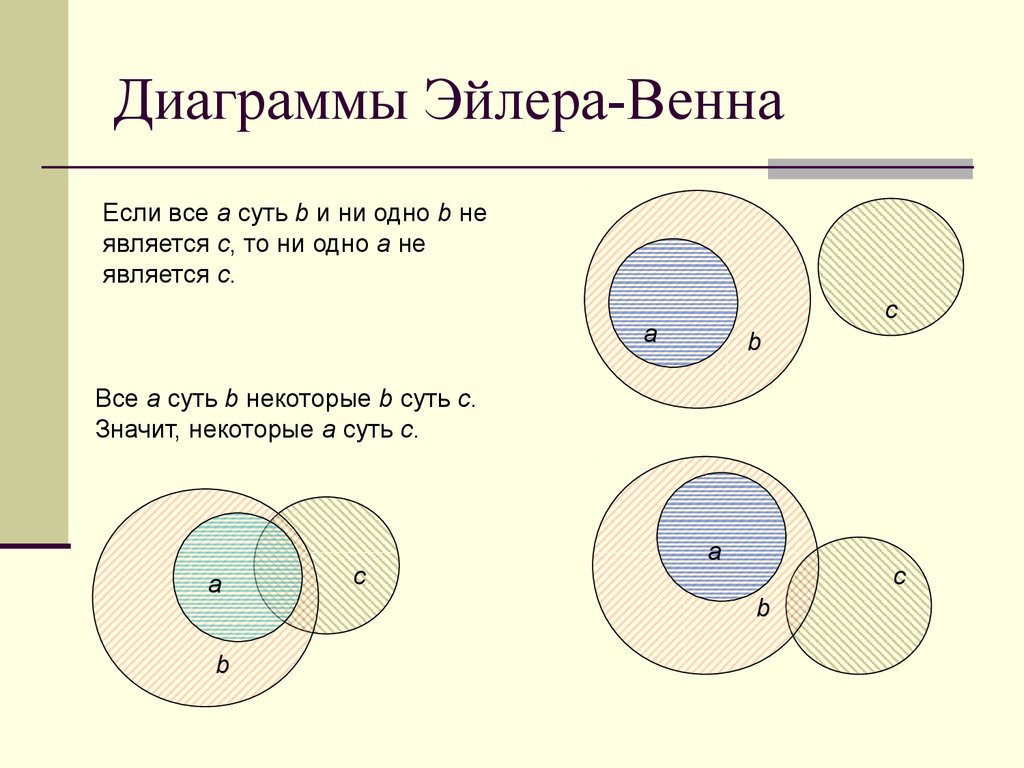

 eulerape <- euler(c("a" = 3491, "b" = 3409, "c" = 3503,
                    "a&b" = 120, "a&c" = 114, "b&c" = 132,
                    "a&b&c" = 126),
                  форма = "эллипс",
                  управление = список (экстраопт = ЛОЖЬ))
plot(eulerape) 

Четыре равномерных взаимодействия

 uniform <- euler(c("A" = 10, "B" = 10, "C" = 10, "D" = 10,
                   "A&B" = 3, "A&C" = 3, "A&D" = 0, "B&C" = 0, "B&D" = 3, "C&D" = 3,
                   "A&B&C" = 1, "A&B&D" = 1, "A&C&D" = 1, "B&C&D" = 1,
                   "А&В&С&D" = 1))
сюжет (униформа, метки = список (метки = c ("Фродо", "Сэм", "Веселый", "Пиппин")),
                            шрифт = 1:4,
                            цвет = 1:4,
                            cex = seq(1, 1.5, length.out = 4))) 

Две окружности, полностью пересекающиеся

 two_overlapping <- euler(c("A" = 0, "B" = 0, "A&B" = 10))
сюжет (два_перекрытия) 

Диаграммы Венна и диаграммы Эйлера с объяснением на примерах

Обновлено: 28 июля 2021 г.

Диаграммы Венна и диаграммы Эйлера выглядят очень похоже, поэтому понятно, что многим людям трудно понять разницу. Хотя оба типа диаграмм основаны на теории множеств, существуют некоторые тонкие различия, которые делают их уникальными. Надеюсь, эта статья рассеет ваши сомнения по поводу диаграмм Венна и диаграмм Эйлера, и я приведу несколько примеров, чтобы было понятнее.

Венн против Эйлера: определение

Как я упоминал ранее, оба набора диаграмм основаны на теории множеств. Диаграмма Венна показывает все возможные логические отношения между наборами множеств. Но диаграмма Эйлера показывает только те отношения, которые существуют в реальном мире.

Диаграммы Венна и

Диаграммы Эйлера Примеры

Начнем с очень простого примера. Давайте рассмотрим надмножество Animals с млекопитающими и птицами в качестве подмножеств. Диаграмма Венна показывает пересечение двух множеств, хотя в реальном мире такой возможности не существует. Диаграмма Эйлера, с другой стороны, не показывает пересечения.

Диаграммы Венна показывают все возможные комбинации, даже если они не существуют в реальном сценарии

Теперь давайте рассмотрим немного более сложный пример с колодой карт. Опять же важно помнить о разнице между двумя типами диаграмм, всеми возможными комбинациями и реальными комбинациями . Возьмем карты как надмножество, а черные карты, красные карты и бубны — как подмножества.

Как одни и те же данные представляются по-разному с использованием диаграмм Венна и диаграмм Эйлера

Как видно из приведенного выше примера, на диаграмме Венна показаны четыре пересечения, для которых нет данных, поскольку они должны отображать все возможные комбинации.

Существуют различные методы преобразования диаграмм Венна в диаграммы Эйлера и наоборот. Посмотрите эту замечательную вики-статью о диаграммах Эйлера, в которой объясняются некоторые методы, которые вы можете использовать для преобразования диаграмм Венна в диаграммы Эйлера.