Читать учебник по математике 3 класс моро: Учебник Математика 3 класс Моро часть 1

Содержание

Страница 61 — ГДЗ по Математике 3 класс Моро, Волкова 2 часть

Тип: ГДЗ, Решебник.
Автор: Моро М. И., Волкова С. И., Бантова М. А.
Год: 2020.
Серия: Школа России (ФГОС).
Издательство: Просвещение.

❤️️Ответ к странице 61. Математика 3 класс учебник 2 часть. Автор: М.И. Моро.

Решебник — страница 61Готовое домашнее задание

Номер 27.

1) Сколько минут составляет третья часть часа? четвертая? пятая? десятая?
2) Рассмотри рисунок. Какие 3 месяца составляют зиму? Назови их. Назови летние месяцы, осенние месяцы.
3) Каждые 3 месяца, начиная с января, называют кварталом. Какие месяцы входят в первый квартал? во второй? в третий? в четвертый? Какую часть года составляет один квартал?

Ответ:

1) 60 : 3 = 20 (мин) 60 : 4 = 15 (мин) 60 : 5 = 12 (мин) 60 : 10 = 6 (мин)

2) Зимние месяцы: декабрь, январь, февраль.

Летние месяцы: июнь, июль, август. Осенние месяцы: сентябрь, октябрь, ноябрь.
3) I квартал – январь, февраль, март. II квартал – апрель, май, июнь. III квартал – июль, август, сентябрь. IV квартал – октябрь, ноябрь, декабрь. Один квартал – это четвертая часть года.

Номер 28.

На вопрос «Который час?» мальчику ответили: «Без четверти три». Он знал, что мультфильмы по телевизору будут показывать в 15.00. Не опоздал ли он?

Ответ:

Время – 14 : 45 – мальчик не опоздал.

Номер 29.

Ответ:

Номер 30.

Сколько всего однозначных чисел? двузначных? трехзначных?

Ответ:

Однозначных чисел – 9. Двузначных – 90. Трёхзначных – 900.

Номер 31.

Найди среди данных записей те, в которых допущена ошибка, выполни вычисления правильно.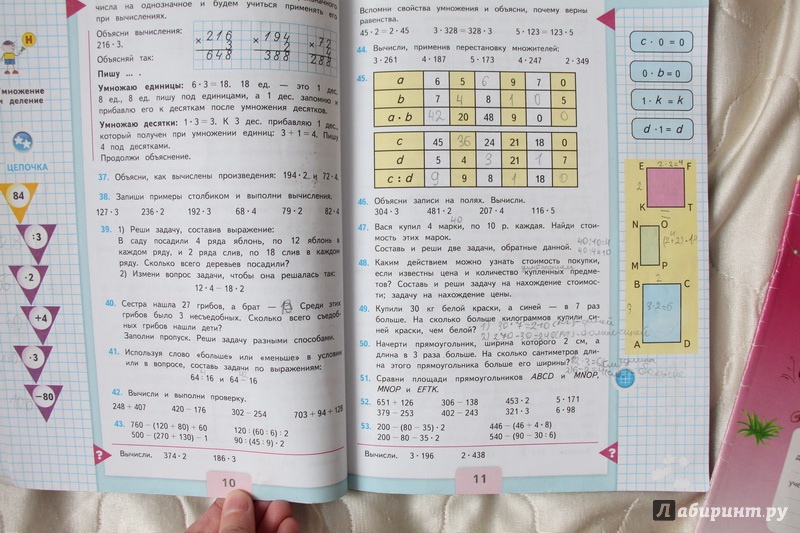

Ответ:

58 : 6 = 9 (ост. 4) 8 : 9 = 0 (ост. 8) 10 : 8 = 1 (ост. 2)

Задание на полях страницы

Начерти и раскрась:

Ответ:

Рейтинг

Выберите другую страницу

1 часть

Учебник Моро	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63	64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79	80	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95	96	97	98	99	100	101	102	103	104	105	106	107	108	109	110	111

2 часть

4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63	64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79	80	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95	96	97	98	99	100	101	102	103	104	105	106	107	108	109	110	111

Математика : 3 кл.

: Учебник : В 2 ч. / Ч. 1 (Александр Чекин)

660 ₽

+ до 99 баллов

Бонусная программа

Итоговая сумма бонусов может отличаться от указанной, если к заказу будут применены скидки.

Купить

Цена на сайте может отличаться от цены в магазинах сети. Внешний вид книги может отличаться от изображения на сайте.

Последний экземпляр

В наличии в 1 магазине. Смотреть на карте

Учебник состоит из двух частей, каждая из которых рассчитана на учебное полугодие. Первая часть посвящена изучению письменной и устной нумерации многозначных чисел и их сравнению, изучению алгоритмов сложения и вычитания столбиком, взаимосвязи умножения и деления, табличных случаев деления, видов треугольников, новых единиц длины и массы.

Большое внимание уделяется решению простых и составных сюжетных задач на все арифметические действия.

Описание

Характеристики

Академкнига

На товар пока нет отзывов

Поделитесь своим мнением раньше всех

Как получить бонусы за отзыв о товаре

Сделайте заказ в интернет-магазине

Напишите развёрнутый отзыв от 300 символов только на то, что вы купили

Дождитесь, пока отзыв опубликуют.

Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя. Можно писать неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в первой десятке.

Правила начисления бонусов

Книга «Математика : 3 кл. : Учебник : В 2 ч. / Ч. 1» есть в наличии в интернет-магазине «Читай-город» по привлекательной цене. Если вы находитесь в Москве, Санкт-Петербурге, Нижнем Новгороде, Казани, Екатеринбурге, Ростове-на-Дону или любом другом регионе России, вы можете оформить заказ на книгу Александр Чекин «Математика : 3 кл. : Учебник : В 2 ч. / Ч. 1» и выбрать удобный способ его получения: самовывоз, доставка курьером или отправка почтой. Чтобы покупать книги вам было ещё приятнее, мы регулярно проводим акции и конкурсы.

You Must Read Building Thinking Classrooms in Mathematics Питер Лильедал

Я работаю преподавателем математики около двадцати лет, и книга Питера Лильедала «Building Thinking Classrooms in Mathematics» обладает большим потенциалом для улучшения методов преподавания математики, чем любая другая книга, которую я когда-либо читал. читать. Это не слова, которые я говорю легкомысленно. Эта книга полностью меняет правила игры для всех преподавателей математики, и каждый должен ее прочитать.

Я пишу этот пост в блоге с двумя целями:

, чтобы убедить вас, почему вы также должны прочитать и применить на практике то, что вы узнали из книги
иметь много глубоких прозрений, которые я отметил в одном месте, чтобы я мог вернуться и прочитать снова

О чем эта книга?

Питер разбил то, что делают учителя математики, на четырнадцать отдельных категорий (называемых практиками). Он хотел проверить, насколько эффективны наши традиционные практики, поэтому он провел эксперименты, чтобы проверить, сколько размышлений происходит, когда учителя используют их. Затем он попросил учителей сделать обратное и сравнил, сколько времени они думают (например, если мы обычно заставляем детей работать сидя, то что произойдет, если они будут работать стоя?). Они продолжали циклы изменения и тестирования альтернатив статус-кво, пока не нашли то, что вызвало больше всего размышлений. В этой книге рассказывается обо всех этих передовых методах, чтобы вы могли применять их со своими учениками. Лучше всего то, что его стиль письма легко читается, в нем нет претенциозности или всезнайки.

Я думаю о каждой практике как о камне бесконечности из фильма Marvel. Вы можете просто использовать один из них, и он сам по себе мощный. Однако чем больше вы комбинируете, тем мощнее он становится.

Какие были четырнадцать практик?

Четырнадцать практик были:

Какие типы задач мы используем
Как мы формируем группы сотрудничества
Где работают студенты
Как мы расставляем мебель
Как мы отвечаем на вопросы учащихся
Когда, где и как даются задания
Как выглядит домашнее задание
Как мы поощряем студенческую автономию
Как мы используем подсказки и расширения
Как мы закрепляем (подводим итоги) урок
Как студенты делают заметки
Что мы выбираем для оценки
Как мы используем формативное оценивание
Как мы оцениваем

Подумайте, насколько обширен этот список. Вероятно, он охватывает не менее 90% того, что мы делаем как преподаватели математики. Если вы уже делаете то, что показало исследование, вы почувствуете себя признанным. Если нет, разве вы не хотели бы знать, что работает лучше всего, чтобы вы могли подумать об изменении?

Теперь я хочу пройтись по частям, которые больше всего меня зацепили. Книга НАПОЛНЕНА удивительными вещами, и мои заметки никоим образом не могут заменить чтение книги. Ниже я цитирую, перефразирую или резюмирую книгу. Практически ничего из этого не является моей интуицией, я просто обрабатываю то, что читаю.

Введение

Питер начинает с определения «мышления» как цели того, что мы хотим, чтобы учащиеся делали на уроках математики, и противопоставляет это тому, что мы часто видим вместо этого на уроках математики, используя классификацию Дэриена Аллана «поведения учащихся». » который включает в себя:

бездельничать – вообще не пытаться работать
зависание — законное поведение, не связанное с работой (например, выпивка или поход в туалет)
притворство – делать вид, что выполняешь задачу, но на самом деле ничего не делать
подражание – бездумное повторение того, что у них есть в заметках
пробовать самостоятельно — пытаться решить проблему, независимо от того, правильно они ее поняли или нет

Я полагаю, что почти каждый учитель сталкивался с таким поведением, но я никогда не видел попытки классифицировать его и нашел категории полезными. Если бы вы спросили меня в начале моей карьеры, о чем думают студенты, я бы наверняка включил в список студентов, которые «пробуют это сделать сами». Впрочем, я, наверное, думал, что «мимикрирующие» ученики тоже думают.

Если честно, я закончил всю среднюю школу и окончил Калифорнийский университет в Лос-Анджелесе со степенью бакалавра. по математике, потому что я был солидным подражателем. Более чем в половине случаев я знал, как получить правильный ответ, но плохо понимал, что делаю. Таким образом, признание того, что подражатели на самом деле не были мыслителями, вынудило бы меня признать, что я тоже не мыслитель, и я, вероятно, не был готов сказать это вслух двадцать лет назад.

Этот отрывок поразил меня прямо под дых: «Когда мы брали интервью у учителей, в классах которых мы проводили исследование учеников, все они подчеркивали, что не хотят, чтобы их ученики подражали. По иронии судьбы, 100% учеников, которые подражали, заявили, что они думали, что подражание было тем, чего хотел от них учитель». Ну блин. Это должно было быть то, что сказал бы я и что подумали бы мои ученики.

Какие типы задач мы используем

Мне очень понравилось, как Питер определил «решение проблем» как «то, что мы делаем, когда не знаем, что делать». Далее он говорит, что «решение проблем — это не точное применение известной процедуры. Это не реализация заученного алгоритма. И это не плавное выполнение формулы. Решение проблем — беспорядочный, нелинейный и своеобразный процесс. Студенты застрянут. Они будут думать. И они отклеятся. И когда они это сделают, они научатся».

Сравните это с тем, как обычно преподают математику: я покажу вам, что нужно делать, а теперь вы практикуете этот навык. Это настолько оторвано от того, что на самом деле происходит в жизни.

Питер описывает три атрибута высококачественных задач по решению проблем:

низкоуровневая задача — любой может приступить к решению проблемы
задача с высоким потолком — они достаточно сложны, чтобы удерживать внимание людей
открытая середина – правильный ответ один, но есть несколько способов решить задачу

Если вы знакомы с моей работой (особенно с Open Middle и моими реальными проблемами), вы не удивитесь, насколько я согласен с этими атрибутами.

Одна часть, которая меня действительно удивила, заключалась в том, что Питер заявил, что проблемы, которые он выбирает, «по большей части все неучебные задачи. То есть очень немногие из этих задач требуют математики, которая хорошо отображается в списке результатов или стандартов в конкретной школьной программе».

Это заставило меня задуматься о том, насколько необходимо было использовать те типы задач, которые он упомянул, и могли ли мы вместо этого найти подходящие замены, которые лучше соответствовали бы стандартам, которые использовали учителя. На самом деле будет трудно заставить учителей выполнять эти практики, если они не привязаны к тому, чему они учат. Я не помню, где в книге он это говорит, но я помню, как Питер упомянул, что когда ученики хорошо думают, все остальное идет быстрее… так что выполнение неучебных задач — это инвестиции, благодаря которым все остальное идет гладко. Далее он рассказывает о том, где взять подобные задачи, а также о том, как превратить существующие проблемы, которые мы используем, в сложные задачи, поэтому я не хочу искажать то, что он говорит.

При этом я предполагаю, что мы могли бы получить аналогичные результаты с тщательно подобранными учебными задачами, такими как Open Middle, и, судя по тому, что я вижу в Твиттере, с этим согласны другие учителя.

@openmiddle + «Класс мышления» @pgliljedahl = отличная вовлеченность студентов во время замечательных вопросов. @JohnDrydenPS @deenickerson16 @Errs5 pic.twitter.com/MhInFc8c3u
— Эл Сэвидж (@TeachMath2618) 3 декабря 2019 г.

Как мы формируем совместные группы

Разделение учащихся на группы происходит постоянно в классах, но я никогда серьезно об этом не задумывался. Например, каково идеальное количество студентов в группе? Как вы решаете, каких студентов объединить в группы? Честно говоря, я не думал, что это имеет большое значение, но исследования показали, что я ошибался.

Эта цитата действительно нашла отклик у меня о том, на что это похоже для студентов в группах: «Подавляющее большинство студентов не входят в свои группы, думая, что они собираются внести значительный вклад, если вообще какой-либо, в свою группу. Они входят в группы в роли последователей, ожидая, что не будут думать. Это означает, что при стратегических группировках, кроме тех 10-20%, которые привыкли брать на себя инициативу, остальные студенты, в общем и целом, знают, что их помещают с некоторыми другими студентами, и живут по эти ожидания».

Именно так и происходит. Большинство детей идут в группу и сидят там, ожидая, пока кто-то другой возьмет на себя инициативу и успеет пройти время. Это одновременно не удивляет ни одного учителя и совсем не то, чего мы хотим, когда ученики находятся в группах. Итак, как мы обойдем это?

В его предложениях было много нюансов, но вот два резюме:

Группы должны были быть явно случайными. Каждый студент будет думать, что вы намеренно помещаете его в группу, независимо от того, насколько случайным вы называете это. Единственный способ обойти это — сделать его явно и бесспорно случайным. Например, есть веб-сайты, подобные этому, и бесчисленное множество других, где вы можете вводить имена, и он будет генерировать для вас группы. Это также можно сделать с помощью офлайн-методов, таких как колода карт. Я бы и не догадался, насколько важно визуально рандомизировать группы, чтобы разрушить представление студентов о том, что они были помещены в группу по определенной причине, которая делает их более открытыми для реального участия.
Три ученика — идеальный размер группы. Он говорит: «Группы из двух человек боролись больше, чем группы из трех, а группы из четырех человек почти всегда превращались в группу из трех плюс один или две группы из двух». Ну, это легко реализовать, и я понятия не имел. Я почти всегда делал группы из четырех человек.

Где работают студенты

Возможно, об этой практике я думал меньше всего. По сути, вся моя жизнь, когда я был студентом-математиком, провела за письменным столом. Я не думаю, что мне когда-либо приходило в голову, что мы могли бы заниматься математикой где-то еще, так что это то, что делает результаты исследования Питера о том, где студенты работают, намного более глубокими.

Проще говоря, когда наши группы из трех студентов пишут на вертикальной поверхности, например, на белой доске или бумаге для плакатов, они развивают гораздо больше мышления, чем когда они работают, сидя за партой. Его результаты гораздо более тонкие, чем я описываю, включая то, кто использует маркер для письма, кто использует какой цвет, что можно стереть и т. д. Например, я, вероятно, дал бы каждому ученику свой собственный маркер, но исследование показало что «когда у каждого члена группы есть свой собственный маркер, группа быстро превращается в трех человек, работающих параллельно, а не сотрудничающих».

Конечно, это потребует некоторых изменений в том, как мы обустраиваем наши классы, но если это значительно улучшит мышление, я согласен.

Как мы расставляем мебель в том, что сам бы никогда не додумался до этого, но сразу после прочтения было очевидно, что он прав. Например, представьте, что вы входите в большую аудиторию на лекцию в колледже. То, как была обставлена эта комната, дало нам понять, что в ней не будет много групповой работы и разговоров. Наша роль заключалась в том, чтобы слушать всех, кто был на подиуме.

Итак, мой вопрос к вам: как бы вы разместили учеников в классе, чтобы показать, будут ли они думать или НЕ будут думать? Возможно, ряды парт, обращенные к передней части класса, будут ближе всего к лекции и означают, что здесь слушание важнее, чем сотрудничество. Итак, как бы вы изменили класс, чтобы показать обратное?

В конечном счете, Питер обнаружил, что учителям «нужно было убрать фасад комнаты только для того, чтобы выпрямить и десимметризовать ее, если мы определяли удаление фасада как обеспечение того, чтобы каждый стул в комнате был обращен в разные стороны компаса». Причина в том, что, когда есть перед классом, оттуда приходят знания. Учитель, как правило, находится впереди класса, поэтому сообщение, которое мы передаем, заключается в том, что учитель — это источник знаний. Дефолт в классе устраняет это невысказанное ожидание.

Вот пример того, как это может выглядеть:

✅Осквернение класса!
Погружение в реализацию #thinkingclassroom в 8 классе по математике. Спасибо @pgliljedahl за вдохновение!
Несмотря на то, что уже конец дня, комната готова!
✅Доски (VNPS)
✅Видимые рандомизированные группы
✅Открытые вопросы среднего мышления. pic.twitter.com/sR50XIbanh
— Джон Стивенс (@CTEPEI) 22 марта 2022 г.

Понравится ли моим склонностям к ОКР дефронтный класс? Не изначально. Стоит ли оно того, если оно заставит детей задуматься? Да, черт возьми.

Этот абзац действительно потряс меня, потому что он показал нереализованный недостаток, который я имел обыкновение делать: «Мышление беспорядочно. Это требует значительного риска, проб и ошибок и нелинейного мышления. Оказывается, в суперорганизованных классах учащиеся не чувствуют себя в безопасности, чтобы запутаться таким образом. Сообщение, которое они получают, заключается в том, что обучение должно быть упорядоченным, структурированным и точным». Вместо прямых и симметричных классов, помогающих ученикам, они возлагали невысказанные ожидания на мышление, которое поощрялось в этом классе. Проклятие. Если бы я только знал, что мои усилия имели такой эффект.

Как мы отвечаем на вопросы учащихся

Эта глава во многом напомнила мне мою метафору о жиме лежа и ассистенте: цель ассистента — оказать жиму лежа наименьшую помощь, необходимую для поднятия веса. Точно так же наша цель как учителей состоит не в том, чтобы отвечать на вопросы каждого ученика. Вместо этого нам нужно стратегически подходить к вопросам, на которые мы отвечаем.

Первым большим открытием для меня стала его классификация типов вопросов, которые задают студенты. Он пишет: «Как оказалось, учащиеся задают только три типа вопросов: вопросы на близость, вопросы на остановку и вопросы на продолжение». Он очень хорошо разбивает эти категории, но грубое объяснение таково:

Вопросы близости — это те, которые учащиеся обычно задают, только когда вы находитесь рядом с ними, и обычно они не так важны
вопросов на прекращение мышления — это вопросы, на которые дети не хотят думать, и они просят что-то, чтобы либо заставить вас думать за них, либо дать им разрешение полностью перестать думать.
вопросов, побуждающих к размышлению, — это те вопросы, которые действительно помогают продолжить размышления

Далее он рассказывает, как «оказывается, что из 200-400 вопросов, на которые учителя отвечают в день, 90% — это комбинация вопросов на остановку и близость». Затем он продолжает, говоря: «Ответы на эти вопросы о близости или остановке мышления противоречат построению мыслящего класса. Единственные вопросы, на которые следует отвечать в думающем классе, — это небольшой процент (10%) вопросов, направленных на постоянное обдумывание».

Хотя это и имеет смысл, я уверен, что ответил на вопросы о близости и остановке мышления гораздо чаще, чем должен был. Он продолжает делиться отличными идеями, как избежать ответов на неправильные вопросы, в том числе о том, как избежать восстания студентов из-за того, что вы недостаточно полезны.

Когда, где и как даются задания

Исследование показывает, что мы даем задания учащимся как можно быстрее (а не позже в классе), и что мы делаем это, сгрудившись вокруг центральной области, а не чем сидеть на своих местах.

То, что поразило меня и по-прежнему трудно принять, это то, что исследование показало, что это лучший способ дать ученикам задание. Так что можно подыгрывать, ранжировать эти способы выдачи ученикам задания от наиболее до наименее эффективных.

Проектирование задачи
Предоставление предварительно напечатанного
Запись на доске
Устно

Я не знаю, какой приказ вы выбрали, но я точно знал, что отдать его в устной форме будет последним. Поэтому меня еще больше шокировало, когда я прочитал: «Ничто не было так эффективно, как устное задание. Это был шокирующий результат. Это не только противоречит десятилетним нормам, но и противоречит инстинктам учителей».

ЧТО?!

Теперь я должен абсолютно точно уточнить, что он вдается в мельчайшие детали и поясняет, что значит давать задание в устной форме, в том числе говорит, что «устные инструкции — это не зачитывание задания дословно». И дает великое множество практических советов по реализации. Но, как он написал, это идет вразрез с моими инстинктами, и я все еще пытаюсь это переварить.

Как выглядит домашняя работа

Реальность для большинства классов такова, что домашняя работа бесполезна для большинства учащихся. Питер классифицирует опыт большинства учащихся с домашним заданием как то, что они либо не сделали его, либо получили помощь, либо смошенничали, либо пытались сделать это самостоятельно. Из тех, кто делал это самостоятельно, «подавляющее большинство выполнили домашнее задание, подражая либо своим заметкам, либо учебнику».

Соответственно, домашняя работа дает очень мало реальных мыслей. Он поделился, что «данные о домашних заданиях показали, что 75% учащихся выполнили домашнее задание, и только около 10% делали это по уважительной причине. Когда целью является завершение, оно поощряет, а иногда и вознаграждает такое поведение, как обман, подражание и получение бесполезной помощи».

Так что же нам делать? Питер предполагает, что решение состоит в том, чтобы переключить домашние задания с учителей на их собственное обучение. Чтобы сделать этот переход, они «перестали называть это домашним заданием и начали называть это вопросами для проверки вашего понимания». Это в сочетании с несколькими другими изменениями, в том числе: отказ от выставления оценок за домашнее задание, отказ от наказания детей за их невыполнение и т. д., привело к значительному улучшению мышления. Я не отдаю должное многочисленным советам, основанным на исследованиях, которые он предлагает, но эта глава великолепна.

Помните, что с нашими существующими методами они уже не работают. Таким образом, хотя этот новый подход может сильно отличаться от нашего собственного опыта, лучше, чтобы некоторые студенты действительно думали, чем большинство студентов, которые практически ничего не делают.

Как мы развиваем автономию учащихся

Вы, наверное, были в классе, где дети прячут свою работу и ответы друг от друга, чтобы никто их не обманул. Неудивительно, что в этом классе, вероятно, не так много сотрудничества.

Итак, Питер предлагает стратегии, которые помогают учащимся контролировать свое обучение, а не полагаться на вас как на источник всех своих знаний. Стратегии, казалось, подтверждали то, что я уже делал, и большинство из них казались довольно интуитивными.

Как мы используем подсказки и расширения

Эта глава была одновременно интуитивно понятной и казалась тем, что я мог бы посвятить остаток своей карьеры попыткам стать лучше. Позволь мне объяснить.

Вы когда-нибудь были в зоне, где вы были настолько увлечены чем-то, что делали, что все остальное вокруг вас как бы исчезало? Некоторые люди называют это «потоком». Хорошо представьте, что происходит на уроке математики, когда ученики настолько увлечены тем, над чем они работают, что попадают в зону.

Во-первых, их будет трудно доставить туда с самого начала, но также будет трудно и удержать их там. Если это будет слишком просто или скучно, они выпадут. Если это слишком сложно или запутанно, они выпадут. Вычисление нужного количества требует большого мастерства. Он подробно описывает как теорию, стоящую за этим, так и практические советы, как удержать своих учеников в зоне.

Мне очень нравится эта цитата, которой он поделился: «Цель создания думающих классов не в том, чтобы найти интересные задачи для размышлений учеников. Цель думающих классов — воспитать вовлеченных учащихся, готовых обдумывать любую задачу». Такой простой, но такой глубокий сдвиг.

Как мы объединяем (подводим итоги) Урок

Я все еще обрабатываю эту главу, чтобы объединить ее с тем, что я уже знал. В частности, я большой поклонник «5 практик организации продуктивных математических дискуссий» Пег Смит и Мэри Кей Стейн. Фактически, Thinking Classrooms и 5 Practices, вероятно, две книги, которые больше всего повлияли на меня как на преподавателя математики. Итак, я пытаюсь осмыслить контраст, который он предлагает.

Он говорит: «В то время как Смит и Штейн выполняют и выбор, и последовательность в данный момент, в мыслящем классе последовательность уже определена на этапе создания задачи — создана для запуска и поддержания потока. Осталось выбрать студенческую работу, которая иллюстрирует математику на разных этапах этой последовательности».

Я понимаю, что он говорит, но я бы возразил и сказал, что большинство учителей, использующих 5 практик, уже имеют представление о том, какую работу ученики они надеются найти, и в каком порядке они надеются поделиться ею перед уроком. . Затем они ходят по комнате в надежде найти это или подтолкнуть студентов в этом направлении. Так что в этом отношении я думаю, что это довольно похоже.

При этом Питер также упоминает, что «еще одно отличие состоит в том, что, в то время как Смит и Штейн заставляют студентов представлять свои собственные работы, в классе мышления расшифровка работы студентов предоставляется остальным в комнате». Это интересно, потому что это лежит в основе того, что происходит, когда ученик выступает перед классом. Все проверены? Они помолвлены? Как вам это удается?

Он распаковывает лучше, чем я, но если вы поклонник Смита и Штейна, я думаю, эта глава вам понравится еще больше.

Как учащиеся делают заметки

Если бы мне нужно было использовать одну картинку, чтобы обобщить, каково это делать заметки на уроке математики, я бы выбрал вот эту:

Лично я редко делаю заметки, потому что, когда я это делаю, Я изо всех сил пытаюсь обработать сказанное в режиме реального времени, и, честно говоря, я почти никогда не просматриваю свои записи, так зачем беспокоиться? Я сомневаюсь, что что-то из этого шокирует вас, поэтому вопрос в том, что если мы все согласны с тем, что статус-кво для ведения заметок не очень хорош, каковы наши альтернативы?

То, что придумал Питер, прекрасно в своей простоте: они писали «записки себе в будущее забывчивым». Они спросили студентов: «Что вы собираетесь записать сейчас, чтобы через три недели вспомнить то, что вы узнали сегодня?»

Он также экспериментировал со всевозможными графическими органайзерами, которые делали заметки более управляемыми и менее громоздкими. Было бесчисленное множество вещей, великолепие которых было очевидно только после того, как он это описал, потому что я никогда не собирался рассматривать и изучать это самостоятельно. Это определенно тот раздел, в который стоит погрузиться.

Что мы выбираем для оценки? ни к чему из написанного? Я предполагаю, что у вас есть.

Выбрать, какую работу оценивать и как ее оценивать, чтобы учащиеся действительно росли на этом опыте, непросто. Иногда это терпит неудачу, потому что мы пытаемся относиться к ней как к формирующей, так и к итоговой оценке одновременно… и это не особенно хорошо. Иногда это терпит неудачу, потому что способ, которым мы передаем обратную связь, не воспринимается так, как мы хотели.

Чтобы бороться с этими реалиями, Питер делится множеством пересмотренных рубрик, которые мы можем использовать, чтобы помочь учащимся задуматься о своем прогрессе. Я особенно ценил детальную разбивку стратегий, которые они пробовали, но пересматривали по ходу дела. Это помогает не только увидеть, какой вариант был лучшим, но и некоторые шаги на пути к нему. Например, вместо рубрики, в которой каждый столбец имел бы дескриптор, вы могли бы иметь дескрипторы в начале и в конце, но со стрелкой, указывающей в направлении роста. Это помогло учащимся перейти от восприятия того, где они находятся, к восприятию того, где они находятся, как к указателю на пути.

Как мы используем формативное оценивание

Эта глава также полна очень интересных идей, помогающих учителям собирать информацию в режиме реального времени, которую они могут немедленно использовать для корректировки своего обучения. Хотя было много стратегий, которые вы могли бы использовать, я поделюсь одной, которую никогда не слышал, но сразу полюбил.

Он написал: «В конце учебного блока попросите вашего студента сделать контрольный тест, по которому он получит 100%. Если они могут это сделать, значит, они знают то, что знают. Затем попросите их сделать контрольный тест, за который они получат 50%. Если они смогут это сделать, то они будут знать то, что знают и знают то, чего не знают». Это увлекательно! Я никогда не пробовал это со студентами, но мне так любопытно, как они отреагируют.

Как мы выставляем оценки

Вы когда-нибудь задумывались о том, насколько субъективна оценка? Например, при подсчете среднего балла A составляет 4 балла, а F — 0 баллов. Таким образом, если человек получает A и F, он имеет в среднем 2 балла, что соответствует C. С процентами, если кто-то получает A (100%) и F (0%), это в среднем составляет 50%, что составляет Ф!

Когда одни и те же баллы могут дать разные итоговые оценки, что-то не так. Еще более сложной задачей является то, что оценки учащихся могут не отражать того, что они знают. Часто учитываются такие вещи, как участие и домашнее задание, что может привести к тому, что оценка исказит их знания.

Например, рассмотрим этих учащихся, которые в конце года получают одинаковую оценку C:

Каждый начинает год со всеми пятерками и заканчивает год со всеми пятерками
Каждый получает тройку за каждое задание
Год начинается со всех F и заканчивается годом со всеми As

Что вы думаете о том, где находится каждый ученик? Соответствует ли каждая из их оценок C тому, что они демонстрируют в настоящее время? Хотя это мои примеры, Питер делает то же самое, говоря о том, что традиционного способа оценивания учеников не хватает, и стоит подумать о лучших вариантах.

Питер выступает за переход от сбора точек к дискретным точкам данных, которые больше не привязывают учащихся к тому, откуда они пришли, а более точно показывают, где они находятся в настоящее время. Есть много преимуществ, но, пожалуй, больше всего мне нравится то, что учителя и ученики получают представление о том, где находится ребенок, и побуждают их всегда продолжать учиться, а не сдаваться, когда кажется, что улучшение их оценок безнадежно.

Объединение 14 практик

Питер завершает книгу, делясь своими выводами на вопрос «Как лучше всего применять эти 14 практик, или порядок не имеет значения?» Он пришел к выводу, что группировка практик в четыре «инструментария» дает учителю вехи, когда они должны сосредоточиться на одном наборе практик, прежде чем переходить к другому. Он даже доходит до того, что рассказывает, в каком порядке их выполнять после первого года обучения, когда они станут для вас более знакомыми.

Заключение

Надеюсь, вам понравились мои размышления о книге Питера. Я хотел бы прочитать о том, что нашло отклик у вас в комментариях, и я был бы особенно признателен вам за то, что вы подтолкнули меня к любым вопросам, которые я, возможно, не полностью обрабатываю.

Я должен добавить, что одна часть, о которой я не упомянул, заключается в том, что каждая глава заканчивается FAQ с вопросами, которые Питер часто получает о практиках, а также вопросами, о которых вы можете поговорить в изучении книги или самостоятельно. Даже если у меня не было собственных вопросов после прочтения о практике, я ценил то, что задавали другие, потому что они часто были довольно хорошими.

Лучшие детские книги для раннего обучения математике

Один из верных способов подогреть отношение детей к математике — строить математические задания и уроки из книг, которые они все любят слушать и читать.

Дети изучают основные идеи фундаментальных математических понятий, взаимодействуя с математикой в повседневной жизни. При чтении и прослушивании книг математические ситуации оживают новым и причудливым образом. И мы говорим не только о книгах, которые явно математические, поскольку математика часто занимает центральное место в проблеме и решении наших любимых историй. Так много вопросов, которые волнуют детей, таких как «Справедливо ли это?», «Кто больше/быстрее/сильнее?», «Что будет дальше?» разделяют персонажи, о которых они читают.

Но не забудьте вычеркнуть математику из учебника! Играйте с историями. Разыграйте их и внесите новшества. Задайте вопросы «что, если». Создайте свою версию. Здесь математическое мышление становится творческим.

Мы собрали множество списков и идей для занятий, связанных с некоторыми из лучших известных нам детских книг, и все они пронизаны математическими понятиями. Мы наметили ссылки ниже, организованные по ранним математическим темам нашего веб-сайта. Используйте математические книги для детей, чтобы показать им, как воплотить математику в жизнь!

Где математика? Книги, игры и упражнения для развития мышления у детей

Сделайте изучение математики осмысленным и увлекательным, опираясь на детское любопытство, чтобы помочь им вырасти уверенными в решении задач и исследователями математических концепций.
Узнать больше ›

Наборы

Наборы являются основой для мышления и обучения детей. Они также являются основой нашей системы счисления. Книги о множествах и сортировке могут быть разнообразными и проникать в суть фундаментальной математики. еще

книги для дошкольников | книги для детского сада | Учебники для 1-го класса

Карточки для занятий дома

Чувство чисел

Чувство числа — это способность понимать количество набора и имя, связанное с этим количеством. Переход от этого врожденного, неформального знания чисел к общепринятому пониманию смысла чисел представляет собой важное когнитивное развитие, которое происходит постепенно.подробнее

учебники для дошкольников | книги для детского сада | Учебники для 1 класса | учебники для 2 класса | Учебники для 3-го класса

Счет

Счет является частью повседневной жизни маленьких детей, так же как и книги, которые они слушают. Они любят считать все, от лестницы, по которой они поднимаются, до крекеров, которые они едят. подробнее

Карточки с домашними заданиями

Операции

Когда дети сосредотачиваются на том, что происходит, когда мы соединяем два набора вместе или разделяем набор на части, они узнают, как меняется количество. Когда у них будет большой опыт сравнения сумм, они привыкнут думать о различиях между наборами. подробнее

Балансирующий акт Эллен Столл Уолш | Цветная ферма Лоис Элерт | я знаю старушку, которая проглотила муху Мэри Энн Хоберман | Один — улитка, десять — краб by April Pulley Sayre | Комната на метле Джулии Дональдсон и Акселя Шеффлера | Rooster’s Off to See the World Эрик Карл | звонок в дверь по Pat Hutchins | слишком много тамалес по Gary Soto | Двенадцать способов добраться до одиннадцати Евы Мерриам | Когда линия изгибается… Форма начинается, Ронда Гоулер Грин

учебники для дошкольников | книги для детского сада | Учебники для 1 класса | учебники для 2 класса | Учебники для 3-х классов

Образец

Образец — это не столько тема математики, сколько определяющее качество самой математики. Математика «имеет смысл», потому что ее закономерности позволяют нам обобщать наше понимание от одной ситуации к другой. подробнее

учебники для дошкольников | книги для детского сада | Учебники для 1-го класса

Измерение

Измерение — это любой процесс, который дает количественное описание атрибута, такого как длина, окружность, вес, температура, объем или число. Измерение — это, по сути, математическая процедура, которую мы применяем во многих различных контекстах. подробнее

Анализ данных

Анализ данных может быть очень простым, например, составить список элементов и написать, сколько у вас есть каждого из них в скобках, или создать и обсудить гистограмму, столбцы которой выше для снежных, чем дождливых дней в январе месяце. подробнее

учебники для дошкольников | книги для детского сада | Учебники для 1-го класса

Пространственные отношения

Дети в возрасте от 3 до 6 лет более чем готовы развивать свои навыки выражения направлений из разных мест и понимания относительного положения. Книги по математике для детей могут стать началом большого исследования. подробнее

учебники для дошкольников | книги для детского сада | Учебники для 1 класса | учебники для 2 класса | Учебники для третьего класса

Форма

Все в материальном мире имеет форму. В математике большое внимание уделяется правильным формам, таким как двумерный круг, треугольник и прямоугольник, а также трехмерным телам, известным как сферы и многогранники. подробнее

Карточки для занятий дома: Shape

Большие идеи ранней математики:

Что нужно знать учителям маленьких детей

Основные идеи, передающие основные концепции математики, лежат в основе этой книги, которая дает воспитателям дошкольных учреждений навыки, необходимые им для организации преподавания математики.

Читать учебник по математике 3 класс моро: Учебник Математика 3 класс Моро часть 1

Страница 61 — ГДЗ по Математике 3 класс Моро, Волкова 2 часть

Математика : 3 кл.

Как получить бонусы за отзыв о товаре

You Must Read Building Thinking Classrooms in Mathematics Питер Лильедал

Лучшие детские книги для раннего обучения математике

Где математика? Книги, игры и упражнения для развития мышления у детей

Наборы

Чувство чисел

Счет

Операции

Образец

Измерение

Анализ данных

Пространственные отношения

Форма

Большие идеи ранней математики:

Что нужно знать учителям маленьких детей

Добавить комментарий Отменить ответ

Рубрики