Страница 45. Урок 17 — ГДЗ Математика 2 класс. Петерсон. Учебник часть 2
- Главная
- ГДЗ
- 2 класс
- Математика
- Петерсон. Учебник часть 2
- Страница 45. Урок 17
Вернуться к содержанию учебника
Вопрос
Задание № 7. Площадь трёх комнат равна 44 м2. Площадь первой комнаты составляет 24 м2, площадь второй комнаты — 8 м2. Чему равна площадь третьей комнаты? Реши задачу двумя способами.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
Задание № 8. Найди значения выражений:
| 35 — (17 — 9) + (54 — 6) | |
| (90 — 52) + 14 — (15 + 37) | 912 — (246 + 589) + 478 |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
Задание № 9.
Составь по схемам выражения и найди их значения.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
Задание № 10. Сравни и сделай запись в тетради, используя знаки <, >, =:
| 3 м 29 дм | 270 см 2 м 7 дм |
| 43 дм 3 м 4 дм | 4 м 7 дм 48 см |
| 5 м 4 см 540 см | 4 дм 7 см 47 см |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
Задание № 11. Начерти прямоугольник, длина которого равна 6 см, а ширина на 2 см меньше. Найди его периметр.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
Задание № 12.
Игра «Вычислительные машины»
Вычисли по заданному алгоритму значения х, расположи их в порядке убывания и расшифруй фамилию известного писателя-сказочника.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
Задание № 13. Продолжи ряд на 4 числа: 2, 7, 4, 14, 6, 21, 8, 28 …
Ответ
Поделись с друзьями в социальных сетях:
Вернуться к содержанию учебника
ГДЗ по математике, 2 класс, Моро М.И. «Магические квадраты» – Рамблер/класс
ГДЗ по математике, 2 класс, Моро М.И. «Магические квадраты» – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
Сложи числа в каждом квадрате по строкам, по столбцам, из угла в угол.
Если суммы равны, то такой квадрат называется магическим.
ответы
Сумма чисел по строкам, по столбцам и с угла на угол в
голубом квадрате равна 15, а в розовом — 12.
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
3 класс
5 класс
Репетитор
Химия
похожие вопросы 5
ГДЗ по математике, 2 класс, Моро М.И. Разбей все разности на две группы.
Разбей все разности на две группы.
90-50 80-60 30-10 70-30
60-20 50-30 90-70 40-20 (Подробнее…)
ГДЗМатематика2 классМоро М.И.
ГДЗ по математике, 2 класс, Моро М.И. Заполни таблицу
Кто сделал уже? (Подробнее…)
ГДЗМатематика2 классМоро М.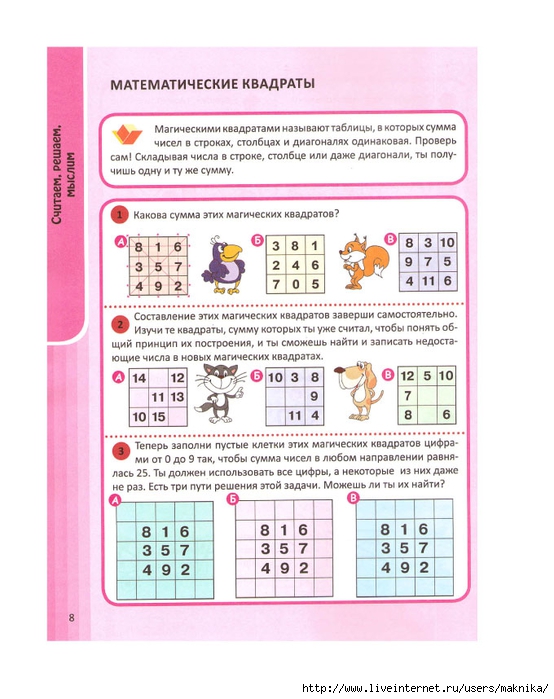
И.
Значение выражения. ГДЗ Математика 6 класс Чесноков. Дидактические материалы по математике для 6 класса. Вар.1 Вопр.259
Кто выполнит? Найдите значение выражения:
ГДЗМатематика6 классЧесноков А.С.
Привет! Помогите определить вес мальчика. № 188. ГДЗ Физика 10 класс Рымкевич.
Определить вес мальчика массой 40 кг в положении А и В (рис. 51), если R1 = 20 м, v1= 10 м/с, R2 = 10 м, v2 = 5 м/с.
(Подробнее…)
ГДЗФизика10 классРымкевич А.П.
370. На прямой даны три точки Л, Я и С, причём АВ= 13см, АС = 4 см. Найдите длину отрезка ВС. 5 класс Математика Никольский С.М.
370.
На прямой даны три точки Л, Я и С, причём АВ= 13см, АС = 4 см. Найдите длину отрезка ВС. (Задача имеет два решения.)
ГДЗМатематика5 классНикольский С.М.
Головоломки с магическими квадратами
Магические квадраты — это одна из самых простых форм логических головоломок и отличное введение в методы решения задач, выходящие за рамки традиционных арифметических алгоритмов.
Каждый квадрат разделен на ячейки, и правила требуют, чтобы сумма любой строки, столбца или диагонали в квадрате была одинаковой. Учитывая магический квадрат с пустыми ячейками, ваша задача состоит в том, чтобы решить головоломку, вставляя недостающие числа. На этой странице есть рабочие листы магических квадратов 3×3, 4×4 и 5×5, которые подготовят вас к другим задачам, таким как печатные головоломки судоку и многое другое!
3×3 Головоломки с магическим квадратом
16 Головоломки с магическим квадратом
Магические квадраты 3×3 на этих листах головоломок представляют собой наименее сложную форму магических квадратов, которую вы можете решить. Существуют нормальные версии (с номерами 1-9) и ненормальные версии, которые при решении дают другое «магическое число». Попробуйте их, прежде чем перейти к магическим квадратам 4×4!
3×3 Magic Square
4×4 Magic Square Puzzles
48 Magic Square Puzzles
Эти более сложные магические квадраты 4×4 являются шагом вперед по сравнению с головоломками 3×3, но все еще довольно легко решаются, если вы тренировались в своих листах сложения.
Обычные квадраты со значениями от 1 до 16 решить легко, но для ненормальных квадратов может понадобиться калькулятор!
Магический квадрат 4×4
Головоломки 5×5 с магическим квадратом
48 Головоломки с магическим квадратом
Обычные магические квадраты 5×5 имеют числа от 1 до 25 и могут быть настоящей головоломкой. Необычные версии головоломок 5×5 — отличные упражнения для детей (или взрослых!), у которых есть хорошие навыки решения проблем.
Магический квадрат 5×5
Головоломки 6×6 Магический квадрат
48 Головоломки магический квадрат
Эти рабочие листы начинаются с обычных магических квадратов 6×6 с числами от 1 до 36, но ненормальные версии головоломок 6×6 чрезвычайно сложны для решения и, вероятно, потребуется ваш калькулятор и некоторое время.
Волшебный квадрат 6×6
Попробуйте эти распечатанные листы-головоломки с волшебным квадратом!
Головоломки с магическим квадратом — один из самых ранних типов головоломок с числами, датируемый 6-м или 7-м веком до нашей эры.
Мы находим ранние записи головоломок с магическими квадратами из Китая и Аравии.
Другие типы головоломок, включая судоку, требуют аналогичных навыков для решения, что делает головоломки с магическим квадратом хорошим введением в более широкий класс логических головоломок с пропущенными числами.
Магический квадрат обладает тем свойством, что сумма чисел в каждой строке является одним и тем же значением, а также сумма чисел в каждом столбце является одним и тем же значением, а также сумма двух диагоналей является одним и тем же значением. При решении головоломки с магическим квадратом некоторые ячейки будут пустыми, и ваша задача состоит в том, чтобы выяснить, какие числа входят в эти ячейки, чтобы сделать все суммы строк, столбцов и диагоналей равными.
Нормальные магические квадраты и ненормальные магические квадраты
Магический квадрат считается «нормальным», если он содержит числа, которые являются наименьшими возможными значениями. Например, магический квадрат 3×3 состоит из девяти ячеек, а обычный магический квадрат 3×3 будет содержать только числа от 1 до 9.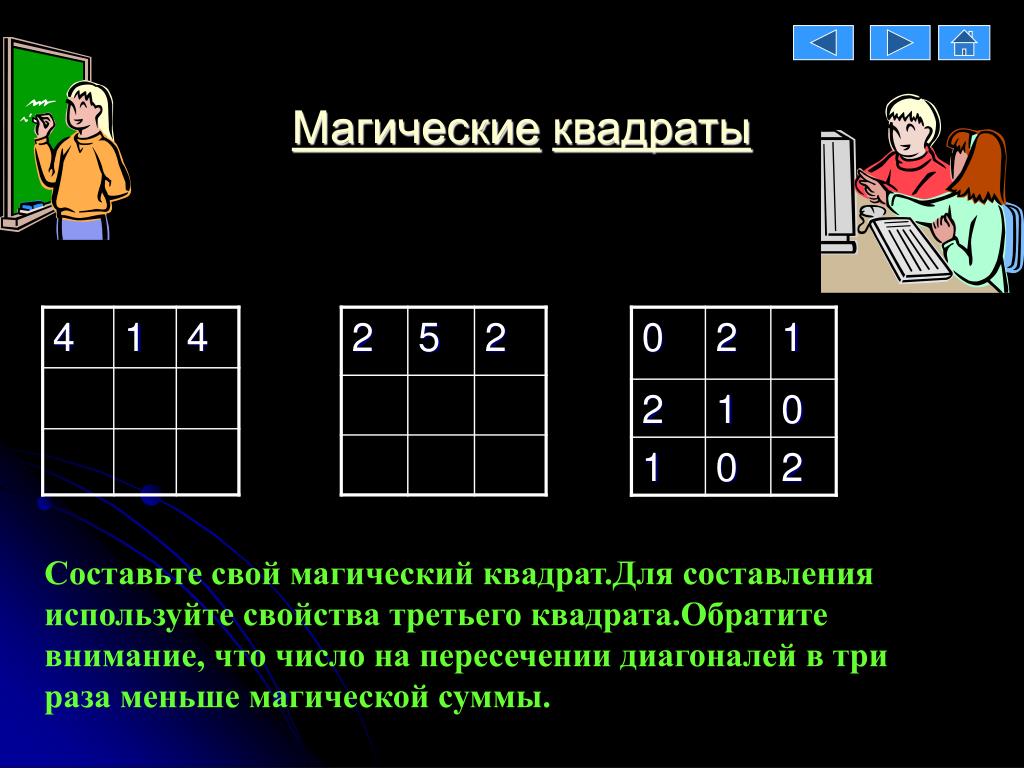
Точно так же магический квадрат 4×4 с 16 ячейками содержит только значения от 1 до 16, а магический квадрат 5×5 содержит только значения от 1 до 25.
Ненормальный квадрат не использует минимальные числа в своих ячейках, поэтому суммы строки, столбцы и диагонали могут быть больше.
Что такое Орден Магического Квадрата?
Заказать для измерения магического квадрата по горизонтальной и вертикальной оси квадрата. Поскольку он квадратный, эти значения для данной головоломки одинаковы. Например, для магического квадрата 3×3 мы говорим, что это магический квадрат «3-го порядка». Магический квадрат 4×4 — это 4-й порядок, 5×5 — 5-й порядок и так далее.
Что такое магическая константа для магического квадрата?
Магическая константа — это значение, которое вы получаете для каждой строки, столбца или диагональной суммы в магическом квадрате. Любопытным свойством обычного магического квадрата является то, что магическая константа для нормального магического квадрата заданного порядка всегда одна и та же.
Магическая константа для нормального магического квадрата 3-го порядка (магический квадрат 3×3) всегда будет равна 15. Точно так же обычные магические квадраты 4-го порядка всегда будут иметь магическую константу 34, нормальные магические квадраты 5-го порядка будут иметь константу 34. Обычные магические квадраты 65 и порядка 6 будут иметь магическую константу 111. Эти константы пригодятся здесь при решении головоломок с обычными магическими квадратами!
Вы можете узнать НАМНОГО больше о магических квадратах, посетив https://www.grogono.com/magic/index.php 92 последовательных чисел, где все столбцы, строки и диагонали в сумме дают одно и то же «волшебное» число? Вы можете посмотреть видео ниже для более подробного объяснения.
Решение квадрата 3 на 3
Сетка 3 на 3 не доставила мне особых хлопот, и вот почему.
- Немного подумав, я обнаружил, что существует простой способ найти «магическое число» сетки любого размера: взять сумму всех чисел на доске и разделить ее на количество строк.
В данном случае магическое число 1+2+…+9= 45 / 3 = 15. - Становится очевидным, что «среднее», самое нейтральное число, 5, лучше всего работает в середине сетки из соображений баланса; более низкие и более высокие числа хорошо работают на противоположных сторонах или углах, но было бы почти невозможно сбалансировать сетку, скажем, с 1 в середине.
- После этого я просто немного поиграл с числами (используя Google Таблицы, чтобы избежать утомительных ручных вычислений) и довольно быстро нашел решение.
В данном случае магическое число 1+2+…+9= 45 / 3 = 15.Решение квадрата 4 на 4 (долгий путь к короткому ответу)
Изучая решение 3 на 3, я начал замечать закономерности. Во-первых, я мог видеть, что если я разобью числа на группы (1–3, 4–6, 7–9), я сбалансирую сетку, гарантируя, что ни одно число из одной и той же группы не разделит строку или столбец. Также казалось наиболее выгодным иметь среднее число в середине, потому что мне еще предстояло найти решение, которое не помещало бы 5 в средний квадрат.
Но с сеткой 4 на 4 середины нет… так как же это будет работать?
Временно игнорируя это, моей первоначальной идеей было рассматривать каждую группу чисел как отдельный цвет и настроить сетку 4 на 4 так, чтобы никакие два поля одного цвета не пересекались в строке или столбце, просто чтобы упростить процесс, который я использовал для 3-на-3. Я подумал, что, найдя эту сетку, я могу поменять местами числа в каждой группе между ячейками с назначенным им цветом, и все встанет на свои места.
Опять неправильно. Я перепробовал почти все, что мог придумать, но даже после того, как нашел строки и столбцов, которые в сумме дают магическое число, я просто не мог получить эти надоедливые диагонали.
Два часа возни с числами, и разочарование взяло верх надо мной. Забудь , подумал я, Я все это выбрасываю. Я снова настроил сетку 4 на 4, игнорируя все правила, которые я установил для себя раньше. 1… 2… 3… 4… Я добавил к первой строке, заполнив всю таблицу в последовательном порядке, пытаясь найти какую-нибудь скрытую подсказку в более упорядоченной сетке.
К моему удивлению, диагонали сложились идеально. Хорошо, оставим диагонали .
Мне потребовалось около 20 секунд, чтобы закончить головоломку оттуда. Все, что мне нужно было сделать, это переместить большие числа вниз, чтобы сбалансировать меньшие, и перетасовать несколько боковых чисел, и… вуаля! Вот так я и решил.
Вы заметите несколько любопытных особенностей этой установки. Во-первых, я поменял местами самые низкие и самые высокие числа (в двух верхних и нижних средних квадратах, а не по диагоналям) и поменял их порядок. Затем я сделал то же самое для левого и правого. Неужели решение магического квадрата может быть таким простым?
Решение дважды четного квадрата
Оказывается, нет. Но эта небольшая подсказка помогла мне открыть технику для любой сетки n- на n , где n делится на 4, или для любого «дважды четного» значения n . По сути, если вы будете следовать тому же шаблону для сетки 8 на 8, вы сохраните поле 4 на 4 в середине и поля 2 на 2 в каждом из углов одинаковыми, а остальные числа поменяйте местами.
соответственно.
Если вы посмотрите на эту сетку, то увидите, что перестановка чисел становится более сложной по мере увеличения квадрата, но все еще может быть решена упорядоченным образом.
Решение квадрата с нечетным номером
Когда дело дошло до сетки с нечетным номером, после некоторого времени попыток найти шаблон, я сдался и сделал быстрый поиск в Google. Оказывается, существует довольно специфический (и простой) способ нахождения магического квадрата с нечетным номером. Начните с 1 в верхнем среднем поле, затем поместите следующее число на одно поле вверх и на одно поле вправо. Но вы выходите из сети , вы думаете, как это работает? Работает, если следовать этим трем простым правилам:
- Если место числа находится за пределами верхней части сетки, вместо этого переместите число в нижнее поле столбца, в котором оно находится (т. е. на один столбец справа от предыдущего числа).
- Если его место выходит за правый край сетки, оставьте число в той же строке, но переместите его в крайний левый столбец сетки.
- Если его место уже занято существующим номером (или он выходит за правый верхний угол), поместите новый номер непосредственно под последним номером, который вы разместили.
Процесс выглядит примерно так:
Решение однократно-четного квадрата
Для сетки 6 на 6 или любой сетки n- х n , где 0 1 n 90 однократно четное» (делится на два, но не на 4), я немного поиграл и обнаружил следующее: если вы просто соберете четыре нечетных квадрата в каждом из углов, как описано выше (для 6 на 6, четыре квадрата 3 на 3), уравновешивая числовые группы, как показано ниже, вы уже более чем на полпути.
Вы заметите, что единственные части, которые не складываются, — это нижняя и верхняя три строки, а также диагонали. После тщательного изучения стало очевидно, что можно просто поменять местами несколько чисел, чтобы добиться идеального баланса.
Более четкая картина появляется, когда вы начинаете входить в большие квадраты, но все равно происходит то же основное переключение между верхними и нижними квадрантами.