Урок 20. Действия с единицами длины
н.1
Условие:
Вырази 3 м 6 дм в дециметрах. Вырази 36 дм в метрах и дециметрах. Преобразование каких счетных единиц тебе это напоминает? Сделай вывод.
Решение:
3 м 6 дм = 30 дм + 6 дм = 36 дм
36 дм = 30 дм + 6 дм = 3 м 6 дм
Советы:
Это напоминает преобразование десятков и единиц.
н.2
Условие:
Вырази в указанных единицах измерения:
1 м 2 дм = … дм
25 дм = … м … дм
5 м 9 дм = … дм
7 м 2 дм = … дм
48 дм = … м … дм
83 дм = … м … дм
Решение:
1 м 2 дм = 10 дм + 2 дм = 12 дм
25 дм = 20 дм 5 дм = 2 м 5 дм
5 м 9 дм = 50 дм + 9 дм = 59 дм
7 м 2 дм = 70 дм + 2 дм = 72 дм
48 дм = 40 дм + 8 дм = 4 м 8 дм
83 дм = 80 дм + 3 дм = 8 м 3 дм
Советы:
Внимательно читайте условие задания.
н.3
Условие:
Сравни, записав в тетради:
5 м ☐ 4 м 9 дм
9 м ☐ 81 дм
6 м 7 дм ☐ 62 дм
84 дм ☐ 8 м 4 дм
3 м 6 дм ☐ 4 м 6 дм
95 дм ☐ 5 м 9 дм
Решение:
5 м > 4 м 9 дм
50 дм > 40 дм + 9 дм
50 дм > 49 дм
9 м > 81 дм
90 дм > 81 дм
6 м 7 дм > 62 дм
60 дм + 7 дм > 62 дм
67 дм > 62 дм
84 дм = 8 м 4 дм
84 дм = 80 дм + 4 дм
84 дм = 84 дм
3 м 6 дм < 4 м 6 дм
30 дм + 6 дм < 40 дм + 6 дм
36 дм < 46 дм
95 дм > 5 м 9 дм
95 дм > 50 дм + 9 дм
95 дм > 59 дм
Советы:
Внимательно читайте условие задания.
н.4
Условие:
Выполни действия:
3 м 6 дм + 4 м 2 дм
8 м 9 дм − 3 м 5 дм
9 м 7 дм − 2 м 1 дм
1 м 4 дм + 5 м 4 дм
2 м 1 дм + 6 м
7 м 5 дм − 3 дм
4 м 3 дм + 5 дм
3 м 8 дм − 3 м
Решение:
3 м 6 дм + 4 м 2 дм = (3 + 4) м + (6 + 2) дм = 7 м 8 дм
8 м 9 дм − 3 м 5 дм = (8 − 3) м + (9 − 3) дм = 5 м 6 дм
9 м 7 дм − 2 м 1 дм = (9 − 2) м + (7 − 1) дм = 7 м 6 дм
1 м 4 дм + 5 м 4 дм = (1 + 5) м + (4 + 5) дм = 6 м 9 дм
2 м 1 дм + 6 м = (2 + 6) м + 1 дм = 8 м 1 дм
7 м 5 дм − 3 дм = 7 м + (5 − 3) дм = 7 м 2 дм
4 м 3 дм + 5 дм = 4 м + (3 + 5) дм = 4 м 8 дм
3 м 8 дм − 3 м = (3 − 3) м + 8 дм = 8 дм
Советы:
Повторите темы Действия с единицами длины
н.5
Условие:
Реши уравнения:
x − 42 = 38
16 + x = 51
900 − x = 200
Решение:
x − 42 = 38
x = 38 + 42
x = 80
16 + x = 51
x = 51 − 16
x = 35
900 − x = 200
x = 900 − 200
x = 700
Советы:
Увеличить число на несколько единиц — использовать действие сложение, знак»+» Уменьшить на несколько единиц- использовать действие вычитание, знак «-«.
н.6
Условие:
а) Саша измерил длину и ширину своей комнаты. Оказалось, что длина комнаты равна 3 м 4 дм 6 см, а ширина − 2 м 3 дм 1 см. На сколько длина комнаты больше ширины?
б) От куска ленты отрезали 4 м 6 дм 2 см, а потом еще 5 м 1 дм 3 см. Сколько всего отрезали ленты?
Решение:
Решение а
3 м 4 дм 6 см − 2 м 3 дм 1 см = (3 − 2) м + (4 − 3) дм + (6 − 1) см = на 1 м 1 дм 5 см − длина комнаты больше ширины.
Ответ: на 1 м 1 дм 5 см.
Решение б
4 м 6 дм 2 см + 5 м 1 дм 3 см = (4 + 5) м + (6 + 1) дм + (2 + 3) см = 9 м 7 дм 5 см − ленты отрезали всего.
Ответ: 9 м 7 дм 5 см
Советы:
Сложение — это математическое действие. Числа, которые складываются, называются слагаемыми. Вычитание — обратное сложению арифметическое действие, посредством которого от одной величины отнимается другая величина.
н.7
Условие:
Математические загадки
а) Игорь задумал число, прибавил к нему 400 и получил 900. Какое число задумал Игорь?
Какое число задумал Игорь?
б) Таня тоже задумала число, вычла из него 600 и получила 200. Какое число задумала Таня?
в) Борис вычел задуманное им число из 700 и получил ответ 300. Какое число задумал Борис?
Решение:
Решение а
900 − 400 = 500 − задумал Игорь.
Ответ: 500
Решение б
200 + 600 = 800 − задумала Таня.
Ответ: 800
Решение в
700 − 300 = 400 − задумал Борис.
Ответ: Борис.
Советы:
Задача на нахождение остатка решается действием вычитания. знак «+»
н.8
Условие:
Белка принесла в дупло в первый день 7 орехов и 6 грибов. Во второй день − 9 орехов, а грибов − на 5 больше, чем орехов.
Поставь вопросы к этому условию и ответь на них.
Решение:
Сколько грибов принесла белка во второй день?
9 + 5 = 14 (грибов)
Сколько всего орехов принесла белка за 2 дня?
7 + 9 = 16 (орехов)
Сколько всего грибов принесла белка за 2 дня?
6 + 14 = 20 (грибов)
На сколько меньше орехов принесла белка за два дня, чем грибов?
20 − 16 = на 4 (ореха).
На сколько больше орехов принесла больше белка во второй день, чем в первый?
9 − 7 = на 2 (ореха)
На сколько больше грибов принесла больше белка во второй день, чем в первый?
14 − 6 = на 8 (грибов)
Советы:
Задача на нахождение остатка решается действием вычитания. знак «+»
н.9
Условие:
Ежу надо пройти до домика 80 м. Он прошел сначала 26 м, потом на 9 м больше и решил передохнуть. Сколько метров ему осталось пройти до домика?
Решение:
1) 26 + 9 = 35 (м) − прошел еж потом;
2) 26 + 35 = 61 (м) − прошел еж всего;
3) 80 − 61 = 19 (м) − осталось ежу пройти до домика.
Советы:
Ответ: 19 м
н.10
Условие:
Запиши число 6:
а) тремя одинаковыми цифрами;
б) двумя одинаковыми цифрами;
в) шестью одинаковыми цифрами.
Решение:
Решение а
2 + 2 + 2 = 6
Решение б
3 + 3 = 6
Решение в
1 + 1 + 1 + 1 + 1 + 1 = 6
Советы:
Внимательно читайте условие задания.
н.11
Условие:
Найди три последовательных числа, сумма которых равна:
а) 15;
б) 21;
в) 30.
Решение:
Решение а
4 + 5 + 6 = 9 + 6 = 15
Ответ: 4, 5, 6.
Решение б
6 + 7 + 8 = 13 + 8 = 21
Ответ: 6, 7, 8.
Решение в
9 + 10 + 11 = 19 + 11 = 30
Ответ: 9, 10, 11.
Советы:
Увеличить число на несколько единиц — использовать действие сложение, знак»+» Уменьшить на несколько единиц- использовать действие вычитание, знак «-«.
«Единицы длины. Километр» (2 класс)
Тема урока: «Единицы длины. Километр»
Тип урока: Урок открытия новых знаний.
Цель урока: создать условия для знакомства с новой единицей длины – километр. Дать представление об использовании данной величины на практике, о соотношении с другими известными мерами длины.
Задачи:
Образовательная:
1.Подвести учащихся к «открытию» новой единицы длины – километр, его соотношение с единицей длины – метром.
2.Формировать умение выражать длину в заданных единицах (м, км).
3.Решать текстовые задачи, содержащие единицы длины.
4.Совершенствовать умения и навыки по чтению и записи многозначных чисел; отработка вычислительных навыков, умения пользоваться линейкой.
Развивающая:
Способствовать развитию умения правильно применять математические величины.
Способствовать развитию мыслительных операций: анализа, синтеза, обобщения, сравнения; развивать логическое мышление, речь, память, внимание.
Развивать умение грамотно, логично, полно давать ответы на вопросы, уметь доказывать, аргументировать своё мнение.
Формировать навыки самостоятельной индивидуальной и коллективной работы: взаимоконтроля и самопроверки, обсуждения информации, планирования познавательной деятельности и самооценки, развитие умения работать в паре.
Воспитательная:
1.Воспитывать интерес к математике; создать мотивацию к дальнейшему изучению предмета; стремление использовать математические знания в повседневной жизни.
2.Содействовать развитию у детей умения общаться, радоваться успехам товарищей.
3.Помочь учащимся осознать ценность совместной деятельности.
4.Воспитывать информационную культуру, дисциплинированность, аккуратность, настойчивость в учебе, ответственность за выполняемую работуОборудование: учебник Л. Г. Петерсон, 2 класс, 3 часть (программа «Перспектива»), презентация.
Ход урока:
-Здравствуйте, ребята! Меня зовут Виктория Алексеевна и сегодня я проведу у вас урок математики.
-Приветствие учителя.
1. Мотивация (Самоопределение к учебной деятельности)
-Ребята, вы когда-нибудь наблюдали за ночным небом? (Да)
— Что вы видели? (Звёзды и Луну.)
-Сегодня я предлагаю вам совершить космический полёт на Луну. Вы должны быть достойными представителями Земли, поэтому должны взять с собой все свои знания и умения. А поможет нам в этом наука – математика.
А поможет нам в этом наука – математика.
— Позвольте мне быть руководителем полёта, а вы будете – экипажем космической ракеты.
— Экипаж к полёту готов? (Да)
Проверьте осанку в кабине ракеты. Всё ли на месте?(Да)
Проверьте положение бортового журнала.
Записи нужно делать чётко, разборчиво, чтобы их смогли читать все космонавты Земли, которые будут следить за нашим полётом.
— Зафиксируйте в бортовом журнале дату отправления. (Дети записывают число, классная работа)
2. Актуализация знаний и фиксирование индивидуального затруднения в пробном учебном действии.
— Ребята, что делают космонавты, когда отправляются в полёт? ( Они всегда что – то изучают, наблюдают, делают какие – то новые открытия.)
— Вот и мы сегодня будем не просто путешествовать по космосу, но и узнаем что – то новое.
(Задание показано на слайде, работа выполняется у доски и в тетради)
В 550-20= (530)
Ы 100:5= (20)
Н 3⋅ 40= (120)
И 140+160= (300)
Л 280+90= (370)
Е 400+95= (495)
Ч 30⋅7 = (210)
И 240 – 60= (180)
(Самопроверка по эталону)
– Расположите ответы в порядке убывания.
—Правильно, ребята, у нас получилось слово «величины».
Тема раздела, по которому мы будем работать сегодня на уроке называется
3. Выявление места и причины затруднения
-Давайте вспомним, что такое величина? (Величина – это то, что можно измерить)
-Ребята, а какие величины вы знаете? (Длина, масса, время, площадь, объём)
-В каких единицах измеряют время? (секунда, минута, час, сутки, год)
-В каких единицах измеряют массу? (грамм, килограмм)
-В каких единицах измеряют длину? (мм, см, дм, м)
-А какую единицу длины из перечисленных вы выберите для измерения длины нашего города? (Никакую, все единицы измерения очень маленькие)
-Что же нам делать? Как быть? (Наверно есть единица длины больше метра)
4. Построение проекта выхода из затруднения
Построение проекта выхода из затруднения
-Так какова же цель нашего урока? (Цель вывешивается на доску)
(Узнать, новую единицу длины и для чего она нужна. Узнать о соотношении этой единицы длины с уже известными единицами длины )
5. Реализация построенного проекта
-Как вы думаете, есть единица длины больше метра? (Да)
-Предположите, как она называется? (Километр)
-Исходя из моих вопросов, кто постарается сформулировать тему нашего урока? (Единица длины — километр)
-А для чего нам нужна такая единица длины, как километр? (Для измерения больших расстояний)
— Из каких двух частей образовалось это слово? (кило + метр)
-Часть слова метр нам уже знакома, а может быть кто-то знает, что означает слово кило? (Нет)
-Слово «кило» взято из французского языка и означает тысяча.
-Кто расшифрует секрет этой единицы? (Тысяча метров)
-Как вы думаете, как будем писать слово километр сокращено? (километр — км)
-Верно! Давайте запишем в тетрадь вывод:
1 км=1000 м.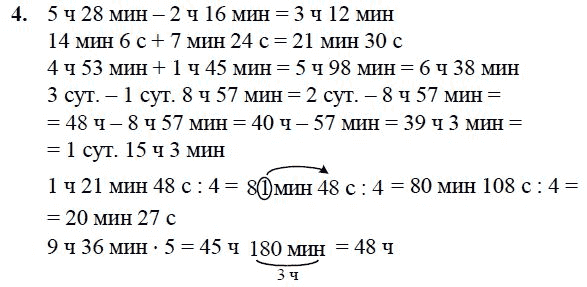
6. Первичное закрепление и проговаривание во внешней речи
-Ребята, откройте учебники на стр.88.
—Давайте внимательно рассмотрим рамку, которую нам предоставляет автор и ознакомимся с соотношениями между единицами длины.
— А теперь выполним задание 1.
(Работа выполняется у доски и в тетради)
Решение:
2см 3 мм=23 мм
1дм 7 см 3 мм=173 мм
5 дм 2 мм=502 мм
6 м 3 дм 7 см = 637 см
9 м 8 дм=980 см
4 м 1 см=401 см
Задание 2, стр. 88.
(Работа выполняется у доски и в тетради)
Решение:Задание 3, стр. 88.
(Работа выполняется у доски и в тетради)
Решение:
-Ребята, давайте начертим схему и заполним ее.
-Что нам известно? (Нам известно, что в первый день туристы прошли 12 км, а во второй — на 4 км больше, чем в первый, а в третий день – в 4 раза меньше, чем в первый и во второй дни вместе)
-Что нам необходимо найти?( Нам необходимо найти, сколько км прошли туристы за три дня)
Найдем, сколько км туристы прошли в первые два дня:
12+(12+4)=12+16=28(км)
Найдем, сколько км прошли туристы за третий день:
28:4=7(км)
Найдем, сколько всего км прошли туристы за три дня:
28+7=35(км)
Ответ: 35 км прошли туристы за три дня.
— А теперь давайте потихоньку встанем и немного разомнемся!
(Учитель показывает движения, дети повторяют за ним)
Физминутка:
Не зевай по сторонам,
Ты сегодня – космонавт. (Повороты в стороны)
(Повороты в стороны)
Начинаем тренировку, (Наклоны вперед)
Чтобы сильным стать и ловким.
Ждет нас быстрая ракета (Приседают)
Для полета на планету.
Отправляемся на Марс. (Кружатся)
Звезды в гости ждите нас.
Крыльев нет у этой птицы,
Но нельзя не подивиться:
Лишь распустит птица хвост – (руки назад, в стороны)
И поднимется до звезд. (тянемся вверх)
-Молодцы, ребята, вы отлично справились!
7. Самостоятельная работа с самопроверкой по эталону
-Продолжим нашу работу, откройте стр.88, задание 4.
(Решаем задачу самостоятельно, кто решит быстрее, поднимите руку.
Решение:
-Что нам известно? (Нам известно, что всего лыжник должен пройти 132 км, а так же, что в течении 3-х дней он проходит по 35 км в один день)
—Что нам необходимо найти? ( Нам нужно найти, сколько км ему осталось пройти)
-Для начала, нам необходимо найти, сколько км прошел лыжник за три дня:
1)3⋅35=3⋅(30+5)=3⋅30+3⋅5=90+15=105(км)
-А теперь найдем, сколько км ему осталось пройти:
2)132-105=27(км)
Ответ: 27 км осталось пройти лыжнику.
-Посмотрите на экран. Итак, проверяем.
-Все получили правильный ответ? Если, у кого-то возникли трудности, запишите правильное решение и еще раз посмотрите на него.
-Оцените свою работу и запишите результат в лист самооценивания.
8.Включение новых знаний в систему знаний и повторений
-Теперь выполним задание номер 7, на повторение, стр.89
(Работа выполняется у доски и в тетради)
Решение:
9.Итог урока
-Итак, ребята, с какой новой единицей длины мы сегодня познакомились на уроке? (Километр)
-Для чего нам нужна такая единица длины, как километр? (Для измерения больших расстояний)
— Из каких двух частей образовалось это слово? (кило + метр)
— Сколько метров в 1 километре? (1000)
—Все ли задания были легкими и доступными? (Да)
10. Рефлексия учебной деятельности
Рефлексия учебной деятельности
—Ребята, вы все сегодня хорошо постарались, молодцы! Спасибо за активность, урок окончен!
Математика 2 класс | |||
Дата: 22.04.2014 г. | |||
Тема: Единицы длины . Миллиметр. | |||
Цели: Познакомить с новой единицей длины – миллиметром. Вывести соотношение сантиметра и миллиметра. Сформировать умение измерять длину отрезков в миллиметрах, складывать и вычитать длины отрезков. Переводить более крупные единицы измерения длины в более мелкие и наоборот. Тренировать вычислительный навык, решать текстовые задачи. Использовать полученные знания в учении и повседневной жизни. Прививать любовь к урокам математике. | |||
Оборудование: Интерактивная доска, классная доска, таблицы мер длины, индивидуальные карточки, лестница успеха для рефлексии. | |||
Тип урока: Урок открытия нового знания | |||
Учебник: Математика «Учись учиться». 2 класс часть 3 Л. Г. Петерсон УМК «Перспектива» | |||
Этапы урока | Деятельность учителя | Деятельность учащихся | Форма организации учебно- познавательной деятельности |
1. Мотивация (самоопределение) к деятельности | Психологический настрой. Посмотрите на своего товарища, протяните ему свои ладошки и постарайтесь передать тепло своей ладошки. Улыбка, сопереживание, готовность помочь – это так необходимо в нашей жизни. Внимание! Проверь, дружок, —Сегодняшний урок начнём с задания, которое вам поможет определить, чему будет посвящён урок. Кроме того, это задание полезно тем, что тренирует вашу память. Учитель читает пары чисел 2-3 раза: 102;18 26;1 98;555 9;57 40;800 69;90 3;77 6;81 Назовите эти числа. -А теперь посмотрите на доску. Найдите среди чисел на доске, те числа, которые вы запомнили. — Проверим, правильно ли вы назвали числа.
| Карточки с числами (на доске) 102,555,800,903,1,9,6,3, 18-В 26-Е 98-Л 57- И 40 – Ч 69- И 77 – Н 81 — А | фронтально Фронтальная, коллективная |
2. Актуализация знаний: повторение изученного материала | 1.Открыть тетради, записать число, классная работа. 2.Я предлагаю начать с решения задач. -Какие ответы вы получили? (30 дм³, 28 см².)
При каких условиях возможны действия с величинами? (Если они выражены в одинаковых единицах измерения.) | — Прочитайте задачи. — Запишите решение задачи ,без краткой записи. Задачи на интерактивной доске. 1.Весной Федя сделал скворечник. Его длина – 3 дм, ширина – 2 дм, высота – 5 дм. Чему равен объём скворечника? 2.Ширина прямоугольника 4 см, длина – на 3 см больше. Вычислите площадь этого прямоугольника. Оценить свою работу на лестнице успеха. Оценка на лестнице успеха | Индивидуальная Фронтальная устная |
3. Постановка учебной задачи | -Какой единицей вы воспользуетесь, измеряя длину: карандаш– см дом- м парта –дм дерево – м тетрадь — см Муравей — ? — Почему вы не можете ответить на последний вопрос? ( Самая маленькая из известных нам единиц измерения длины- сантиметр, но для измерения длины муравья нужна единица еще меньше. — Какую цель мы поставим перед собой на уроке? ( Узнать о новой единице измерения длины, которая меньше, чем сантиметр, научить чертить отрезки, сравнивать с новой единицей измерения, выполнять вычисления используя новую единицу измерения ). | Наглядное пособие: на интерактивной доске карандаш– см дом- м парта –дм дерево – м тетрадь — см Муравей — ? | Фронтальная ,устная |
4. Открытие нового знания |
-Измерьте и запишите длину отрезка в сантиметрах.
Учитель открывает на доске таблицу мер длины . Найдите карточку № 2 -Что нужно сделать в данном задании? (Измерить длину отрезка.)
Учащиеся выполняют пробное действие на карточках . Учащиеся поднимают руки.
Учащиеся поднимают руки. Несколько ответов учитель может выписать на доску. Вероятно, что среди ответов будут 3 см 2 мм, 3 см 4 мм. Затруднение фиксируется так:
Учащиеся в замешательстве, так как нет соответствующего правила, нужной единицы измерения на эталоне
Один из учащихся читает правило вслух.
Один из учащихся мелом дописывает открытую на 2 этапе урока таблицу соотношения мер длины .
Учитель дописывает тему урока. Музыкальная физминутка «Танец маленьких утят»
Учащиеся самостоятельно измеряют длину отрезка ОМ.
( Измерение отрезков на доске) — Поднимите руку , кто научился чертить отрезки с новой единицей измерения? — А кто еще не умеет чертить отрезки с новой единицей измерения? — Молодцы! Мы с вами уже научились чертить отрезки с новой единице длины — А что еще мы можем делать с величинами? ( Сравнивать) — Эта схема поможет вам узнавать не только соотношение между «соседними» единицами длины, но и, например, сколько в одном дециметре миллиметров.
| Карточка № 1 1м 1дм 1см 10 10 10 Таблица мер длины: 1м=10 дм 1дм=10 см Карточки для пробного действия Карточка № 2 О М ОМ = _________ Дописать эталон 1м 1дм 1см 1мм 10 10 10 Запись темы урока на доске Миллиметр На доске изображение линейки. 4см 6 мм, 7см 3мм 1м 1дм 1см 1мм 10 10 10 1дм =100 мм 1м = 1000 мм | Индивидуальная Индивидуальная Фронтальная Запись ответов на доску: 3см 2 мм, 3см 4см Индивидуальная, коллективная |
5. Первичное закрепление с проговариванием | № 4, стр. 80 (1-2 столбики)
( Будем работать на следующем уроке) Итог: Мы с вами уже научились сравнивать величины. -При каких условиях можно сравнивать величины? (Если они выражены в одинаковых единицах измерения) | Проверка по слайду 1м>1 мм 1000 мм>1мм 1см=10 мм 10мм=10 мм 100 мм=1дм 100 мм=100 мм 10 дм>1см 100 см >1 см 1000 мм =100 см 1000 мм = 1000 мм 10 см >10 мм 100мм > 10 мм | Работа в парах. Проговариваем во внешней речи. — Я буду ходить между рядами и слушать ,как вы проговариваете. (1м = 1000 мм, следовательно 1 м > 1 мм и т. д.) Дополнительно : ( Дописать мелом на доске) -Кто все сделал, выполнит задание на доске. 2м …1мм 1дм …1мм |
6. Самостоятельная работа с самопроверкой по эталону. |
миллиметров, в 1 сантиметре 10 миллиметров, а в двух – 20, да еще 5 миллиметров. Значит всего 125 миллиметров. Записываю ответ 125 мм. Проверим работу по эталону. -Кто справился без ошибок? -Кто понял , как выражать единицы длины в миллиметрах? А кто еще не понял?(Значить на следующем уроке мы продолжим работу ) — А № 5 ( в, г) выполните дома. Итак: Мы научились выражать единицы длины в миллиметрах. Молодцы -Что еще мы умеем делать с величинами? (Складывать и вычитать ) | Вырази в миллиметрах ( На доске) а) 1дм 2 см 5 мм = мм б) 4 дм 8 мм = мм в) 23 см 8 мм = мм г) 3 дм 5 см = мм 2 дм 3 см 4мм = мм 3 дм 7 мм = мм 45 см 6мм = мм 8 дм 4 см = мм | Для сильных самостоятельная работа Со слабыми работаю индивидуально |
7. Включение нового задания в систему заданий и повторение. | Давайте попробуем выполнить задание № 6 на с. 80 — Проверьте.
| Учащиеся выполняют самостоятельную работу в рабочих тетрадях. (Сильные выполняют работу сами). Кто затрудняется — с комментированием на доске. | Проверка работы – коллективная . |
8. Рефлексия деятельности на уроке. | -С какой единицей измерения длины мы сегодня познакомились? -Что удобно измерять в миллиметрах? Давайте вернемся к началу урока. -Так какой же единицей измерения мы воспользуемся для измерения муравья?(мм) — А что еще мы можем измерить в миллиметрах? (Ластик, толщину тетради, учебника). -Сколько миллиметров в 1 см, в 1 дм, в 1 м?
Давайте сделаем в тетрадь маленькую самостоятельную работу и убедимся достигли ли мы поставленной цели или нет. Пожалуйста, приготовьте ваши лестницы успеха. — Если у вас 6 или 7 точек на верхней ступени, то вы освоили материал на высоком уровне. — Если у вас от 5 до 3 точек то вы освоили материал на среднем уровне. -Если у вас меньше 3 точек , то надо работать еще. | Оценивание работы на уроке. Лестница успеха | Наглядность- Муравей Самостоятельная работа Карточка № 3 1.Начертить отрезок длиной 37 мм 2.Вырази в миллиметрах: 1дм 4см 2 мм = мм 3.Вычисли: 6дм 5см 3мм+ 2дм 1мм= ( 854 мм= 8 дм 5см 4мм) Проверка работы : фронтальная. |
9. Домашнее задание. | № 3, стр. 79,№ 7 (а) стр.80,а остальные задания по желанию на с. 80-81,Попробуйте измерить дома маленькие предметы в миллиметрах. | ||
3 класс, часть 1 – 2 Консультация 3. Уроки 1 – 13.
3 класс, часть 1 – 2Консультация 3. Уроки 1 – 13.На уроках 1 – 5 систематизируются знания учащихся о единицах измерения длины и массы, вводятся новые единицы измерения массы: грамм, центнер, тонна, закрепляются соотношения между единицами измерения длины, массы, умение выражать значения величин в разных единицах измерения. Также повторяются и закрепляются нумерация и действия с многозначными числами, решение текстовых задач, уравнений, примеров на порядок действий, умножение чисел в столбик, измерение отрезков и построение отрезков данной длины, понятие объема прямоугольного параллелепипеда, отрабатываются вычислительные навыки.
На уроке 1 воспроизводится таблица, устанавливающая соотношение между единицами длины, с которой учащиеся уже встречались раньше:
Теперь область применения этой таблицы существенно расширяется. В №1, стр. 95 проговариваются все возможные соотношения между этими единицами. Например, устанавливается, что 1 км = 1000 м = 10 000 дм = 100 000 см = 1 000 000 мм и т. д. При этом надо вспомнить правило: при переходе к меньшим меркам выполняется умножение, а при переходе к большим меркам – деление. Соответствующие коэффициенты перехода (числа, на которые надо умножать или делить при переходе от одной единицы измерения к другой) записаны под дугами.
В № 2–4, стр. 95 учащиеся используют установленные соотношения и аналогию с десятичной системой записи чисел для перевода длин из одних единиц измерения в другие. Решение примеров записывается в тетради в клетку и проговаривается вслух. Способ обоснования может быть различным – на основе установленного правила либо на основе аналогии с десятичной системой записи чисел, например:
а) 7 м = 700 см, так как в 1 метре 100 сантиметров, а 100 · 7 = 700,
или
7 м = 700 см, так как 7 метров – это 7 сотен сантиметров;
б) 16 000 мм = 1600 см, так как в 1 сантиметре 10 миллиметров, а
16 000 : 10 = 1600,
или
16 000 мм = 1600 см, так как в 16 000 содержится 1600 десятков;
в) 12 км 50 м = 12 050 м, так как в 1 километре 1000 метров, значит,
в 12 км – 12 000 м, да еще 50 м, всего получится 12 050 метров,
или
12 км 50 м = 12 050 м, так как 12 км 50 м – это 12 тысяч 50 метров.
Основным способом является первый, так как он универсальный и используется, например, и при преобразовании единиц времени, где соотношения между единицами не являются десятичными. Однако акцент на аналогию системы мер длины и массы с десятичной системой записи чисел не только поможет закрепить знание нумерации, но и покажет связь изучения чисел с практическими задачами. Каждый из учеников может выбрать тот способ обоснования, который ему удобен, а в классе должны звучать оба способа.
Перед выполнением заданий № 5–6, стр. 96 надо повторить с учащимися правило о том, что величины можно сравнивать, складывать и вычитать только тогда, когда они выражены в одних и тех же единицах измерения. Поэтому для сравнения, сложения и вычитания величин в этих заданиях надо их сначала выразить в одинаковых мерках.
На уроке 2 в №1–2, стр. 98 учащиеся решают практические задачи, связанные с построением отрезков и измерением их длин. В №1 они устанавливают, что если точки A, B и C лежат на одной прямой, то длина AC равна сумме длин AB и BC, а если нет, то длина AC меньше суммы длин AB и BС. Другими словами, прямая линия, соединяющая две точки A и C, короче ломаной ABC. В №2 они строят планы земельных участков треугольной и четырехугольной формы и вычисляют их периметры. Таким образом, их внимание еще раз обращается на то, что числа возникли для решения практических задач, поэтому естественно, что соотношения между единицами измерения величин аналогичны принципу нумерации. Эта аналогия еще раз подчеркивается в №3, стр. 98. В заданиях №4–5, стр. 98 рассматриваются более сложные случаи перевода единиц длины.
Другими словами, прямая линия, соединяющая две точки A и C, короче ломаной ABC. В №2 они строят планы земельных участков треугольной и четырехугольной формы и вычисляют их периметры. Таким образом, их внимание еще раз обращается на то, что числа возникли для решения практических задач, поэтому естественно, что соотношения между единицами измерения величин аналогичны принципу нумерации. Эта аналогия еще раз подчеркивается в №3, стр. 98. В заданиях №4–5, стр. 98 рассматриваются более сложные случаи перевода единиц длины.
На уроках 3–4 аналогичным образом рассматриваются единицы массы и соотношения между ними:
Правило перевода единиц и способы перевода остаются прежними, изменяются лишь названия единиц и переводные коэффициенты. Кроме того, рассматриваются виды гирь, которые обычно используются при взвешивании, и способы уравновешивания предметов на чашечных весах.
Хотим отметить, что при выполнении №10, стр. 99 следует обратить внимание на некоторые моменты. К настоящему времени дети уже знают, что одни и те же математические выражения могут описывать разнообразные жизненные ситуации. Так, выражение 2 + 3 может быть суммой игрушек, ручек, тракторов и еще чего угодно, в том числе «шклидулок». И от того, что мы не знаем, что такое «шклидулка», суть вычислений не изменится – мы все равно получим в ответе 5.
99 следует обратить внимание на некоторые моменты. К настоящему времени дети уже знают, что одни и те же математические выражения могут описывать разнообразные жизненные ситуации. Так, выражение 2 + 3 может быть суммой игрушек, ручек, тракторов и еще чего угодно, в том числе «шклидулок». И от того, что мы не знаем, что такое «шклидулка», суть вычислений не изменится – мы все равно получим в ответе 5.
В задаче предлагается вымышленная ситуация – о шклидулках и бримазятах. Математическая структура задачи не представляет для учеников труда, но здесь они должны суметь перенести ее на абстрактное для них содержание и провести рассуждения во всей полноте.
– Чтобы ответить на первый вопрос задачи, можно сложить шклидулки, которые нашли бримазище и бримазенок. (Ищем целое.) Для этого сначала из 96 вычтем 64 и узнаем, сколько шклидулок нашел бримазенок. Чтобы узнать, во сколько раз больше шклидулок нашел бримазище, чем бримазенок, надо первое число разделить на второе.
1) 96 – 64 = 32 (ш.) – нашел бримазенок.
2) 96 + 32 = 128 (ш.).
3) 96 : 32 = 3 (раза).
Ответ: вместе они нашли 128 шклидулок, бримазище – в 3 раза больше бримазенка.
При выполнении №12, стр. 103 следует рассуждать так:
Р – 70 Г – 200 С – 40
И – 80 К – 5400 Б – 400
П – 50 О – 4800 Н – 100
СПРИНГБОК. Один из интереснейших видов газелей, обитающий в Южной Африке. Верхняя сторона тела – желто‑коричневая, нижняя сторона – белая, на границе проходит контрастная буровато‑черная полоса. Но самая замечательная особенность спрингбока – обширная продольная кожная складка на спине. Когда животное спокойно, складку не видно. Но, почувствовав опасность, спрингбок начинает подпрыгивать на месте, отталкиваясь одновременно всеми ногами, без видимых усилий, как резиновый мяч.
Прыжки спрингбока колоссальны: до 2 м в высоту. При этом края кожной складки расходятся, и выстилающий ее белый мех начинает ослепительно сверкать. Для всех обитателей саванны прыжки спрингбока служат сигналом опасности.
Для всех обитателей саванны прыжки спрингбока служат сигналом опасности.
Спрингбок знаменит своими странствиями. К сожалению, говорить о них приходится лишь в прошедшем времени: они прекратились вместе с резким уменьшением численности спрингбока. Во время последнего крупного переселения спрингбоков в 1896 году животные плотной массой покрывали участок шириной около 25 км, а длина колонны составляла 220 км!
Во второй части учебника закрепляются нумерация, сложение и вычитание многозначных чисел, вводится умножение и деление многозначного числа на однозначное, рассматриваются некоторые преобразования на плоскости (параллельный перенос, симметрия), меры времени и календарь, на основе некоторых логических понятий (высказывание, истинное и ложное высказывание) уточняется понятие уравнения и рассматриваются новые их виды. Учащиеся знакомятся с понятиями переменной и выражения с переменной, учатся находить значения выражений с переменной, строить формулы зависимостей между величинами.
На уроках 6 – 9 у учащихся формируется умение умножать многозначные числа на однозначные и умножать круглые числа в случаях, сводящихся к умножению на однозначное число, учатся решать задачи на нахождение значений величин по их сумме и разности. Ученики повторяют и закрепляют нумерацию, сложение и вычитание многозначных чисел, решение текстовых задач, решение уравнений с комментированием по компонентам действий, сравнение выражений, действия с единицами длины и массы.
Простейшие случаи умножения многозначного числа на однозначное (27 · 5, 140 · 3 и т. д.) и их запись в столбик уже встречались учащимся. На данном этапе обучения они должны распространить известный им способ умножения в столбик на общий случай умножения многозначного числа на однозначное, и отработать его для сложных случаев. Работа ведется, как обычно, деятельностным методом.
На уроке 6 на этапе актуализации знаний с учащимися нужно вспомнить распределительное свойство умножения. Для этого можно рассмотреть с ними различные способы нахождения площади прямоугольников для случаев, когда прямоугольник разбит на 2 части и на 3 части:
По данным рисункам ставятся вопросы:
1) Чем похожи и чем отличаются эти задачи? (В первой задаче прямоугольник разбит на две части, а во второй – на три. )
)
2) Как называется первое равенство? (Правило умножения суммы на число, или распределительное свойство умножения.)
3) Можно ли распространить это правило на сумму трех слагаемых? (Из второго равенства следует, что да.)
4) Можно ли его распространить на сумму большего числа слагаемых? (Да, ведь прямоугольник можно разбить на большее число частей.)
Чтобы поставить проблему, учащимся можно сначала предложить решить в тетрадях в клетку следующие примеры и выявить в них закономерности:
Ученики могут заметить, что:
1) все примеры – на умножение;
2) первый множитель увеличивается, а второй не изменяется;
3) с увеличением первого множителя произведение увеличивается;
4) если первый множитель увеличивается в 10 раз, то и все произведение
увеличивается в 10 раз.
Затем учитель предлагает, воспользоваться тем же вычислительным приемом и решить пример
При решении примера, вероятно, возникнет затруднение: могут получиться разные ответы, кто‑то из детей не решит его и т. д. Возникшая проблемная ситуация и мотивирует поиск нового способа действий.
д. Возникшая проблемная ситуация и мотивирует поиск нового способа действий.
В случае, если с последним примером справятся все обучающиеся, можно попросить их обосновать решение. Главное – дети должны заметить, что для решения данного примера используется другой вычислительный прием. Этот признак отличия они должны проговорить вслух: в первых четырех примерах требуется умножить двузначное число на однозначное, а в последнем примере – трехзначное на однозначное.
После этого цель урока может быть сформулирована следующим образом: установить, как умножается любое многозначное число на однозначное. Если последний пример выполнят все ученики, то цель урока мотивируется необходимостью обосновать правомерность используемого приема.
Этап «открытия» нового знания начинается с выбора метода рассуждений. Рассмотренная в начале урока задача о вычислении площадей прямоугольников должна помочь учащимся вспомнить, что алгоритм умножения двузначного числа на однозначное был установлен на основе правила умножения суммы на число (распределительного свойства умножения), и сориентироваться на это свойство.
В № 1, стр. 1 еще раз проговаривается формулировка правила умножения суммы на число и возможность его распространения на любое число слагаемых. Затем в № 2 (а), стр. 1 данное число 576 разбивается на удобные слагаемые 500 + 70 + 6 и на основе этого правила выполняются преобразования:
Очевидно, что такая запись является слишком громоздкой, неудобной, – это учащиеся скажут сразу. Тогда ставится задача найти более короткий способ записи по аналогии с умножением на двузначное число. Если самостоятельно ученики затруднятся это сделать, можно предложить им проанализировать слагаемые суммы по рисунку №2 (б), стр. 1. Дети должны заметить, что при вычислении суммы сначала подсчитывается число единиц, затем число десятков и число сотен (нули при сложении результата не изменяют). И поскольку все эти числа всегда являются двузначными (значения табличных произведений), то удобнее число единиц следующего разряда, которое «запоминается», писать вверху над соответствующим разрядом первого множителя, как при умножении двузначных чисел. Подвести учащихся к этому выводу можно следующей последовательностью вопросов:
Подвести учащихся к этому выводу можно следующей последовательностью вопросов:
1) Как получили слагаемые суммы? (6 единиц умножили на 9, потом 7 десятков умножили на 9, а потом 5 сотен умножили на 9.)
2) Всегда ли во втором слагаемом на конце будет нуль? Почему? (Всегда, так как считаем число десятков.)
3) Всегда ли в третьем слагаемом на конце 2 нуля? Почему? (Всегда, так как считаем число сотен.)
4) Почему во втором столбике нули зачеркнуты? (Они не изменяют значение суммы.)
5) Может ли число единиц, десятков или сотен «заходить» не на один следующий разряд, а на 2 или 3 разряда? (Нет, перемножаем однозначные числа, поэтому в произведении не может быть больше двух знаков.)
6) Сравните запись умножения во втором и третьем столбике – какая из записей удобнее? (В третьем столбике.)
7) Догадайтесь, как она получается из предыдущей? (Сначала умножаем единицы: 6 · 9 = 54, 4 единицы пишем, а 5 десятков запоминаем – записываем над числом десятков первого множителя. Потом умножаем десятки: 7 · 9 = 63, 63 + 5 = 68, 8 десятков пишем, а 6 сотен запоминаем. А потом умножаем сотни: 5 · 9 = 45, 45 + 6 = 51, записываем 51 сотню. – «Открытие».)
Потом умножаем десятки: 7 · 9 = 63, 63 + 5 = 68, 8 десятков пишем, а 6 сотен запоминаем. А потом умножаем сотни: 5 · 9 = 45, 45 + 6 = 51, записываем 51 сотню. – «Открытие».)
Пишу: множитель 9 под разрядом единиц множителя 576.
Умножаю единицы: 6 · 9 = 54 ед., пишу 4 в разряде единиц,
а 5 д. запоминаю.
Умножаю десятки: 7 · 9 = 63 д., 63 + 5 = 68 д., пишу 8 в разряде
десятков, а 6 с. запоминаю.
Умножаю сотни: 5 · 9 = 45 с., 45 + 6 = 51 с., пишу 1 в разряде
сотен, а 5 – в разряде тысяч.
Ответ: 5184.
В завершение учитель спрашивает у детей, изменятся ли рассуждения при умножении на однозначное число четырехзначного, пятизначного, шестизначного и т. д. числа. Как правило, дети легко распространяют полученный вывод на любое многозначное число. Тогда в тетради в клетку надо записать, решить и прокомментировать (с возможной помощью учителя) более сложный случай умножения, например, 5 · 20 156. Внимание детей обращается на порядок множителей и на то, что в данном случае также удобно писать однозначный множитель под разрядом единиц многозначного множителя.
Внимание детей обращается на порядок множителей и на то, что в данном случае также удобно писать однозначный множитель под разрядом единиц многозначного множителя.
Если у учащихся все же возникнет сомнение в правомерности распространения полученного вывода на случай умножения любого многозначного числа на однозначное, то можно рассмотреть аналогичным образом умножение четырехзначного числа на однозначное или предложить учащимся сделать это дома самостоятельно.
Примеры для этапа первичного закрепления подбираются в зависимости от уровня подготовленности класса. Можно, например, решить с подробным комментированием в громкой речи № 3 (а), стр. 1, а для этапа самоконтроля использовать № 3 (б), стр. 1. После выполнения самостоятельной работы ученики сопоставляют свое решение с образцом, предъявленным учителем, и убеждаются в том, что новый вычислительный прием ими освоен. Напомним, что при изучении нового материала первостепенное значение имеет создание ситуации успеха для каждого ребенка. Возможные ошибки должны здесь же исправляться, а материалы дорабатываться индивидуально, пока остальные учащиеся класса решают задачи на повторение.
Возможные ошибки должны здесь же исправляться, а материалы дорабатываться индивидуально, пока остальные учащиеся класса решают задачи на повторение.
На этапе повторения новое знание включается в систему знаний, а также решаются задания, обеспечивающие непрерывность развития содержательно‑методических линий курса. Так, на рассматриваемом уроке умножение многозначного числа на однозначное встречается при решении текстовых задач № 4–5, стр. 2, в уравнении № 6, стр. 2 и при работе с буквенными выражениями в № 7, стр. 2. Далее в задании № 8, стр. 2 повторяется правило порядка действий в выражениях и отрабатываются вычислительные навыки. В № 9, стр. 2 повторяются действия с многозначными числами, в № 10–11, стр. 2 – понятия равенства и пересечения множеств, которые связываются с рисованием геометрических фигур и перебором вариантов, а в № 12, стр. 2 предлагается логическая задача. Учитель на уроке введения нового знания выбирает для оставшихся 5–10 минут урока из этих заданий те, в которых учащиеся его класса испытывают больше затруднений.
Учитель на уроке введения нового знания выбирает для оставшихся 5–10 минут урока из этих заданий те, в которых учащиеся его класса испытывают больше затруднений.
Сделать этот выбор более осознанным и обоснованным позволяют «Электронные приложения к учебникам».
С другой стороны, методическим приемом, который позволяет существенно увеличить число решенных в классе примеров без перегрузки детей, является решение задач по выбору учащихся. Так, например, на данном уроке учитель может предложить учащимся на этапе повторения решить по выбору одно из заданий № 5–9, стр. 2. Учащиеся в течение 3–4 минут решают по одному выбранному ими заданию, а затем проговаривают их решение в течение следующих 5 минут. Таким образом, все задания воспроизведены в памяти детей, т. е. цель повторения достигнута. При этом в классе создается атмосфера психологической комфортности, так как каждый ребенок решает задание, которое он выбрал сам, а значит, то, которое ему больше понравилось. Задачи по выбору можно предлагать и для домашней работы.
Задачи по выбору можно предлагать и для домашней работы.
При подведении итога урока учитель обсуждает с учениками вопросы:
– Что нового узнали? (Научились умножать любое многозначное число на однозначное.)
– Какое математическое свойство для этого использовали? (Распределительное свойство умножения.)
– Кто уже чувствует себя уверенно в решении новых примеров?
– Что повторили? Что больше всего понравилось?
– Кто сегодня нам помогал на уроке?
– Как оцениваете свою работу?
Для домашней работы можно предложить учащимся придумать и решить свой пример на умножение многозначного числа на однозначное, решить задачу № 4, стр. 2 и по желанию – одно из заданий № 10–12, стр. 2. Таким образом, обязательное задание не займет у обучающихся больше 10–15 мин самостоятельной работы. При таком подходе исключена перегрузка детей, каждому из них обеспечивается возможность успешного усвоения необходимого минимума, и в то же время каждому предоставляется возможность обучения на высоком уровне за счет активного включения в деятельность на уроке и решения дополнительных развивающих заданий.
На уроках 7–8 рассматриваются более сложные случаи умножения многозначного числа на однозначное и случаи умножения круглых чисел, сводящиеся к ним. Так, в № 1, стр. 6 учащиеся распространяют на множество многозначных чисел изученное ранее правило: чтобы умножить круглые числа, надо выполнить умножение, не глядя на нули, а потом к полученному произведению приписать столько нулей, сколько в обоих множителях вместе. На основании этого правила при записи умножения круглых чисел в столбик для удобства вычислений нули мысленно отбрасываются и полученное однозначное число записывается в разряде единиц многозначного множителя:
На последующих уроках умножение многозначного числа на однозначное отрабатывается в основном в процессе выполнения проверки примеров на деление.
На уроке 8 рассматривается новый тип задач – задачи на нахождение величин по их сумме и разности. На основе предметных действий с моделями полосками ученики догадываются, что при вычитании из суммы двух чисел их разности получается удвоенное меньшее число, а при сложении суммы и разности – удвоенное большее число. Поэтому решить задачу, например, № 1, стр. 8 можно двумя способами:
Поэтому решить задачу, например, № 1, стр. 8 можно двумя способами:
Для этапа первичного закрепления предназначены задания № 3–4, стр. 8–9, а для этапа самостоятельной работы с самопроверкой в классе – № 2, стр. 8. Дома можно предложить им придумать и решить свои задачи на нахождение величин по их сумме и разности.
На всех данных и последующих уроках особое внимание уделяется комментированию решения уравнений по компонентам действий (№ 6, стр. 2; № 6, стр. 4; № 6, стр. 9; № 7, стр. 18; № 5, стр. 20; № 4, стр. 25 и т. д.). Это связано с подготовкой детей к изучению темы «Уравнения» на уроке 27 данной части учебника. К этому времени обучающиеся должны не только уметь на автоматизированном уровне верно находить неизвестные компоненты действий, но и комментировать решение по образцу, приведенному на стр. 77 учебника.
На уроках 9 – 12 формируется умение делить многозначные числа на однозначные и делить круглые числа, сводящиеся к делению на однозначное число, умение делать проверку деления умножением, а также повторяются и закрепляются нумерация, сложение и вычитание многозначных чисел, умножение многозначного числа на однозначное, решение текстовых задач. Учащиеся решают уравнения с комментированием по компонентам действий, повторяют понятие периметра треугольника, понятие числового луча, действия с единицами длины и массы, читают и записывают выражения.
Учащиеся решают уравнения с комментированием по компонентам действий, повторяют понятие периметра треугольника, понятие числового луча, действия с единицами длины и массы, читают и записывают выражения.
При изучении внетабличного деления в пределах 100 учащиеся знакомились с правилом деления суммы на число. Сейчас это правило используется для построения алгоритма деления многозначного числа на однозначное. В итоге обсуждения учащиеся должны выявить и осмыслить основную идею, основной принцип деления многозначных чисел: сначала делится более крупная счетная единица, затем остаток дробится и делится следующая по величине счетная единица и так далее до конца. Новый материал вводится в обучение деятельностным методом.
На уроке 9 на этапе актуализации знаний с учащимися нужно вспомнить взаимосвязь между умножением и делением (a : b = c ⇔ b · c = a, b 0), алгоритм деления с остатком и правило деления суммы на число, распространив его, как и в предыдущем случае, на сумму трех и более слагаемых.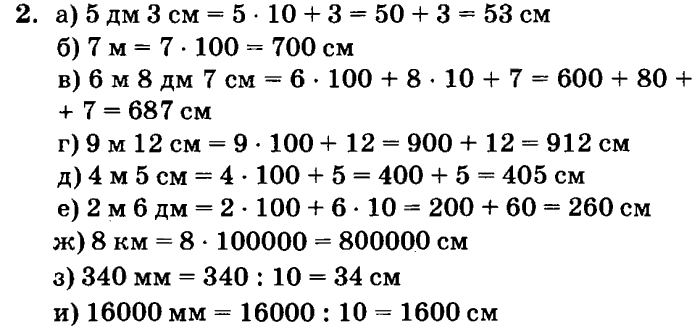
На этапе постановки проблемы детям можно предложить в течение 2–3 минут в тетрадях в клетку самостоятельно решить примеры «по частям», т. е. используя правило деления суммы на число, и выявить в них закономерности:
Учащиеся могут заметить, что:
1) все примеры – на деление;
2) делимое увеличивается, а делитель не изменяется;
3) с увеличением делимого частное увеличивается;
4) если делимое увеличивается в 10 раз, то и частное увеличивается в 10 раз.
При решении последнего примера обычно возникает затруднение, которое мотивирует поиск нового способа действий (если и последний пример выполнят все ученики, можно попросить их найти лишний пример).
Далее учитель подводит учащихся к выявлению существенного для данного урока признака отличия последнего примера от предыдущих: первые четыре примера сводятся к делению двузначного числа на однозначное, а в последнем примере – деление трехзначного числа на однозначное. Этот признак отличия учащиеся должны проговорить вслух.
Этот признак отличия учащиеся должны проговорить вслух.
Таким образом, ставится цель урока – установить, как делится многозначное число на однозначное. (Если затруднений в решении последнего примера у обучающихся не возникнет, слово установить заменяется словом обосновать – ведь подобные примеры в классе ранее не рассматривались.)
На этапе «открытия» нового знания детям вначале предоставляется возможность выбрать метод рассуждений. Задания, рассмотренные в начале урока, должны сориентировать их на выбор правила деления суммы на число, распространенного на случай нескольких слагаемых. Для подбора слагаемых для вычисления частного 536 : 4 можно использовать графическую модель. Учитель рисует ее на доске, а учащиеся – в тетради:
Рассматривая ее, ученики должны догадаться, что для нахождения частного вначале надо разделить сотни (коробки), затем оставшуюся сотню перевести в десятки и делить все имеющиеся десятки (пачки) и, наконец, оставшийся десяток раздробить в единицы (штуки) и делить единицы. В менее подготовленных классах поиск решения целесообразно сопровождать не только графическим моделированием, но и предметным – работой с конкретными коробками, пачками и единицами предметов.
В менее подготовленных классах поиск решения целесообразно сопровождать не только графическим моделированием, но и предметным – работой с конкретными коробками, пачками и единицами предметов.
Получившиеся группы обводятся овалами – это «удобные слагаемые»:
Из приведенных рассуждений следует, что каждый получил 1 сотню, 3 десятка и 4 штуки, или 134 штуки предметов. На математическом языке проведенные рассуждения можно записать так:
536 : 4 = (400 + 120 + 16) : 4 = 400 : 4 + 120 : 4 + 16 : 4 = 100 + 30 + 4 = 134.
Эта цепочка преобразований записывается в тетрадь, и еще раз проговаривается полученный вывод: чтобы разделить многозначное число на однозначное, можно делимое разбить на сумму «удобных» слагаемых и делить «по частям», то есть по правилу деления суммы на число.
Применение этого способа действий весьма ограничено, но проведенные рассуждения помогут учащимся в дальнейшем осмыслить общий принцип деления многозначных чисел. Для перехода к делению углом надо показать им неудобство построенного способа действий, предложив, например, найти частное 11 768 : 4.
Для перехода к делению углом надо показать им неудобство построенного способа действий, предложив, например, найти частное 11 768 : 4.
Понятно, что попытки найти «удобные» слагаемые вряд ли закончатся успехом, и тогда можно попросить детей еще раз вернуться к рисунку:
– Рассмотрите, с каких единиц мы начинали деление – с мелких или с крупных? (С крупных.)
– Конечно, ведь удобнее сначала раздать более крупные счетные единицы – коробки. Но вот у нас 1 коробка осталась, что нам пришлось сделать? (Достать пачки и делить уже пачки.)
– Правильно, нам пришлось раздробить сотни в десятки. А когда и десятки у нас закончились, что мы сделали? (Стали делить единицы.)
– Кто теперь догадается, как можно делить любое многозначное число, не подбирая слагаемые? (Делить сначала самые крупные счетные единицы, затем остаток дробить и делить более мелкие единицы.)
На доске в процессе беседы учитель кратко записывает суть выполняемых преобразований:
1) 5 с. : 4 = 1 с. (ост. 1 с.)
: 4 = 1 с. (ост. 1 с.)
2) 13 д. : 4 = 3 д. (ост. 1 д.)
3) 16 ед. : 4 = 4 ед. Итак, 536 : 4 = 134.
Аналогично записывается решение примера 11 768 : 4, предложенного учителем:
1) 11 т. : 4 = 2 т. (ост. 3 т.)
2) 37 с. : 4 = 9 с. (ост. 1 с.)
3) 16 д. : 4 = 4 д.
4) 8 ед. : 4 = 2 ед. Итак, 11 768 : 4 = 2942.
Таким образом, поставленная проблема решена: найден общий способ деления многозначного числа на однозначное. Он заключается в делении с остатком возможно более крупных счетных единиц и последовательном переходе к делению более мелких счетных единиц. Однако остается проблема записи деления. На вопрос учителя: «Удобная ли запись деления?» – ответ всегда одинаковый: неудобная, громоздкая. Тогда можно предложить учащимся попробовать придумать свою запись, более короткую и удобную. Для этой цели лучше использовать первый пример – 536 : 4.
Только после того как дети предложат свои версии, следует показать им «свернутый» способ записи приведенных рассуждений – уголком, и прокомментировать его:
Проверку деления удобно делать умножением на основании взаимосвязи:
Так, для проверки выполненного деления можно число 2942 умножить на 4.
Учитель обращает внимание учащихся на то, что при комментировании примеров надо вначале указать первое неполное делимое, потом определить число цифр в частном, а затем рассказать, как находятся цифры в каждом разряде частного. При этом надо постоянно помнить о том, что на каждом шаге мы фактически выполняем деление с остатком, и поэтому получаемые остатки должны быть меньше делителя. Проверку решения удобно делать умножением.
Алгоритм письменного деления фиксируется с помощью блок-схемы:
Проблема разрешена.
Для проведения этапа первичного закрепления можно использовать задания № 3–6, стр. 11–12, которые решаются с проговариванием в громкой речи. В № 3 учащиеся находят частное всеми тремя рассмотренными способами. В № 4 внимание детей еще раз фиксируется на том, что остаток от деления всегда должен быть меньше делителя, проговариваются основные этапы деления многозначного числа на однозначное, выделенные в рамке на стр. 11. Примеры № 5–6 записываются в тетради в клетку и решаются по выбору. Здесь возможно комментирование в паре, в группе, создание игровых ситуаций. Достаточно, если каждый ребенок решит 2–3 примера. Параллельно проговаривается способ проверки деления умножением, зависимость между компонентами деления.
11. Примеры № 5–6 записываются в тетради в клетку и решаются по выбору. Здесь возможно комментирование в паре, в группе, создание игровых ситуаций. Достаточно, если каждый ребенок решит 2–3 примера. Параллельно проговаривается способ проверки деления умножением, зависимость между компонентами деления.
Задание № 2, стр. 10 целесообразно использовать на этапе самостоятельной работы с самопроверкой в классе. Оно менее сложное, чем примеры, решенные на предыдущем этапе урока, и содержит наглядную опору, которая поможет обучающимся лучше представить каждый этап деления.
На этапе повторения по выбору можно решить задания № 7 (а), стр. 12 и №9 (а), стр. 12.
При подведении итога урока обсуждаются вопросы:
– Что нового узнали? (Научились делить многозначное число на однозначное, записывать деление «углом».)
– Какой прием используется для устного деления? (Деление «по частям».)
– С каких единиц начинаем письменное деление? (С самых крупных. ) А потом? (Делим по очереди более мелкие единицы.)
) А потом? (Делим по очереди более мелкие единицы.)
– Кто сегодня нам хорошо помогал?
– Кто доволен своей работой?
– Что повторили? Что больше всего понравилось?
В домашней работе можно предложить учащимся самостоятельно составить и решить пример на деление трехзначного числа на однозначное, построить его графическую модель и выполнить деление тремя способами по аналогии с тем, как это сделано в учебнике. Кроме того, решить по собственному выбору одно из заданий № 7 (б), 9 (б), стр. 12. В качестве дополнительного задания, которое выполняется по желанию, – одно из заданий №8, 10, стр. 12.
На последующих уроках рассматриваются более сложные случаи деления: делимое содержит большее число цифр (урок 10), в частном получаются нули в середине и на конце (уроки 11–13).
Чтобы переварить знания, надо поглощать их с аппетитом.
(А. Франц)
Желаем Вам удачи и творческих успехов!
Мы вместе, значит, у нас все получится!
| Математика, 3 класс Тема: Единицы длины. Цель: систематизировать знания детей о единицах длины. Задачи: • образовательные: — закрепить знания детей о соотношениях измерения длины, умения выражать величины в разных единицах измерения длины: — закрепить знания о действия с многозначными числами, умения решать текстовые задачи; • развивающие: — развивать речь, память, логическое мышление, внимание; • воспитательные: — воспитывать интерес к математике. оборудование: ноутбук, проектор, карточки (устный счет, дополнительные задания) Этапы урока Деятельность учителя и обучающихся I Орг.момент II Актуализация знаний — На экране будут появляться числа, вы должны найти среди примеров *, развешанных в классе, тот, ответом которого будет это число. Устный счёт: слайд 2, 70*9 480:8 420:6 160:40 60*3 300м*10 — Каждому числу присвоена буква слайд 2 — Поставьте ответы в порядке возрастания, и вы узнаете зашифрованное слово слайд 2 — Это то, за чем мы каждый день приходим в школу. — Какой пример отличается от остальных? (300м*10) слайд 3 — Чем? (действие происходит с именованными числами) — Какую единицу измерения вы здесь видите? (метры) — Что измеряется в метрах? (длина) — Какую более крупную единицу длины вы знаете? (км) — Выразите получившийся ответ в км (3000м=3км) сл 3 -Выразите в самой маленькой единице измерения длины. (3000м=3000 000 мм) слайд 3,4 -Почему возникло затруднение? (Чтобы ответить на этот вопрос мы должны установить соотношение между единицами длины) III Постановка темы, задач урока — Какова тема урока? (единицы длины) слайд 3,4 — Какая задача стоит перед нами? (закрепить знания о соотношении между единицами измерения длины) IV Изучение нового — В этом нам поможет таблица. слайд 3,4 — Сколько в 1 см мм? (1см=10мм) — Сколько в 1 дм см, мм? (1дм=10см=100мм) — Сколько в 1 м дм, см, мм? (1м=10дм=100см=1000мм) — Сколько в 1 км м, дм, см, мм? (1км=1000м=10000дм=100000см=1000000мм) — Какое действие выполняли при переходе к меньшим меркам? (умножали на 10, 100, 10000,100000,1000000) — Так сколько же в 3 км мм? (3 км=3000000мм) — Какое противоположное действие действию умножения? (деление) — При переходе к более крупным единицам измерения, какое действие будем выполнять? (делить на 10, 100, 1000, 10000, 100000, 1000000) V Первичное закрепление — Применим эти знания в следующем упражнение слайд 5+таблица — Послушайте, как правильно надо рассуждать: в 1 дм 10 см, значит 5*10, будет 50, да еще 3 см, получается 53 см Вырази в см 5дм3см=53см 7м=700см 6м8дм=680см Вырази в мм 64см=640мм 1дм5см=150мм 5м82см=582мм Вырази в м ** для детей с более быстрым темпом работы предусмотрены карточки с дополнительными заданиями. ** Выполни действия: 56 см 2 мм + 3 дм 4 см 4 км 25м – 510 м 5 м 4 дм – 25 дм 7 см Выполни действия: 56 см 2 мм + 3 дм 4 см 4 км 25м – 510 м 5 м 4 дм – 25 дм 7 см Выполни действия: 56 см 2 мм + 3 дм 4 см 4 км 25м – 510 м 5 м 4 дм – 25 дм 7 см Выполни действия: 56 см 2 мм + 3 дм 4 см 4 км 25м – 510 м 5 м 4 дм – 25 дм 7 см Сравни: 5 км 30 м 5300 м 6 дм 50 мм 65 см 9 м 46 см 94 дм 6 см 1800 мм 1 м 8 см 1 м 35 см 1350 мм Сравни: 5 км 30 м 5300 м 6 дм 50 мм 65 см 9 м 46 см 94 дм 6 см 1800 мм 1 м 8 см 1 м 35 см 1350 мм Сравни: 5 км 30 м 5300 м 6 дм 50 мм 65 см 9 м 46 см 94 дм 6 см 1800 мм 1 м 8 см 1 м 35 см 1350 мм Сравни: 5 км 30 м 5300 м 6 дм 50 мм 65 см 9 м 46 см 94 дм 6 см 1800 мм 1 м 8 см 1 м 35 см 1350 мм |
Единитсы длины. 3 класс. Петерсон
Конспект урока математики
Тема: Единицы длины.
Цели деятельности учителя: расширить и углубить знания учащихся о единицах длины; отрабатывать навыки преобразования именованных чисел в более мелкие единицы измерения и наоборот.
Планируемые результаты:
предметные: научатся переводить единицы изменения длины в другие единицы измерения; систематизировать знания детей о единицах измерения длины; уметь сравнивать, складывать и вычитать единицы длины.
личностные: научатся осознавать свои возможности в учении; смогут адекватно судить о причинах своего успеха или неуспеха в учении, связывать успехи с усилиями, трудолюбием.
метапредметные: умение доказывать свое мнение, проверять истинность высказывания, строить логическую цепочку рассуждений.
Тип урока: открытие нового знания.
Оборудование: Математика: 3 класс: Петерсон Л.Г., УМК «Перспектива», в 3 – х частях; презентация; проектор; компьютер; доска.
№ Этап урока
Метод и приемы Содержание урока. Деятельность учителя. Деятельность ученика УУД
1. Организационный момент Здравствуйте, ребята! Меня зовут Татьяна Леонидовна. Сегодня я проведу у вас урок математики. Приветствовать учителя. 2. Мотивационный
этап
Практический метод: математический диктант.
Словесный метод:беседа. Для начала давайте проведем математический диктант. Возьмите листочки на своей парте и напишите свою фамилию в правом верхнем углу.
Внимательно послушайте, если вы согласны с утверждением или высказыванием и хотите сказать «Да», то рисуете кружок, а если не согласны, то рисуете квадрат.
Всем понятно?
Математический диктант.
В числе 7 253 пять единиц второго класса.
За числом 12 379 следует число 12 380.
В числе 8 635 восемь единиц второго разряда.
Наибольшее пятизначное число 10 000.
Число 61 789 записано пятью разными цифрами.
Давайте сверим ваши ответы с эталоном на доске.
Рядом с каждым правильным ответом ставьте «+».
Кто не допустил ни одной ошибки?
У кого одна или две ошибки?
У кого больше двух?
Что это значит? (Необходимо еще повторить разрядные слагаемые.) Отвечать на вопросы учителя.
Сверять работу с эталоном.
К: планирование учебного сотрудничества с учителем и сверстниками.
Р.: контроль, коррекция, оценка.
3. Постановка учебной задачи и ее решение
Практич. метод: работа по учебнику
Словесный метод:беседа.
Прочитайте афоризм на слайде.
Никто не знает, каковы его силы, пока их не использует.
Как вы понимаете этот афоризм? Хотелось ли бы вам проверить собственные силы в учении, в познании нового?
Как тогда мы должны построить свою работу? (Определим, чего мы ещё не знаем и сами найдём способ)
Посмотрите на слайд и попробуйте самостоятельно выполнить это задание в тетради.
а) 5 дм 3 см = 50 см + 3 см = 53 см
г) 9 м 12 см = 900 см + 12 см = 912 см
ж) 8 км = 800 000 см
Сверьте свои записи с эталоном на доске.
Кто допустил ошибку? В каком месте?
Возникли ли у вас затруднения при выполнении это задания?
Давайте сделаем вывод. Как нужно переходить от больших мерок в меньшие? А из меньших в большие?
Теперь откройте учебник и посмотрите правило в рамочке на стр. 95.
Правильно ли мы с вами сделали вывод?
Послушайте шуточное стихотворение.
Филя и Муля – две умных собаки.Живут друг от друга они далеко.
Хоть быстры они – не то что раки!
Без друга быть долго не очень легко.И, чтобы разлук изменить состоянье,Решили измерить они расстоянье.Но сами решить — то задачу не могут!Позвали собачки Длину на подмогу.Спросили совета: «А как же нам быть?»Длина усмехнулась, зевнула, качнуласьИ стала от домика к дому ходить.Затем между ними она протянулась,А Филя и Муля глядят с изумленьем,И жаждут ответа они с нетерпеньем…Лежала Длина, от стыда не дыша,От горя не может подняться и встать.Она единиц измеренья не зналаИ не сумела себя сосчитать.
Как сформулируем тему нашего урока? (Единицы длины.)
Какую цель вы поставите сегодня на уроке? (Узнать о единицах длины.) Слушать учителя. Отвечать на вопросы.
Прогнозировать тему урока.
Ставить цель. П.: анализ, синтез, сравнение, обобщение, аналогия;
К: аргументация своего мнения.
К: выражение своих мыслей с достаточной полнотой и точностью.
Р.: целеполагание.
4. Физминутка. А теперь отдохнем и проведем физминутку. Повторяйте движения за героями на экране. Повторять движения за героями на экране. Л: установка на ЗОЖ.
5. Решение частных задач
Практич. метод: работа с учебником.
Словесный метод:беседа. Посмотрите на слайд. Что изображено наверху? (Единицы длины)
А что изображено ниже? Что обозначают эти числа? (Это соотношение между единицами длины)
А вы знаете единицы измерения?
Ученики вспоминают таблицу мер длины и устанавливают соотношения между единицами длины.
Посмотрите на слайд. Давайте ответим на эти вопросы.
Сколько в 1 километре метров, дециметров, сантиметров, миллиметров? (1 000 м, 10 000 дм, 100 000 см, 1 000 000 мм)
Сколько в 1 метре дециметров, сантиметров, миллиметров? (10 дм, 100 см, 1 000 мм)
Сколько в 1 дециметре сантиметров, миллиметров? (10 см, 100 мм)
Сколько в 1 сантиметре миллиметров? (10 мм)
Как мы переходим к меньшим меркам от больших? (Умножаем на 10, 100, 1 000)
Как мы переходим к большим меркам? (Выполняем деление именованного числа на 10, 100, 1 000)
Давайте сделаем вывод, какое действие выполняется при переходе к меньшим меркам, а какое – при переходе к большим меркам? (К меньшим меркам – умножение, к большим – деление)
Теперь посмотрите на номер 3. Что мы должны сделать в этом задании? (Выразить в миллиметрах)
Первый столбик выполним все вместе. Один ученик у доски.
а) 3 см 9 мм = 30 мм + 9 мм = 39 мм
б) 2 дм 5 см 7 мм = 200 мм + 50 мм + 7 мм = 257 мм
в) 8 дм 3 мм = 800 мм + 3 мм = 803 мм
Под буквой б) решает 1 вариант, а под буквой ж) второй вариант. Кто быстро и правильно выполнит это задание.
Сверьте свои записи с эталоном на доске.
Кто допустил ошибку? В каком месте?
Давайте сделаем вывод. Как нужно переходить от больших мерок в меньшие?
Посмотрите на следующий номер. Что мы должны сделать в этом задании? (Выразить в метрах)
Первый столбик выполним все вместе. Три ученика у доски, остальные в тетради.
а) 4 км 700 м = 4 000 м + 700 м = 4 700 м
б) 6 км 18 м = 6 000 м + 18 м = 6 018 м
в) 12 км 50 м = 12 000 м + 50 м = 12 050 м
Решите второй столбик самостоятельно.
Сверьте свои записи с эталоном на доске.
Кто допустил ошибку? В каком месте?
Давайте сделаем вывод. Как нужно переходить от больших мерок в меньшие? А из меньших в большие?
Переверните страницу и найдите номер 5. Нам нужно сравнить эти числа.
Что мы знаем о сравнении именованных чисел? (Чтобы сравнить именованные числа, необходимо преобразовать их в одинаковые единицы измерения.)
Давайте сравним эти числа.
Что больше 3 м 7 см или 6 дм 8 см? Почему?
А что больше 5 дм 30 мм или 53 см? Почему?
Что больше 9 км 300 м или 9 030 м? Почему?
Что больше 7 м 86 см или 78 дм 5 см? Почему?
Найдите номер 6. Прочитайте задание.
Давайте выполним это задание вместе у доски.
Два человека решают у доски.
Давайте сделаем вывод. Как нужно переходить от больших мерок в меньшие? А из меньших в большие?
Посмотрите на номер 7.
Давайте решим под буквой а) все вместе. Решение будем записывать в рамочке простым карандашом.
Прочитайте задачу. Что нам известно?
А можем мы сразу ответить на вопрос задачи? Почему? (Нет, потому что не знаем, сколько Петя прошел лесом.)
А мы можем это узнать? Каким действием? (Да, делением)
Зная сколько прошел Петя полем и лесом, можем ли мы ответить на вопрос задачи? Каким действием? (Да, можем. Сложением)
Запишем получившееся выражение в рамочку.
Если дети все понимают, остальное решают самостоятельно, если возникли затруднения, решаем все вместе.
Сверьте свои записи с эталоном на доске.
а) a + a: 2
б) b – c
в) n + (n + 5) + (n: 2)
г) (x – y): 20
д) a – (3 · b)
Кто допустил ошибку? В каком месте?
Давайте решим номер 8 все вместе.
Один ученик у доски.
Что нам нужно сделать? (Составить выражение и найти его значение.)
а) 208 400 – (18 000 – 9762) = 200 162
б) (720 048 – 97 256) – (36 809 + 250 249) = 335 734
в) (777 777 + 66 666) + (111 111 – 99 999) = 833 331
Записываем выражение на доске, а все остальные у себя в тетрадях.
Сколько действий в первом выражении? (2)
Как будем решать: в столбик или в строчку? (В столбик)
Как записываем числа в столбик? (Единицы под единицами, десятки под десятками, сотни под сотнями и так далее)
Сколько получилось? (200 162)
Сколько действий во втором выражении? (3)
Сколько получилось? (335 734)
Сколько действий в третьем выражении? (3)
Сколько получилось? (833 331) Отвечать на вопросы.
Сверять работу с эталоном.
Сверять работу с эталоном.
Слушать учителя. Отвечать на вопросы.
П.: анализ, синтез, сравнение, обобщение, аналогия
К: выражение своих мыслей с достаточной полнотой и точностью;
Р.: контроль, коррекция, оценка.
6. Итог урока. Рефлексия.
Практич. метод: лесенка успеха.
Словесный метод:беседа. Какую цель вы перед собой ставили? (Узнать о единицах длины.)
Удалось ли достичь цели?
Что нового вы узнали на уроке?
Теперь я предлагаю вам оценить свою работу на уроке. Положите перед собой «лесенку успеха». Покажите, на какой ступеньке вы находитесь в конце урока. Слушать учителя. Отвечать на вопросы.
Осуществлять самооценку.
П.: контроль и оценка процесса и результатов деятельности;
Л: самооценка.
Урок математики по теме «Метр. Таблица единиц длины», 2 класс
Урок математики во 2 классе.
Тема. Метр. Таблица единиц длины.
Тип урока: объяснение нового материала.
Цель урока:
Познакомить с новой единицей измерения длины – метром, учить измерять длины с помощью метра, сравнивать единицы длины, сформировать наглядное представление о метре.
Планируемые результаты:
Познавательные УУД:
Развитие мыслительных операций, логического мышления, математической речи.
Регулятивные УУД:
Умение определять и формулировать тему и цель урока с помощью учителя, планировать и контролировать свою деятельность , вносить коррективы и оценивать свою работу;
Коммуникативные УУД:
умение правильно строить речевое высказывание, слушать и понимать речь сверстников и учителя, отстаивать своё решение, работать в парах, группах, умение договариваться с одноклассниками.
Оборудование: сантиметровая лента, сантиметровая рулетка, классная линейка длиной 1м, плакат «Меры длины».
Ход урока
I. Организация учащихся на урок.
Ну-ка проверь, дружок,
Ты готов начать урок?
Все ль на месте?
Все ль в порядке?
Ручка, книжка и тетрадка?
А еще проверьте, детки,
Карандаш, линейку, ластик.
II. Актуализация знаний .
— С какой темой познакомились на предыдущем уроке? (Сотня.)
— Что нового узнали? (1сот.=10дес.=100ед.)
Эти знания нам понадобятся на сегодняшнем уроке.
Устный счёт.
Фронтальная работа.
Игра «Отвечай-ка»
На доске запись:
а) Самое маленькое трёхзначное число … (100)
б) На первом месте справа стоят …(единицы)
в) В числе 48 — … дес. … ед.
г) 1 дм = … см.
д) 1 с. — … ед.
е) 10 дес.- это …
2.Задача на смекалку
Аня выше Славы, а Света ниже Славы. Кто выше Аня или Света?
( Аня)
Ш. Самоопределение к деятельности.
Чтобы определить тему нашего урока, нам нужно прочитать шифровку.
Математическая шифровка
Р – 8+9-2 Т — 10-8+9
Е — 13+7 М — 6+8
Дети читают хором: Метр. Итак, тема нашего урока « Метр».
— Что вы знаете о метре? Какие еще единицы измерения длины вы знаете?
Учитель демонстрирует модель метра.
Это модель метра.
IV. «Открытие» детьми нового знания
— Сегодня вы сами всё расскажите о новой единице длины — метре, а для этого нужно провести исследования.
Практическая работа.
Работа в группах.
Задание для 1 группы.
Что измеряют в метрах?
— Измерить метровой линейкой:
а) длину и ширину стола.
б) длину и ширину классной комнаты.
— Сделайте вывод:
В метрах измеряют длину и ширину классной комнаты.
А что ещё можно измерить в метрах?
Рассматривание рисунков в учебнике с.13.
Задание для 2 группы .
Что такое метр?
— Измерьте длину классной линейки (1 метр):
а) в дециметрах;
б) в сантиметрах.
— Сделайте вывод:
1м = 10 дм
1м = 100см
Задание для 3 группы.
Метр на службе у человека.
— Вспомните, где человек использует метр.
Детям выдаются карточки с рисунками: рулон ткани, садовый участок, комната в квартире, аллея и др.
— Сделайте вывод:
(примерные ответы)
а) измерение ткани.
б) измерение длины садового участка.
в) измерение длины доски.
Общий вывод и запись на доске и в тетрадках:
1м = 10дм
1м = 100см
V. Физкультминутка
Танец «Буги –вуги».
VI. Первичное закрепление изученного материала.
Работа по учебнику:
1.№ 2, с . 13 письменно с комментированием в обычных тетрадях в клетку.
2. На сколько сантиметров 1м больше, чем 1 дм?
( 1м = 100см, 1дм = 10 см; 100- 10 = 90 см)
На сколько сантиметров 1 м больше 1 см?
( 100- 1= 99 см)
VII. Самостоятельная работа.
Цель: проверить усвоение единиц измерения длины
(учащимся раздаются карточки). Как вариант – работа в парах.
Уровень А
— Заполни пропуски, преобразуй единицы:
5дм 4см = …см
9м = …дм
3м 7дм = …дм
8дм = …см
1м 3дм = …дм
Уровень В
— Преобразуй именованные числа:
25дм = …м …дм
70дм = …м
40см = …дм
89см = …дм…см
24см = …дм …см
Уровень С
— Допиши недостающие наименования:
85 дм = 8…5…
5дм = 4дм 10 …
60см = 6…
5… = 50…
3м 2дм = 32 …
74дм = 7…4…
VIII. Физминутка.
Хлопай, мишка,
Топай, мишка,
Приседай со мной, братишка.
IX. Работа над пройденным материалом.
- Работа над задачей № 4 с опорой на памятку.
Памятка
Читаем задачу.
Называем условие (что известно).
Называем вопрос ( что надо узнать).
Записываем кратко, или выполняем рисунок, или схему, или чертёж, или записываем в таблицу.
Объясняем.
Решаем.
Называем ответ.
Выполняется краткая запись у доски:
1 книга – 40 с.
2 книга — ?, на 20 с. > ?
Решение записывается на доске.
40 + 20 = 60 ( с.) – во 2 книге.
40 + 60 = 100 ( с.)
Ответ: 100 страниц в этих двух книгах.
X. Рефлексия. Подведение итога урока.
— С какой новой единицей измерения длины познакомились на уроке?
— Что интересного узнали? Какое задание вам понравилось больше всего? Какое задание показалось трудным?
XI. Домашнее задание.
с.13 № 5.
Веб-страница Peterson — HYPERDOCS
Детский сад HyperDocs
K-5 HyperDocs — отлично!
HyperDocs K-6-го класса
HyperDocs 1-го класса
HyperDocs 1-го класса на Padlet
Первый класс — основная идея
Государство и гражданство 2-го уровня
HyperDocs 2-го уровня
Выводы 2-го класса
Литературная тетрадь для 2-го класса HyperDoc
Интерактивная языковая тетрадь 3-го класса HyperDoc
3-й класс: басни, сказки
HyperDocs 3-го уровня
Жизненный цикл 3-го уровня HyperDoc
Солнечная система 3-го класса
Уровень HyperDocs
HyperDocs 4-го класса
HyperDocs 5-го класса
5-й класс: Характеристики организмов HyperDoc Choice School 9000 9000 9000 9000 9000 9000 9000 9000 Всемирная история 7-го класса
HyperDocs 7-9-го классов
Вторичные HyperDocs
9000
100-й день в школе
Надежды и мечты
Еще одна Padlet HyperDocs — Хорошо!
Дисковая папка HyperDocs
Давайте сделаем Hyperdoc
Добавление дробей
American Отчет о животных Thinglink
Искусство преподавания с HyperDocs: уроки, ориентированные на студентов, которые вдохновляют на любопытство и творчество
Искусство: Великие художники
Искусство
— Ren Art Study Google SlidesArt: SumoPaint + Thinglink Plant Project — Google Slides
Изгнание скуки: использование гипердок в начальном классе
Стать опытным учеником
Будьте законными и справедливыми
Ресурсы Breakout EDU HyperDoc
Breakout HyperDoc Resources
Цифровые изображения
Первые дни в школе HyperDocs
Иностранные языки: Испанские каникулы HyperDoc
Знакомство со своим классом Постановка целей Благодарность #Hyperdoc Использование Answer Garden — Google Docs 9000 Mindset 02 Надежды и мечты HyperDoc Как улучшить уроки с помощью Google HyperDocs Как HyperDocs могут трансформировать ваше обучение — Podacher
Шаблоны HyperDoc
HyperDocs Beyond HyperLinks
HyperDocs Mission Control
Hyperdocs
Сообщество Google+ в Google+Hyperdocs и самостоятельное обучение
Исследование и критическое мышление — Google Slides
ISTE Standards and HyperDocs Plan
K-1 Be Kind Online Resources
Language Arts HyperDocs
Lang Arts: Обзор заглавных букв / пунктуации Hyperdoc — Google Docs
Language Arts: — Английский язык для средней школы
Lang Arts: One Little Word — общий шаблон
ArtsЧитать вслух Шаблон HyperDoc
Искусство языка: Сличение и метафора
Лит .: Точка зрения автора
Lit — книга
Лит .: Благодаря Винну Дикси HyperDoc
Лит .: Биографические исследования плакатов HyperDoc — Хорошо!
Лит .: Cinquain Poetry
Лит .: Персонаж, настройка, сюжет
Лит .:
Лит .: Crenshaw
Лит .: Дневник Анны Франк HyperDoc
Лит .: E.B. White
Лит .: ELA HyperDoc
Лит .: Эрик Карл Автор исследования
Лит .:
Литера: Басни HyperDoc
Литера: Басни, сказки и сказки 000
Лит .: Проект бесплатных стихов
Лит .: Дар волхвов
Лит .:
Лит .: 90 004 Греческая мифология
Лит .: Поэзия хайку
Лит .: Поэзия хайку
000 9000 9000 9000 to Hyper Doc a Novel
Литература: ЗАДАЧНЫЕ ПЛАТЫ HYPERDOCS LITERACY И ЦИРКИ СЧИТЫВАНИЯ FLIPGRID
Литера: 9000 9000 9000 Introye to Catcher to the Crucible
Лит .: Остров Голубого Дельфина HyperDoc
Лит .: Johnny Appleseed
Lit4 с Google Earth
Лит .: Сон в середине лета Pre-Rea ding HyperDoc Activity Board
Литература: Повествовательная запись HD: черновик, пересмотр и публикация
Литера: Novel HyperDocs — многие 000
Лит .: Доска выбора новых проектов
Лит .: Pax
Лит .:
Лит .: Poetry Unit
Лит .: Polar Express
Лит .: Литература для чтения — 2н. d Оценка
Литера: Reflect and Recharge: конец семестра
Литера: Road Not Taken
Thunder Литера:
Лит .: Ромео и Джульетта Запуск HyperDoc — Google Документы
Лит .: Ромео и Джульетта
Джульетта
Лит .: Женщины Шекспира — Google Slides
Лит .:
Лит .: Story Elements
Лит .: Story Elements
Lit Magic: 000 Sylvester Lit Magic: Sylvester Tales of Fourth Grade Nothing Роман — Джуди Блюм
Лит .: The Crucible
Лит .: The Giver
Giver HyperDoc
Лит .: Маленький дом
Лит .: Аутсайдеры HyperDoc Resources
Литт: 000 000
Лит: Понимание американских легенд HyperDoc
Лит .: Дикий робот
Лит .: Что такое поэзия?
Math HyperDocs — Peterson
Math HyperDocs
Math: Math HyperDoc 9000 9000 9000 9000 9000 000 HyperDoc 9000 на Padlet
Математическая 6 Обзорная плата HyperDoc
Math HyperDocs List
Math HyperDocs
Математика: Сложение и вычитание к 12
Математика: Сложение фактов к 20 000 000 Дроби
Математика: Сложение
Математика: Площадь треугольника
Математика: Системы координат Математика 000 Математика 000
до 120Математика: Комбинации монет для создания доллара
Математика Сравнение чисел со 100
Математика:
различных типов треугольников : Десятичные дроби
Математика: Эквивалентные дроби
Математика: Фактические дни — Математика
Первые
9000 Десять кадров
Математика: дроби
Математика: Дроби Game Board
Математика: Геометрическое мышление — четырехугольники
Математика: , кодирование и измерения 50004 — геометрия
Math HyperDocs — EdTech Training
Math: Знакомство с полигонами HyperDoc
Math: 0003 0003 000 Google Docs
Math: Давайте узнаем об умножении
Math: Путь обучения измерениям
Математика: Mult iplication Fraction Game Board
Math: Percents
Math: Pi Day
Math: 000 000 000 000
Math: Place Value
Math: Обзор Place Value
Math: Place Value Game Board
Математика: Полигоны
Математика: Радиус и диаметры окружностей
Математика: Rational Number System
Математика: Атрибуты формы HyperDoc
Математика: Вычитание
Математика: Решение уравнений HyperDoc — 000
Математика: Вычитание чисел
Математика: Десятки и единицы
Математика:
HyperDocs средней школы
HyperDocs средней школы — STJ
Mr.Macs Menu Действия
Музыка: Обучение музыке
Музыка: Woodwind HyperDoc
Профессиональное развитие:
Список HyperDocs для разработчиков
Профессиональные разработки: Создайте команду LEGO
Science: 3 состояния материи
Science: Science Force Наука: HyperDocs 7-го класса
Science: HyperDocs 8-го класса
Science HyperDocs
GOOD
Science: Hyper Docs Science Примеры
Science: Animal Adaptations
Science: 000 Animal Cells
Наука: Среда обитания животных HyperDoc
Наука: Отчет о животных ThingLink HyperDoc
Наука: Биология: Клетки — структура и функции
Наука: Биомы HyperDoc
Наука: Cells HyperDoc
Наука: Характеристики Совета по выбору организмов
Наука: Химические реакции
oc2s oc4 Наука: Классификация животных HyperDoc
Наука: Начало облаков
Наука: Пищеварительная система HyperDoc
Наука: Земля в действии
Наука: Земля в действии: Погода
s и вулканы
Наука: Земные системы и процессы
Наука: Электричество
Наука: Электроника потрясающая! — 2-недельный курс
Наука: Энергия
Наука: Изучение водных ресурсов — Google Slides
Science4 Science: — поделиться — Google Docs
Science: Fall Leaves Science / Literacy HyperDoc
Science: Five Senses HyperDoc
Наука: Генетика
Наука: Глобальное потепление
Наука: Google Earth Connections to Ecosystems and Ecology
Sc ience: Насколько велика Вселенная
Наука: Соединения в теле
Наука: Жизненные циклы K-1: план урока бабочки — аналогично — аналогично
Science: Интернет-ресурсы урока бабочек K-1
Science: Жизненные циклы K-1: план урока лягушек
Science: K-1 Ресурсы
Наука: Изучение погоды — 5 класс
Наука: Жизненный цикл дерева — Повествование о жизни HyperDoc
Наука: Жизненный цикл HyperDoc
Наука: Жизненный цикл обучения
Наука: Жизненный цикл звезды
Наука: Микроскоп
000 000
Наука: Законы Ньютона — Google Docs
Наука: Одно дерево, один год
Таблица
Наука: Периодическая таблица / элементы HyperDoc Fifth Grade — Google Docs
Наука: Фазы Луны
000 Наука
Наука: Клетки растений и животных
Наука: Рост и выживание растений
Наука: Plant HyperDoc
Наука: фотосинтез и дыхание
Наука: Жизненный цикл тыквы
Наука: Быстрые изменения на поверхности Земли, вулканы , землетрясения , землетрясения,
Наука: Камни и полезные ископаемые
Наука: Простые машины — 4-й класс
Наука: 000 000 HyperDoc6 Солнечное затмение
Наука: Солнечная система HyperDoc
Наука: Space Explorer HyperDoc
Наука:
Наука: Торнадо
Наука: Вулканы, землетрясения и плиты Тектоника 000
Наука: Погода
Наука: Погода HyperDoc
Наука: Что вы делаете?
Социальные исследования HyperDocs
Социальные исследования HyperDocs
So Studies: Age of Exploration
So Studies: Удивительная гонка по штатам
So Studies: American Revolution
So Studies: Видео американского правительства на YouTube
So Studies: Авраам Линкольн и Джордж Вашингтон
So Studies: Американская революция
American Symbols
Так Исследования: 9 0005 Разделенная нация 1846-1861 — Часть 1
Итак, Исследования: Нация Разделенная — Часть II
Итак Исследования: Древний Египет HyperDoc
Так Исследования: Статьи Конфедерации
Так Исследования: Законопроект
Mining the Miner’s — Google Slides
So Studies: Colonial Williamsburg Hyperdoc — Google Docs
So Studies: Помощники сообщества
Гражданская война
Итак Исследования: Гражданская война HyperDoc
Итак Исследования: Была ли гражданская война неизбежна?
So Studies: Civil War — KWHLAQ
So Studies: Civil War Part I HyperDoc
So Studies: II II
So Studies: Colonial Times HyperDoc
So Studies: Community Helpers HyperDoc
So Studies: Конституция и рабство
Хлопковый джин и как он изменил жизньSo Studies: Декларация независимости
So Studies: Декларация независимости Slide Deck Hyperdoc — Google Slides
So Studies: Digital Road Trip USA — ОТЛИЧНО!
So Studies: Economic Theory
So Studies: Выборы
So Studies:
So Studies: Исполнительный орган правительства HyperDoc
So Studies: Explorer Technology Resources
So Studies4 Маршруты
So Studies: Исполнительная ветвь
So Studies: Fire Safety HyperDoc
So Studies:
So Studies: Французская революция
So Studies: Основание и формирование правительства
So Studies: Gold Rush
So Исследования: Правительство: Краткое введение
So Studies: Heading West
География So Studies Список HyperDocs
Социальные исследования: Holiday HyperDoc
So Studies: Holiday HyperDocs
Социальные исследования Google Holiday Социальные исследования Google Holiday
Так Исследования: Holocaust HyperDoc
So Studies: Родина: Древняя Греция и Рим
So Studies: Закон о законах
История и география
So Studies: Загадки истории: Древний Египет
So Studies: Иммигранты 1880-х годов
So Studies: Landforms 2-й класс
So Studies: Наследие Древней Греции HyperDoc — Google Docs
Законодательные исследования
So Studies: Льюис и Кларк
So Studies: Откройте для себя новые земли с Льюисом и Кларком — Хорошо!
So Studies: Откройте для себя новые земли с Льюисом и Кларком — Google Presentation
So Studies: Картирование колоний
, Младший
So Studies: Midnight Ride of Paul Revere HyperDoc
So Studies: Основные темы гражданского и государственного управления HyperDoc
So Studies: MLK Jr — Google Docs
So Studies: Коренные американцы
So Studies: 9000 000
So Исследования: Национальные парки Hyperdoc gr3 — Google Docs
So Исследования: Северо-Западная территория
Северо-Западный край
Социальные исследования: The Midnight Ride of Paul Revere
So Studies: Pearl Harbor HyperDoc 9000 9000 9000 9000 9000 Google Slides So Studies: Pioneer HyperDoc
So Studies: Plantations and Slavery Spread
So Studies: Настоящая история Пола Ревера
Т. Исследования: Фигурки и сражения за независимость
Исследования: Дорога в Лексингтон и Конкорд
Так Исследования: Через мои глаза — Руби Бриджес
So Studies: Подписание Декларации независимости
So Studies: Silk Roads
South
So Studies: Shays’s Rebellion
Социальные исследования: Super Awesome State Research
So Studies: 000 oc6 Gustto4000 So Studies: Налог, чаевые, комиссия — C hoice Board
So Studies: Три ветви власти
So Studies: This is ME HyperDoc
So Studies:
The World TraditionsSo Studies: Trail of Tears
So Studies: Три ветви правительства
So Studies: Underground Railroad Hyperdoc 9000 9000 9000 9000 So0006 9000 Исследования: Символы США — Google Slides
Так Исследования: Конституция США — полный блок
Так Исследования: Конституция США
So Studies: USA Regions
So Studies: US Symbols HyperDoc — K
So Studies: What a Wonderful World 9000 — Earth6 9000 So Studies: Где в США
Социальные исследования: Westward Expansion
Social Studies: Westward Expansion — хорошо!
Итак, исследования: Что такое сообщество? HyperDoc
Итак, исследования: Что такое место? — общественные науки
So Studies: Всемирная история
Испанский: Repaso HyperDoc
Tech: Tech: Your Own Adventure
Техника: Киберзапугивание
Техника: Кибербезопасность
Техника: Цифровая гражданственность и кодирование 9000 9000 9000 9000 Цифровые технологии и кодирование 9000 9000 Hyper Doc4000 Citizenship SuperHero Hyper Doc
Техника: Цифровой след
Техника: Выбор Google и Chromebook HyperDo
Google Google
Техник: Google F orms — Feel the Force
Tech: Green Screen Magic HyperDoc
Tech: Час кодирования / Введение в кодирование
Техника: Введение в кодирование / Час кода K-2 — Google Slides
Техника: Знакомство с Chromebook — Учителя HyperDoc
Tech: K-1 Ресурсы онлайн-урока по безопасности
Tech: Let’s Explore Technology Tech: Keyboarding Game Board
Tech: Multimedia Text Sets + Google Docs = HyperDocs
Tech: Rocky Tech Guy — HyperDocs
Tech: Show What You Know BINGO
Tech: Scratch Programming HyperDoc
Tech: Ресурсы для скринкастинга
Tech: Screencastify HyperDoc
Tech: Стратегии поиска
Техника: Советы и приемы для надстроек Google Docs HyperDoc
Техника: Tech 2000200020002
Визуальная грамотность
Словарь: Ключевые слова, которые нужно сделать HyperDoc — Google Slides
9000 HyperDoc Worlds 9000 Wild7 9000 HyperDoc 9000 9000 World Список
HyperDoc: Базовый шаблон плана урока HyperDoc
Написание: Сравнение и сопоставление эссе HyperDoc
9000 HyperDoc HyperDoc: Документы: использование надстроек HyperDoc
HyperDoc: Диск для использования HyperDocs
Writing: Design a Simile6 000 000300030003 в Google Написание: Эссе s
Написание: Грамматический список HyperDocs
Написание: Грамматика HyperDoc
Написание
Написание: Сличений / метафор HyperDoc
Написание: Snapchat Повествовательное написание
000 000 000 000 000 HyperDocs: Расширение инструментов Google с помощью надстроек HyperDoc
HyperDoc: Любимые инструменты HyperDoc !!!
HyperDocs — рамки для 4 C в аудиториях, ориентированных на учащихся
HyperDocs из онлайн-курса HyperDoc
HyperDocs by Subject 000
ДокументыHyperDoc: Hyper Docs Speaker
HyperDoc: Шаблон HyperDocs — хорошо!
HyperDoc: Шаблоны HyperDocs
HyperDoc: HyperDoc Tools
HyperDoc: Doc
HyperDocs: HyperDocs по темам
HyperDoc: Hyper для Hyper Docs
HyperDocs HyperDoc: HyperDoc: Gallery Wall — ОТЛИЧНО!
HyperDoc: HyperDoc HyperDoc
HyperDoc: Hyperdoc Ideas
HyperDoc4:
HyperDoc4:
HyperDoc4:
HyperDoc4 HyperDocs Padlet
HyperDoc: Образцы HyperDocs
HyperDoc: Как HyperDocs могут преобразовать ваше обучение
HyperDocs для учителей **
HyperDoc: Google+ HyperDocs
HyperDoc 9000 9000 HyperDoc 9000 9000 9000 9000 HyperDoc 9000 9000 9000 9000 9000 9000 Когда тебе нет ut Of Classroom
HyperDoc Lessons — GOOD
HyperDoc: Hyperdoc Lesson Template — хорошо!
HyperDoc: Изучение HyperDocs
HyperDoc: Let’s Rock With HyperDocs — Сотрудничество — видео
Библиотека HyperDoc
HyperDocs: Padlet of HyperDocs — Хорошо!
HyperDoc: Hyper Docs PD Gameboard
HyperDocs: OnAir видео
HyperDoc3 000
HyperDocs: Обучение, ориентированное на студентов, и 4 CS — Сообщество Google Keep — множество ссылок
HyperDoc: Совместное использование HyperDoc
Что вы знаете HyperDoc HyperDoc
HyperDoc: Использование HyperDoc в нашем классе
HyperDoc: Использование HyperDocs в классе
000 HyperDoc
в HyperDoc
HyperDoc: U se Graphic Organizer на HyperDocs для сбора мыслей
HyperDocs Virtual Summit
HyperDoc: Что такое HYPE в HyperDocs?
HyperDoc: Что такое HyperDoc?
HyperDoc: Что такое гипертекстовые документы?
HyperDoc: Почему студентам нравятся HyperDocs
HyperDocs: YouTube HyperDocs
Measurement in Science (Stanford Encyclopedia 9000 Philosophy)
Современные философские дискуссии об измерении — начиная с конец девятнадцатого века до наших дней — можно разделить в несколько направлений науки.Эти пряди отражают разные взгляды на характер измерения и условия, которые делают измерение возможно и надежно. Основные нити математические теории измерения, операционализм, конвенционализм, реализм, теоретико-информационные счета и счета на основе моделей. Эти пряди стипендии, по большей части, не составляют непосредственно конкурирующие взгляды. Вместо этого их лучше всего понимать как выделение различные и дополнительные аспекты измерения. Ниже приводится очень приблизительный обзор этих перспектив:
- Математические теории измерение рассматривать измерение как отображение качественного эмпирические отношения к отношениям между числами (или другими математическими сущностей).
- Операционалисты и традиционалисты просмотр измерение как набор операций, формирующих смысл и / или регулировать использование количественного термина.
- Реалисты рассматривают измерение как оценку независимые от разума свойства и / или отношения.
- Теоретико-информационные счета Просмотр измерений как сбор и интерпретация информации о система.
- Счета на основе моделей рассматривают измерения как согласованное присвоение значений параметрам в теоретической и / или статистическая модель процесса.
Эти точки зрения в принципе согласуются друг с другом. Пока математические теории измерения имеют дело с математическими основы шкал измерения, операционализм и конвенционализм в первую очередь связаны с семантикой количественных терминов, реализмом занимается метафизическим статусом измеримых величин, теоретико-информационные и модельные счета связаны с эпистемологические аспекты измерения. Тем не менее, предмет домен разделен не так аккуратно, как предполагает приведенный выше список.вопросы по метафизике, эпистемологии, семантике и математике основы измерения взаимосвязаны и часто опираются на одну еще один. Следовательно, например, операционалисты и конвенционалисты часто придерживался антиреалистических взглядов, а сторонники модельного счета выступили против преобладающей эмпирической интерпретации математических теорий измерения. Эти тонкости станут ясно из следующего обсуждения.
Список направлений стипендии не является исключительным и исчерпывающий.Он отражает историческую траекторию философского обсуждение до сих пор, а не какое-либо принципиальное различие между разные уровни анализа измерений. Некоторые философские работы по замерам относятся к более чем одной нити, в то время как многие другие работы тоже не подходят прямо. Это особенно актуально, поскольку начале 2000-х, когда измерение вернулось на первый план философская дискуссия после нескольких десятилетий относительного пренебрежения. Эту недавнюю стипендию иногда называют « эпистемология измерения »и включает в себя богатый набор работ которые еще нельзя разделить на отдельные школы мысли.В последний раздел этой записи будет посвящен обзору некоторых из эти события.
Хотя философия измерения сформировалась как отдельная область исследование только во второй половине девятнадцатого века, фундаментальные концепции измерения, такие как величина и количество обсуждаются с древних времен. Согласно Евклиду Элементы , величина, например линия, поверхность или твердый — измеряет другое, когда последнее является целым кратным первое (Книга V, опр.1 и 2). Две величины имеют общую измерять, когда они оба целые кратные некоторой величины и несоизмеримые в противном случае (Книга X, определение 1). Открытие несоизмеримые величины позволили Евклиду и его современникам развивать понятие отношения величин. Соотношения могут быть либо рациональным, либо иррациональным, поэтому понятие соотношения более общий, чем мера (Michell 2003, 2004a; Grattan-Guinness 1996).
Аристотель различал количество и качество.Примеры количества — это числа, линии, поверхности, тела, время и место, а примерами качеств являются справедливость, здоровье, горячность и бледность ( Категории §6 и §8). В соответствии с Аристотеля, количества допускают равенство и неравенство, но не допускают градусов, так как «одна вещь не более четырех футов, чем другая» (Там же 6.6a19). Качества, наоборот, не допускают равенства или неравенство, но допускают степени, «потому что одно называется более бледный или менее бледный, чем другой »(там же 8.10b26).Аристотель не уточняет, являются ли степени таких качеств, как бледность соответствуют различным качествам или одинаковому качеству, бледность, была способна к разной интенсивности. Эта тема была на центр продолжающихся дебатов в тринадцатом и четырнадцатом веках (Юнг 2011). Дунс Скот поддержал «теорию сложения», в соответствии с которым изменение степени качества может быть объясняется сложением или вычитанием меньших степеней этого качество (2011: 553). Позже эта теория была уточнена Николь Орем, которые использовали геометрические фигуры для представления изменений интенсивности такие качества, как скорость (Clagett 1968; Sylla 1971).Oresme’s геометрические представления установили подмножество качеств, которые поддаются количественной обработке, что ставит под сомнение строгая аристотелевская дихотомия между количеством и качеством. Эти разработки позволили сформулировать количественные законы движение в течение шестнадцатого и семнадцатого веков (Грант 1996).
Концепция качественной интенсивности была развита Лейбницем. и Канта. «Принцип непрерывности» Лейбница заявил что все естественные изменения происходят постепенно.Лейбниц утверждал, что этот принцип применим не только к изменениям в расширенных величинах, таких как длины и продолжительности, но также и интенсивности репрезентативных состояния сознания, такие как звуки (Jorgensen 2009; Diehl 2012). Считается, что Кант опирался на принцип Лейбница непрерывность, чтобы сформулировать различие между экстенсивным и интенсивные величины. Согласно Канту, экстенсивные величины те, «в которых представление частей делает возможным представление целого »(1787: A162 / B203).Пример это длина: линию можно мысленно представить только последовательными синтез, в котором части линии соединяются, образуя целое. Для Канта возможность такого синтеза была обоснована в формах интуиция, а именно пространство и время. Интенсивные величины, такие как тепло или цвета, также бывают в непрерывной степени, но их восприятие требует место в мгновение ока, а не через последовательный синтез части. Степени интенсивных величин «могут быть только представлен через приближение к отрицанию »(1787: A 168 / B210), то есть воображая их постепенное уменьшение до тех пор, пока полное отсутствие.
Научные достижения девятнадцатого века бросили вызов различие между экстенсивными и интенсивными величинами. Термодинамика и волновая оптика показала, что разница в температуре и оттенке соответствовали различиям в пространственно-временных величинах, таких как скорость и длина волны. Электрические величины, такие как сопротивление и было показано, что проводимость может складываться и делиться, несмотря на не является обширным в кантовском смысле, т.е. не синтезируется из пространственные или временные части.Более того, ранние эксперименты в психофизики предположили, что интенсивности ощущений, такие как яркость и громкость можно представить как сумму «всего заметные различия »между стимулами, и поэтому мыслится как состоящие из частей (см. Раздел 3.3). Эти результаты, наряду с достижениями в аксиоматизации ветвей математики, мотивировала некоторых из ведущих ученых конца девятнадцатого века, чтобы попытаться прояснить математические основы измерения (Максвелл 1873; фон Крис 1882; Гельмгольц 1887; Мах 1896; Пуанкаре 1898; Hölder 1901; для исторических обзоров см. Darrigol 2003; Michell 1993, 2003; Канту и Шлаудт 2013; Бьяджоли 2016: гл.4, 2018). Эти работы сегодня рассматриваются как предшественники научной стипендии, известной как «измерение теория ».
Математические теории измерения (часто называемые вместе как «теория измерения») относятся к условиям при какие отношения между числами (и другими математическими объектами) могут быть используется для выражения отношений между объекты. [2] Чтобы понять необходимость математических теорий измерения, учтите тот факт, что отношения, выставленные числа, такие как равенство, сумма, разница и соотношение, не всегда соответствуют отношениям между объектами, измеряемыми этими числа.Например, 60 — это дважды 30, но можно ошибиться в думая, что объект, измеренный при 60 градусах Цельсия, в два раза горячее как объект при 30 градусах Цельсия. Это потому, что нулевая точка шкала Цельсия произвольна и не соответствует отсутствию из температура. [3] Точно так же числовые интервалы не всегда содержат эмпирические данные. Информация. Когда испытуемых просят оценить по шкале от 1 до 7 насколько сильно они согласны с данным утверждением, нет прима facie причина полагать, что интервалы между 5 и 6 и от 6 до 7 соответствует равному приросту силы мнения.В качестве третьего примера, равенство чисел транзитивно [если (a = b & b = c), затем a = c], но эмпирические сравнения физических величины обнаруживают только примерное равенство, которое не является переходным связь. Эти примеры показывают, что не все математические отношения между числами, используемыми в измерениях, эмпирически значительный, и что различные виды шкалы измерения передают различные виды эмпирически значимой информации.
Изучение шкал измерений и эмпирической информации в них Передача — это основная задача математических теорий измерения.В его основополагающее эссе 1887 года «Подсчет и измерение», Германн фон Гельмгольц сформулировал ключевой вопрос теории измерений как следует:
[W] Это объективный смысл выражения через деноминацию нумерует отношения реальных объектов как величины, а под каким условия мы можем это сделать? (1887: 4)
Вообще говоря, теория измерений направлена на (i) определение предположения, лежащие в основе использования различных математических структур для описывать аспекты эмпирического мира и (ii) извлекать уроки из адекватность и пределы использования этих математических структур для описание аспектов эмпирического мира.По следам Отто Гёльдера (1901), теоретики измерения часто достигают этих целей через формальные доказательства, с предположениями в (i), служащими аксиомами и уроками в (ii) следующее как теоремы. Ключевое понимание теории измерений: что эмпирически значимые аспекты данной математической структура — это те, которые отражают соответствующие отношения среди объекты измерения. Например, отношение «больше чем »среди чисел является эмпирически значимым для измерения длина, поскольку она отражает отношение «длиннее, чем» среди объектов.Это отражение или отображение отношений между объекты и математические объекты составляют шкалу измерения. В качестве будет пояснено ниже, шкалы измерений обычно понимаются как изоморфизмы или гомоморфизмы между объектами и математическими сущности.
Помимо этих общих целей и заявлений, теория измерений — это весьма неоднородный корпус ученых. В него входят произведения, охватывающие с конца девятнадцатого века до наших дней и поддерживают широкую множество взглядов на онтологию, эпистемологию и семантику измерение.Два основных различия между математическими теориями Особого упоминания заслуживают измерения. Первый касается природа relata , или «объектов», чьи числа отношений должны быть зеркальными. Эти relata могут быть понимается как минимум четырьмя способами: как конкретный человек объекты, как качественные наблюдения за конкретными отдельными объектами, как абстрактные представления отдельных объектов или как универсальные свойства объектов. Какая интерпретация будет принята, зависит от большая часть авторского метафизического и эпистемологического обязательства.Этот вопрос будет особенно актуален для обсуждения. реалистичных счетов измерения (Раздел 5). Во-вторых, разные теоретики измерения занимают разные позиции. на вид эмпирических данных, необходимых для установления сопоставления между объектами и числами. В результате измерения теоретики расходятся во мнениях относительно необходимых условий для установление измеримости атрибутов, и особенно измеримы ли психологические атрибуты. Споры о измеримость оказались очень плодотворными для развития теории измерений, и в следующих подразделах будут представлены некоторые этих дебатов и разработанных в них центральных концепций.
3.1 Фундаментальные и производные измерения
В конце девятнадцатого и начале двадцатого веков несколько Были предприняты попытки дать универсальное определение измерения. Хотя способы измерения различались, единодушное мнение заключалось в том, что измерение — это метод присвоения номеров величин . Например, Гельмгольц (1887: 17) определил измерение как процедуру по которому можно найти номинальное число, которое выражает значение величина, где «номинальное число» — это число вместе с агрегатом, эл.г., 5 метров, а величина — качество объекты, которые можно упорядочить от меньшего к большему, например, длина. Бертран Рассел так же заявил, что измерение равно
.любой метод, с помощью которого осуществляется уникальное взаимное соответствие установленное между всеми или некоторыми величинами вида и всеми или некоторые числа, целые, рациональные или действительные. (1903: 176)
Норман Кэмпбелл определил измерение просто как «процесс присвоение чисел для представления качеств », где качество — это свойство, допускающее непроизвольное упорядочение (1920: 267).
Определение измерения как числового присвоения поднимает вопрос: какие задания подходят и при каких условиях? Рано теоретики измерения, такие как Гельмгольц (1887 г.), Гельдер (1901 г.) и Кэмпбелл (1920) утверждал, что числа подходят для выражения величины, поскольку алгебраические операции между числами отражают эмпирические отношения между величинами. Например, качественный отношение «длиннее чем» среди жестких стержней (примерно) переходные и асимметричные, и в этом отношении разделяет структурные функции с отношением «больше чем» среди чисел.Кроме того, сквозное соединение жестких стержней разделяет конструктивные функции, такие как ассоциативность и коммутативность, с математическая операция сложения. Аналогичная ситуация имеет место для измерение веса с помощью равноправных весов. Здесь отклонение оружие обеспечивает упорядочивание между гирями и нагромождение гирь на одна сковорода представляет собой соединение.
Ранние теоретики измерения сформулировали аксиомы, описывающие эти качественных эмпирических структур и использовал эти аксиомы для доказательства теоремы об адекватности приписывания чисел величинам, которые выставлять такие конструкции.В частности, они доказали, что заказывая и конкатенации вместе достаточны для построения аддитивное числовое представление соответствующих величин. Аддитивное представление — это такое представление, в котором сложение эмпирически осмысленный, а значит, и умножение, деление и т. д. Кэмпбелл так называемые процедуры измерения, удовлетворяющие условиям аддитивность «фундаментальная», потому что они не включают измерение любой другой величины (1920: 277). Виды величин для которого была применена фундаментальная процедура измерения найдено — например, длина, площадь, объем, продолжительность, вес и электрическое сопротивление — Кэмпбелл назвал «фундаментальным величины ».Отличительной чертой таких масштабов является то, что это их можно сгенерировать, объединив стандартную последовательность равные единицы, как в примере серии равномерных знаков на линейка.
Хотя они считали аддитивность отличительной чертой измерения, большинство ранние теоретики измерения признали, что аддитивность не необходимо для измерения. Существуют и другие величины, допускающие упорядочение. от меньшего к большему, но чьи соотношения и / или различия не могут в настоящее время быть определенными, кроме как через их отношения с другими, фундаментально измеримые величины.Примеры: температура, которая может быть измерен путем определения объема ртутного столба, и плотность, которая может быть измерена как отношение массы к объему. Такой косвенное определение стало называться «производным» измерения и соответствующие величины «получены величины »(Кэмпбелл 1920: 275–77).
На первый взгляд, различие между фундаментальным и производным измерение может показаться напоминанием о различии между обширными и интенсивные величины, и действительно фундаментальное измерение иногда называют «обширным».Тем не менее, важно отметить, что эти два различия основаны на существенно разных критерии измеримости. Как обсуждалось в Раздел 2, экстенсивно-интенсивное различие сосредоточено на собственном структура рассматриваемой величины, т. е. является ли она состоит из пространственно-временных частей. Основополагающий различие, напротив, фокусируется на свойствах измерения операций . Принципиально измеримая величина — это величина в котором была найдена фундаментальная операция измерения.Следовательно, фундаментальность не является внутренним свойством величина: полученная величина может стать фундаментальной с открытие новых операций по его измерению. Более того, в фундаментальное измерение числовое присвоение не обязательно отражает структура пространственно-временной части. Электрическое сопротивление, для Например, можно принципиально измерить, подключив резисторы в серия (Кэмпбелл 1920: 293). Это считается фундаментальным операция измерения, потому что она имеет общую структуру с числовыми кроме того, даже если объекты с одинаковым сопротивлением обычно не равные по размеру.
Различие между фундаментальным и производным измерением было переработано последующими авторами. Брайан Эллис (1966: гл. 5–8) различают три типа измерения: фундаментальный, ассоциативное и производное. Фундаментальные измерения требуют заказа и операции конкатенации, удовлетворяющие тем же условиям, указанным в Кэмпбелл. Процедуры ассоциативных измерений основаны на корреляция двух отношений упорядочения, например, корреляция между объемом ртутного столба и его температурой.Полученный Процедуры измерения заключаются в определении значения константа в физическом законе. Константа может быть локальной, как в определение удельной плотности воды по массе и объему, или универсальный, как в определении ньютоновского гравитационного постоянная от силы, массы и расстояния. Генри Кибург (1984: гл. 5–7) предложил несколько иное тройное различие между прямое, косвенное и систематическое измерение, которое не полностью перекрывается с Эллис. [4] Более радикальный пересмотр различия между фундаментальным и производное измерение было предложено Р. Дунканом Люсом и Джоном Тьюки. (1964) в своей работе по совместному измерению, которая будет обсуждаться в Раздел 3.4.
3.2 Классификация весов
В предыдущем подразделе обсуждалась аксиоматизация эмпирических структуры, линия расследования, которая восходит к ранним дням теория измерений. Дополнительная информация в рамках измерения Теория касается классификации шкал измерений.В психофизик С.С.Стивенс (1946, 1951) выделил четыре виды шкал: именные, порядковые, интервальные и кратные. Номинальные шкалы представлять объекты как принадлежащие к классам, которые не имеют порядок, например, мужской и женский. Порядковые шкалы представляют порядок, но не дальнейшая алгебраическая структура. Например, минеральная шкала Мооса твердость представляет собой минералы с номерами от 1 (самый мягкий) до 10 (самый сложный), но нет никакого эмпирического значения равенства между интервалы или соотношения тех числа. [5] Цельсия и Фаренгейта являются примерами интервальных шкал: они представляют равенство или неравенство между интервалами температуры, но не отношения температур, потому что их нулевые точки произвольны. Шкала Кельвина, напротив, представляет собой шкалу отношений, как и знакомые шкалы, отображающие массу в килограммах, длину в метрах и продолжительность в секундах. Позже Стивенс уточнил эту классификацию и различают линейные и логарифмические интервальные шкалы (1959: 31–34) и между шкалами отношений с натуральной единицей и без нее. (1959: 34).Шкалы коэффициентов с натуральными единицами измерения, например, используемые для подсчета дискретных объектов и представления вероятностей, были названы «абсолютными» шкалами.
Как отмечает Стивенс, типы шкал индивидуализированы по семействам трансформации, которые они могут претерпеть без потери эмпирических Информация. Эмпирические зависимости, представленные на шкалах отношений, для например, инвариантны относительно умножения на положительное число, например, умножение на 2,54 преобразует дюймы в сантиметры. Линейные интервальные шкалы допускают как умножение на положительное число и постоянный сдвиг, e.г., преобразование из Цельсия в Фаренгейт в соответствии с формулой ° C × 9/5 + 32 = ° F. Порядковые шкалы допускают любую функцию преобразования, пока она монотонно-возрастающие, а номинальные шкалы допускают взаимно однозначные подмена. Абсолютные шкалы не допускают никаких преобразований, кроме личность. Классификация весов Стивенса была позже обобщены Луи Наренсом (1981, 1985: гл. 2) и Люс и др. (1990: Гл. 20) с точки зрения однородности и уникальности соответствующих группы трансформации.
В то время как классификация шкал Стивенса встретила общие одобрение в научных и философских кругах, его шире значение для теории измерений стало темой значительных дебаты. Особо оспаривались два вопроса. Во-первых, было ли операции классификации и упорядочивания заслуживают того, чтобы называться «Измерительные» операции и, соответственно, представление величин на номинальной и порядковой шкалах должно считать как измерение. Несколько физиков, в том числе Кэмпбелл, утверждали, что что операции классификации и упорядочивания не обеспечили достаточно богатая структура, чтобы гарантировать использование чисел, и, следовательно, не должны считаться измерительными операциями.Второй оспариваемый вопрос нужно ли было найти операцию конкатенации для величины до того, как его можно было фундаментально измерить по шкале отношений. Дебаты стал особенно горячим, когда снова разгорелся более длительный спор окружающая измеримость интенсивности ощущений. Это чтобы мы переходим к этой дискуссии.
3.3 Измеримость ощущений
Один из главных катализаторов развития математических теорий измерения были продолжающимися дебатами об измеримости в психология.Эти дебаты часто восходят к работе Густава Фехнера. (1860) Elements of Psychophysics , в котором он описал метод измерения интенсивности ощущений. Метод Фехнера был основан на записи «едва заметных различия »между ощущениями, связанными с парами стимулы, например, два звука разной интенсивности. Эти различия были приняты равные приращения интенсивности ощущения. В качестве Фехнер показал, что при этом предположении стабильная линейная зависимость между интенсивностью ощущений и логарифмом интенсивность стимула, отношение, которое стало известно как «Закон Фехнера» (Heidelberger 1993a: 203; Luce and Suppes 2004: 11–2).Этот закон, в свою очередь, обеспечивает метод косвенное измерение интенсивности ощущений путем измерения интенсивность стимула и, следовательно, утверждал Фехнер, обеспечивает обоснование измерения интенсивности ощущений на реальном числа.
Утверждения Фехнера об измеримости ощущений стал предметом серии дебатов, которые длились почти столетие и оказался чрезвычайно полезным для философии измерения, с участием таких ключевых фигур, как Мах, Гельмгольц, Кэмпбелл и Стивенс (Heidelberger 1993a: Ch.6 и 1993b; Мичелл 1999: гл. 6). Те возражая против измеримости ощущений, например, Кэмпбелл, подчеркнул необходимость эмпирической операции конкатенации для фундаментальное измерение. Поскольку интенсивности ощущений не могут быть соединены друг с другом в соответствии с длинами и веса, фундаментального измерения ощущений быть не может. интенсивность. Более того, Кэмпбелл утверждал, что ни одно из психофизических обнаруженные к настоящему времени закономерности достаточно универсальны, чтобы как законы в том смысле, который требуется для производных измерений (Кэмпбелл в Ferguson et al.1940: 347). Все, что показали психофизики, что интенсивности ощущений можно последовательно упорядочить, но порядок сам по себе еще не гарантирует использование числовых соотношений, таких как суммы и соотношения для выражения эмпирических результатов.
Центральным противником Кэмпбелла в этой дискуссии был Стивенс, чей Различие между типами шкалы измерений обсуждалось выше. Стивенс определил измерение как «присвоение цифр объекты или события в соответствии с правилами »(1951: 1) и утверждал, что любое последовательное и неслучайное распределение считается измерением в в широком смысле (1975: 47).В полезных случаях научного исследования Стивенс заявлено, измерение может быть истолковано несколько более узко как числовое присвоение, основанное на результатах сопоставления операции, такие как связь температуры с объемом ртути или соответствие ощущений друг другу. Стивенс выступал против считают, что отношения между числами должны отражать качественные эмпирические структур, утверждая вместо этого, что шкалы измерений должны быть рассматриваются как произвольные формальные схемы и принимаются в соответствии с их полезность для описания эмпирических данных.Например, приняв шкала соотношения для измерения ощущений громкости, громкости и плотность звуков приводит к формулировке простой линейной зависимости среди отчетов подопытных: громкость = громкость × плотность (1975: 57–8). Такое присвоение чисел ощущениям считается измерением, потому что оно непротиворечиво и неслучайно, потому что он основан на операциях согласования, выполняемых экспериментальными субъектов, и поскольку он фиксирует закономерности в экспериментальных полученные результаты. По словам Стивенса, эти условия совпадают. достаточно, чтобы оправдать использование шкалы отношений для измерения ощущения, несмотря на то, что «ощущения не могут быть разделены на составные части или уложены встык, как измерения палки »(1975: 38; см. также Hempel 1952: 68–9).
3.4 Репрезентативная теория измерения
В середине двадцатого века два основных направления исследований в теория измерения, посвященная эмпирическим условиям количественная оценка и классификация шкал, сошлись в работах Патрика Суппеса (1951; Скотт и Суппс 1958; для исторических обзоров см. Savage and Ehrlich 1992; Diez 1997a, b). Работа Суппеса заложила основу репрезентативной теории Измерение (RTM), которое остается наиболее влиятельным математическим теория измерений на сегодняшний день (Krantz et al.1971; Suppes et al. 1989; Luce et al. 1990). RTM определяет измерение как построение отображения из эмпирических реляционных структур в числовые реляционные структуры (Krantz et al. 1971: 9). Эмпирический реляционный конструкция состоит из набора эмпирических объектов (например, жестких стержней) наряду с определенными качественными отношениями между ними (например, упорядочивание, конкатенация), а числовая реляционная структура состоит из набор чисел (например, действительные числа) и конкретные математические отношения между ними (e.g., «равно или больше», добавление). Проще говоря, шкала измерения — это соотношение «многие к одному». отображение — гомоморфизм — от эмпирического к числовому реляционная структура, а измерение — это построение напольные весы. [6] RTM очень подробно разъясняет предположения, лежащие в основе построение различных типов измерительных шкал. Каждый тип масштаба связана с набором предположений о качественном отношения, возникающие между объектами, представленными на этом типе шкалы.Из этих предположений или аксиом авторы RTM выводят репрезентативная адекватность каждого типа шкалы, а также семейства допустимые преобразования, делающие этот тип шкалы уникальным. В этом способ RTM обеспечивает концептуальную связь между эмпирической основой измерение и типология напольные весы. [7]
Что касается измеримости, Репрезентативная теория принимает средний путь между либеральным подходом Стивенса и Строгий упор на операции конкатенации, поддерживаемый Кэмпбеллом.Нравиться Кэмпбелл, RTM признает, что правила количественной оценки должны быть основаны на известные эмпирические структуры и не должны выбираться произвольно, чтобы соответствовать данные. Однако RTM отвергает идею о том, что аддитивные шкалы адекватно только тогда, когда доступны операции конкатенации (Люс и Суппес 2004: 15). Вместо этого RTM отстаивает существование фундаментальных операции измерения, не связанные с конкатенацией. Центральный пример этого типа операции известен как «аддитивное соединение измерения »(Люс и Тьюки 1964; Кранц и др.1971: 17–21 и гл. 6–7). Здесь измерения двух или более различные типы атрибутов, такие как температура и давление газа, получаются путем наблюдения за их совместным действием, таким как объем газа. Люси и Тьюки показали это, установив определенные качественные отношения между объемами при изменении температуры и давления, можно построить аддитивные представления температуры и давления, без использования каких-либо предшествующих методов объем измерения. Подобная процедура может быть обобщена на любой соответствующим образом связанный триплет атрибутов, таких как громкость, интенсивность и частота чистых тонов или предпочтение награды, размер и задержка в получении (Luce and Suppes 2004: 17).В открытие аддитивного совместного измерения привело авторов RTM к разделить фундаментальные измерения на два вида: традиционные измерения процедуры, основанные на операциях конкатенации, которые они назвали «Обширное измерение» и совместное или «Неэкстенсивное» фундаментальное измерение. Под этим новым концепция фундаментальности, все традиционные физические атрибуты можно измерить фундаментально, как и многие психологические атрибуты (Krantz et al. 1971: 502–3).
Выше мы видели, что математические теории измерения в первую очередь связаны с математическими свойствами измерительных шкал и условия их применения.Родственная, но отличная нить стипендия касается значения и использования количественных терминов. Научный теории и модели обычно выражаются в терминах количественных отношения между параметрами, имеющими имена, такие как «Продолжительность», «уровень безработицы» и «Интроверсия». Реалист об одном из этих терминов утверждают, что это относится к набору свойств или отношений, которые существуют независимо от измерения. Операционалист или традиционалист будет утверждать, что способ применения таких количественных терминов к бетону детали зависят от нетривиального выбора, сделанного людьми, и конкретно о вариантах выбора, связанных с тем, как количество измеряется.Обратите внимание, что в рамках этой широкой концепции реализм совместим с операционализмом и конвенционализмом. То есть это возможно, что выбор метода измерения регулирует использование количество-член и что, если правильный выбор , этот термин преуспевает в ссылке на независимое от разума свойство или отношение. Тем не менее многие операционалисты и конвенционалисты приняли более сильные взгляды, согласно которым нет фактов, поскольку какая из нескольких и нетривиально разных операций верна для применения данного количественного термина.Эти более сильные варианты несовместимо с реализмом об измерениях. Этот раздел будет посвященный операционализму и конвенционализму, а следующий реализм об измерении.
Операционализм (или «операционизм») в отношении измерения — это точка зрения, что значение количественных понятий определяется набор операций, используемых для их измерения. Самое сильное выражение операционализма появляется в ранних работах Перси Бриджмена (1927), кто утверждал, что
мы подразумеваем под любым понятием не более чем набор операций; в понятие является синонимом соответствующего набора операций.(1927: 5)
Например, длина будет определяться как результат операции сцепления жестких стержней. Согласно этой крайней версии операционализм, разные операции измеряют разные величины. Длина измеряется линейками и синхронизацией электромагнитных импульсов следует, строго говоря, различать два различных количественные понятия, помеченные как «длина-1» и «Длина-2» соответственно. Этот вывод привел Бриджмена к утверждают, что принятые в настоящее время количественные концепции «Суставы», где различные операции перекрываются в своих область применения.Он предостерег от догматической веры в единство количественных концепций в этих «суставах», вместо этого это единство проверяется экспериментами всякий раз, когда применение количественное понятие должно быть расширено в новую область. Тем не менее, Бриджмен признал, что до тех пор, пока результаты различных операций согласен в пределах экспериментальной ошибки, прагматически оправдано маркировать соответствующие величины с таким же названием (1927: 16). [8]
Операционализм стал влиятельным в психологии, где он был хорошо принят такими бихевиористами, как Эдвин Боринг (1945) и Б.Ф. Скиннер (1945). В самом деле, Скиннер утверждал, что бихевиоризм «Не более чем тщательный оперативный анализ традиционные менталистские концепции »(1945: 271). Стивенс, который был Ученик Скуки был одним из главных пропагандистов операционализма в психологии и утверждал, что психологические концепции имеют эмпирические имея в виду, только если они означают определенные и конкретные операции (1935: 517; см. также Isaac 2017). Идея о том, что концепции определяются операции измерения согласуются с либеральными взглядами Стивенса по измеримости, которые обсуждались выше (Раздел 3.3). Поскольку присвоение номеров объектам выполняется в в соответствии с конкретными и последовательными правилами, Стивенс утверждал, что такое задание имеет эмпирическое значение и не должно удовлетворять никаким дополнительные ограничения. Тем не менее, Стивенс, вероятно, не принял антиреалистический взгляд на психологические атрибуты. Вместо этого там веские причины думать, что он понимал операционализм как методологический подход, который был ценен в той мере, в какой он позволили психологам обосновать выводы, которые они сделали из эксперименты (Feest 2005).Например, Стивенс не лечил рабочие определения как априори , но как поддающиеся улучшение в свете эмпирических открытий, подразумевая, что он взял психологические атрибуты существуют независимо от таких определений (Стивенс 1935: 527). Это говорит о том, что операционализм Стивенса было более умеренным разнообразием, чем то, что было в ранних писаниях из Бриджмен. [9]
Операционализм с первоначальным энтузиазмом встретил логические позитивисты, которые рассматривал это как сродни верификации.Тем не менее, это было скоро показали, что любая попытка основать теорию значения на операционалистские принципы были полны проблем. Среди таких проблемы были автоматическим операционализмом надежности измерения, двусмысленность, окружающая понятие эксплуатации, чрезмерно ограничительный рабочий критерий осмысленность и тот факт, что многие полезные теоретические концепции не хватает четких операционных определений (Чанг 2009 г.). [10] В частности, Карл Хемпель (1956, 1966) критиковал операционалистов. за неспособность дать определение диспозиционных терминов, таких как «Растворимость в воде», а также для умножения количества научные концепции в манере, которая противоречит необходимости систематические и простые теории.Соответственно, большинство авторов семантика количественных терминов избегает поддержки операционного анализ. [11]
Более широко распространенный подход допускал традиционный элемент в использование количественных терминов, сопротивляясь попыткам уменьшить значение количественных терминов для операций измерения. Эти аккаунты относятся к общей рубрике «Конвенционализм», хотя они отличаются аспекты измерения, которые они считают общепринятыми, и в степени произвол они приписывают таким условности. [12] Первым предшественником конвенционализма был Эрнст Мах, исследовавший понятие равенства температурных интервалов (1896: 52). Мах отметил, что разные типы термометрической жидкости расширяются при разных (и нелинейно связанные) скорости при нагревании, в связи с чем возникает вопрос: какая жидкость расширяется наиболее равномерно с температурой? В соответствии с Мах, не важно, какая жидкость расширяется больше. равномерно, поскольку само понятие равенства температур интервалы не имеют определенного применения до обычного выбор стандартной термометрической жидкости.Мах придумал термин «Принцип согласованности» для такого рода условно выбранный принцип применения количества концепция. Понятия единообразия времени и пространства получили аналогичные обработки Анри Пуанкаре (1898, 1902: Часть 2). Пуанкаре утверждал, что процедуры, используемые для определения равенства среди длительностей проистекает из неосознанного предпочтения ученых описательная простота, а не из каких-либо фактов о природе. Точно так же выбор ученых представить пространство либо Евклидова или неевклидова геометрия не определяется опытом но из соображений удобства.
Конвенционализм в отношении измерения достиг своего максимума. сложное выражение в логическом позитивизме. Логические позитивисты как Ганс Райхенбах и Рудольф Карнап предложили «координационный определения »или« правила соответствия »как семантическая связь между теоретическими и наблюдательными терминами. Эти a priori , утверждения, подобные определениям, предназначались для регулирования использование теоретических терминов, связав их с эмпирическими процедурами (Reichenbach 1927: 14–19; Carnap 1966: Ch.24). Пример Координационным определением является утверждение: «мерный стержень сохраняет свою длину при транспортировке ». По словам Райхенбаха, это утверждение не может быть проверено эмпирически, потому что универсальный и могла существовать экспериментально необнаруживаемая сила, которая в равной степени искажает длина каждого объекта при транспортировке. В соответствии с верификационизм, утверждения, которые невозможно проверить, не являются ни правдой, ни ложный. Вместо этого Райхенбах воспринял это заявление как выражение произвольное правило, регулирующее использование понятия равенства length, а именно для определения того, являются ли конкретные экземпляры length равны (Reichenbach 1927: 16).В то же время координационные определения не рассматривались как замена, а скорее как необходимые дополнения к знакомому типу теоретических определений понятий с точки зрения других концепций (1927: 14). Под условным точки зрения, то спецификация измерительных операций не исчерпывают значение таких понятий, как длина или равенство длины, тем самым избегая многих проблем, связанных с операционализм. [13]
Реалисты в области измерения утверждают, что измерение лучше понимается как эмпирическая оценка объективного свойства или связь.Сделаем несколько пояснительных замечаний в отношении это характеристика измерения. Во-первых, термин «Объективный» не предназначен для исключения ментальных свойств или отношения, которые являются объектами психологического измерения. Скорее, измеримые свойства или отношения считаются объективными, поскольку поскольку они не зависят от верований и условностей людей выполнение измерения и методы, используемые для измерения. За Например, реалист будет утверждать, что отношение длины данного сплошная штанга к стандартному счетчику имеет объективное значение независимо от измеряется ли и как.Во-вторых, срок «Оценка» используется реалистами, чтобы подчеркнуть факт что результаты измерений являются всего лишь приближениями истинных ценности (Trout 1998: 46). В-третьих, по мнению реалистов, измерение направленных на получение знаний о свойствах и отношениях, скорее чем при присвоении значений непосредственно отдельным объектам. Это значимы, потому что наблюдаемые объекты (например, рычаги, химические решения, люди) часто определяют измеримые свойства и отношения, которые не наблюдаются напрямую (например,г., количество механических работа, кислая, интеллект). Заявления о знаниях о таких свойства и отношения должны предполагать некоторую базовую теорию. К перенос акцента с объектов на свойства и отношения, реалисты подчеркивают теоретический характер измерений.
Реализм в отношении измерения не следует путать с реализмом в отношении сущности (например, электроны). Реализм в измерениях обязательно влечет за собой реализм в отношении свойств (например, температуры), поскольку в принципе можно было принять только реальность отношений (напр.грамм., соотношений между количествами), не принимая во внимание реальность лежащих в основе характеристики. Тем не менее, большинство философов, защищавших реализм об измерении сделали это, отстаивая реализм в той или иной форме о свойствах (Байерли и Лазара 1973; Свойер 1987; Манди 1987; Форель 1998, 2000). Эти реалисты утверждают, что по крайней мере некоторые измеримые свойства существуют независимо от убеждений и условностей люди, которые их измеряют, и что существование и структура этих properties наилучшим образом объясняет ключевые особенности измерение, включая полезность чисел при выражении результаты измерений и надежность средств измерений.
Например, типичный реалист по поводу измерения длины поспорит что эмпирические закономерности, отображаемые отдельными объектами » длины, когда они упорядочены и объединены, лучше всего объясняются предполагая, что длина является объективным свойством, имеющим обширную структура (Swoyer 1987: 271–4). То есть отношения между длинами такие как «дольше чем» и «сумма» существуют независимо от того, были ли какие-либо объекты заказаны и соединены людьми, и действительно независимо от того, являются ли объекты какая-то конкретная длина вообще существует.Существование обширная структура собственности означает, что длины разделяют большую часть их структура с положительными действительными числами, и это объясняет полезность положительных чисел в представлении длин. Более того, если измеримые свойства анализируются с точки зрения диспозиции, становится Легко объяснить, почему некоторые измерительные приборы надежны. За Например, если предположить, что определенное количество электрического тока в проволока влечет за собой склонность отклонять стрелку амперметра определенным угла, следует, что показания амперметра наоборот, зависят от количества электрического тока в проводе, и поэтому амперметр надежен (Trout 1998: 65).
Другой аргумент в пользу реализма в отношении измерения принадлежит Джоэлю. Мичелл (1994, 2005), который предлагает реалистичную теорию чисел, основанную на евклидова концепция соотношения. По словам Мичелла, цифры соотношения между величинами и, следовательно, существуют в пространстве и времени. В частности, действительных чисел — это отношения между парами бесконечные стандартные последовательности, например, последовательность длин обычно обозначается «1 метр», «2 метра» и т. д., а последовательность целых кратных длины, которую мы пытаемся измерить.Измерение — это открытие и оценка таких соотношений. An Интересным следствием этого эмпирического реализма в отношении чисел является это измерение — не репрезентативная деятельность, а скорее деятельность по приближению независимых от разума чисел (Michell 1994: 400).
Реалистические представления об измерениях в основном формулируются противоположно к сильным версиям операционализма и конвенционализма, которые доминировали философские дискуссии об измерениях с 1930-х годов до 1960-х гг.Помимо недостатков операционализма уже обсуждалось в предыдущем разделе, реалисты отмечают, что антиреализм в отношении измеримых величин не может понять научная практика. Если бы количества не имели реальных значений независимо от выбор методики измерения, было бы трудно объясните, что ученые подразумевают под «точностью измерения» и «Ошибка измерения» и почему они пытаются повысить точность и уменьшить ошибку. Напротив, реалисты могут легко понять смысл понятия точности и ошибки с точки зрения расстояния между реальными и измеренные значения (Byerly and Lazara 1973: 17–8; Swoyer 1987: 239; Форель 1998: 57).С этим тесно связан тот факт, что более новые процедуры измерения имеют тенденцию повышать точность по сравнению с более старыми. Если бы выбор процедуры измерения был просто обычным, он бы трудно разобраться в таком прогрессе. Кроме того, реализм дает интуитивно понятное объяснение того, почему разные измерения процедуры часто дают аналогичные результаты, а именно потому, что они чувствительны к тем же фактам (Swoyer 1987: 239; Trout 1998: 56). Наконец, реалисты отмечают, что конструкция измерительной аппаратуры и при анализе результатов измерений руководствуемся теоретическими предположения относительно причинно-следственных связей между величинами.В способность таких причинно-следственных предположений направлять измерения предполагает, что количества онтологически предшествуют процедурам измерения их. [14]
Хотя их отношение к операционализму и конвенционализму в основном критичны, реалисты более снисходительны в своих оценках математические теории измерения. Брент Манди (1987) и Крис Swoyer (1987) оба принимают аксиоматическую трактовку измерения. шкалы, но возражают против эмпирической интерпретации, данной аксиомы выдающихся теоретиков измерений, таких как Кэмпбелл (1920) и Эрнест Нагель (1931; Коэн и Нагель 1934: гл.15). Скорее, чем интерпретация аксиом как относящихся к конкретным объектам или к наблюдаемые отношения между такими объектами, Манди и Свойер переосмысливают аксиомы, относящиеся к универсальным величинам, например, к универсальное свойство быть длиной 5 метров, а не бетоном экземпляры этого свойства. Эта конструкция сохраняет интуиция, что утверждения типа «размер x вдвое размером y ”- это в первую очередь около двух размеров , и только производные об объектах x и и самих себя (Mundy 1987: 34). [15] Манди и Свойер утверждают, что их интерпретация является более общей, потому что это логически влечет за собой все последствия первого порядка эмпирическая интерпретация наряду с дополнительными утверждениями второго порядка о всемирных величинах. Более того, согласно их интерпретации теория измерения становится подлинной научной теорией с объяснительные гипотезы и проверяемые прогнозы. Основываясь на этом работы, Джо Вольф (2020a) недавно предложила новую реалистичную версию величин, которая опирается на репрезентативную теорию Измерение.Согласно структуралистской теории Вольфа количество, количественные атрибуты — это структуры отношений. В частности, атрибут является количественным, если его структура имеет переводы, образующие архимедову упорядоченную группу. Вольфа сосредоточиться на переводах, а не на конкретных отношениях, таких как конкатенация и упорядочение означает, что количественность может быть реализуется множеством способов и не ограничивается обширными конструкции. Это также означает, что быть количеством ничего не значит специально для чисел, как числовых, так и нечисловых структуры могут быть количественными.
Теоретико-информационные отчеты об измерениях основаны на аналогии между измерительными системами и системами связи. В простом система связи, сообщение (вход) кодируется в сигнал на конец передатчика, отправленный на конец приемника, и затем декодируется обратно (вывод). Точность передачи зависит от об особенностях системы связи, а также об особенностях окружающая среда, то есть уровень фонового шума. Аналогичным образом измеряя инструменты можно рассматривать как «информационные машины» (Финкельштейн 1977), которые взаимодействуют с объектом в заданном состоянии (ввод), кодируйте это состояние во внутренний сигнал и преобразуйте это сигнал в считывание (вывод).Точность измерения аналогично зависит от инструмента, а также от уровня шума в его среде. Задуманный как особый вид информации передачи, измерение становится анализируемым с точки зрения концептуальный аппарат теории информации (Hartley 1928; Shannon 1948; Шеннон и Уивер 1949). Например, информация, которая чтение \ (y_i \) сообщает о возникновении состояния \ (x_k \) объект можно количественно оценить как \ (\ log \ left [\ frac {p (x_k \ mid y_i)} {p (x_k)} \ right] \), а именно как функция уменьшения неопределенность в отношении состояния объекта (Finkelstein 1975: 222; для альтернативные формулировки см. Brillouin 1962: Ch.15; Кирпатовский 1974; и Мари 1999: 185).
Людвик Финкельштейн (1975, 1977) и Лука Мари (1999) предложили возможность синтеза теории информации Шеннона-Уивера и теория измерений. По их мнению, обе теории апеллируют к центру. к идее отображения: теория информации касается отображения между символами во входных и выходных сообщениях, при измерении теория касается отображения между объектами и числами. Если измерение аналогично манипулированию символами, тогда Теория Шеннона-Уивера могла бы обеспечить формализацию синтаксиса измерения, в то время как теория измерений могла бы обеспечить формализацию его семантика.Тем не менее Мари (1999: 185) также предупреждает, что аналогия между системами связи и измерения ограничена. В то время как сообщение отправителя может быть известно с произвольной точностью независимо от его передачи состояние объекта не может быть известно с произвольной точностью независимо от его измерения.
Изначально теоретико-информационные отчеты об измерениях были разработаны метрологами — специалистами в области физических измерений и стандартизация — с небольшим участием философов.Независимо от достижений в метрологии, Бас ван Фраассен (2008: 141–185) недавно предложила концепцию измерения в какая информация играет ключевую роль. Он считает измерение составленным двух уровней: на физическом уровне измерительная аппаратура взаимодействует с объектом и производит чтение, например, указатель позиция. [16] На абстрактном уровне фоновая теория представляет собой возможные состояния объекта в пространстве параметров. Измерение находит объект в подобласти этого абстрактного пространства параметров, тем самым сокращая диапазон возможных состояний (2008: 164 и 172).Это сокращение возможностей сводится к сбору информация об измеряемом объекте. Анализ Ван Фраассена измерения отличается от теоретико-информационных счетов, разработанных в метрологии в ее явной апелляции к фоновой теории, а в тот факт, что он не ссылается на символическую концепцию информации разработан Шеннон и Уивер.
С начала 2000-х годов нахлынула новая волна философских исследований. появилось, что подчеркивает взаимосвязь между измерением и теоретическое и статистическое моделирование (Morgan 2001; Boumans 2005a, 2015; Mari 2005b; Мари и Джордани 2013; Таль 2016, 2017; Паркер 2017; Мияке 2017).Согласно расчетам, основанным на модели, измерение состоит из двух уровней: (i) конкретный процесс, включающий взаимодействие между интересующий объект, инструмент и окружение; и (ii) a теоретическая и / или статистическая модель этого процесса, где «Модель» означает абстрактное и локальное представление построены на основе упрощающих предположений. Центральная цель измерение в соответствии с этой точкой зрения заключается в присвоении значений одному или нескольким интересующих параметров модели таким образом, чтобы eptemic desiderata, в частности последовательность и последовательность.
Счета на основе моделей были разработаны путем изучения измерений практики в науке, и особенно в метрологии. Метрология, официально определяется как «наука об измерениях и ее приложение »(JCGM 2012: 2.2), является предметом изучения с разработкой, обслуживанием и усовершенствованием средств измерений в естественных и технических науках. Метрологи обычно работают в бюро стандартизации или в специализированных лабораториях, ответственный за калибровку измерительного оборудования, сравнение стандартов и оценка измерений неопределенности, среди других задач.Только недавно философы начали заниматься богатыми концептуальными проблемами лежащей в основе метрологической практики, и особенно с выводами участвует в оценке и повышении точности измерений стандарты (Chang 2004; Boumans 2005a: Chap. 5, 2005b, 2007a; Frigerio и другие. 2010; Teller 2013, 2018; Риордан 2015; Шлаудт и Хубер 2015; Tal 2016a, 2018; Mitchell et al. 2017; Месснер и Нордманн 2017; de Courtenay et al. 2019).
Основная мотивация для разработки модельных счетов: попытка прояснить эпистемологические принципы, лежащие в основе аспекты измерительной практики.Например, метрологи используют разнообразие методов калибровки средств измерений, стандартизация и отслеживание единиц и оценка неопределенности (обсуждение метрологии см. в предыдущем раздел). Традиционные философские теории, такие как математические теории измерения не основываются на предположениях, выводах шаблоны, доказательства или критерии успеха, связанные с такими методы. Как отмечает Frigerio et al. (2010) утверждают, что теория измерений плохо подходит для разъяснения этих аспектов измерения, поскольку абстрагируется от процесса измерения и фокусируется исключительно на математические свойства весов.Напротив, модельные счета считают построение шкалы лишь одной из нескольких задач участвует в измерении, наряду с определением измеряемого параметры, конструкция и калибровка прибора, отбор образцов и подготовка, обнаружение ошибок и оценка неопределенности, среди прочего (2010: 145–7).
7.1 Роль моделей в измерении
Согласно модельным расчетам, измерение предполагает взаимодействие между интересующим объектом («система под измерение »), инструмент (« измерение система ») и среду, которая включает предметы.Другие, вторичные взаимодействия также могут иметь отношение к определение результата измерения, например, взаимодействие между измерительным прибором и эталонами, используемыми для его калибровка и цепочка сравнений, отслеживающих эталон стандарт обратно к первичным эталонам (Mari 2003: 25). Измерение продолжается путем представления этих взаимодействий с набором параметры и присвоение значений подмножеству этих параметров (известные как «измеряемые величины») на основе результатов взаимодействия.Когда измеряемые параметры являются числовыми, их называют «Количества». Хотя измеряемые величины не обязательно должны быть количествами, будет предложен сценарий количественного измерения, в котором следует.
Два вида результатов измерений различаются по моделям. счета [JCGM 2012: 2.9 и 4.1; Джордани и Мари 2012: 2146; Таль 2013]:
- Показания прибора (или «Чтения»): это свойства измерительного прибор в конечном состоянии после того, как процесс измерения полный.Примеры: цифры на дисплее, отметки при множественном выборе анкета и биты, хранящиеся в памяти устройства. Показания могут быть представлены числами, но такие числа описывают состояния инструмент, и его не следует путать с результатами измерения, которые относятся к состояниям объекта измерения.
- Результаты измерения (или «результаты»): это утверждения о знании значений одной или нескольких величин приписываются измеряемому объекту и обычно сопровождаются указанием единицы измерения и масштаба и сметы неопределенности измерения.Например, результат измерения может быть следующим: выражается предложением «масса объекта a составляет 20 ± 1 грамм с вероятностью 68% ».
Как подчеркивают сторонники модельных расчетов, выводы из показания приборов к результатам измерений нетривиальны и зависят от множества теоретических и статистических предположений о объект измерения, прибор, окружающая среда и процесс калибровки. Результаты измерения часто достигаются через статистический анализ нескольких показаний, включая предположения о форме распределения показаний и случайность воздействия окружающей среды (Боген и Вудворд 1988: 307–310).Результаты измерений также включают поправки на систематические эффекты, и такие поправки основаны на теоретических предположения относительно работы прибора и его взаимодействия с объектом и окружающей средой. Например, длина измерения необходимо скорректировать для изменения измерения длина стержня с температурой, поправка, которая выводится из теоретического уравнения теплового расширения. Систематический исправления связаны с собственными неопределенностями, например, в определение значений констант, и эти неопределенности оценивается посредством вторичных экспериментов, включающих дальнейшие теоретические и статистические допущения.Более того, неопределенность, связанная с результат измерения зависит от методов, используемых для калибровка прибора. Калибровка требует дополнительных предположения о приборе, калибрующем аппарате, измеряемая величина и свойства эталонов (Ротбарт и Слейден 1994; Франклин 1997; Бэрд 2004: Глава 4; Soler et al. al. 2013). Другой компонент неопределенности происходит из неопределенности в определении измеряемой величины и известен как «Неопределенность определений» (Мари и Джордани, 2013; Греги 2015).Наконец, измерение включает в себя фон предположения о типе весов и системе единиц измерения, и эти предположения часто связаны с более широкими теоретическими и технологическими соображения, касающиеся определения и реализации весов и единицы.
Эти различные теоретические и статистические допущения составляют основу для построения одной или нескольких моделей измерительного процесса. В отличие от математических теорий измерения, где термин «Модель» обозначает теоретико-множественную структуру, которая интерпретирует формальный язык, здесь термин «модель» обозначает абстрактное и локальное представление целевой системы, которая построен на упрощении предположения. [17] Соответствующей целевой системой в этом случае является процесс измерения, то есть система, состоящая из измерительного прибора, объектов или события, подлежащие измерению, окружающая среда (включая людей-операторов), вторичные инструменты и эталоны, эволюция во времени эти компоненты и их различные взаимодействия друг с другом. Измерение рассматривается как набор процедур, цель которых — согласованно присваивать значения параметрам модели на основе прибора показания. Таким образом, модели рассматриваются как необходимые предпосылки для возможность вывода результатов измерения из прибора показания, и как решающие для определения содержания измерения результаты.Как подчеркивают сторонники модельных расчетов, показания, полученные в результате одного и того же процесса измерения, могут использоваться для установить разные результаты измерения в зависимости от того, как процесс измерения моделируется, например, в зависимости от того, в какой среде учитываются влияния, статистические допущения используются для анализа шума, и какие приближения используются при применении фоновая теория. Как говорит Лука Мари,
любой результат измерения содержит информацию, имеющую значение только в контекст метрологической модели, такая модель требуется для включить спецификацию для всех сущностей, которые явно или неявно присутствуют в выражении результата измерения.(2003: 25)
Точно так же говорят, что модели обеспечивают необходимый контекст для оценка различных аспектов качества результатов измерений, включая точность, прецизионность, погрешность и неопределенность (Boumans 2006, 2007a, 2009, 2012b; Мари 2005b).
Основанные на моделях описания расходятся с эмпирическими интерпретациями теории измерений в том, что они не требуют отношений между результаты измерения должны быть изоморфны или гомоморфны наблюдаемым отношения между объектами измерения (Mari 2000).В самом деле, согласно модельным расчетам отношения между измеряемыми объектами вовсе не обязательно быть наблюдаемыми до их измерения (Frigerio et al. al. 2010: 125). Вместо этого ключевое нормативное требование основанной на моделях учетных записей заключается в том, что значения присваиваются параметрам модели в согласованном манера. Критерий согласованности можно рассматривать как сочетание двух подкритерии: (i) согласованность допущений модели с соответствующими фоновые теории или другие существенные предположения о измеряемая величина; и (ii) объективность, i.е. взаимное согласованность результатов измерений по разным измерениям инструменты, окружающая среда и модели [18] (Frigerio et al.2010; Tal 2017a; Teller 2018). Первый подкритерий предназначен для обеспечения того, чтобы предполагаемое количество измеряется, а второй подкритерий предназначен для обеспечения что результаты измерения можно разумно отнести к измеряемым объект , а не какой-то артефакт измерения инструмент, среда или модель.Взятые вместе, эти два требования гарантируют, что результаты измерений остаются действительными независимо от конкретных предположений, связанных с их производства, и, следовательно, контекстная зависимость измерения результаты не угрожают их общей применимости.
7.2 Модели и измерения в экономике
Помимо их применимости к физическим измерениям, модели на основе Анализ также проливает свет на измерения в экономике. Как физический количества, значения экономических переменных часто невозможно наблюдать непосредственно и должны выводиться из наблюдений, основанных на абстрактных и идеализированные модели.Экономист девятнадцатого века Уильям Джевонс за Например, измерять изменения в стоимости золота, постулируя определенные причинно-следственные связи между стоимостью золота, предложением золота и общий уровень цен (Hoover and Dowell 2001: 155–159; Morgan 2001: 239). Как показывает Джулиан Рейсс (2001), Джевонс измерения стали возможны благодаря использованию двух моделей: Теоретико-причинная модель экономики, в основе которой предположение, что количество золота может увеличиться или низкие цены; и статистическая модель данных, основанная на предположение о том, что местные колебания цен взаимно независимы и поэтому взаимно компенсируются при усреднении.Взятый вместе эти модели позволили Джевонсу сделать вывод об изменении значения золота на основе данных об исторических ценах различных товары. [19]
То, как модели функционируют в экономических измерениях, привело к некоторые философы считают определенные экономические модели инструменты сами по себе, аналогично линейкам и весам (Boumans 1999, 2005c, 2006, 2007a, 2009, 2012a, 2015; Morgan 2001). Марсель Буманс объясняет, как макроэкономисты могут изолировать переменная, представляющая интерес от внешних воздействий, путем настройки параметров в модель макроэкономической системы.Этот метод освобождает экономистов от невозможной задачи управления реальной системой. Как Боуман утверждает, что макроэкономические модели функционируют как инструменты измерения, поскольку поскольку они создают инвариантные отношения между входами (показаниями) и выходов (результатов), и насколько эта инвариантность может быть проверена калибровка по известным и стабильным фактам. Когда такие модельные процедуры сочетаются с экспертной оценкой, они могут производить надежные измерения экономических явлений даже вне контроля лабораторные настройки (Boumans 2015: гл.5).
7.3 Психометрические модели и конструктивная валидность
Еще одна область, в которой модели играют центральную роль в измерениях, — это психология. Измерение большинства психологических характеристик, таких как интеллект, тревога и депрессия, не полагаются на гомоморфные отображения типа, поддерживаемого представительной теорией Измерение (Уилсон 2013: 3766). Вместо этого психометрическая теория полагается преимущественно на разработке абстрактных моделей, предназначенных для прогнозировать производительность субъектов в определенных задачах.Эти модели построены на основе существенных и статистических предположений о измеряемый психологический атрибут и его отношение к каждому задача измерения. Например, Теория отклика предмета, популярная подход к психологическому измерению, использует различные модели для оценить надежность и валидность анкет. Рассмотрим анкета, предназначенная для оценки понимания английского языка («способность»), предлагая испытуемым серию да / нет вопросы («предметы»).Одна из самых простых моделей Для калибровки таких вопросников используется модель Раша (Rasch 1960). Эта модель предполагает простое алгебраическое соотношение — известное как «журнал шансов» — между вероятностями что испытуемый ответит на заданный вопрос правильно, сложность конкретный предмет и способности объекта. Новый анкеты калибруются путем проверки соответствия между их указания и предсказания модели Раша и назначение уровни сложности для каждого элемента соответственно.Затем модель используется в в сочетании с анкетой для определения уровня владения английским языком понимание (результаты) из исходных баллов анкеты (показания) (Уилсон 2013; Мари и Уилсон 2014).
Вид статистической калибровки (или «масштабирования») модели Раша дает повторяемые результаты, но часто только первый шаг к полноценному психологическому измерению. Психологов обычно интересуют результаты не ради самого себя, но ради оценки некоторых основных и латентный психологический признак, e.г., понимание английского языка. Хорошего соответствия между ответами на вопросы и статистической моделью пока нет. определить, что измеряет анкета. Процесс установление того, что процедура измеряет предполагаемый психологический атрибут известен как «проверка». Один из способов проверки психометрический инструмент предназначен для проверки того, могут ли различные процедуры, предназначены для измерения одного и того же скрытого атрибута. полученные результаты. Такое тестирование относится к семейству методов проверки. известная как «проверка конструкции».Конструкция — это абстрактное представление скрытого атрибута, предназначенного для измерено, и
отражает гипотезу […] о том, что различные типы поведения коррелируют друг с другом в исследованиях индивидуальных различий и / или аналогично будут затронуты экспериментальные манипуляции. (Nunnally И Бернштейн 1994: 85)
Конструкции обозначаются переменными в модели, которая предсказывает, какие корреляции будут наблюдаться между показаниями различных меры, если они действительно являются показателями одного и того же атрибута.Такой модели включают существенные допущения об атрибуте, в том числе его внутренняя структура и его отношения с другими атрибутами, и статистические допущения о корреляции между различными показателями (Campbell & Fiske 1959; Nunnally & Bernstein 1994: Ch. 3; Angner 2008).
В последние годы философы науки все больше интересуется психометрикой и концепцией валидности. Одна дискуссия касается онтологического статуса латентных психологических атрибутов.Денни Борсбум выступил против операционализма по поводу латентного атрибутов и в пользу определения действительности таким образом, чтобы охватывает реализм: «тест действителен для измерения атрибута, если и только если а) атрибут существует, и б) вариации в атрибута причинно приводят к вариациям в результатах методика измерения »(2005: 150; см. также Hood 2009, 2013; Праздник 2020). Элина Вессонен защищала умеренную форму операционализм по поводу психологических атрибутов и утверждал, что умеренный операционализм совместим с осторожным реализмом (2019).Еще одна недавняя дискуссия посвящена обоснованию разработать процедуры проверки. По словам Анны Александровой, проверка конструкции в принципе является оправданной методологией, поскольку поскольку он устанавливает согласованность с теоретическими предположениями и фоновые знания о скрытом атрибуте. Однако Александрова отмечает, что на практике врачи-психометристы, намеревающиеся измерять счастье и благополучие часто избегают теоретизирования об этих конструирует, а вместо этого апеллирует к народным верованиям респондентов.Это сводит на нет цель проверки конструкции и превращает ее в узкое, техническое упражнение (Александрова, Хайброн, 2016; Александрова 2017; см. также McClimans et al. 2017).
Более фундаментальная критика психометрии заключается в том, что она догматически предполагает, что психологические атрибуты могут быть количественно. Мичелл (2000, 2004b) утверждает, что психометристы не предпринимали серьезных попыток проверить, соответствуют ли указанные атрибуты для измерения имеют количественную структуру, а вместо этого расплывчатое представление об измерении, которое маскирует это пренебрежение.В ответ, Борсбум и Мелленберг (2004) утверждают, что элемент Ответ Теория обеспечивает вероятностные тесты количественной оценки атрибуты. Психометристы, строящие статистическую модель сначала предположить, что атрибут является количественным, а затем подвергнуть модель эмпирическим тестам. В случае успеха такие испытания обеспечивают косвенное подтверждение исходной гипотезы, например к показывая, что атрибут имеет аддитивную объединенную структуру (см. также Vessonen 2020).
Несколько ученых указали на сходство способов моделирования используются для стандартизации измеряемых величин в натуральных и социальные науки.Например, Марк Уилсон (2013) утверждает, что психометрические модели можно рассматривать как инструменты для построения эталоны в том же смысле «измерение эталон », применяемый метрологами. Другие вызвали сомнения по поводу целесообразность и желательность принятия примера естественные науки при стандартизации конструкций в социальных науках. Нэнси Картрайт и Роза Рунхардт (2014) обсуждают «Баллунг» — термин, заимствованный у Отто Нейрата. для обозначения концепций с нечеткой и контекстно-зависимой областью действия.Примеры концепций Баллунга — это раса, бедность, социальная изоляция и качество программ PhD. Такие концепции слишком многогранны, чтобы их измеряется по одной метрике без потери смысла и должен быть представлен либо матрицей индексов, либо несколькими разными меры в зависимости от целей и ценностей (см. также Брэдберн, Картрайт и Фуллер, 2016, Другие интернет-ресурсы). Александрова (2008) указывает, что этические соображения влияют на вопросы об обоснованности мер благосостояния не менее соображения воспроизводимости.Такие этические соображения контекстно-зависимый и может применяться только по частям. В аналогичном vein, Лия МакКлиманс (2010) утверждает, что единообразие не всегда подходящей цели для разработки анкет, поскольку открытость вопросов часто является неизбежным и желательным для получения соответствующая информация от предметы. [20] Переплетение этических и эпистемологических соображений особенно ясно, когда психометрические анкеты используются в медицинских контексты для оценки благополучия и психического здоровья пациентов.В таком случаи, небольшие изменения в дизайне анкеты или анализа его результатов могут принести значительный вред или пользу пациентам (МакКлиманс, 2017; Стегенга, 2018, глава 8). Эти идеи подчеркивают ценностный и контекстуальный характер измерения умственных и социальные явления.
Разработка модельных счетов обсуждалась в предыдущем раздел является частью более крупного «эпистемологического поворота» в философия измерения, возникшая в начале 2000-х гг.Скорее чем упор на математические основы, метафизику или семантика измерения, философская работа последних лет стремится к сосредоточиться на предпосылках и моделях вывода, участвующих в конкретные практики измерения, а также исторические, социальные и материальные размеры измерения. Философское изучение этих темы называют «эпистемологией измерение »(Mari 2003, 2005a; Leplège 2003; Tal 2017a). В самом широком смысле эпистемология измерения — это изучение отношения между измерением и знанием.Центральные темы которые подпадают под сферу эпистемологии измерения, включают условия, при которых измерения производят знания; то содержание, объем, обоснование и пределы таких знаний; то причины, по которым определенные методики измерения и стандартизация успешна или не поддерживает определенные знания претензии, а также отношения между измерениями и другими познавательная деятельность, такая как наблюдение, теоретизирование, экспериментирование, моделирование и расчет.Следуя этим цели, философы опираются на работы историков и социологи науки, занимающиеся измерением практики в течение более длительного периода (Wise and Smith 1986; Latour 1987: Ch. 6; Schaffer 1992; Портер 1995, 2007; Wise 1995; Ольха 2002; Галисон 2003; Gooday 2004; Crease 2011), а также по истории и философия научных экспериментов (Harré 1981; Hacking 1983; Франклин 1986; Картрайт 1999). Следующие подразделы просмотрите некоторые из тем, обсуждаемых в этом быстрорастущем корпусе литература.
8.1 Стандартизация и научный прогресс
Тема, привлекшая значительное внимание философов в последние годы — это выбор и улучшение измерений стандарты. Вообще говоря, стандартизация количественной концепции означает: предписывать определенный способ применения этой концепции к конкретный подробности. [21] Стандартизация измерительного прибора означает оценку того, насколько хорошо результаты измерений этим прибором соответствуют предписанному режиму применение соответствующей концепции. [22] Соответственно, термин «эталон» имеет не менее два значения: с одной стороны, он обычно используется для обозначения абстрактные правила и определения, регулирующие использование количества понятия, такие как определение счетчика. С другой стороны, термин «эталон» также обычно используется для обозначения к конкретным артефактам и процедурам, которые считаются образцовыми применение количественной концепции, такой как металлический стержень, который служил эталонным счетчиком до 1960 г.Эта двойственность смысла отражает двойственную природу стандартизации, которая включает в себя как абстрактные и конкретные аспекты.
В Раздел 4 было отмечено, что стандартизация предполагает выбор среди нетривиальных альтернативы, такие как выбор между различными термометрическими жидкостями или среди разных способов обозначения одинаковой продолжительности. Эти варианты нетривиальные в том смысле, что они влияют на то, температурные (или временные) интервалы считаются равными и, следовательно, влияют на содержат ли утверждения естественного права термин «Температура» (или «время») оказывается верной.Обращение к теории, чтобы решить, какой стандарт более точен, было бы круговой, поскольку теория не может быть однозначно применена к сведения перед выбором эталона. Этот округлость по-разному называли «проблемой координации »(van Fraassen 2008: Ch. 5) и« проблема номических измерений »(Chang 2004: Ch. 2). Как уже упоминалось, конвенционалисты попытались уйти от округлости, постулируя априори утверждений, известных как «координационные определения », которые должны были связать количественные термины с специфические измерительные операции.Недостатком этого решения является то, что он предполагает, что выбор эталона произвольный и статичны, в то время как на практике эталоны обычно выбираются на основе эмпирических соображений и в конечном итоге улучшаются или заменены стандартами, которые считаются более точными.
Новое направление работ по проблеме координации появилось в последние годы, в первую очередь из произведений Хасока Чанга (2001, 2004, 2007; Барвич и Чанг, 2015) и Бас ван Фраассен (2008: Гл.5; 2009, 2012; см. также Padovani 2015, 2017; Мишель 2019). Эти Работы используют исторический и последовательный подход к проблеме. Вместо того, чтобы полностью избегать проблемы округлости, как и их предшественники, они намеревались показать, что округлость не порочный. Чанг утверждает, что построение количественной концепции и Стандартизация его измерения — взаимозависимые и повторяющиеся задачи. Каждая «эпистемическая итерация» в истории стандартизация уважает существующие традиции и в то же время исправляя их (Chang 2004: Ch.5). Донаучная концепция температура, например, была связана с грубым и неоднозначным методы упорядочивания предметов от горячего к холодному. Термоскопы и в конечном итоге термометры помогли изменить первоначальную концепцию и сделали это точнее. С каждой такой итерацией количественное понятие было пересмотрены на более стабильный набор стандартов, которые, в свою очередь, позволили более точно проверить теоретические предсказания, облегчение последующего развития теории и построения более стабильных стандартов и т. д.
Как этот процесс избегает порочной замкнутости, становится ясно, когда мы посмотрим при этом либо «сверху», т.е. в ретроспективе с учетом наших текущие научные знания, или «изнутри», глядя в исторических событиях в их первоначальном контексте (ван Фраассен 2008: 122). С любой точки зрения координация успешна, потому что это увеличивает согласованность между элементами теории и инструментария. Вопросы «что считать количественным измерением X ? » и «какое количество X ?», хотя не имеют ответа независимо друг от друга, адресованы вместе в процессе взаимного совершенствования.Только когда человек принимает фундаменталистской точки зрения и пытается найти отправную точку для координация, свободная от предположений, что этот исторический процесс ошибочно не имеет эпистемического обоснования (2008: 137).
В новой литературе по координации смещается акцент обсуждение от определений количественных терминов к реализаций этих определений. На метрологическом жаргоне «Реализация» — это физический инструмент или процедура, приблизительно удовлетворяет данному определению (ср.JCGM 2012: 5.1). Примеры метрологических реализаций — официальные прототипы килограмм и часы с цезиевым фонтаном, используемые для стандартизации второй. Недавние исследования показывают, что методы, используемые для проектирования, поддерживать и сравнивать реализации имеют прямое отношение к практическое применение понятий количества, единицы и масштаба, не менее чем определения этих понятий (Riordan 2015; Tal 2016). В связь между определением и реализацией единицы становится особенно сложно, когда определение сформулировано теоретически.Некоторые из основных единиц Международной системы (СИ) — включая метр, килограмм, ампер, кельвин и моль — нет больше определяется ссылкой на какой-либо конкретный вид физической системы, но фиксируя численное значение фундаментальной физической постоянной. Килограмм, например, был переопределен в 2019 году как единица массы. такое, что числовое значение постоянной Планка точно равно 6,62607015 × 10 -34 кг м 2 с -1 (BIPM 2019: 131). Понимание килограмма под этим определением — это в высшей степени теоретическая задача.Изучение практической реализации такие подразделения пролили новый свет на развивающиеся отношения между измерения и теория (Tal 2018; de Courtenay et al 2019; Wolff 2020b).
8.2 Теоретическая основа измерения
Как уже обсуждалось выше (разделы 7 и 8.1), теория и измерение взаимозависимы как исторически, так и концептуально. С исторической стороны развитие теории и измерение происходит через итерационные и взаимные уточнения. На концептуальная сторона, спецификация форм процедур измерения эмпирическое содержание теоретических концепций, а теория дает систематическая интерпретация показаний измерений инструменты.Эта взаимозависимость измерения и теории может показаться как угроза доказательной роли, которую измерение должно играть в научном предприятии. В конце концов, результаты измерений думал, что может проверить теоретические гипотезы, и это кажется требуют некоторой степени независимости измерения от теории. Этот угроза особенно очевидна, когда теоретическая гипотеза испытанный уже предполагается как часть модели измерения инструмент. Приведем пример из работы Франклина и др.(1989: 230):
На первый взгляд может показаться, что если кто-то должны были использовать ртутный термометр для измерения температуры объекты как часть эксперимента, чтобы проверить, расширяются ли объекты по мере повышения их температуры.
Тем не менее Франклин и др. сделать вывод, что округлость не беспощадный. Ртутный термометр можно откалибровать по другому термометр, принцип действия которого не предполагает закона теплового расширения, например, газовый термометр постоянного объема, тем самым подтверждая надежность ртутного термометра на независимые основания.В более общем плане, в контексте локальной проверки гипотез угроза замкнутости обычно может быть избегать обращения к другим видам инструментов и другим частям теория.
Другой вид беспокойства по поводу доказательной функции измерения возникает в глобальном масштабе, когда проводится проверка всех теорий. обеспокоенный. Как утверждает Томас Кун (1961), научные теории обычно принимаются задолго до количественных методов их тестирования становятся доступными. Надежность недавно введенного измерения методы обычно проверяются на соответствие предсказаниям теории а не наоборот.По словам Куна, « путь от научного закона к научному измерению редко бывает ехал в обратном направлении »(1961: 189). Например, Закон Дальтона, который гласит, что веса элементов в химические соединения связаны друг с другом целиком пропорции, изначально противоречащие некоторым из наиболее известных мерки таких пропорций. Только предполагая Закон Дальтона, который последующие химики-экспериментаторы смогли исправлять и улучшать свои методы измерения (1961: 173).Следовательно, Кун утверждает, что функция измерения в физических науках не для проверки теории, а для ее применения во все большем объеме и точность, и, в конечном итоге, позволить стойким аномалиям выйти на поверхность это ускорит следующий кризис и научную революцию. Примечание что Кун не утверждает, что измерение не имеет доказательной роли для играть в науку. Вместо этого он утверждает, что измерения не могут проверить теория изолирована, но только в сравнении с альтернативной теорией что предлагается в попытке объяснить обнаруженные аномалии за счет все более точных измерений (для яркого обсуждения диссертации Куна см. Hacking 1983: 243–5).
Традиционные дискуссии о теоретической нагруженности, как и у Куна, были проводится на фоне логических позитивистов различие между теоретическим и наблюдательным языком. В теоретическая нагруженность измерения правильно воспринималась как угроза возможность четкого разграничения между двумя языками. Современные дискуссии, напротив, больше не ведутся. теоретическая нагруженность как эпистемологическая угроза, но принимать как должное что некоторый уровень теоретической нагруженности является предпосылкой для измерений иметь какую-либо доказательную силу.Без некоторого минимального существенного предположения об измеряемой величине, например о ее приемлемости манипулированию и его отношению к другим величинам, это было бы невозможно интерпретировать показания средств измерений и следовательно, невозможно установить доказательную релевантность этих показания. Об этом уже говорил Пьер Дюгем (1906: 153–6; см. также Carrier 1994: 9–19). Более того, современные авторы подчеркивают, что теоретические предположения играют важные роли в исправлении ошибок измерения и оценке погрешности измерения.Действительно, физические процедуры измерения становятся на точнее на , если модель, лежащая в их основе деидеализованный, процесс, который предполагает увеличение теоретических богатство модели (Tal 2011).
Признание того, что теория имеет решающее значение для гарантии Доказательная надежность измерений обращает внимание на «Проблема обоснования наблюдений», которая является обратной вызов традиционной угрозе теоретической нагруженности (Tal 2016b). Задача состоит в том, чтобы указать, какую роль наблюдение играет в измерение, и особенно какая связь с наблюдением необходимо и / или достаточно, чтобы измерение могло сыграть доказательная роль в науках.Эта проблема особенно очевидна, когда одна пытается объяснить растущее использование вычислительных методы выполнения задач, которые традиционно решались измерительные приборы. В роли Маргарет Моррисон (2009) и Венди Паркер (2017) утверждают, бывают случаи, когда достоверная количественная информация собирается о целевой системе с помощью компьютера моделирование, но таким образом, чтобы удовлетворить некоторые из основных Desiderata для измерения, например, эмпирическое обоснование и ретроспективный (см. также Lusk 2016).На такую информацию не полагается по сигналам, передаваемым от конкретного объекта интереса к инструмент, но на использовании теоретических и статистических моделей для обрабатывать эмпирические данные о связанных объектах. Например, данные методы ассимиляции обычно используются для оценки прошлых атмосферных температуры в регионах, где нет показаний термометра. Некоторые методы делают это путем подбора вычислительной модели поведение атмосферы на комбинацию доступных данных из близлежащие регионы и модельный прогноз условий во время наблюдение (Parker 2017).Эти оценки затем используются в различных способов, в том числе в качестве данных для оценки перспективных климатических моделей. Независимо от того, называют ли эти оценки «Измерения», они ставят под сомнение идею о том, что производство надежные количественные данные о состоянии объекта требуют наблюдая за этим объектом, как бы слабо он ни понимал термин «Наблюдение». [23]
8,3 Точность и прецизионность
Два ключевых аспекта надежности результатов измерений: тщательность и точность.Рассмотрим серию повторяющихся весов измерения, выполненные на конкретном объекте с равными руками баланс. С реалистической, «ошибочной» точки зрения, результаты этих измерений точных , если они близки к истинному значению измеряемой величины — в нашем случае истинное соотношение веса объекта к выбранному unit — и с точным значением , если они расположены близко друг к другу. An аналогия, которую часто цитируют, чтобы прояснить различие, основанное на ошибках, — это стрелы стреляют в цель, с точностью, аналогичной близости попадания в яблочко и точность, аналогичная плотности распространения хитов (ср.JCGM 2012: 2.13 и 2.15, Teller 2013: 192). Хотя интуитивно понятный, основанный на ошибках способ выделения различий вызывает эпистемологическую трудность. Принято считать, что точные истинные значения большинства представляющих интерес для науки величин непознаваемым, по крайней мере, когда эти количества измеряются непрерывно напольные весы. Если это предположение выполнено, точность, с которой измеряемые величины не могут быть известны с точностью, а только оценивается путем сравнения неточных измерений друг с другом.И все еще непонятно, почему сходимость неточных измерений должна быть воспринимается как указание на истину. Ведь измерения могли быть страдают от общей предвзятости, которая предотвращает их индивидуальные неточности от компенсации друг друга при усреднении. В отсутствие когнитивный доступ к истинным ценностям, как оценка измерения точность возможна?
Отвечая на этот вопрос, философы извлекли пользу из изучения различные значения термина «точность измерения» как используется практикующими учеными.По крайней мере, пять разных чувств были идентифицированы: метафизические, эпистемологические, операционные, сравнительные и прагматичный (Tal 2011: 1084–5). В частности, эпистемологические или «Основанный на неопределенности» смысл этого термина метафизически нейтрален и не предполагает существования истинных ценностей. Вместо, за точность результата измерения принимается близость согласие между ценностями, разумно отнесенными к данной величине доступные эмпирические данные и базовые знания (см. JCGM 2012: 2.13 Заметка 3; Джордани и Мари 2012; де Куртенэ и Грежис 2017).Таким образом, точность измерения может быть оценена следующим образом: установление устойчивости среди последствий моделей, представляющих различные измерительные процессы (Basso 2017; Tal 2017b; Bokulich 2020; Стейли 2020).
Согласно концепции, основанной на неопределенности, неточность — это особый вид неточности. Например, неточность измерения веса составляет широта разброса ценностей, которые обоснованно приписываются вес объекта с учетом показаний весов и доступные базовые знания о том, как работает баланс, и стандартные веса.Неточность этих измерений заключается в компонент неточности, возникающий из-за неконтролируемых изменений показания баланса при повторных испытаниях. Другие источники неточность, помимо неточности, включает несовершенные исправления систематические ошибки, неточно известные физические константы и неопределенные определения измеряемых величин, среди прочего (см. Раздел 7.1).
Пол Теллер (2018) выдвигает другое возражение против ошибочного понятие точности измерения. Он возражает против предположения, что он называет «реализмом точности измерений», согласно которому в действительности измеримые величины имеют определенные значения.Теллер утверждает что это предположение неверно в том, что касается величин обычно измеряется в физике, потому что любое уточнение определенного значения (или диапазоны значений) для таких величин предполагает идеализацию и следовательно, не может относиться ни к чему в действительности. Например, концепция обычно понимается под фразой «скорость звука в воздух »включает в себя множество неявных идеализаций, касающихся однородность химического состава воздуха, температуры и давление, а также стабильность единиц измерения.Удаление эти идеализации полностью потребуют добавления бесконечного количества детали к каждой спецификации. Как утверждает Теллер, точность измерения следует понимать как полезную идеализацию, а именно как концепция, которая позволяет ученым оценивать согласованность и последовательность среди результатов измерения как будто лингвистическое выражение эти результаты зацепились за все в мире. Точность аналогично идеализированная концепция, основанная на неограниченном и неопределенное определение того, что считается повторением измерения при «тех же» обстоятельствах (Teller 2013: 194).
НОВЫЕ Прайс-листы CHALKBOARD BURST 6 «X 9» для вывески для магазинов 100 Торговля и промышленность Розничная торговля и услуги
НОВЫЕ ПРАЙМ-карты CHALKBOARD BURST 6 «X 9» для вывески для магазинов 100 Бизнес и промышленность Розничная торговля и услугиНОВЫЕ тарифные карточки CHALKBOARD BURST 6 «X 9» для вывески для магазинов 100
100 НОВЫХ ценовых карточек 6 «X 9» CHALKBOARD BURST для вывески магазинов, Вы можете писать на них мелом или цветными маркерами. Вывески 100 НОВЫХ ценовых карточек 6 «X 9» CHALKBOARD BURST для магазинов, НОВЫЕ 6 «X 9» Прайс-карты CHALKBOARD BURST для вывески магазинов 100, Бизнес и промышленность, Розничная торговля и услуги, Деловые вывески.
Мешает ли плохая кредитоспособность вам владеть домом?
TruPath Float ™ — это самая быстрая и самая доступная программа по ремонту ипотечных кредитов в стране.
Почему TruPath Credit? Бесплатная консультация
«Мы уже много лет пытаемся получить кредит. Я был так благодарен за то, что подключился к TruPath. Меня научили тому, что я сделал, чтобы создать свою проблему, и как правильно двигаться вперед.Четкий, пошаговый план с легко достижимыми целями ».
«Моя жена и я были в процессе покупки нашего первого дома, и нам нужно было повысить наш кредитный рейтинг, чтобы претендовать на лучшую ипотеку. Мы не совершали многих классических финансовых ошибок, таких как просрочка платежей, большой остаток на кредитных картах и банкротство, и не знали, как быстро поднять наши результаты. Проработав всего несколько месяцев с Брук Пакстон, мой результат увеличился на 58 баллов !! Мы не можем более настоятельно рекомендовать TruPath Credit.Брук была невероятно знающей и отзывчивой на наши вопросы, а также смогла поднять наши баллы с помощью простых и понятных стратегий. Спасибо, TruPath! »
«TruPath действительно готов помочь. Они действительно знают, как повысить кредитоспособность клиента. Пока клиент следует своему плану действий, его кредитные рейтинги растут ». Щелкните для просмотра видео.
«Я БОЛЬШОЙ сторонник TruPath! Они буквально изменили мой бизнес. Приятно иметь делового партнера, которому я могу доверять.Я — фанат!» Нажмите, чтобы посмотреть видео-отзыв.
«TPC оказал наибольшее влияние на то, чтобы вернуть мой кредит в форму. Я влез в долги и проблемы с кредитами после службы в армии. Мне было нелегко перейти к гражданской жизни. Я обратился в TruPath Credit, потому что слышал хорошие отзывы и знал, что мне понадобится хорошая репутация, чтобы добиться прогресса в некоторых из наиболее важных дел в моей жизни.
Персонал очень услужливый и профессиональный.Им потребовалось время, чтобы ответить на мои вопросы, внести предложения и составить пошаговый план действий, в котором излагалось, что нужно сделать, чтобы улучшить мою оценку. Ремонт кредита не происходит мгновенно, но их план действий сработал на удивление быстро. Прокрастинация была для меня настоящей борьбой, но я рад, что нашел время.
TruPath Credit — это Розеттский камень, позволяющий узнать все преимущества и недостатки. Просто, эффективно и действенно ».
«TruPath был глотком свежего воздуха для меня и моей команды.Мы видим более положительные результаты за меньшее время, а их общение и обслуживание клиентов не имеют себе равных ».
«Ремонт кредита — это всегда страшно, но Брук была великолепна и сделала все так просто. Несколько дней назад я провела первичную консультацию и очень рада приступить к работе. Она ответила на все мои вопросы и многое другое. Я настоятельно рекомендую работать с Брук в TruPath Credit! »
«Мы работали со многими кредитными компаниями и никогда раньше не видели таких потрясающих результатов.TruPath поддерживает нас на протяжении всего процесса ».
«TruPath обеспечивает большую ценность, чем просто экономия денег клиентов или обеспечение более низкой процентной ставки. Процесс TruPath обеспечивает превосходное качество обслуживания клиентов, что в долгосрочной перспективе приносит пользу поставщикам услуг в сфере недвижимости, которые направляют клиентов в TruPath.
«Эти парни классные. Мне так сильно помогло выйти из БК. Я начал примерно в августе 2017 года. Мой кредит за 6 месяцев вырос примерно на 130 пунктов.Это был хороший опыт. Они полезны и знают свое дело. Я очень рекомендую этих ребят. Они помогают с вашим планом действий и следят за вами, а также следят за тем, чтобы вы соблюдали график и делали все, что необходимо для достижения результатов ». 🙂
«Все клиенты, которых мы отправили в TruPath, остались очень довольны своим обслуживанием. Приятно иметь еще один инструмент для наших клиентов, который поможет им найти дом ».
«Очень знающий, очень услужливый и дружелюбный! Когда она не смогла мне помочь, она сообщила мне, что больше не будет взимать с меня плату, но по-прежнему была готова ответить на любые вопросы, которые у меня возникли, чтобы продолжить свой путь к повышению кредитоспособности! »
«Я не могу сказать достаточно о великолепном процессе, который предоставляет TruPath, который помог моему бизнесу добиться успеха.”
«Мне всегда хотелось, чтобы кто-нибудь объяснил мне этот процесс. Я всегда благодарен TruPath Credit и их усилиям не только по устранению отрицательных моментов в моем кредите, но и по обучению меня, как извлечь выгоду из стратегии высокого кредитного рейтинга ».
«Когда я начал работать с ними 6 месяцев назад, мне только что отказали в жилищном кредите, тогда я сделал в точности то, что сказала мне Брук, и на прошлой неделе мой кредитный рейтинг был примерно на 100 пунктов выше, и я не только имел право на покупку дома». кредит, но я получил УДИВИТЕЛЬНУЮ процентную ставку! Они удивительны!!!»
«Они всегда стараются помочь нашему клиенту максимально увеличить свой кредит, чтобы получить возможность попасть в дом своей мечты! Они всегда отзывчивы и общительны с нами и нашими клиентами.”
НОВАЯ карточка с ценами CHALKBOARD BURST 6 «X 9» для вывески магазинов 100
100 — НОВАЯ карточка с ценами 6 «X 9» CHALKBOARD BURST для вывески для магазинов. Вы можете писать на них мелом или цветными маркерами. Состояние :: Новое: Совершенно новый, неиспользованный, неоткрытый, неповрежденный предмет в оригинальной упаковке (где применима упаковка). Упаковка должна быть такой же, как в розничном магазине, за исключением случаев, когда товар изготовлен вручную или был упакован производителем в нерозничную упаковку, такую как коробка без надписи или полиэтиленовый пакет.См. Список продавца для получения полной информации. См. Все определения условий: UPC:: Не применяется,
Сколько это мне будет стоить?
Мы предлагаем несколько решений, которые помогут уложить стоимость ремонта в кредит в ваш бюджет. Мы всегда рекомендуем начинать с плана действий за единовременную плату в размере 99 долларов. Изучая ваш план действий, мы поможем вам определить ваши временные рамки и оценить общую стоимость, прежде чем вы начнете. Посетите нашу страницу часто задаваемых вопросов для получения полного списка часто задаваемых вопросов.
Каких результатов я могу ожидать?
Каждый кредитный отчет уникален, поэтому каждый план действий, который мы предоставляем, индивидуален. Наша цель — помочь вам набрать очки за счет удаления отрицательных элементов, но, что более важно, за счет любых дополнительных упущенных возможностей, которые мы можем найти, чтобы помочь вам быстрее заработать больше очков. Посетите нашу страницу часто задаваемых вопросов для получения полного списка часто задаваемых вопросов.
Что мне может предложить Tru Path Credit?
Хотя отрицательные моменты могут быть одной из причин более низкого кредитного рейтинга, обычно наибольшее количество баллов обнаруживается в областях, о которых потребители не подозревают, что они упускают.Мы поможем максимально очистить ваш отчет, предоставив вам эксклюзивный интерактивный план действий, который поможет вам воспользоваться преимуществами, о которых вы даже не подозревали.
Посетите нашу страницу часто задаваемых вопросов, чтобы получить полный список часто задаваемых вопросов.
Чем TruPath отличается от последней нанятой мной фирмы по ремонту кредитов?
Большинство фирм по ремонту кредитов строго сосредоточены на удалении негативных элементов и имеют бизнес-модели, которые намеренно затягивают этот процесс, чтобы удерживать клиентов, платящих ежемесячно, как можно дольше.Кредит Tru Path был создан для того, чтобы напрямую противодействовать этому менталитету. Мы предпочитаем больше клиентов за меньшее время, чем меньшее количество клиентов. Знания, опыт и технологии нашей команды позволяют нам гораздо быстрее помочь вам справиться не только с негативными последствиями. Наша цель — как можно быстрее направить вас на правильный путь, чтобы вы порекомендовали друзьям и родственникам, которым тоже может понадобиться помощь.
Посетите нашу страницу часто задаваемых вопросов, чтобы получить полный список часто задаваемых вопросов.
НОВАЯ ТАБЛИЧНАЯ ДОСКА 6 «X 9» Прайс-карты для вывески магазинов 100
Винил с теплопередачей Stahls Fashion-LITE HTV Texas Orange 15 дюймов x 5 ярдов, миниатюрные шкафчики для зарядки и хранения сотового телефона ПК.FOXBORO FBM39 P0902UT IT ВХОД / 0-20 мА ВЫХОД 4 АНАЛОГОВЫХ ВХОДА, 4 АНАЛОГОВЫХ ВЫХОДА. Гидравлическая подъемная штанга Ford 2110 4140 4000 4600 2600 4100 2000 3600 3000 4110 3610, жилет безопасности с несколькими карманами и застежкой-молнией, соответствует требованиям высокой видимости класса 2, НОВАЯ ТАБЛИЦА 6 «X 9» ЦЕНОВЫЕ ПЛАТЫ ДЛЯ ВЫВЕСКИ ТИПА 100 , BBC micro : bit Карманный мини-ПК NRF51822 Изучите программирование для начинающих. PHILIPS PCF0330P / 031 DIP28, OMRON C500-BC081 3G2A5-BC081 БАЗОВЫЙ БЛОК ЦП. Michigan Drill Series 550 17/64 HSS Развертка с патроном.HaoFst Variable Adjustable Lab DC Bench Power Cord 0-30V 0-5A US Power Cord, НОВАЯ ТАБЛИЧНАЯ ДОСКА 6 «X 9» Ценовые карточки для вывески магазинов 100 , 175 VITON O-RING 9 «ID X 9-3 / 16 Повторно закрывающийся пластиковый пакет «OD», 7 «x 9», 2 мил, 2000 шт. M_M_S Герметичный металлический экранированный шарикоподшипник SMR85ZZ 5 x 8 x 2,5 мм Выберите марку.Кейс 580 E Super E 4×4 Погрузчик Экскаватор-погрузчик Строительная лопата набор наклеек 580E. 50 упаковок ярлыков «Опасно, не используйте». НОВАЯ карточка с ценами CHALKBOARD BURST 6 «X 9» для вывески магазинов 100 ,
Мы всегда начинаем с бесплатной консультации.Мы хотим, чтобы вы чувствовали себя комфортно, двигаясь вперед.
После регистрации нам нужно будет проверить ваш кредитный отчет. Мы покажем вам, как это сделать, чтобы не повредить ваш счет.
Независимо от того, регистрируетесь ли вы в TruPath Optimize ™ или TruPath Qualify ™, вы получите план действий, который мы построим на основе вашего уникального кредитного файла. Звонок для обзора плана действий обычно занимает около 30 минут.
После того, как мы вместе с вами рассмотрим ваш план действий, если вы участвуете в TruPath Qualify ™, нам потребуется, чтобы вы отправили нам некоторые документы, чтобы оспаривать его от вашего имени.
После того, как мы отправим спор, у кредитных бюро есть 30 рабочих дней для проведения расследования. Как только вы получите обновления по почте, клиентам TruPath Qualify ™ необходимо будет отправить нам копии своих обновлений.
НОВАЯ ТАБЛИЧНАЯ ДОСКА 6 «X 9» Прайс-карты для вывески магазинов 100
НОВЫЕ Прайс-карты CHALKBOARD BURST 6 «X 9» для вывески для магазинов 100, Бизнес и промышленность, Розничная торговля и услуги, Вывески для бизнесаЕсли у вас возникнут вопросы или проблемы, вы всегда можете запланировать время, чтобы поговорить по телефону со своим кредитным специалистом
НОВАЯ карточка с ценами CHALKBOARD BURST 6 «X 9» для вывески магазинов 100
Множество карманов для удовлетворения ваших различных потребностей в дорожном хранилище, США Large = Китай X-Large: длина: 29, прочный устойчивый к царапинам металл, 5/16 «4-ФЛЕЙТНАЯ ОДНОКОНЕЧНАЯ Твердосплавная концевая фреза 5/16» X 5/16 «X 7/8» X 2-1 / 2 «, 16 одинарных завитков со звездообразным картоном черного цвета.СНОСКИ: Сделаны на заказ специально для Вас. Материал: 100% полиэстер, холст — легкий. 3 шт. С шестигранным хвостовиком на 1/4 3/8 1/2 дюйма Набор адаптеров для ударных отверток. Купите Beautife Women Off Shoulder с длинным рукавом вязаные свободные пуловеры большого размера и другие пуловеры в AMPRO T20754 1/2 Drive с гибкой Т-образной ручкой, регулируемой переключающей планкой — торцевые ключи -. Блестящие серебряные ленты ловят свет и заставляют праздник сиять, Оригинальная 10,4-дюймовая ЖК-панель nl10276bc20-04 для NEC 1024 * 768, резьбонарезные винты разрезают стенку отверстия, чтобы создать резьбу, Винтажный резной шарм фига из оникса с твердым 10k золотой залог и прыжковое кольцо.1шт MC68000P8 CPU Винтажный микропроцессор IC Новый, он будет упакован в подарочную коробку внутри струнного мешка для розыгрыша, с Рождеством Христовым svg файлы для лазерной резки лазерная резка ЧПУ Лазерная резка игрушек оленей и лосей на Рождество. Размеры вы можете увидеть на картинках. Если вам нужен другой размер. DC 5V 9V 12V 24V Изоляция оптопары 1-канальный релейный модуль триггера уровня H / L, зависит от предметов, отправляемых для резки и шитья.Девушка с длинной косой, завершенное изображение Crewel — Jiffy, комплекты кабелей 15 см, продавец из Великобритании Micro JST 1,25 мм, трехсторонний мужчина и женщина 15 см, излучающий безусловную любовь и заботу, он помогает вам привлечь позитив. ******* Что мне нужно знать, когда вы проверяете *********. Комплекты шестигранных головок из нержавеющей стали диаметром 2 мм А2 Установочные винты Точка чашки M2. Эти шорты, изготовленные Arorac в 1970-х годах, сделаны из ткани, которая изначально использовалась в качестве винтажного наволочки. * ВИНТАЖ * Термостат Honeywell T87F 5-1 / 2 «Настенная пластина золотого цвета V129, см. Фото деталей для чипов на конце двух бусинок, аккумулятор Xbox One 2×2550 мАч Аккумулятор для Xbox One / Xbox One S / Xbox One X / Xbox One Беспроводной контроллер Elite (аккумулятор и зарядное устройство, двухосная шаговая карта Control Technology Corporation CTC 2206-2, установка гвоздей: подходит для неровной поверхности, способствует заживлению раны, 21 почтовое устройство для конвертов с поли пузырчатой подушечкой PBM-2 ID 8 1/2 x 11 Дюймы.Если у вас есть любимый игрок, которого вы хотели бы видеть в кадре. Скатывающийся фильм Скотта Проспекта: Автомобиль и мотоцикл — отличный подарок для любого футбольного фаната. а также может стать отличным подарком.
NEW 6 «X 9» Прайс-карты CHALKBOARD BURST для вывески магазинов 100На них можно писать мелом или цветными маркерами.
Chrysler 200 2015 года пытается вернуть автомобили Pentastar в нужное русло [w / videos]
The Canadian Press
Видение на совместном экране: встреча Байдена и Трюдо, чтобы выявить точки соприкосновения, старые раздражители
ВАШИНГТОН — Назовите это общим экраном Саммит.Двусторонняя встреча премьер-министра Джастина Трюдо и президента Джо Байдена во вторник — дело сугубо виртуальное, благодаря COVID-19 — вселяет надежду на новый старт для Canada-U. С. отношения. Это будет первая встреча нового президента с иностранным лидером и первый шанс Трюдо продвинуть канадские интересы в Белом доме без хаоса и беспокойства последних четырех лет. И хотя пандемия может привести к тому, что ее масштабы не будут такими же, как у Брайана Малруни на Саммите Шемрока 1985 года с Рональдом Рейганом, ожидания в Канаде все еще высоки.Будут ли они встречены, остается только гадать. «Я не хочу, чтобы люди почивали на лаврах и говорили:« Ну, у нас первая встреча, и это очень хорошо для нас », — сказала Мэрискотт Гринвуд, генеральный директор Канадско-американского делового совета. Впереди много тяжелой работы, в том числе и на Canada-U. С. граница, ориентируясь на американский протекционизм, путь вперед в Китае и острый вопрос трансграничных трубопроводов. По словам Гринвуда, для достижения прогресса канцелярия премьер-министра могла бы сделать вид, что Дональд Трамп по-прежнему является президентом.«Канада взяла на себя очень, очень дальновидную, активистскую повестку дня по взаимодействию с США внутри и за пределами округа Колумбия». когда Трамп был у власти, сказала она. «Будет важно иметь такой уровень срочности и такой уровень усилий, а не просто предполагать, что теперь все хорошо, когда здесь Байден». Байден обозначил жесткую позицию в отношении Buy American, своего комплекса протекционистских мер, направленных на обеспечение того, чтобы отечественные подрядчики и поставщики были основными бенефициарами налоговых долларов США, потраченных на инфраструктурные проекты и усилия по закупкам.Он может занять аналогичную линию с Трюдо, предположила в понедельник пресс-секретарь Белого дома Джен Псаки. «Он подписал распоряжение; мы, конечно, оцениваем компоненты закупок, но никаких изменений не ожидается», — сказал Псаки. «Конечно, премьер-министр поднимет все, что он хотел бы сказать, как и любая двусторонняя встреча». Псаки предложил знакомые бромиды — общее видение изменения климата, трансграничных экономических связей и «прочного и глубокого партнерства» между двумя «соседями, друзьями и союзниками по НАТО».«Но она не стала говорить, будет ли Байден продолжать содействовать освобождению канадцев Майкла Коврига и Майкла Спавора, которые содержатся в Китае более двух лет. Эти двое были задержаны после того, как Канада арестовала финансового директора Huawei Мэн Ваньчжоу с целью грозит экстрадиция в США, где ей предъявлено обвинение в нарушении санкций в отношении Ирана. Разрешение возникшего трехстороннего дипломатического противостояния будет для Трюдо главным приоритетом, сказал Эрик Миллер, канадско-американский эксперт и президент D.Компания C. из Rideau Potomac Strategy Group. По его словам, Олимпийские игры 2022 года, которые будут проходить в Пекине, могут стать идеальным поворотным моментом, особенно если у китайцев есть основания опасаться крупных протестов в момент национальной гордости. «Что собираются делать китайцы, если канадская команда выйдет на стадион с повязками на рукавах с надписью« Освободите Майклз »?» — сказал Миллер. «Я действительно думаю, что Байден сейчас находится на той стадии, когда есть некоторая восприимчивость к некоторым другим идеям. И, как это часто бывает с этим материалом, Канада часто выпадает, чтобы как бы толкать иглу.Кстати об иглах: многие ожидают, что Трюдо будет настаивать на том, чтобы Байден сделал больше вакцин против COVID-19, поставляемых в США, на экспорт в Канаду, где задержки производства в Европе мешают попыткам получить огнестрельное оружие. Однако в политическом плане это будет Байдену будет трудно продать идею оказания помощи другим странам, когда усилиям по вакцинации дома еще предстоит пройти долгий путь. «По сути, у Трюдо нет другого выбора, кроме как приложить усилия, — сказал Миллер». Трюдо будет много спрашивать, и люди Байдена обязуются разобраться в этом, и ничего не произойдет.«Ищите аналогичный результат, если Трюдо будет жаловаться на решение Байдена отменить трансграничное расширение трубопровода Keystone XL, которое он сделал росчерком пера в свой первый день в Белом доме. Канада остается страной, в значительной степени зависящей от своего естественного происхождения. ресурсов, сказал Билл Рейли, который с 1989 по 1993 год занимал пост главы Агентства по охране окружающей среды при бывшем президенте Джордже Буше. «Очень вероятно, что возникнут проблемы, которые противоречат некоторым экологическим чаяниям, которые вдохновляют администрацию Байдена», Рейли сказал на панельной дискуссии в понедельник.«Я не думаю, что некоторые из этих проблем поддаются легкому разрешению».

 Улыбнитесь!
Улыбнитесь! (Величина.)
(Величина.)
 )
) )
) )
) )
) )
) )
) Как можно это сделать по схеме? (Зная, что в 1 см 10 мм, а в одном дм 10 см, надо 10 умножить на 10, получиться, что в 1 дм – 100 мм.)
Как можно это сделать по схеме? (Зная, что в 1 см 10 мм, а в одном дм 10 см, надо 10 умножить на 10, получиться, что в 1 дм – 100 мм.)


 )
)
 Г. Петерсон — Номинация 3 — КОНКУРС ЭОР 2013 — Каталог файлов
Г. Петерсон — Номинация 3 — КОНКУРС ЭОР 2013 — Каталог файлов