10 класс. Алгебра
Главная » 10 класс. Алгебра.
10 класс. Алгебра.
Формулы приведения
115.6k.
Формулы приведения относятся к тригонометрической функции, которая использует периодичность для преобразования
10 класс. Алгебра.
10.3.0. Вычисление производных
013.4k.
На этом занятии мы будем учиться применять формулы и правила дифференцирования. Примеры. Найти производные функций.
10 класс. Алгебра.
10.2.6. Решение тригонометрических неравенств. Часть 6
02.6k.
На предыдущих занятиях мы решали тригонометрические неравенства следующих видов: sint<a (10.
10 класс.
Алгебра.
10.2.5. Решение тригонометрических неравенств. Часть 5
12.6k.
На предыдущих занятиях мы решали графическим способом тригонометрические неравенства вида: sint<
10 класс. Алгебра.
10.2.4. Решение тригонометрических неравенств. Часть 4
01.8k.
На предыдущих трех занятиях по решению тригонометрических неравенств графическим способом мы рассмотрели
10 класс. Алгебра.
10.2.3. Решение тригонометрических неравенств. Часть 3
01.9k.
На предыдущих двух занятиях по решению тригонометрических неравенств графическим способом мы рассмотрели
10 класс. Алгебра.
10.2.2. Решение тригонометрических неравенств.
Часть 2
01.5k.
На прошлом занятии «10.2.1. Решение тригонометрических неравенств. Часть 1» мы решили три
10 класс. Алгебра.
10.2.1. Решение тригонометрических неравенств. Часть 1
01.6k.
На этом и последующих занятиях мы будем решать графическим способом тригонометрические неравенства одного
10 класс. Алгебра.
10.3.1. Уравнение касательной
114.2k.
Выведем уравнение касательной к графику функции y=f (x) в точке с абсциссой х0. Для наглядности используем
10 класс. Алгебра.
10.3. Производная и ее геометрический смысл
113.8k.
В координатной плоскости хОу рассмотрим график функции y=f (x).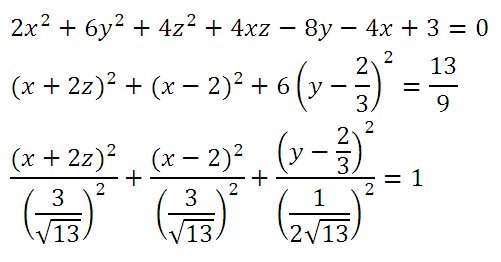
Зафиксируем точку М(х0; f (x0)).
Алгебра 10 класс. Углублённый уровень. Интерактивный курс
Алгебра и начала анализа 10 класс. Углублённый уровень
Учебный онлайн курс по предмету Алгебра и начала анализа 10 класс. Углублённый уровень сможет заменить бумажный учебник или дополнить его. Содержание интерактивных онлайн-курсов соответствует требованиям федеральных государственных образовательных стандартов (ФГОС).
Онлайн уроки построены таким образом, что перед изучением новой темы, предлагается повторить и закрепить ранее изученный материал Алгебра 9 класса.
Онлайн уроки учебного онлайн курса по предмету Алгебра и начала анализа 10 класс. Углублённый уровень подходят для самостоятельного изучения. Ребенок познакомится с теорией, проверит полученные знания с помощью онлайн-тренажеров и интерактивных заданий, подготовится к контрольным и проверочным работам, экзаменам, ОГЭ и ЕГЭ.
Такой формат занятий поможет разобраться в новой теме или подтянуть знания по предмету.
Доступ к онлайн урокам осуществляется через интернет (24/7).
Наш сборник — это способ улучшить успеваемость, начать подготовку к экзаменам, повторить пройденный материал во время каникул.
В качестве одной из составляющей курса, ученикам доступен объемный дополнительный материал, позволяющий углубить имеющиеся знания. Различные типы заданий, представленные в онлайн-учебнике — одна из важных составляющих подготовки к будущим экзаменам.
Главными целями изучения предмета являются:
- обеспечение возможности успешного продолжения образования по специальностям, связанным с прикладным использованием математики;
- формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;
- развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, а также последующего обучения в высшей школе;
- овладение математическими знаниями и умениями, необходимыми в повседневной жизни для изучения школьных естественнонаучных дисциплин на базовом уровне, для получения образования в областях, не требующих углублённой математической подготовки;
- воспитание средствами математики культуры личности, понимания значимости математики для научно-технического прогресса, отношения к математике как к части общечеловеческой культуры через знакомство с историей развития математики.
Оглавление
Занятие 1. Многочлены от одной переменной
Интернет-урок 1. Основные определения и свойства многочленов. Деление многочленов с остатком
Интернет-урок 2. Алгоритм Евклида для многочленов
Интернет-урок 3. Теорема Безу. Теорема о рациональных корнях многочлена
Интернет-урок 4. Решение целых рациональных уравнений методом разложения на множители и методом неопределённых коэффициентов
Интернет-урок 5. Решение целых рациональных уравнений методом замены переменной. Возвратные уравнения
Занятие 2. Тематическая контрольная работа № 1. Многочлены от одной переменной
Занятие 3. Понятие угла и тригонометрические формулы
Интернет-урок 1. Углы и их меры
Интернет-урок 2. Определение синуса, косинуса, тангенса и котангенса для углов прямоугольного треугольника. Табличные значения
Интернет-урок 3. Формулы для суммы и разности углов
Интернет-урок 4.
Формулы для двойных и половинных углов
Интернет-урок 5. Формула для введения дополнительного аргумента
Интернет-урок 6. Формулы для суммы и разности синусов и косинусов, формулы для их произведений
Занятие 4. Тематическая контрольная работа № 2. Понятие угла и тригонометрические формулы
Занятие 5. Тригонометрические уравнения и неравенства
Интернет-урок 1. Арккосинус, арксинус, арктангенс и арккотангенс. Решение простейших тригонометрических уравнений и неравенств
Интернет-урок 2. Способы отбора корней в тригонометрических уравнениях
Интернет-урок 3. Решение тригонометрических неравенств графическим способом. Системы тригонометрических уравнений и неравенств
Интернет-урок 4. Решение тригонометрических уравнений, которые заменой сводятся к алгебраическим
Интернет-урок 5. Однородные тригонометрические уравнения, разложения на множители, специальные замены переменной
Интернет-урок 6. Использование ограниченности функций при решении тригонометрических уравнений
Интернет-урок 7.
Интернет-урок 8. Практические задачи с применением тригонометрии
Занятие 6. Тематическая контрольная работа № 3. Тригонометрические уравнения и неравенства
Занятие 7. Понятие об обратных тригонометрических функциях
Интернет-урок 1. Обратные тригонометрические функции
Интернет-урок 2. Операции над обратными тригонометрическими функциями
Занятие 8. Показательная функция и уравнения
Интернет-урок 1. Степенная функция с натуральным и целым показателем. Степени и корни
Интернет-урок 2. Понятие логарифма. Свойства логарифмов
Интернет-урок 3. Степенная и показательная функции. Решение простейших показательных уравнений
Интернет-урок 4. Методы решения показательных уравнений: уравнивание показателей, вынесение общего множителя за скобки, введение новой переменной, деление на показательную функцию
Занятие 9.
Тематическая контрольная работа № 4. Показательная функция и уравнения
Занятие 10. Методы решения показательных уравнений
Интернет-урок 1. Сведение показательного уравнения к алгебраическому заменой переменной
Интернет-урок 2. Однородные уравнения относительно показательных функций
Интернет-урок 3. Показательные уравнения на взаимообратных числах
Интернет-урок 4. Решение показательных уравнений функционально-графическим методом
Интернет-урок 5. Методы решения, связанные с разложением на множители
Интернет-урок 6. Сложные показательные уравнения
Занятие 11. Тематическая контрольная работа № 5. Методы решения показательных уравнений
Занятие 12. Показательные неравенства
Интернет-урок 1. Простейшие показательные неравенства
Интернет-урок 2. Сведение неравенства к алгебраическому заменой переменной
Интернет-урок 3. Неравенства, содержащие однородные функции относительно показательных функций и построенные на взаимообратных числах
Занятие 13.
Тематическая контрольная работа № 6. Показательные неравенства
Занятие 14. Логарифмические уравнения
Интернет-урок 1. Логарифмическая функция, её свойства и график. Преобразование логарифмических выражений
Интернет-урок 2. Решение логарифмических уравнений функционально-графическим методом
Интернет-урок 3. Простейшие логарифмические уравнения
Интернет-урок 4. Логарифмические уравнения, сводимые заменой к алгебраическим
Интернет-урок 5. Уравнения, содержащие однородные функции относительно логарифмических функций и построенные на взаимообратных числах
Интернет-урок 6. Логарифмические уравнения на последовательное применение нескольких методов
Занятие 15. Тематическая контрольная работа № 7. Логарифмические уравнения
Занятие 16. Логарифмические неравенства
Интернет-урок 1. Простейшие логарифмические неравенства
Интернет-урок 2. Логарифмические неравенства, сводимые заменой переменных к алгебраическим
Интернет-урок 3.
Решение логарифмических неравенств с переменным основанием
Занятие 17. Тематическая контрольная работа № 8. Логарифмические неравенства
Занятие 18. Системы уравнений и неравенств
Интернет-урок 1. Системы показательных уравнений. Системы логарифмических уравнений
Интернет-урок 2. Показательные и логарифмические системы неравенства
Интернет-урок 3. Смешанные системы уравнений
Интернет-урок 4. Смешанные системы неравенств
Занятие 19. Тематическая контрольная работа № 9. Системы уравнений и неравенств
Занятие 20. Системы линейных уравнений
Интернет-урок 1. Системы линейных уравнений с двумя неизвестными. Метод Гаусса
Интернет-урок 2. Текстовые задачи на системы линейных уравнений
Занятие 21. Графики функций
Интернет-урок 1. Обзор элементарных функций и их графиков
Интернет-урок 2. Построение графиков функций с помощью преобразований
Занятие 22.
Тематическая контрольная работа № 10. Графики функций
Занятие 23. Элементы логики. Множества
Интернет-урок 1. Высказывания и операции над ними. Неопределенные высказывания. Знаки общности и существования
Интернет-урок 2. Некоторые приемы доказательства
Вопросы по практике алгебры для класса 10
Вопрос 1:
Найдите квадратный корень 289x 4 −612x 3 + 970x 2 −684x + 361.
Решение:
. 2 :Решить √(y + 1) + √(2y −5) = 3
Решение :
√(y + 1) + √2(2y −5) = 9 3 √ 0004 900 (y + 1) = 3 — √(2y −5)
Взятие квадратов с обеих сторон
[√ (y + 1)] 2 = [3 — √ (2y −5)] 2
(y + 1) = 9 — 6 √ (2y −5) + (2y — 5)
y + 1 — 2y + 5 — 9 = — 6 √ (2y −5)
— Y — 3 = — 6 √(2y −5)
[- (y + 3)] 2 = [ — 6 — 6 √9000]0007 2
y 2 + 6y + 9 = 36 (2y — 5)
Y 2 + 6y — 72y + 9 + 180 = 0 0004 + 6y — 72y + 9 + 180 = 0 0004 + 6y — 72y + 9 + 180 = 0 0004 + 6y — 72y + 9 + 180 = 0 0004 .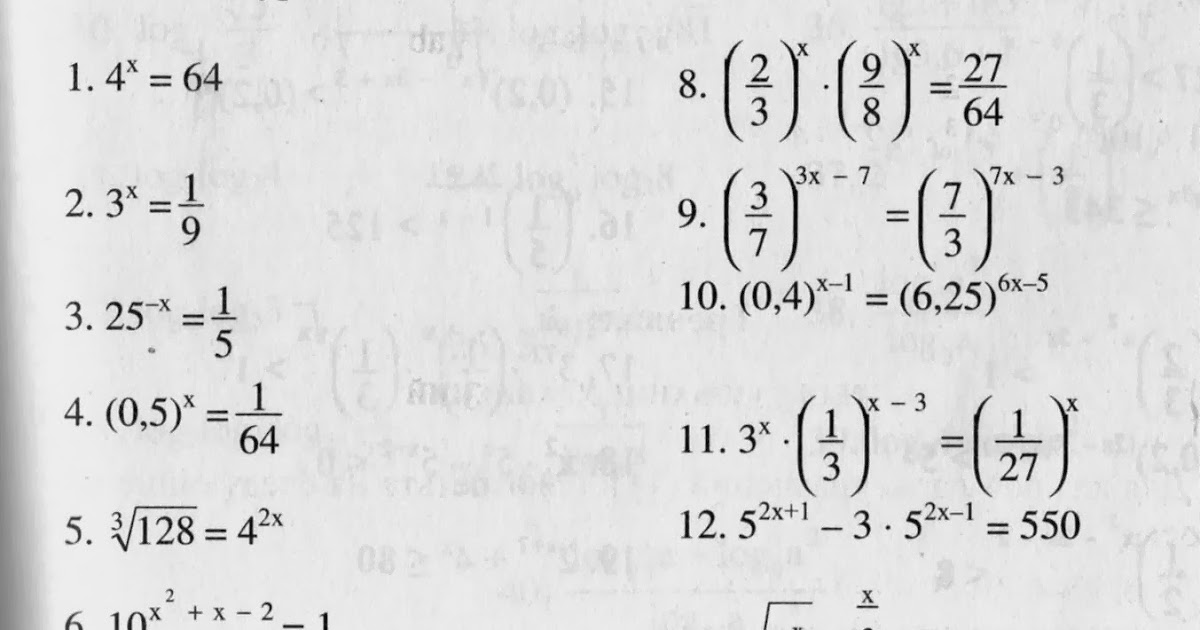
y 2 — 66y + 189 = 0
(Y -63) (Y -63) (Y -63) (Y -63) (Y -63) (Y -63) (Y -63) (Y -63).y = 63 и Y = 3 2 Вопрос 3:
. Лодка доставляет 1,6000. реке, чем вниз по реке. Какова скорость лодки в стоячей воде, если скорость течения 4 км/ч?
Решение :
Пройденное расстояние = 36 км
Пусть «x» будет скоростью лодки
Пусть «y» будет скоростью потока = 4 км
Скорость вниз по течению = x + y = x + 4
Скорость вверх по течению = x — y = x — 4
Затраченное время = 1,6 часа
Время = Расстояние / Скорость
Время, затраченное на движение вверх по течению = 36/(x — 4) —(1)
Время, затраченное на движение вниз по течению = 36/(x + 4) —(2)
(1) ) + (2)
36[1/(x — 4) — 1/(x + 4)] = 1,6
x + 4 — x + 4/(x + 4)(x — 4) = 1,6/ 36
8/(х 2 — 16) = 16/360
2880 = 16 (x 2 — 16)
2880 = 16x 2 — 256
2880 + 256 = 16x 2
16x 2 = 3136 x 2 = 196 x = 14 Отсюда скорость лодки 14 км/ч. Вопрос 4 : Можно ли запроектировать прямоугольный парк с периметром 320 м и площадью 4800 м 2 ? Если да, то найдите его длину и ширину. Решение : Периметр прямоугольного парка = 320 м Площадь парка = 4800 2(l + b) = 320 l + b 0 0 0 120—0 0 0 120—0 0 4800 l = 4800/b Применяя значение l из (1), получаем (4800/b) + b = 160 (4800 + b 2 )/b = 02 900 9000 4800 + b 2 = 160b b 2 — 160b + 4800 = 0 (b — 120)(b — 40) = 0 b = 120 и b = 40 Если b = 120, то l = 4800/120 = 40 Если b = 40, то l = 4800/40 = 120 м. Помимо всего вышеперечисленного, если вам нужны какие-либо другие материалы по математике, воспользуйтесь нашим пользовательским поиском Google здесь. Пожалуйста, отправьте свой отзыв на [email protected] Мы всегда ценим ваши отзывы. ©Все права защищены. (1) Решить (1/3) (x + y −5) = y − z = 2x −11 = 9−(x +2z) Решение (2) В школу принимают сто пятьдесят учеников. Они распределяются по трем секциям A, B и C. Если 6 студентов переводятся из секции A в секцию C, в секциях будет равное количество студентов. Если количество учащихся секции С в 4 раза превышает количество учащихся секции А на количество учащихся секции Б, найти количество учащихся в трех секциях. Решение (3) В трехзначном числе, когда цифры десятков и сотен переставлены местами, новое число в 54 раза больше исходного числа более чем в три раза. Если к номеру добавить 198, цифры меняются местами. Цифра десятков превышает цифру сотен в два раза, так как цифра десятков превышает цифру единиц. Найдите исходное число. Решение (4) Найдите наименьшее общее кратное xy(k 2 +1)+k(x 2 + y 2 ) и xy(k 2 −1)+k (x 2 -y 2 ) Решение (5) Найдите GCD следующего по алгоритму деления 2x 4 +13x 3 +27x 2 + 23x + 7 , x 3 + 3x 2 + 3x + 1 , x 2 + 2x + 1 Решение (6) Приведите заданные выражения Rational к наименьшей форме 90i (x 3a — 8)/(x 2a + 2x a + 4) Решение (ii) (10x 3 — 25x 2 + 4x — 10)/( — 4 — 10x 2 ) Решение (7) Упростите Решение (8) Arul, Ravi and Работая вместе, Рам может очистить магазин за 6 часов. (9) Найти квадратный корень из 289x 4 -612x 3 + 970x 2 −684x + 361. Решение (10) Решить √(y + 1) + √(2y −5) = 3 км вверх по реке, чем вниз по реке. Какова скорость лодки в стоячей воде, если скорость течения 4 км/ч? Решение (12) Можно ли спроектировать прямоугольный парк с периметром 320 м и площадью 4800 м 2 ? Если да, то найдите его длину и ширину. Решение (13) В t минут после 14:00 время, необходимое до 15:00, на 3 минуты меньше, чем t 2 /4. Найдите т. Решение (14) Количество мест в ряду равно общему количеству рядов в зале. Общее количество мест в зале увеличится на 375, если количество рядов увеличить вдвое, а количество мест в каждом ряду уменьшить на 5. (15) Если a и b — корни многочлена f(x) = x 2 −2x + 3, найдите многочлен, корни которого равны (i) α + 2, β + 2 Решение (ii) (α — 1)/(α + 1), (β — 1)/ (β + 1) Решение (16) Если –4 является корнем уравнения x 2 + px −4 = 0 и если уравнение x 2 + px +q = 0 имеет одинаковые корни, найдите значения p и q. Решение (17) Два фермера Сентил и Рави выращивают три сорта зерновых, а именно рис, пшеницу и раги. Если продажа (в ₹) трех сортов зерна обоими фермерами в апреле задается матрицей. , а распродажа в мае (в ₹) ровно в два раза больше, чем распродажа в апреле для каждого сорта. (i) Каков средний объем продаж в апреле и мае. (ii) Если объем продаж продолжает увеличиваться таким же образом в последующие месяцы, каким будет объем продаж в августе? Solution (18) Solution (19) Given Solution (20) Solution Solution .
onlinemath5all.com Рабочий лист с задачами по алгебре для 10 класса
Работая в одиночку, Рави тратит на уборку магазина в два раза больше времени, чем Арул. Раму нужно в три раза больше времени, чем Арулу. Сколько времени потребуется каждому, если они будут работать в одиночку? Решение
Найдите количество рядов в зале в начале Решение