Ответы по алгебре 10 класс макарычев: Решебник по алгебре за 10 класс Арефьева, ГДЗ 2019-2020

ГДЗ По Алгебре 10 Класс Макарычев Миндюк – Telegraph

➡➡➡ ПОДРОБНЕЕ ЖМИТЕ ЗДЕСЬ!

ГДЗ По Алгебре 10 Класс Макарычев Миндюк

ГДЗ по алгебре 10 класс . Алгебра 10 -11 класс учебник и задачник Базовый уровень .  Решебники по алгебре для 10 класса помогут вспомнить ранее пройденный материал, а также научиться работать с тригонометрическими функциями . 

ГДЗ (решебники) по алгебре . Алгебра 7 класс .  Алгебра 10 класс . Арефьева И . Г ., Пирютко О . Н . 2020  

С ГДЗ ! Пользуйся готовыми решениями домашних заданий , содержащихся в пособии, и тебе будут не страшны любые задания! С готовыми результатами и подробно расписанными решениями ты справишься с любой самостоятельной или контрольной работой в классе . 

Использование готовых домашних заданий по алгебре 10 класс выгодно с той точки зрения, что не нужно будет тратить кучу времени на прорешивание каждого задания, а будет достаточно получить ответ в режиме онлайн в любое время .  

Алгебра 10 класс Мерзляк А .Г . Базовый уровень .  Теперь ученик сможет быстро подготовиться к контрольной работе, а также заранее проверить правильность выполнения домашнего задания, что позволит получить максимально высокие баллы по предмету и повысить . . 

· Макарычев Ю .Н ., Миндюк Н .Г ., Нешков К .И, Феистов И .Е . Алгебра , 9 класс, Мнемозина; · Мордкович А .Г ., Николаев Н .П ./ Мордкович А .Г ., Семенов П .В  Сборник задач по алгебре . Часть 2 . Иррациональные, триго-нометрические, логарифмические уравнения и неравенства . 

Мегарешеба — Белорусские ГДЗ и Решебник по Алгебре поможет Вам найти ответ на самое сложное задание для 10 класса . Решай онлайн домашку вместе с нами! 

ГДЗ (решебники) — подробные готовые домашние задания Алгебра 10 класс .  Сущность и целевое назначение решебника по алгебре за 10 класс . Вам нужна помощь алгебры? Мы знаем, как ответить: «ГДЗ по алгебре 10 класс» – оптимальное решение для школьников, их . . 

ГДЗ по алгебре . 7 класс 8 класс 9 класс 10 класс 11 класс .  ГДЗ по алгебре — это что вы найдете здесь . Если Вы здесь именно за этим — тогда добро пожаловать .  Ни кто не заставляет 100% и постоянно переписывать с ГДЗ по алгебре, но признайтесь бывают моменты когда . . 

Алгебра 10 класс . Контрольные работы .  Внимательный подход к каждой теме должен помочь школьникам уяснить суть изучаемого материала, но в качестве подсобного средства всегда можно воспользоваться ГДЗ по алгебре 10 класс, который очень прост в использовании . 

ГДЗ для 10 класса по предмету «Алгебра » . Многие школьники считают, что знание алгебры не пригодится им в дальнейшей жизни, ведь все эти формулы мало где можно применить . Однако даже работа программиста требует определенного понимания алгебраических уравнений, не . . 

Используя готовые домашние задания по алгебре для 10 класса , ученик сможет зосто решить любой пример не только из учебника, но и аналогичный из учительского сборника . В решебе по алгебре каждое задание разобрано до мельчайших деталей, что позволяет . . 

Готовые домашние задания по алгебре — 7 класс — Сапожников А .А . — к учебнику Алгебра 7 класс — Алимов Ш .А .  ГДЗ по алгебре для 9 класса 2009 к «Алгебра : учебник для 9 класса общеобразовательных учреждений, Макарычев Ю .Н ., Миндюк Н .Г ., Нешков К .И ., Суворова . . 

Готовые домашние задания .  Учебники по алгебре 10 класс скачать в pdf бесплатно . 

Алгебра – очень нелегкий предмет, именно поэтому, практически каждому ученику просто необходим помощник . Имея три главы с уникальными решениями задач, ГДЗ стали незаменимым атрибутом учеников . Каждый раздел рассматривает свой спектр вопросов . . 

ГДЗ по алгебре 10 класс . Алгебра 10 -11 класс учебник и задачник Базовый уровень .  Решебники по алгебре для 10 класса помогут вспомнить ранее пройденный материал, а также научиться работать с тригонометрическими функциями . 

ГДЗ (решебники) по алгебре . Алгебра 7 класс .  Алгебра 10 класс . Арефьева И . Г ., Пирютко О . Н . 2020  

С ГДЗ ! Пользуйся готовыми решениями домашних заданий , содержащихся в пособии, и тебе будут не страшны любые задания! С готовыми результатами и подробно расписанными решениями ты справишься с любой самостоятельной или контрольной работой в классе .  

Использование готовых домашних заданий по алгебре 10 класс выгодно с той точки зрения, что не нужно будет тратить кучу времени на прорешивание каждого задания, а будет достаточно получить ответ в режиме онлайн в любое время . 

Алгебра 10 класс Мерзляк А .Г . Базовый уровень .  Теперь ученик сможет быстро подготовиться к контрольной работе, а также заранее проверить правильность выполнения домашнего задания, что позволит получить максимально высокие баллы по предмету и повысить . . 

· Макарычев Ю .Н ., Миндюк Н .Г ., Нешков К .И, Феистов И .Е . Алгебра , 9 класс, Мнемозина; · Мордкович А .Г ., Николаев Н .П ./ Мордкович А .Г ., Семенов П .В  Сборник задач по алгебре . Часть 2 . Иррациональные, триго-нометрические, логарифмические уравнения и неравенства . 

Мегарешеба — Белорусские ГДЗ и Решебник по Алгебре поможет Вам найти ответ на самое сложное задание для 10 класса . Решай онлайн домашку вместе с нами! 

ГДЗ (решебники) — подробные готовые домашние задания Алгебра 10 класс .   Сущность и целевое назначение решебника по алгебре за 10 класс . Вам нужна помощь алгебры? Мы знаем, как ответить: «ГДЗ по алгебре 10 класс» – оптимальное решение для школьников, их . . 

ГДЗ по алгебре . 7 класс 8 класс 9 класс 10 класс 11 класс .  ГДЗ по алгебре — это что вы найдете здесь . Если Вы здесь именно за этим — тогда добро пожаловать .  Ни кто не заставляет 100% и постоянно переписывать с ГДЗ по алгебре, но признайтесь бывают моменты когда . . 

Алгебра 10 класс . Контрольные работы .  Внимательный подход к каждой теме должен помочь школьникам уяснить суть изучаемого материала, но в качестве подсобного средства всегда можно воспользоваться ГДЗ по алгебре 10 класс, который очень прост в использовании . 

ГДЗ для 10 класса по предмету «Алгебра » . Многие школьники считают, что знание алгебры не пригодится им в дальнейшей жизни, ведь все эти формулы мало где можно применить . Однако даже работа программиста требует определенного понимания алгебраических уравнений, не . . 

Используя готовые домашние задания по алгебре для 10 класса , ученик сможет зосто решить любой пример не только из учебника, но и аналогичный из учительского сборника . В решебе по алгебре каждое задание разобрано до мельчайших деталей, что позволяет . . 

Готовые домашние задания по алгебре — 7 класс — Сапожников А .А . — к учебнику Алгебра 7 класс — Алимов Ш .А .  ГДЗ по алгебре для 9 класса 2009 к «Алгебра : учебник для 9 класса общеобразовательных учреждений, Макарычев Ю .Н ., Миндюк Н .Г ., Нешков К .И ., Суворова . . 

Готовые домашние задания .  Учебники по алгебре 10 класс скачать в pdf бесплатно . 

Алгебра – очень нелегкий предмет, именно поэтому, практически каждому ученику просто необходим помощник . Имея три главы с уникальными решениями задач, ГДЗ стали незаменимым атрибутом учеников . Каждый раздел рассматривает свой спектр вопросов . . 

ГДЗ По Английскому 6 Класс Лапа
Решебник По Русскому Языку 10 Класс Гольцова
ГДЗ По Алгебре И Начала Анализа Алимов
ГДЗ По Окружающему Проект
ГДЗ Калинина 1 Класс По Учебнику
ГДЗ По Географии 9 Класс Учебник
ГДЗ По Русскому 7 Класс Рыбченкова Фгос
ГДЗ Матем Мордкович
ГДЗ Меркин 5 Класс
ГДЗ Математика Контрольное Измерительное 4 Класса
ГДЗ Английский 1 Спотлайт
ГДЗ По Английскому Языку Старлайт 8 Класс
ГДЗ Русский Язык Страница 100
ГДЗ Сборник Заданий 6 Класс
ГДЗ 4 Класс Математика Карточки
ГДЗ Решебник По Алгебре 8 Класс
ГДЗ По Математике 1 Класс Учебник Чекин
ГДЗ По Истории Мира 5 Класс
ГДЗ По Русскому Языку Второй Класс Климанова
ГДЗ Ефросинина Рабочая Тетрадь 2 Часть
ГДЗ 1 Класс Самостоятельные Работы Математика Петерсон
ГДЗ Алгебра 7 Колягин Ткачева Шабунин
Решебник По Математике 5 Класса Герасима
ГДЗ Англ 7 Класс Афанасьева Михеева Учебник
ГДЗ Английский 9 Афанасьева 2 Часть
Решебник По Физике 11 Класс Мякишев
ГДЗ По Английскому 7 Класс Подоляко Учебник
ГДЗ По Геометрии 7 Класс Мордкович Учебник
ГДЗ Математика Бантова Третий Класс
Загладин Белоусов Всеобщая История 10 Класс ГДЗ
ГДЗ По Алгебре 7 Класс Номер 934
Математика 2 Учебник Ответы Решебник
ГДЗ По Геометрии 7 Класс Тематические
ГДЗ По Физике 11 Й Класс Мякишев
ГДЗ По Русскому Класс Часть
Angl Gdz Ru ГДЗ Spotlight
ГДЗ История 11 Левандовский
ГДЗ Петерсон 7
ГДЗ Окружающий Рабочая Тетрадь Третий Класс
Решебник Ваулина Рабочая Тетрадь
ГДЗ По Алгебре Решение
Решебник По Математике 5 Петерсон 2
Решебник По Русской Мове 7 Класс
Решебник Поляковой 3 2 Часть
Канакина 2 Учебник Решебник
ГДЗ Годер 5 Класса Часть 2
ГДЗ По Алгебре 7 Класс Мерзляк 2020
ГДЗ По Алгебре 9 Класс Гольдман
ГДЗ По Русскому Учебник Пименова
ГДЗ По Английскому Языку 7 Юнит

Гдз По Русскому 9 Класс Ладыженский

Дронов Класс ГДЗ 9 Класс

ГДЗ По Русскому Языку 7 Класс Ладышкина

ГДЗ Английский 10 Класс По Страницам

Гдз По Математике 1 Класс Истомин

вопросы и ответы – Рамблер/класс

17317 вопросов

17497 ответов

21.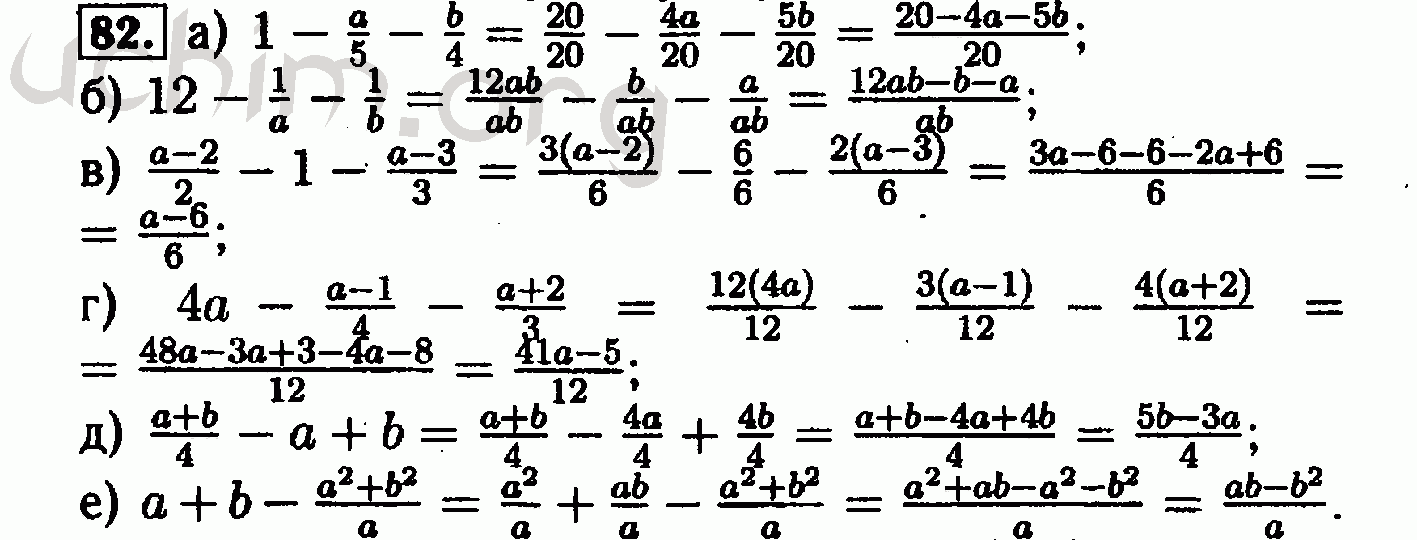 22 Постройте график функции. С помощью графика найдите… Алгебра Мордкович 8 класс

21.22 Постройте график функции у = 5 — | х + 2|. С помощью графика найдите:
а)    наибольшее значение функции;
б)    (Подробнее…)

ГДЗМордкович А.Г.Алгебра8 класс

Мордкович алгебра 8 класс 33.26. При каких значениях переменной произведение выражений…

33.26.
а) При каких значениях переменной произведение выражений 3x + 8 и x + 12 больше утроенного квадрата второго (Подробнее…)

ГДЗ8 классАлгебраМордкович А.Г.

Мордкович алгебра 8 класс 20.27. Используя график функции, найдите…

(Подробнее…)

ГДЗМордкович А.Г.Алгебра8 класс

Найти длину промежутка неравенства. Задание 92 Алгебра 9 класс Мордкович А.Г.

Как найти длину промежутка неравенства?
Найдите длину промежутка, являющегося решением неравенства -5 ≤ 2х + 11 ≤ 1. (Подробнее.. .)

ГДЗАлгебраМордкович А.Г.9 класс

Представить в виде корня из степени с целым показателем. Алгебра. 9 класс. Алимов Ш. А. Параграф 10. Упражнение №119.

Привет) Скоро контрольная…помогите подготовится пожалуйста 😉 (Подробнее…)

ГДЗАлгебраАлимов Ш.А.Школа9 класс

Хело! Помогите решить! № 6.19 Алгебра 9 класс Мордкович

Решите систему уравнений:
  (Подробнее…)

ГДЗАлгебра9 классМордкович А.Г.

Помогите вычислить. Алгебра. 8 класс. Пар.№23. Упр.№341. Учебник Алимов Ш.А.

Здравствуйте! Помогите вычислить: (Подробнее…)

ГДЗ8 классАлгебраАлимов Ш.А.

Привет! Поможете мне построить график? № 47.9 ГДЗ Алгебра 10-11 класс Мордкович.

Постройте график  функции:
а) у = ех+4;                                                            
б) у = е-х + 1; (Подробнее…)

ГДЗАлгебра10 класс11 классМордкович А. Г.

Определим четверть…Упр 424 параграф 22 Алимов Алгебра 10-11 класс

Кто поможет? Буду благодарна!
Определить четверть, в которой расположена точка, полученная поворотом точки Р (1; 0) на (Подробнее…)

ГДЗ10 классАлимов Ш.А.Алгебра

Привет! Помогите найти точку. № 32.31 ГДЗ Алгебра 10-11 класс Мордкович.

На графике функции у = √x; найдите точку М, ближай­шую к точке А (4,5; 0).

ГДЗАлгебра10 класс11 классМордкович А.Г.

Алимов гдз алгебра гдз 494

Привет. кто сталкивался с задачкой 494? скинете решение ?
    Выяснить, какие из точек А (1; 3), В (1; 2), С (0; 1),
В (-1; (Подробнее…)

АлгебраАлимов Ш.А.ГДЗ9 класс

Алгебра Оценить длину средней линии треугольника 931 8 класс Макарычев

Подскажите как решить
Оцените длину средней линии треугольника АВС, которая параллельна стороне АВ, если 10,4 < АВ <10,5. (Подробнее…)

АлгебраМакарычев Ю.Н.8 классГДЗДомашнее задание

Помогите мне найти значение многочлена: 241 Алгебра Алимов 7 класс

Найти значение многочлена:
1) -0,08x + 73ху3 + 27ху2 при х = 4 и y = 0,2;
 

АлгебраАлимов Ш.А.7 классГДЗ

Помогите с неравенствами. Алгебра. 8 класс. Пар.№10. Упр.№166. Учебник Алимов Ш.А.

Здравствуйте! Вот условие: (Подробнее…)

ГДЗ8 классАлгебраАлимов Ш.А.

Оценить длину трапеции Алгебра 8 класс Макарычев Задача

Привет, подскажите как ответить
Оцените длину средней линии трапеции с основаниями а см и с см, если  3,4  ≤  а ≤  3,5  и    6,2 ≤ (Подробнее…)

Алгебра8 классМакарычев Ю.Н.ГДЗ

Приветик! Поможете с решением? № 30.30 ГДЗ Алгебра 10-11 класс Мордкович.

Найдите точки экстремума заданной функции и определите  их  характер: (Подробнее…)

ГДЗАлгебра10 класс11 классМордкович А. Г.

Алгебра 8 класс Макарычев 943 Наименьшие и наибольшие числа

Привет. Поделитесь решением задачи
Принадлежит ли промежутку [8; 41) число 40,9? Можно ли указать число, большее чем 40,9, (Подробнее…)

Макарычев Ю.Н.Алгебра8 классДомашнее заданиеГДЗ

449 Алгебра 9 класс Макарычев Помогите мне и найдите координаты точек пересечения

Не выполняя построения, найдите координаты точек пересечения:
а)   окружности х2 + у2 = 36 и параболы у = х2 + 6;
б)   (Подробнее…)

АлгебраМакарычев Ю.Н.9 классГДЗ

Привет всем! Кто решал №16.17 алгебра 7 класс Мордкович? Есть у вас гдз?

16.17.      Используя таблицу степеней простых однозначных чисел,
найдите m, если:
а)    2m = 512; б) 5m = 625; в) 1m = 343; (Подробнее…)

ГДЗАлгебра7 классМордкович А.Г.

Мордкович алгебра 8 класс 14.32 найдите приближенное значение выражения

(Подробнее. ..)

ГДЗМордкович А.Г.Алгебра8 класс

похожие темы

ЕГЭ

10 класс

9 класс

11 класс

Количественная геометрия — ПМК

1. Громов М. (1981) Группы полиномиального роста и расширяющиеся отображения. Inst Hautes Études Sci Publ Math 53:53–73.

2. Громов М. (1993) Асимптотические инварианты бесконечных групп. Геометрическая теория групп, Том 2, Сассекс, 1991 , London Math Soc Lecture Note Ser (Cambridge University Press, Кембридж, Великобритания), том 182, стр. 1–295.

3. Брейяр Э., Ле Донн Э. О скорости сходимости к асимптотическому конусу для нильпотентных групп и субфинслеровой геометрии. Proc Natl Acad Sci USA. 2012;110(48):19220–19226. [Google Scholar]

4. Абрамс А., Брэди Н., Дэни П., Янг Р. Гомологическая и гомотопическая функции Дена различны. Proc Natl Acad Sci USA. 2013;110(48):19206–19212. [Google Scholar]

5. Ю.Г. Грубая гипотеза Баума-Конна для пространств, допускающих равномерное вложение в гильбертово пространство. Изобретите математику. 2000;139(1):201–240. [Google Scholar]

6. де Корнюлье Ю., Тессера Р., Валетт А. Изометрические групповые действия на гильбертовых пространствах: рост коциклов. Geom Funct Anal. 2007; 17(3):770–79.2. [Google Scholar]

7. Матушек Ю. О вложении деревьев в равномерно выпуклые банаховы пространства. Израиль Дж. Матем. 1999; 114: 221–237. [Google Scholar]

8. Остин Т., Наор А., Тессера Р. Точная количественная невложимость группы Гейзенберга в суперрефлексивные банаховы пространства. Группы Геом Дин. 2013;7(3):497–522. [Google Scholar]

9. Чигер Дж., Кляйнер Б., Наор А. Границы сжатия для липшицевых отображений из группы Гейзенберга в L 1. Acta Math. 2011;207(2):291–373. [Google Scholar]

10. Гентнер Э., Каминкер Дж. Точность и равномерная вложимость дискретных групп. J Lond Math Soc. 2004;70(3):703–718. [Google Scholar]

11. Громов М. Количественная теория гомотопий. В: Росси Х, редактор. Перспективы в математике: приглашенные беседы по случаю 250-летия Принстонского университета. Род-Айленд: Американское математическое общество, Провиденс; 1999. С. 45–49. [Google Scholar]

12. Ферри С., Вайнбергер С. Количественная алгебраическая топология и гомотопия Липшица. Proc Natl Acad Sci USA. 2013;110(48):19246–19250. [Google Scholar]

13. Колдинг Т.Х., Миникоцци В.П. Монотонность и ее аналитические и геометрические следствия. Proc Natl Acad Sci USA. 2012;110(48):19233–19236. [Google Scholar]

14. Фреше М. Сборник монографий по теории функций. Том 12. Париж: Готье-Вилларс; 1928. Les Espaces Abstraits et leur Théorie Considérée Comme Introduction à l’Analyse Générale. Французский. [Google Scholar]

15. Банах С. Моногра Математика. Том 1. Варшава: PWN — Польское научное издательство; 1932. Теория линейных операций. [Google Scholar]

16. Кадец М.И. Доказательство топологической эквивалентности всех сепарабельных бесконечномерных банаховых пространств. Функциональный . Анальный приложен. 1967; 1: 61–70. [Google Scholar]

17. Рибе М. О равномерно гомеоморфных нормированных пространствах. Ковчег мат. 1976;14(2):237–244. [Google Scholar]

18. Мильман В.Д., Шехтман Г. Конспект лекций по математике. Том 1200. Берлин: Springer; 1986. Асимптотическая теория конечномерных нормированных пространств. [Академия Google]

19. Писье Г. Кембриджские трактаты по математике. Том 94. Кембридж, Великобритания: Cambridge Univ Press; 1989. Объем выпуклых тел и геометрия банахова пространства. [Google Scholar]

20. Дадуш Д., Вемпала С.С. Близкие к оптимальным детерминированные алгоритмы вычисления объема с помощью М-эллипсоидов. Proc Natl Acad Sci USA. 2013;110(48):19237–19245. [Google Scholar]

21. Джонсон В. Б., Одзава Н., Шехтман Г. Количественная версия теоремы о коммутаторе для матриц с нулевым следом. Proc Natl Acad Sci USA. 2012;110(48):19251–19255. [Google Scholar]

22. Бургейн Дж. Метрическая интерпретация сверхрефлексивности в банаховых пространствах. Израиль Дж. Матем. 1986;56(2):222–230. [Google Scholar]

23. Ball K (2012) Программа Ribe. Семинар Бурбаки, разоблачение 1047 .

24. Наор А. Введение в программу Рибе. Японская математика. 2012;7(2):167–233. [Google Scholar]

25. Мендель М., Наор А. Ультраметрические скелеты. Proc Natl Acad Sci USA. 2012;110(48):19256–19262. [Академия Google]

26. Хот С. Труды тридцать четвертого ежегодного симпозиума ACM по теории вычислений. Нью-Йорк: ACM; 2002. О мощности уникальных 2-доказательных 1-раундовых игр; стр. 767–775. [Google Scholar]

27. Хот С (2010) Неаппроксимируемость NP-полных задач, дискретный анализ Фурье и геометрия. Труды Международного конгресса математиков (Индостанское книжное агентство, Нью-Дели), том 4, стр. 2676–2697.

28. Ловаш Л. О шенноновской емкости графа.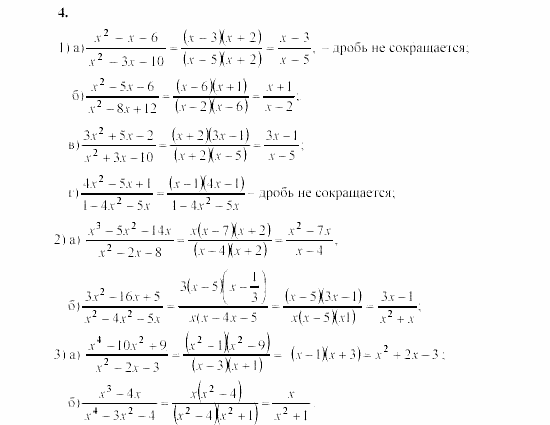 IEEE Trans Inf Theory. 1979;25(1):1–7. [Google Scholar]

29. Алон Н., Макарычев К., Макарычев Ю., Наор А. Квадратичные формы на графах. Изобретите математику. 2006;163(3):499–522. [Google Scholar]

30. Briet J, Burman H, Gijswijt D. Нарушение шенноновской емкости метрических графов с запутанностью. Proc Natl Acad Sci USA. 2012;110(48):19227–19232. [Бесплатная статья PMC] [PubMed] [Google Scholar]

31. Барак Б., Двир З., Вигдерсон А., Йегудаёв А. Дробные теоремы Сильвестра–Галлаи. Proc Natl Acad Sci USA. 2012;110(48):19213–19219. [Google Scholar]

32. Ай А., Двир З., Сараф С., Вигдерсон А. (2012) Теоремы типа Сильвестра-Галлаи для приближенной коллинеарности. архив: 1211.0331v1.

33. Пансу П. Круассан де буль и геодезических ферм данс ле nilvariétés. Эргодическая теория динамических систем. 1983;3(3):415–445. [Google Scholar]

34. Grötschel M, Lovász L, Schrijver A. Алгоритмы и комбинаторика. 2-е изд. Том 2. Берлин: Springer; 1993. Геометрические алгоритмы и комбинаторная оптимизация. [Академия Google]

35. Барани И., Фюреди З. Аппроксимация сферы многогранниками с малым числом вершин. Proc Am Math Soc. 1988;102(3):651–659. [Google Scholar]

36. Мильман В.Д. Inégalité de Brunn-Minkowski inverse и приложения à la théorie locale des espaces normés. C R Acad Sci, Ser 1 Math. 1986;302(1):25–28. [Google Scholar]

37. Бургейн Дж., Цафрири Л. Об одной проблеме Кадисона и Зингера. J Reine Angew Math. 1991; 420:1–43. [Google Scholar]

38. Маркус А., Спилман Д.А., Сривастава Н. (2013) Переплетающиеся семейства II: смешанные характеристические полиномы и проблема Кадисона-Зингера. архив: 1306.3969в3.

39. Талагранд М. Закономерность гауссовских процессов. Акта Математика. 1987; 159 (1-2): 99–149. [Google Scholar]

40. Келети Т., Мате А., Зиндулка О. (2012) Хаусдорфова размерность метрических пространств и липшицевы отображения на кубы. архив: 1203.0686v2.

41. Бартал Ю., Линиал Н., Мендель М., Наор А. О метрических явлениях типа Рамсея. Энн Мат. 2005;162(2):643–709. [Google Scholar]

42. Бартал Ю., Боллобас Б., Мендель М. Теоремы типа Рамсея для метрических пространств с приложениями к онлайн-задачам. J Comput Syst Sci. 2006;72(5):890–921. [Google Scholar]

43. Мендель М., Наор А. Рэмси Разделы и структуры данных близости. J Eur Math Soc. 2007;9(2):253–275. [Google Scholar]

44. Чечик С. (2013) Оракул приблизительного расстояния с постоянным временем запроса. архив: 1305.3314v1.

45. Дворецкий А. Труды Международного симпозиума по линейным пространствам, Иерусалим, 1960. Иерусалим: Иерусалимское академическое издательство; 1961. Некоторые результаты о выпуклых телах и банаховых пространствах; стр. 123–160. [Академия Google]

46. Bourgain J, Figiel T, Milman V. О гильбертовых подмножествах конечных метрических пространств. Израиль Дж. Матем. 1986;55(2):147–152. [Google Scholar]

47. Мендель М., Наор А. Ультраметрические подмножества с большой хаусдорфовой размерностью. Изобретите математику. 2013;192(1):1–54. [Google Scholar]

48. Мильман В.Д. Почти евклидовы факторпространства подпространств конечномерного нормированного пространства. Proc Am Math Soc. 1985; 94(3):445–449. [Google Scholar]

49. Мендель М., Наор А. Евклидовы частные конечных метрических пространств. Adv Math 189(2):451–494. 2004 [Google Scholar]

50. Мильман В.Д. Явления, происходящие в высоких измерениях. Успехи мат наук. 2004;59(1):157–168. [Google Scholar]

Семинар Дагштуля 18231: Проблема удовлетворения ограничений: сложность и аппроксимация

Задача об удовлетворении ограничений , или сокращенно CSP, обеспечивает унифицирующую структуру, в которой можно естественным образом выразить широкий спектр вычислительных задач, связанных с отображениями и назначениями, включая выполнимость, раскрашиваемость графов и системы вычислений. уравнения. Фреймворк CSP возник 30-35 лет назад независимо в искусственном интеллекте, теории баз данных и теории графов под тремя разными обличьями и был реализован только в конце 19 века. 90-х, что на самом деле это разные грани одной и той же фундаментальной проблемы. В настоящее время CSP широко используется в теоретической информатике, будучи математическим объектом с очень богатой структурой, который обеспечивает отличную лабораторию как для методов классификации, так и для алгоритмических методов; в то время как в ИИ и более прикладных областях информатики эта структура широко рассматривается как универсальный и эффективный способ моделирования и решения множества реальных проблем, таких как планирование и составление графиков, проверка программного обеспечения и понимание естественного языка, чтобы назвать немного. Экземпляр CSP состоит из набора переменных, набора значений для переменные и набор ограничений, которые ограничивают комбинации значений которые могут принимать определенные подмножества переменных. Учитывая такой случай, возможный вопросы включают в себя (а) принятие решения о том, имеет ли место присвоение значений переменные, чтобы выполнялись все ограничения, или оптимизация таких назначений различными способами, или (б) найти задание, удовлетворяющее как можно большему числу ограничений.

возможный. Существует множество важных модификаций и расширений этого базового рамок, например, те, которые имеют дело с заданиями на подсчет или включают в себя программные или глобальные ограничения.

Удовлетворение ограничений всегда играло центральную роль в вычислительной технике. теория сложности; соответствующие версии CSP являются классическими полными проблемами для большинства стандартных классов сложности. CSP представляют собой очень богатую и в то же время достаточно управляемый класс проблем, чтобы дать хорошее представление об общем вычислительные явления. Например, они помогают понять, какие математические свойства делают вычислительную задачу разрешимой (в широком смысле, например, разрешимой за полиномиальное время, нетривиально аппроксимируемой, разрешимой с фиксированными параметрами или определимой в слабой логике). Одной из самых поразительных особенностей этого направления исследований является разнообразие различных разделов математики (включая универсальную алгебру и логику, комбинаторику и теорию графов, теорию вероятностей и математическое программирование), которые используются для достижения глубокого понимания при изучении CSP.

В последнее десятилетие исследовательская деятельность в этой области значительно активизировалась и был достигнут впечатляющий прогресс.

Свидетелями недавнего всплеска активности по теме семинара являются четыре предыдущие семинары Dagstuhl под названием «Сложность ограничений» (06401) и «CSP: сложность и аппроксимируемость» (09441, 12541, 15301), которые были состоявшихся в 2006, 2009, 2012 и 2015 годах соответственно. Этот семинар стал продолжением семинаров 2009, 2012 и 2015 годов. Действительно, обмен идеями на семинарах 2009, 2012 и 2015 годов привел к новым амбициозным исследовательским проектам и налаживание регулярных каналов связи. Очевидно, что есть потенциал для дальнейшее систематическое взаимодействие, которое будет продолжать обогащать области и открытие новых направлений исследований. Семинар 2018 года собрал 47 исследователи из различных высокоразвитых областей удовлетворения ограничений и привлекло много специалистов, использующих универсальные алгебраические, комбинаторные, геометрические и вероятностные методы для изучения алгоритмических задач, связанных с CSP.

Участники представили в 24 докладах свои последние результаты по ряду важных вопросов, касающихся темы семинара. Одной из особенностей этого семинара является значительное увеличение количества докладов, затрагивающих несколько подобластей и подходов в рамках его исследовательского направления, что является явным признаком растущей синергии, которая является одной из основных целей этой серии семинаров.

Заключительные замечания и планы на будущее: Семинар был хорошо принят, о чем свидетельствует высокий уровень принятых приглашения и высокая степень вовлеченности участников. Из-за множество впечатляющих результатов, о которых было сообщено в ходе семинара, и активная дискуссии между исследователями разных областей знаний, организаторами считают этот семинар большим успехом. С постоянно растущим взаимодействием между такими исследователями, мы предвидим еще один семинар, посвященный взаимодействию между различными подходами к изучению сложности и аппроксимируемости CSP.

В завершение организаторы хотели бы выразить благодарность Научным руководителям Дагштульского центра за поддержку семинара.

Описание тем семинара

Классическая вычислительная сложность CSP. Несмотря на доказуемое существование промежуточных задач (скажем, между P и NP-полными, если предположить, что P = / NP), исследования вычислительной сложности привели к широко известному неформальному тезису о том, что «естественные задачи почти всегда полны для стандартных классов сложности». CSP активно использовались для поддержки и уточнения этого тезиса. Точнее, несколько ограниченных форм CSP были подробно исследованы. Одним из основных видов ограничений является

ограничение языка ограничение, т.е. ограничение на доступные типы ограничений. Выбрав подходящий язык ограничений, можно решить многие известные вычислительные задачи из теории графов, логики и алгебры. Изучение ограничения языка ограничений было основано на CSP Дихотомическая гипотеза Федера и Варди, в которой говорится, что для каждого фиксированного языка ограничений соответствующий CSP является либо P-, либо NP-полным. Существуют аналогичные предположения о дихотомии в отношении других классов сложности (например, L и NL). Недавние прорывы в сложности CSP стали возможными благодаря введению универсально-алгебраического подхода, который извлекает алгебраическую структуру из языка ограничений. и использует его для анализа проблемных экземпляров. Вышеупомянутые гипотезы имеют алгебраические версии, которые также предсказывают в алгебраических терминах, где граница между более сложные проблемы и более легкие проблемы лежат. Алгебраический подход применялся для доказательства гипотезы о дихотомии во многих важных частных случаях (например, теоремы Булатова о дихотомии для трехзначных и консервативных CSP), кульминацией которого стали два независимых доказательства общей гипотезы, озвученной в 2017 году Булатовым и Жуком.

• Булатов и Жук подробно рассказали об основных моментах своих доказательств.
• Колмогоров описал алгоритм для булевых CSP с тем ограничением, что каждая переменная появляется ровно в двух ограничениях, и все ограничения являются даже дельта-матроидами.

Ценная CSP (VCSP) представляет собой значительное обобщение CSP, которое включает в себя как осуществимость, аспекты оптимизации. В то время как вычислительная сложность конечной области VCSP к настоящему времени хорошо изучены, VCSP с бесконечной областью достаточно хорошо изучены. неизведанный.

• Виола выступил с докладом о субмодульных VCSP на бесконечных доменах.
• Казда представил свои результаты по структуре взвешенных клонов, которые тесно связано с вычислительной сложностью VCSP.

Аппроксимируемость CSP. Использование алгоритмов аппроксимации один из самых плодотворных подходов к преодолению NP-трудности. Однако сложные проблемы оптимизации демонстрируют различное поведение. относительно аппроксимируемости, что делает его захватывающей областью исследований, которая к настоящему времени хорошо развиты, но далеки от полного понимания.

Новая тема, объединяющая сложность CSP с аспектами аппроксимации является удовлетворение ограничения обещания (PCSP).

PCSP — это обобщение CSP, в котором ограничения представлены парами «более строгие» и «более слабые» версии. В экземпляре PCSP задача состоит в том, чтобы найти назначение, удовлетворяющее более слабым ограничениям, при обещании, что существует назначение, удовлетворяющее строгим ограничениям.

• Бракензик выступил с вводной речью об этом захватывающем направлении исследований, а также представил дихотомическую классификацию симметричных логических PCSP.
• Опрсал объяснил совсем недавно введенный алгебраический подход к вычислительная сложность PCSP.
• Барто представил свои результаты по PCSP и циклическим операциям.

Многие алгоритмы приближения для CSP основаны на выпуклых релаксациях.

• Беркхольц сделал обзор релаксаций для булевых CSP на основе алгебраических методы.
• Шрамм объяснил силу релаксаций полуопределенного программирования для случайных CSP.
• Тулсиани представил результаты о пределах ослаблений линейного программирования для CSP.
• Макарычев показал, как получить разрыв целочисленности для линейной функции Калинеску-Карлоффа-Рабани. программная релаксация проблемы Multiway-Cut.
• Острин установил самый известный в настоящее время результат неприближения для Мин. UnCut, который представляет собой специальный логический CSP.

Некоторые из самых захватывающих достижений в области аппроксимации за последнее десятилетие вращаться вокруг гипотеза уникальных игр , или UGC, из Khot (2002). Эта смелая гипотеза утверждает, что для CSP с определенным языком ограничений в достаточно большой области NP-сложно отличить почти выполнимые экземпляры от тех, в которых может быть удовлетворена лишь небольшая часть ограничений. Известно, что эта гипотеза влечет за собой точные результаты о неаппроксимируемости для многих классических задач оптимизации. Более того, если UGC верен, то, как показал Рагхавендра в 2008 г., простой алгоритм, основанный на полуопределенном программирование обеспечивает наилучшее возможное приближение для

все CSP (хотя точное качество этого приближения неизвестно).

• Мошковиц представил последние разработки по так называемой теореме PCP 2-to-2, которая охватывает важные частные случаи UGC.

Логика и сложность CSP. Логика использовалась двумя разными способами при изучении CSP. Один из них, начиная с более ранней работы Колайтиса и Варди, — это дескриптивная сложность , где CSP пытаются классифицировать как классы экземпляров в отношении определимости в данной логике. Другой способ — использовать логику для указания экземпляров CSP, что можно сделать очень естественным образом. Последнее направление ведет к таким обобщениям, как квантовая CSP (QCSP), а также к изучению CSP над бесконечными областями, где были обнаружены важные связи с алгебраическим подходом.

• Рой представил теорему дихотомии для обратной задачи выполнимости.
• Бодирский рассказал о двух методах сведения CSP с бесконечной областью к конечнодоменные CSP.
• Пинскер объяснил недавние результаты алгебраического подхода к бесконечной области CSP. Эти результаты связаны с так называемыми петлевыми условиями, которые более подробно обсуждались Козиком.
• Компачер представил доказательство эквивалентности двух гипотез о дихотомии. для CSP с бесконечным доменом.
• Мотте представил новое доказательство дихотомии MMSNP и обсудил последствия для CSP с бесконечным доменом.
• Мартин описал недавние результаты для временных и пространственных задач, которые частные случаи CSP с бесконечной областью.

Точная экспоненциальная сложность CSP. Область параметризованной сложности тесно связана с областью точной экспоненциальная сложность, в которой цель состоит в том, чтобы разработать наиболее эффективный алгоритмы экспоненциального времени. Был достигнут значительный прогресс в точном экспоненциальная сложность CSP.

• Головнев представил результаты, дающие оптимальные нижние оценки времени работы алгоритмы определения наличия гомоморфизма одного графа на другой.

  No related posts.