Разработка урока по физике по теме «Определение жесткости пружины»
Конспект урока по физике
Лабораторная работа
«Определение жесткости пружины» и
«Определение коэффициента трения скольжения»
Учебник «Физика 10 класс» авторы Л.Э. Генденштейн, Ю.И. Дик
Разработала:
Васильева Д.Н. учитель физики высшей квалификационной категории
Цель урока: в ходе проведения лабораторного практикума выработать общий подход к изучению сил электромагнитной природы, на примере силы трения и силы упругости.
Задачи урока:
Показать межпредметную связь физики и математики при обобщении результатов лабораторного исследования.
Отработка навыков работы с физическими приборами.

Вовлекать учащихся в активную творческую деятельность, воспитывать культуру общения на уроке и при изложении собственных мыслей.
Применяемые технологии: технология ИКТ
Применяемые формы работы: групповая работа в парах, работа с виртуальной лабораторией и реальным оборудованием.
На столах перед учениками: листочки с планом выполнения лабораторной работы, рисунком и расчётной таблицей, индивидуальным заданием, а так же — оборудование для определения жесткости пружины, ноутбук с установленной виртуальной лабораторной работой «Определение коэффициента трения скольжения»
На демонстрационном столе: деревянная линейка, деревянный брусок, набор грузиков, динамометр, штатив.
На доске: название лабораторных работ, координатные оси, для построения графиков при обсуждении результатов исследования, домашнее задание.
Ход урока:
Организационный момент.(1 минута)
Здравствуйте, ребята! Мне очень приятно видеть вас готовыми к уроку. Очень рассчитываю на нашу совместную плодотворную работу. Сегодня мы с вами продолжим исследование двух важнейших сил в природе — силы трения и силы упругости. Выступая в роли исследователей, попробуем определить, в чем сходство в этих на первый взгляд таких не похожих друг на друга силах и попытаемся в процессе исследования выработать общий подход к изучению подобных сил.
Фронтальный опрос.(5 минут)
| 1Когда возникает сила упругости? 2)Какие виды деформации вы знаете? 3)В чем заключается природа силы упругости? 4)От чего зависит величина силы упругости? 5)Что такое коэффициент упругости? |
Подготовка к выполнению работы.
 (2 минуты)
(2 минуты)
Провожу демонстрацию, перемещая брусок с грузом по поверхности деревянной линейки. Заостряю внимание на сложность равномерного перемещения двух трущихся поверхностей относительно друг друга и на колебания стрелки динамометра. Для исследования силы трения будем использовать виртуальную лабораторию (ноутбуки). Компьютер упрощает измерения. Нам лишь останется обработать результаты, полученные в виртуальном эксперименте. Также демонстрирую один из опытов второй лабораторной работы.
Одним из результатов исследования является определение коэффициента трения и коэффициента упругости по полученным в ходе работы зависимостям.
Для этого обращаю внимание ребят на распечатки, в которых описана лабораторная работа. Чтоб получить оценку «хорошо» — предстоит выполнить все задания из уровня «А» и если претендуете на более высокую оценку «отлично», то и уровень «В» также должен быть выполнен безошибочно. На каждую работу отводится 15 минут.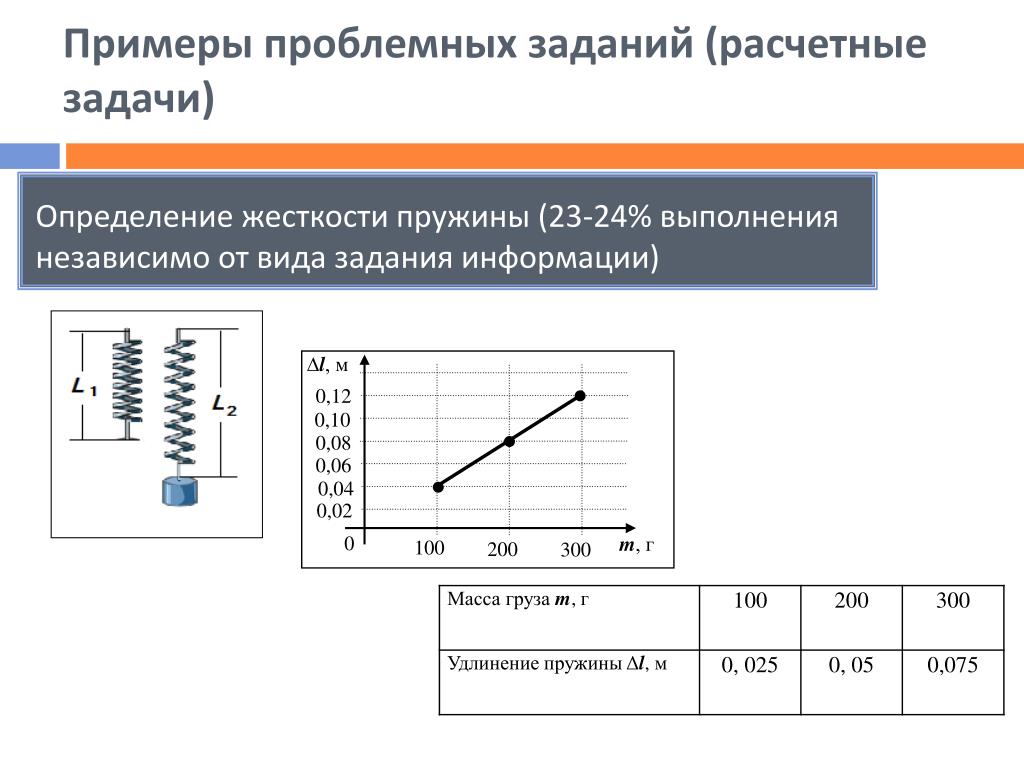 В ходе урока ученики меняются местами с ребятами, выполняющими другое исследование. Таким образом, через 30 минут мы сможем подвести итоги работы.
В ходе урока ученики меняются местами с ребятами, выполняющими другое исследование. Таким образом, через 30 минут мы сможем подвести итоги работы.
Выполнение лабораторной работы.(30 минут)
В течение 15 минут учащиеся выполняют одну лабораторную работу. Из каждой группы учеников к доске вызывается 1 человек для построения полученной зависимости. И ученики, меняясь местами, заканчивают выполнение второй работы.
Анализ результатов выполненной работы.(5минут)
В конце урока на доске находятся 2 графика с помощью которых ученики определяли коэффициенты. Проговорим еще раз последовательность действий нахождения каждого из них. И обсудим следующие вопросы:
Как построить график по экспериментальным точкам?
Что такое аппроксимация?
Чему равен тангенс угла наклона графика? (При обсуждении этого вопроса на доске цветным мелом дорисовывается прямоугольный треугольник, из которого видно, что и .
)
Формулируем вывод о том, каков общий подход к изучению сил имеющих аналогичные зависимости.
В заключение урока(2 минуты).
Я благодарю вас за плодотворную работу! Мне хотелось бы узнать: с каким оборудованием вам было работать легче, интересней, результативней? Достигли ли мы поставленной цели?
Прошу записать Д/З: Тех, кто хотел бы повысить свою оценку может в домашней тетради провести расчет погрешностей экспериментов. Для всех остальных § 21 (Пункт1. Опр. наизусть)
Выходя из кабинета тетрадочки с лабораторными работами мне положить на край кафедры.
Спасибо за урок! До свиданья!
Приложения
Лабораторная работа №3
Определение жесткости пружины.
Цель работы: проверить справедливость закона Гука для пружины динамометра и измерить коэффициент жесткости этой пружины.
Оборудование: штатив с муфтой и зажимом, динамометр с заклеенной шкалой, набор грузов известной массы (по 100 г), линейка с миллиметровыми делениями.
Описание работы: Согласно закону Гука, модуль F силы упругости и модуль х. удлинения пружины связаны соотношением F=кх. Измерив F и х, можно найти коэффициент жесткости к по формуле к= F/х.
Ход работы:
Уровень «А»
Закрепите динамометр в штативе на достаточно большой высоте.
Подвешивая различное число грузов (от 1-го до 4-х), вычислите для каждого случая соответствующее значение F=mg, а также измерьте соответствующее удлинение пружины х.
Результаты измерений и вычислений запишите в таблицу:
№ опыта
m, кг
mg, H
х, м
1
0,1
2
0,2
3
0,3
4
0,4
Начертите оси координат x и F, выберите удобный масштаб и нанесите полученные экспериментальные точки.

Оцените (качественно) справедливость закона Гука для данной пружины: находятся ли экспериментальные точки вблизи одной прямой, проходящей через начало координат.
Запишите сделанный вами вывод.
Вычислите коэффициент жесткости по формуле: k =F/х , используя результаты опыта №4 это обеспечит наибольшую точность.
Уровень «В»
8.Для вычисления погрешности надо использовать опыт №4, потому что ему соответствует наименьшая относительная погрешность измерения. Вычислите границы Fmin и Fmax , в которых находится истинное значение F , считая, что Fmin = F — ∆F, Fmax = F + ∆F. Примите ∆F = 4 ∆mg, где ∆m — погрешность при изготовлении грузов (для оценки можно считать, что ∆m= 0,005 кг).
xmin = x — ∆x, xmax = x + ∆x, где ∆x = 0,5мм,
Найденные величины запишите в приведенную ниже таблицу.
9.Пользуясь методом оценки погрешности косвенных измерений, найдите
kmax = Fmax/хmin , kmin = Fmin/хmax .
10. Найдите среднее значение kср и абсолютную погрешность измерения ∆ k по формулам
kср = (kmax + kmin) / 2, ∆k
11. Определите относительную погрешность измерения
Определите относительную погрешность измерения
Fmin, H | Fmax, H | xmin, м | xmax,м | kmin,Н/м | kmax,Н/м | kср,Н/м | ∆k,Н/м | ξk |
12. Запишите результат в виде k = kcр ± ∆к , подставив в эту формулу численные значения найденных величин:
13. Запишите вывод: что вы измеряли и какой получен результат.
Лабораторная работа №4
Определение коэффициента трения скольжения.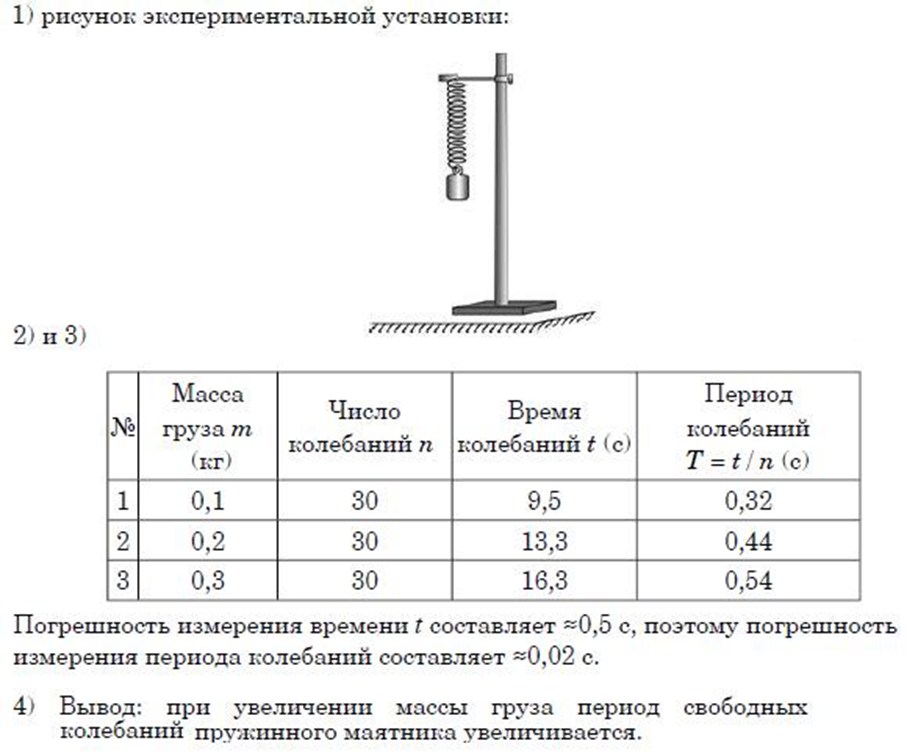
Цель работы: измерить коэффициент трения скольжения дерева по дереву.
Оборудование: деревянный брусок, деревянная линейка, набор грузов известной массы (по 100 г), динамометр.
Описание работы: Если тянуть брусок с грузом по горизонтальной поверхности так, чтобы брусок двигался равномерно, прикладываемая к бруску горизонтальная сила равна по модулю силе трения скольжения, действующей на брусок со стороны поверхности. Модуль силы трения Fтр связан модулем силы нормального давления N соотношением Fтр= μN . Измерив Fтр и N, можно найти коэффициент трения по формуле . В данном случае сила нормального давления N равна весу P бруска с грузом.
Ход работы:
Уровень «А»
Определите с помощью динамометра вес бруска Pбр и запишите в приведенную ниже таблицу.

Положите брусок на горизонтально расположенную деревянную линейку. На брусок поставьте груз.
Поставив на брусок один груз, тяните брусок равномерно по горизонтальной линейке, измеряя с помощью динамометра прикладываемую силу. Повторите опыт, поставив на брусок 2 и 3 груза. Записывайте каждый раз в таблицу значения силы трения Fтр и силы нормального давления N =Pбр+Ргр.
№ опыта
Pбр, H
N, H
Fтр ,Н
1
2
3
Начертите оси координат N и Fтр, выберите удобный масштаб и нанесите полученные три экспериментальные точки.

Оцените (качественно), подтверждается ли на опыте, что сила трения прямо пропорциональна силе нормального давления: находятся ли все экспериментальные точки вблизи одной прямой, проходящей через начало координат.
Запишите сделанный вами вывод.
Вычислите коэффициент трения по формуле , используя результаты опыта №3 (это обеспечивает наибольшую точность).
Уровень «В»
Для вычисления погрешности надо использовать опыт №3, потому что ему соответствует наименьшая относительная погрешность измерения. Вычислите границы Fmin и Fmax, в которых находится истинное значение F, считая, что Fmin=F-∆F, Fmax=F+∆F. С учетом того, что указатель динамометра при движении колеблется, можно принять ∆F=0,1Н.

Найдите границы Nmin и Nmax , в которых находится истинное значение N ,считая что N min =N — ∆N, Nmax= N + ∆N. Примите ∆N=3∆mg+∆Pбр, где ∆m – погрешность при изготовлении грузов (для оценки можно считать, что ∆m =0,005 кг, ∆Pбр=0,05H).
Пользуясь методом оценки погрешности косвенных измерений, найдите
,
Найдите среднее значение μср и абсолютную погрешность ∆μ по формулам:
,
Определите относительную погрешность измерения
Результаты вычислений запишите в таблицу:
Fmin, H
Fmax, H
Nmin, H
Nmax, H
μmin
μmax
μср
∆μ
ξμ
Запишите результат в виде μ = μср ± ∆μ, подставив в эту формулу численные значения найденных величин.

Запишите вывод: что вы измеряли и какой получен результат.
Лабораторная работа номер 3 определение жесткости пружины. Лабораторная работа «определение жесткости пружины»
Лабораторная работа №
Измерение жесткости пружины
10 класс
Цель работы: найти жесткость пружины из измерений
удлинения пружины при различных
значениях силы тяжести
,
уравновешивающей силу упругости
,
на основе закона Гука:
.
Приборы и материалы:
В каждом из опытов жесткость
определяется при разных значениях силы
упругости и удлинения, т.е.
условия опыта меняются. Поэтому для
нахождения среднего значения жесткости
нельзя вычислить среднее арифметическое
результатов измерений. Воспользуемся
графическим способом нахождения
среднего значения, который может быть
применен в таких случаях. По результатам
нескольких опытов построим график
зависимости модуля силы упругости
от
модуля удлинения х. При построении
графика по результатам опыта
экспериментальные точки могут не
оказаться на прямой, которая соответствует
формуле
По результатам
нескольких опытов построим график
зависимости модуля силы упругости
от
модуля удлинения х. При построении
графика по результатам опыта
экспериментальные точки могут не
оказаться на прямой, которая соответствует
формуле
. Это связано с погрешностями
измерения: В этом случае график надо
проводить так, чтобы примерно одинаковое
число точек оказалось по разные стороны
от прямой. После построения графика
возьмите точку на прямой (в средней
части графика), определите по нему
соответствующие этой точке значения
силы упругости и удлинения и вычислите
жесткость k.
Она и будет искомым средним значением
жесткости пружины
.
Результат измерения обычно
записывается в виде выражения
,
где
— наибольшая абсолютная
погрешность измерения. Известно, что
относительная погрешность ()
разна отношению абсолютной погрешности к значению
величины k:
,
откуда
.
В данной работе
.
Поэтому
,
где
,
,
Абсолютные погрешности:
= 0,002 кг;
=1мм,
.
Порядок выполнения работы
Закрепите на штативе конец спиральной пружины.
Рядом с пружиной или за ней установите и закрепите линейку с миллиметровыми делениями.
Отметьте и запишите то деление линейки, против которого приходится стрелка-указатель пружины.
Подвесьте к пружине груз известной массы и измерьте вызванное им удлинение пружины.
К первому грузу добавьте второй, третий и т.д. грузы, записывая каждый раз удлинение х пружины. По результатам измерений заполните таблицу:
По
физике
за 9 класс (И.К.Кикоин, А.К.Кикоин, 1999 год),
задача №2
к главе «ЛАБОРАТОРНЫЕ РАБОТЫ ».
Цель работы: найти жесткость пружины из измерений удлинения пружины при различных значениях силы тяжести
уравновешивающей силу упругости на основе закона Гука:
В каждом из опытов жесткость определяется при разных значениях силы упругости и удлинения, т. е. условия опыта меняются. Поэтому для нахождения среднего значения жесткости нельзя вычислить среднее арифметическое результатов измерений. Воспользуемся графическим способом нахождения среднего значения, который может быть применен в таких случаях. По результатам нескольких опытов построим график зависимости модуля силы упругости F упр от модуля удлинения |x|. При построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле
Воспользуемся графическим способом нахождения среднего значения, который может быть применен в таких случаях. По результатам нескольких опытов построим график зависимости модуля силы упругости F упр от модуля удлинения |x|. При построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле
Это связано с погрешностями измерения. В этом случае график надо проводить так, чтобы примерно одинаковое число точек оказалось по разные стороны от прямой. После построения графика возьмите точку на прямой (в средней части графика), определите по нему соответствующие этой точке значения силы упругости и удлинения и вычислите жесткость k. Она и будет искомым средним значением жесткости пружины k ср.
Результат измерения обычно записывается в виде выражения k = = k cp ±Δk, где Δk — наибольшая абсолютная погрешность измерения. Из курса алгебры (VII класс) известно, что относительная погрешность (ε k) равна отношению абсолютной погрешности Δk к значению величины k:
откуда Δk — ε k k.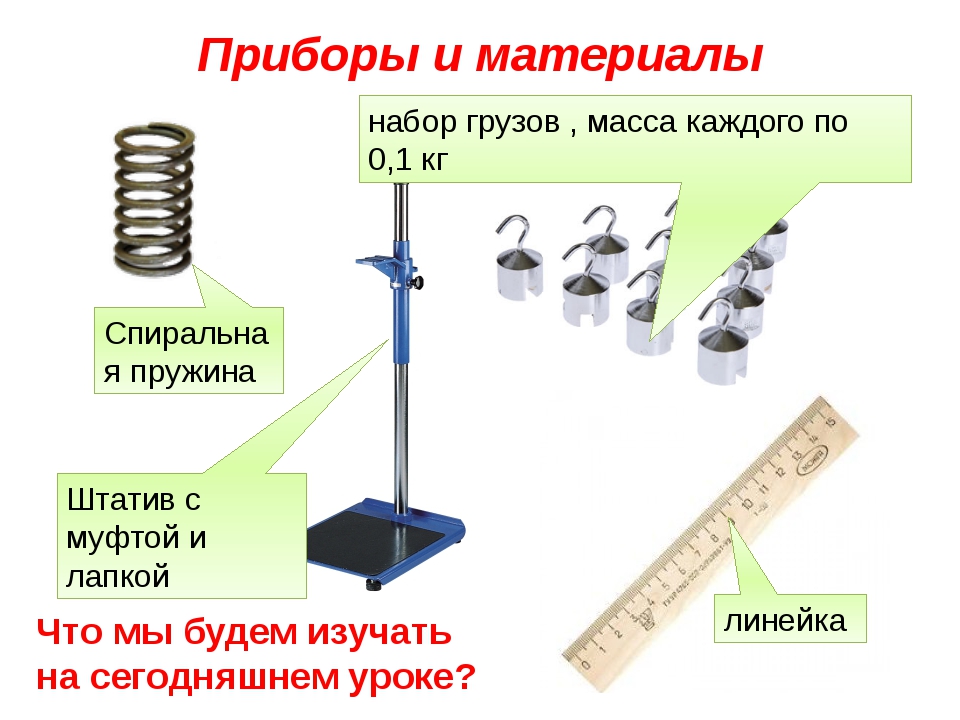 Существует правило для расчета относительной погрешности: если определяемая в опыте величина находится в результате умножения и деления приближенных величин, входящих в расчетную формулу, то относительные погрешности складываются. В данной работе
Существует правило для расчета относительной погрешности: если определяемая в опыте величина находится в результате умножения и деления приближенных величин, входящих в расчетную формулу, то относительные погрешности складываются. В данной работе
Средства измерения: 1) набор грузов, масса каждого равна m 0 = 0,100 кг, а погрешность Δm 0 = 0,002 кг; 2) линейка с миллиметровыми делениями.
Материалы: 1) штатив с муфтами и лапкой; 2) спиральная пружина.
Порядок выполнения работы
1. Закрепите на штативе конец спиральной пружины (другой конец пружины снабжен стрелкой-указате-лем и крючком — рис. 176).
2. Рядом с пружиной или за ней установите и закрепите линейку с миллиметровыми делениями.
3. Отметьте и запишите то деление линейки, против которого приходится стрелка-указатель пружины.
4. Подвесьте к пружине груз известной массы и измерьте вызванное им удлинение пружины.
5. К первому грузу добавьте второй, третий и т. д. грузы, записывая каждый раз удлинение |х| пружины. По результатам измерений заполните таблицу:
По результатам измерений заполните таблицу:
6. По результатам измерений постройте график зависимости силы упругости от удлинения и, пользуясь им, определите среднее значение жесткости пружины k cp .
7. Рассчитайте наибольшую относительную погрешность, с которой найдено значение k ср (из опыта с одним грузом). В формуле (1)
так как погрешность при измерении удлинения Δx=1 мм, то
8. Найдите
и запишите ответ в виде:
1 Принять g≈10 м/с 2 .
Закон Гука: «Сила упругости, возникающая при деформации тела, пропорциональна его удлинению и направлена противоположно направлению перемещения частиц тела при деформации».
Закон Гука
Жесткостью называют коэффициент пропорциональности между силой упругости и изменением длины пружины под действием приложенной к ней силы. Согласно третьему закону Ньютона, приложенная к пружине сила по модулю равна возникшей в ней силе упругости. Таким образом жесткость пружины можно выразить как:
где F — приложенная к пружине сила, а х — изменение длины пружины под ее действием. Средства измерения: набор грузов, масса каждого равна m 0 = (0,1±0,002) кг.
Средства измерения: набор грузов, масса каждого равна m 0 = (0,1±0,002) кг.
Линейка с миллиметровыми делениями (Δх = ±0,5 мм). Порядок выполнения работы описан в учебнике и комментариев не требует.
масса, кг | удлинение |х|, | |||
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Лабораторная работа «Измерение жесткости пружины» Учитель физики ГБОУ СОШ №145 Калининского района Санкт- Петербурга Карабашьян М.В.
проверить справедливость закона Гука для пружины динамометра и измерить коэффициент жесткости этой пружины. Цель работы Оборудование: набор «Механика» из комплекта L-micro- штатив с муфтой и зажимом, динамометр с заклеенной шкалой, набор грузов известной массы (по 50 г), линейка с миллиметровыми делениями.
Подготовительные вопросы Что такое сила упругости? Как вычислить силу упругости, возникающую в пружине при подвешивании к ней груза массой m кг? Что такое удлинение тела? Как измерить удлинение пружины при подвешивании к ней груза? В чем заключается закон Гука?
Правила техники безопасности Будьте осторожны при работе с растянутой пружиной. Не роняйте и не бросайте грузы.
Описание работы: Согласно закону Гука, модуль F силы упругости и модуль х удлинения пружины связаны соотношением F = kx . Измерив F и х, можно найти коэффициент жесткости k по формуле
В каждом из опытов жесткость определяется при разных значениях силы упругости и удлинения, т. е. условия опыта меняются. Поэтому для нахождения среднего значения жесткости нельзя вычислить среднее арифметическое результатов измерений. Воспользуемся графическим способом нахождения среднего значения, который может быть применен в таких случаях. По результатам нескольких опытов построим график зависимости модуля силы упругости F упр от модуля удлинения \ х\ . При построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле F yпp =k\x\ . Это связано с погрешностями измерений. В этом случае график надо проводить так, чтобы примерно одинаковое число точек, оказалось, по разные стороны от прямой. После построения графика возьмите точку на прямой (в средней части графика) определите по нему соответствующие этой точке значения силы упругости и удлинения, и вычислите жесткость k . Она и будет искомым средним значением жесткости пружины k ср.
При построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле F yпp =k\x\ . Это связано с погрешностями измерений. В этом случае график надо проводить так, чтобы примерно одинаковое число точек, оказалось, по разные стороны от прямой. После построения графика возьмите точку на прямой (в средней части графика) определите по нему соответствующие этой точке значения силы упругости и удлинения, и вычислите жесткость k . Она и будет искомым средним значением жесткости пружины k ср.
1. Закрепите на штативе конец спиральной пружины (другой конец пружины снабжен стрелкой-указателем и крючком). 2. Рядом с пружиной или за ней установите и закрепите линейку с миллиметровыми делениями. 3. Отметьте и запишите то деление линейки, против которого приходится стрелка-указатель пружины. 4. Подвесьте к пружине груз известной массы и измерьте вызванное им удлинение пружины. 5. К первому грузу добавьте второй, третий и т. д. грузы, записывая каждый раз удлинение \ х\ пружины. По результатам измерений заполните таблицу ХОД РАБОТЫ:
По результатам измерений заполните таблицу ХОД РАБОТЫ:
№ опыта m, кг mg, H х, м 1 0,1 2 0,2 3 0,3 4 0,4
6. Начертите оси координат х и F, выберите удобный масштаб и нанесите полученные экспериментальные точки. 7. Оцените (качественно) справедливость закона Гука для данной пружины: находятся ли экспериментальные точки вблизи одной прямой, проходящей через начало координат. 8. По результатам измерений постройте график зависимости силы упругости от удлинения и, пользуясь им, определите среднее значение жесткости пружины k ср. 9. Рассчитайте наибольшую относительную погрешность, с которой найдено значение k cp 10. Запишите сделанный вами вывод.
Контрольные вопросы: Как называется зависимость между силой упругости и удлинением пружины? Пружина динамометра под действием силы 4Н удлинилась на 5 мм. Определите вес груза, под действием которого эта пружина удлиняется на 16 мм.
Решение задачи:
цель работы: найти жесткость пружины из измерений удлинения пружины при различных значениях силы тяжести
уравновешивающей силу упругости на основе закона гука:
в каждом из опытов жесткость определяется при разных значениях силы упругости и удлинения, т. е. условия опыта меняются. поэтому для нахождения среднего значения жесткости нельзя вычислить среднее арифметическое результатов измерений. воспользуемся графическим способом нахождения среднего значения, который может быть применен в таких случаях. по результатам нескольких опытов построим график зависимости модуля силы упругости f упр от модуля удлинения |x|. при построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле
е. условия опыта меняются. поэтому для нахождения среднего значения жесткости нельзя вычислить среднее арифметическое результатов измерений. воспользуемся графическим способом нахождения среднего значения, который может быть применен в таких случаях. по результатам нескольких опытов построим график зависимости модуля силы упругости f упр от модуля удлинения |x|. при построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле
это связано с погрешностями измерения. в этом случае график надо проводить так, чтобы примерно одинаковое число точек оказалось по разные стороны от прямой. после построения графика возьмите точку на прямой (в средней части графика), определите по нему соответствующие этой точке значения силы упругости и удлинения и вычислите жесткость k. она и будет искомым средним значением жесткости пружины k ср.
результат измерения обычно записывается в виде выражения k = = k cp ±δk, где δk — наибольшая абсолютная погрешность измерения. из курса алгебры (vii класс) известно, что относительная погрешность (ε k) равна отношению абсолютной погрешности δk к значению величины k:
из курса алгебры (vii класс) известно, что относительная погрешность (ε k) равна отношению абсолютной погрешности δk к значению величины k:
откуда δk — ε k k. существует правило для расчета относительной погрешности: если определяемая в опыте величина находится в результате умножения и деления приближенных величин, входящих в расчетную формулу, то относительные погрешности складываются. в данной работе
поэтому
средства измерения: 1) набор грузов, масса каждого равна m 0 = 0,100 кг, а погрешность δm 0 = 0,002 кг; 2) линейка с миллиметровыми делениями.
материалы: 1) штатив с муфтами и лапкой; 2) спиральная пружина.
порядок выполнения работы
1. закрепите на штативе конец спиральной пружины (другой конец пружины снабжен стрелкой-указате-лем и крючком — рис. 176).
2. рядом с пружиной или за ней установите и закрепите линейку с миллиметровыми делениями.
3. отметьте и запишите то деление линейки, против которого приходится стрелка-указатель пружины.
4. подвесьте к пружине груз известной массы и измерьте вызванное им удлинение пружины.
5. к первому грузу добавьте второй, третий и т. д. грузы, записывая каждый раз удлинение |х| пружины. по результатам измерений заполните таблицу:
номер опыта | m, кг | mg 1 , н | |х|, м |
6. по результатам измерений постройте график зависимости силы упругости от удлинения и, пользуясь им, определите среднее значение жесткости пружины k cp .
7. рассчитайте наибольшую относительную погрешность, с которой найдено значение k ср (из опыта с одним грузом). в формуле (1)
так как погрешность при измерении удлинения δx=1 мм, то
8. найдите
и запишите ответ в виде:
1 принять g≈10 м/с 2 .
закон гука: «сила упругости, возникающая при деформации тела, пропорциональна его удлинению и направлена противоположно направлению перемещения частиц тела при деформации».
закон гука
жесткостью называют коэффициент пропорциональности между силой упругости и изменением длины пружины под действием приложенной к ней силы. согласно третьему закону ньютона, приложенная к пружине сила по модулю равна возникшей в ней силе упругости. таким образом жесткость пружины можно выразить как:
где f — приложенная к пружине сила, а х — изменение длины пружины под ее действием. средства измерения: набор грузов, масса каждого равна m 0 = (0,1±0,002) кг.
линейка с миллиметровыми делениями (δх = ±0,5 мм). порядок выполнения работы описан в учебнике и комментариев не требует.
№ опыта | масса, кг | удлинение |х|, | к, н/м | |
м |
Лабораторная работа «Измерение жёсткости пружины»
Цель работы: найти жёсткость пружины из измерений пружины при различных значениях
силы тяжести Fт, уравновешивающей силу упругости Fупр, на основании закона Гука k= Fупр/х. В
каждом из опытов жёсткость определяется при разных значениях силы упругости и удлинения,
т.е. условия опыта меняются. Поэтому для нахождения среднего значения нельзя вычислить
среднее арифметическое результатов измерений. По результатам нескольких опытов построим
график зависимости Fупр от удлинения х. При построении графика по результатам опыта
экспериментальные точки могут оказаться не на одной прямой, которая определяется
соответственно формуле Fупр=kx. Это связано с погрешностями измерения. В этом случае
график нужно проводить так, чтобы примерно одинаковое число точек оказалось по разные
стороны от прямой. После построения графика возьмите точку на прямой (в средней части
графика), определите по нему соответствующие этой точке значения силы упругости и
удлинения и вычислите жёсткость k. Она и будет искомым средним значением жёсткости
пружины kср.
Результат измерения записывается в виде выражения k=kср±Δk, где Δk – абсолютная
k
погрешность измерения. Относительная погрешность εk=
, откуда Δk=εkk.
В
каждом из опытов жёсткость определяется при разных значениях силы упругости и удлинения,
т.е. условия опыта меняются. Поэтому для нахождения среднего значения нельзя вычислить
среднее арифметическое результатов измерений. По результатам нескольких опытов построим
график зависимости Fупр от удлинения х. При построении графика по результатам опыта
экспериментальные точки могут оказаться не на одной прямой, которая определяется
соответственно формуле Fупр=kx. Это связано с погрешностями измерения. В этом случае
график нужно проводить так, чтобы примерно одинаковое число точек оказалось по разные
стороны от прямой. После построения графика возьмите точку на прямой (в средней части
графика), определите по нему соответствующие этой точке значения силы упругости и
удлинения и вычислите жёсткость k. Она и будет искомым средним значением жёсткости
пружины kср.
Результат измерения записывается в виде выражения k=kср±Δk, где Δk – абсолютная
k
погрешность измерения. Относительная погрешность εk=
, откуда Δk=εkk.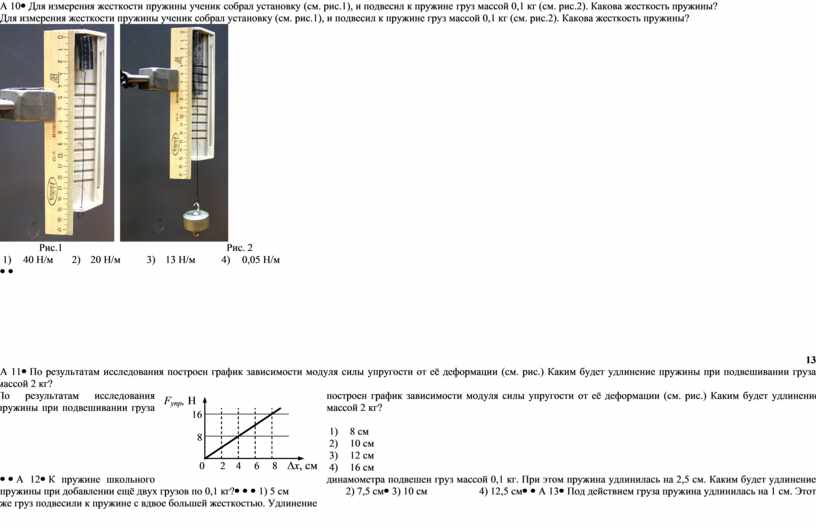 Существует
k
правило для расчёта относительной погрешности: если определяемая в опыте величина
находится в результате умножения и деления приближённых величин, входящих в расчётную
формулу, то относительные погрешности складываются. В данной работе
k= Fупр/х. Поэтому εk=εF+εx.
Приборы и материалы: 1) Набор грузов, штатив с муфтой и лапкой, динамометр, линейка с
миллиметровыми делениями.
Порядок выполнения работы.
1. Закрепите в штативе динамометр.
2. Рядом закрепите или установите линейку с миллиметровыми делениями.
3. Подвесьте к пружине груз, измерьте возникшую силу упругости и удлинение пружины.
4. Добавьте второй, третий и т.д. грузы и повторите измерения. По результатам измерений
заполните таблицу.
Номер опыта
1
2
3
4
F, Н
х, м
5. По результатам измерений постройте график зависимости силы упругости от удлинения
пружины и, пользуясь им, определите среднее значение жёсткости пружины kср.
6. Рассчитайте относительную погрешность, с которой найдено kср (из опыта с одним
F
x
грузом).
Существует
k
правило для расчёта относительной погрешности: если определяемая в опыте величина
находится в результате умножения и деления приближённых величин, входящих в расчётную
формулу, то относительные погрешности складываются. В данной работе
k= Fупр/х. Поэтому εk=εF+εx.
Приборы и материалы: 1) Набор грузов, штатив с муфтой и лапкой, динамометр, линейка с
миллиметровыми делениями.
Порядок выполнения работы.
1. Закрепите в штативе динамометр.
2. Рядом закрепите или установите линейку с миллиметровыми делениями.
3. Подвесьте к пружине груз, измерьте возникшую силу упругости и удлинение пружины.
4. Добавьте второй, третий и т.д. грузы и повторите измерения. По результатам измерений
заполните таблицу.
Номер опыта
1
2
3
4
F, Н
х, м
5. По результатам измерений постройте график зависимости силы упругости от удлинения
пружины и, пользуясь им, определите среднее значение жёсткости пружины kср.
6. Рассчитайте относительную погрешность, с которой найдено kср (из опыта с одним
F
x
грузом). В опыте εF=
, εx=
. Погрешность при измерении удлинения Δx=1 мм,
F
x
погрешность при измерении силы ΔF=0,1Н.
7. Найдите Δk=εkkср и в выводе запишите ответ в виде k=kср±Δk.
Лабораторная работа «Измерение коэффициента трения»
Цель работы: Определить коэффициент трения деревянного бруска, скользящего по
поверхности, использую формулу Fтр=μP. С помощью динамометра измеряют силу, с которой
нужно равномерно тянуть брусок с грузами по горизонтальной поверхности. Эта сила равна по
модулю силе трения Fтр. С помощью того же динамометра можно найти вес бруска с грузом.
Определив таким образом значения силы трения при различных значениях веса тела,
необходимо построить график зависимости Fтр от Р и найти среднее значение коэффициента
трения, как в предыдущей работе.
Приборы и материалы: деревянный брусок, поверхность (например, парты), набор грузов,
динамометр.
Порядок выполнения работы.
1. Положите брусок на горизонтальную поверхность.
2. Прикрепите к бруску динамометр, равномерно тяните его по поверхности, заметив при
этом показания динамометра.
В опыте εF=
, εx=
. Погрешность при измерении удлинения Δx=1 мм,
F
x
погрешность при измерении силы ΔF=0,1Н.
7. Найдите Δk=εkkср и в выводе запишите ответ в виде k=kср±Δk.
Лабораторная работа «Измерение коэффициента трения»
Цель работы: Определить коэффициент трения деревянного бруска, скользящего по
поверхности, использую формулу Fтр=μP. С помощью динамометра измеряют силу, с которой
нужно равномерно тянуть брусок с грузами по горизонтальной поверхности. Эта сила равна по
модулю силе трения Fтр. С помощью того же динамометра можно найти вес бруска с грузом.
Определив таким образом значения силы трения при различных значениях веса тела,
необходимо построить график зависимости Fтр от Р и найти среднее значение коэффициента
трения, как в предыдущей работе.
Приборы и материалы: деревянный брусок, поверхность (например, парты), набор грузов,
динамометр.
Порядок выполнения работы.
1. Положите брусок на горизонтальную поверхность.
2. Прикрепите к бруску динамометр, равномерно тяните его по поверхности, заметив при
этом показания динамометра. 3. Взвесьте брусок и груз.
4. К первому грузу добавьте второй, третий грузы, каждый раз взвешивая брусок и грузы и
измеряя силу трения. Результаты измерений занесите в таблицу
Номер опыта
1
2
3
4
Р, Н
ΔР, Н
Fтр, Н
ΔFтр, Н
5. По результатам измерений постройте график зависимости Fтр от Р и найти среднее
значение коэффициента трения μср.
6. Рассчитайте относительную погрешность измерения коэффициента трения. Т.к. μ= Fтр/Р,
то ε μ=εFтр+εР. С наибольшей погрешностью измерен коэффициент трения в опыте с
одним грузом. Найдите абсолютную погрешность Δ μ= ε μ μср и запишите в выводе ответ
в виде μ= μ ср±Δ μ.
3. Взвесьте брусок и груз.
4. К первому грузу добавьте второй, третий грузы, каждый раз взвешивая брусок и грузы и
измеряя силу трения. Результаты измерений занесите в таблицу
Номер опыта
1
2
3
4
Р, Н
ΔР, Н
Fтр, Н
ΔFтр, Н
5. По результатам измерений постройте график зависимости Fтр от Р и найти среднее
значение коэффициента трения μср.
6. Рассчитайте относительную погрешность измерения коэффициента трения. Т.к. μ= Fтр/Р,
то ε μ=εFтр+εР. С наибольшей погрешностью измерен коэффициент трения в опыте с
одним грузом. Найдите абсолютную погрешность Δ μ= ε μ μср и запишите в выводе ответ
в виде μ= μ ср±Δ μ.
Измерение жесткости пружины — Документ
Лабораторная работа №
Измерение жесткости пружины
10 класс
Цель работы: найти жесткость пружины из измерений
удлинения пружины при различных
значениях силы тяжести
,
уравновешивающей силу упругости
,
на основе закона Гука:
.
Приборы и материалы:
штатив с муфтой и лапкой,
спиральная пружина,
набор грузов, масса каждого равна =0,100 кг,
линейка с миллиметровыми делениями.
В каждом из опытов жесткость
определяется при разных значениях силы
упругости и удлинения, т.е.
условия опыта меняются. Поэтому для
нахождения среднего значения жесткости
нельзя вычислить среднее арифметическое
результатов измерений. Воспользуемся
графическим способом нахождения
среднего значения, который может быть
применен в таких случаях. По результатам
нескольких опытов построим график
зависимости модуля силы упругости
от
модуля удлинения х. При построении
графика по результатам опыта
экспериментальные точки могут не
оказаться на прямой, которая соответствует
формуле. Это связано с погрешностями
измерения: В этом случае график надо
проводить так, чтобы примерно одинаковое
число точек оказалось по разные стороны
от прямой. После построения графика
возьмите точку на прямой (в средней
части графика), определите по нему
соответствующие этой точке значения
силы упругости и удлинения и вычислите
жесткость k.
Она и будет искомым средним значением
жесткости пружины
.
После построения графика
возьмите точку на прямой (в средней
части графика), определите по нему
соответствующие этой точке значения
силы упругости и удлинения и вычислите
жесткость k.
Она и будет искомым средним значением
жесткости пружины
.
Результат измерения обычно записывается в виде выражения , где — наибольшая абсолютная погрешность измерения. Известно, что относительная погрешность () разна отношению абсолютной погрешности к значению величины k:
, откуда .
В данной работе . Поэтому , где , ,
Абсолютные погрешности:
= 0,002 кг;
=1мм,
.
Порядок выполнения работы
Закрепите на штативе конец спиральной пружины.
Рядом с пружиной или за ней установите и закрепите линейку с миллиметровыми делениями.

Отметьте и запишите то деление линейки, против которого приходится стрелка-указатель пружины.
Подвесьте к пружине груз известной массы и измерьте вызванное им удлинение пружины.
К первому грузу добавьте второй, третий и т.д. грузы, записывая каждый раз удлинение х пружины. По результатам измерений заполните таблицу:
Номер опыта | m, кг | mg, Н | Fупр, Н | x, м |
По результатам измерений постройте график зависимости силы упругости от удлинения и, пользуясь им, определите среднее значение жесткости пружины .

Рассчитайте наибольшую относительную погрешность, с которой найдено значение(из опыта с одним грузом).
Найдите и запишите ответ в виде:
Лабораторная работа «Определение жёсткости пружины»
Тип ПОЛабораторная работа PASCOActivInspire (Promethean)SMART NotebookПрезентация PowerPointAнимационный Flash-роликУрок для ActivTableElite Panaboard (Panaboard)HitachiМастер-классMimioStudio™RM Easiteach Next Generation (TriumphBoard, Panaboard, Legamaster)Interwrite WorkSpace (Interwrite)IP board (IPBoard /Julong)Интересный материал
ПредметМузыкаФранцузский языкАстрономияИнформатикаГеографияОкружающий мирБиологияНемецкий языкОбщественные наукиМатематикаТатарский языкОРКСЭкономикаИностранный языкМХКВоспитательная работа (классный час)Русский языкОБЖГеометрияАнглийский языкТехнологияПриродоведениеОбществознаниеВнеурочное занятиеЕстественные наукиФизикаХимияЛитератураИсторияПравоИЗОЧерчениеДругое
Уровень образованияДошкольное образованиеНачальная школаСредняя школаСтаршая школаВысшая школаСредне-специальное образованиеСреднее образованиеПрофессиональное образованиеСпециальное образованиеДистанционное обучениеВнеурочные занятияДополнительное образование
Вид урокаМетодические рекомендацииРазработка урокаИграФрагмент урокаВнеурочные занятияДидактический материалШаблонСценарий
Классдошкольное1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 классне зависит от класса
Рекомендованные
Сбросить фильтрИНДИВИДУАЛЬНЫЙ ИТОГОВЫЙ ПРОЕКТ НА ТЕМУ «Измерение Коэффициента жёсткости пружины.
 Закон Гука»
Закон Гука»МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №2»
МУНИЦИПАЛЬНОГО ОБРАЗОВАНИЯ ГОРОДСКОЙ ОКРУГ СИМФЕРОПОЛЬ
РЕСПУБЛИКИ КРЫМ
ИНДИВИДУАЛЬНЫЙ ИТОГОВЫЙ ПРОЕКТ
НА ТЕМУ
«Измерение Коэффициента жёсткости пружины. Закон Гука»
Выполнил:
Гальченко Денис
ученик 9-А класса
Руководитель проекта:
Байкова Рамиля Мукаддасовна
учитель физики
Симферополь, 2020 год
Паспорт проекта
Название проекта:«Измерение жёсткости пружины. Закон Гука»
Руководитель:учитель физики Байкова Рамиля Мукаддасовна
Автор: Гальченко Денис ученик 9-А класса
Учебная дисциплина: физика
Тип проекта:исследовательский
Цель работы: определить коэффициентжёсткость пружины из измерений удлинения пружины при различных значениях силы тяжести.
Задачи работы:
1. Изучить научную информацию о процессе деформации твердых тел и описать в окружающем мире явления, которые могут быть объяснены с помощью закона Гука.
2. Определить способ, оборудование и процедуру для экспериментальной проверки закона Гука.
3. Измерить опытным путем коэффициент жёсткости пружины из измерений удлинения пружины при различных значениях силы тяжести и проверить закон Гука.
4. Сформулировать выводы.
Вопрос проекта: как опытным путем определить коэффициент жёсткости пружины из измерений удлинения пружины при различных значениях силы тяжести?
Краткое содержание: в работе даны теоретические определенияпроцесса деформации физических тел, закона Гука, рассмотрены примеры проявления данного процесса в окружающем мире. Проведено экспериментальное исследование, в котором с целью проверки закона Гука мы подвергли небольшой деформации пружину, меняя вес, подвешенных к ней грузов. На основании полученных измерений и, используя закон Гука, был рассчитан коэффициент жёсткости пружины и построен график зависимости растяжения пружины от изменения нагрузки, оказанной на неё. Таким образом, был определенкоэффициентжёсткости пружины из измерений удлинения пружины при различных значениях силы тяжести.
Результатом проекта является видеоролик, в котором наглядно представлены сбор экспериментальной установки, поэтапная процедура проведения эксперимента, математический расчет коэффициента жёсткости пружины и графическое изображение зависимости силы упругости от удлинения.
Пояснительная записка
Автор: Гальченко Денис ученик 9-А класса
Тема:«Измерение жёсткости пружины. Закон Гука»
Цель: определить коэффициентжёсткость пружины из измерений удлинения пружины при различных значениях силы тяжести.
Основополагающий вопрос:как опытным путем, с помощью закона Гука, определить коэффициент жёсткости пружины из измерений удлинения пружины при различных значениях силы тяжести?
Продукт: видеоролик
Этапы работы с проектом:
Этапы | Сроки | Результат |
Определение темы и цели проекта | Конец Сентября | Определение темы проекта |
Встреча с руководителем проекта | Конец Сентября | Получение помощи и направления дальнейших действий |
Составление плана работы | Начало Октября | Определения чёткого плана работы |
Поиск информации | Середина Октября | Расширение знаний по теме проекта |
Проведение эксперимента | Конец февраля | Получение измерений |
Создание продукта | Конец марта | Видеоролик |
Содержание
Введение……………………………………………………………………. | 6 | |
1 | Закона Гука: теоретический и прикладной аспекты………………… | 6 |
1.1 | ОпределениеЗакона Гука ……………………………………………………… | 6 |
1.2 | Проявление Закона Гука в окружающей среде………………………. | 6 |
2 | Опытно-экспериментальная работа по определению коэффициента жёсткости пружины …………………………………………………… | 8 |
2.1 | Планирование экспериментальной работы и техническое обеспечение……………….…………………………………………….. | 8 |
2.2 | Определение коэффициента жёсткости пружины …………………… | 8 |
2.3 | Математические расчёты коэффициента жёсткости пружины …….. | 9 |
Вывод ………………………………………………………………………. | 11 | |
Список литературы …………………………………………………………. | 12 | |
Приложения………………………………………………………………….. | 13 | |
Введение
Физика изучает взаимодействие всех тел, как парадоксально маленьких, так и невероятно больших. Одним из примеров взаимодействия между телами является процесс деформации. Деформация – это изменение формы и размеров тела под действием внешних сил, при изменении температуры, влажности, фазовых превращениях и других воздействиях, вызывающих изменение положения частиц тела.
Процесс деформации был описан в 1660 году известным английским ученым Робертом Гуком. Закон Гука − основной закон теории упругости. Гук проделал множество опытов с разными предметами из самых разных материалов различной геометрической формы. Здесь были и пружины, и куски проволоки, и балки.
Закона Гука: теоретический и прикладной аспекты
ОпределениеЗакон Гука
Закон Гука гласит: сила упругости, возникающая при упругой деформации растяжения или сжатия тела, пропорциональна абсолютному значению изменения длины тела [1, 5].
В виде уравнения закон Гука записывается в следующей форме:
F = –kx,
где F — сила упругого сопротивления струны;
x — линейное растяжение или сжатие;
k — так называемый коэффициент упругости.
Знак минус в формуле указывает на то, что силы упругости противодействуют деформациям.
Проявление Закона Гука в окружающей среде
Закон Гука мы используем каждый день и можем этого не замечать. Еще в неолите, не зная этого закона, наши предки изобрели первое дальнобойное оружие – лук и стрелы, используя упругость изогнутой ветки дерева; потом катапульты и баллисты, построенные для метания больших камней, использовали упругость канатов, свитых из растительных волокон или даже из женских длинных волос [3].
Одним из важных практических применений закона Гука являются пружинные весы. Это прибор, у которого пружина и стрелка, собраны в корпусе, который имеет градуированную шкалу. Эти весы имеют крюк, за который их можно повесить, и еще один крюк, на который помещается тело для взвешивания.
Можно привести ряд примеров применения силы упругости в технике: на ухабах сила упругости амортизатора (рессора) помогает гасить колебания автомобиля; подушка безопасности при авариях гасит силу удара; ремень безопасности имеет большую силу упругости, поэтому крепко держит водителя на сидении при толчках и авариях; зимой шины накачивают не до предела, увеличивают их упругость, во-первых холод сжимает сам эти шины, во- вторых, возникает хорошее сцепление со снегом [2].
Применение одноосного растяжения мы видим и в музыкальных инструментах. Высота звука, издаваемого натянутой струной, зависит от силы ее натяжения. Струнные инструменты создаются путем натяжения струн из жесткого материала, стальной проволоки или сухожилий на подходящую жесткую раму, которой может служить гриф гитары. Незначительно изменяя натяжение струны, мы меняем высоту звука. Именно поэтому такие инструменты очень чувствительны к настройке. Я как человек, играющий на гитаре, сталкиваюсь с использованием данного закона каждый день.
Если внимательно присмотреться, то можно обнаружить, что закон Гука, находит свое выражение во множестве практических действий, например, глядя на удочку, можно определить, поймали вы сома или плотву, даже, убивая муху на стене из рогатки, применяется закон Гука.
Сила упругости проявляется как в мире, созданном человеком, так и в природе: в результате действия силы упругости животные могут выдерживать большие нагрузки. Деревья выдерживают порывы ветра, налипший слой снега.
Как и любая сила, сила упругости, способна совершать работу. Причем очень полезную. Она предохраняет деформируемое тело от разрушения. Если она с этим не справляется, наступает разрушение тела. Например, разрывается трос подъёмного крана, струна на гитаре, резинка на рогатке, пружина на весах, лопается воздушный шарик. Эта работа всегда имеет знак минус, поскольку сама сила упругости тоже отрицательна [4].
Закон, открытый Гуком, до настоящего времени является базисным в сопротивлении материалов и служит математической основой теории упругости.
Опытно-экспериментальная работа по определению коэффициента жёсткости пружины
Планирование экспериментальной работы и техническое обеспечение
С целью проверки закона Гука и измерения коэффициента жёсткости пружины, нами была проведена опытно-экспериментальная работа: определено необходимое оборудование, собрана экспериментальная установка, установлен порядок действий. После проведения опыта сделаны расчёты, в которых определен коэффициент жёсткости пружины с последующим изображением графика зависимости силы упругости от удлинения.
Оборудование: динамометр (приложение 1, рис. 1), грузы (приложение 1, рис. 2), линейка, листик бумаги, штатив с муфтой и лапкой (приложение 1, рис 3).
Определение коэффициента жёсткости пружины
Ход экспериментальной работы:
1. Закрепим на штативе динамометр.
2. Рядом с пружиной расположим листик.
3. Отметьте начальное положение конца пружины.
4. Подвесим к пружине груз известной массы и отметьте удлинение пружины.
5. К первому грузу добавим второй и отметим удлинение пружины.
6. К первому и второму грузу добавим третий и отметим удлинение пружины.
7. Измерим линейкой расстояние между отметками.
8. Результаты запишите в таблицу.
9. Рассчитаем коэффициент жёсткости пружины по формулам.
10. По результатам постройте график зависимости силы упругости от удлинения.
2.3. Математические расчёты коэффициента жёсткости пружины
Нахождение Δx:
Δx=x2-x1
Где Δx –это удлинение пружины
x1- длинна пружины, без груза
x2- длинна растянутой пружины, под весом груза
Изображение удлинения пружины, представлено на рисунке 4.
Рисунок 4. Удлинение пружины
В таблице 1 представлены, расчёты удлинения пружины в 3-ёх опытах, под действием грузов разной массы.
Таблица 1
Расчёт удлинения пружины, в 3-ёх опытах
№ опыта | m (кг) | F тяж (Н) | Δx (m) |
1 | 0. | 1 | 0,022 |
2 | 0.2 | 2 | 0,045 |
3 | 0.3 | 3 | 0,067 |
Расчёт
Fупр=kΔx
P=Fупр
k=Fупр/Δx [H/м]
k1=1/0,022≈45H/м
k2=2/0,045≈44H/м
k3=3/0,067≈45H/м
k ср= 45+44+45/3≈ 44/6 H/м
График зависимости силы упругости от удлинения изображен на рисунке 5.
Рисунок 5. График зависимости силы упругости от удлинения
Ось х – удлинение пружины (Δx)
Осьy – сила упругости (Fупр)
Вывод
В ходе проведения проекта:
— получены навыки сбора, обработки и анализа информации по проблеме деформации твердых тел;
— приобретен опыт планирования и проведения экспериментальной деятельности по изучению природы возникновения силы упругости и закону Гука;
— в соответствии с поставленной целью, в ходе экспериментальной работы определен коэффициент жёсткости пружины из измерений удлинения пружины при различных значениях силы тяжести.
Таким образом, анализ информации и наблюдение позволили увидеть, как математический закон находит свое выражение в явлениях окружающей действительности, а проведенный эксперимент позволил опытным путем подтвердить истинность закона Гука.
Перспективу возможной дальнейшей работы по проблеме данного проекта можно определить в экспериментальном исследовании условий, при которых закон Гука справедлив, а при которых он теряет свою силу, то есть исследование степени применимости данного закона.
Результат работы представлен в форме видеоролика и может носить практическую ценность в качестве наглядного материала для проведения лабораторных и практических занятий по физике.
Список литературы
Громцева О. Физика. 7-9 классы. Справочник. ФГОС.– М.: Экзамен, 2020., 192 с.
Книга для чтения по физике: Учеб. пособие для учащихся 6-7 классов./
сост. И.Г. Кириллова. – М.: Просвещение, 1986., 207 с.
Перельман Я. И. Занимательная физика. В двух книгах. Книга 2. – М.: Римис, 2015., 256 с.
Книга 2. – М.: Римис, 2015., 256 с.
Физика. 7 класс: учебник / А. В. Перышкин. – М.: Дрофа, 2016., 192 с.
Физика 7 класс: учебник / О. Ф. Кабардин. – М.: Просвещение, 2009., 176 с.
Интернет-ресурсы
Сила упругости и закон Гука
https://nzmetallspb.ru/benzoinstrument/koeffitsient-zhestkosti-pruzhiny-opredelenie-formuly-izmerenie.html
Приложение 1
Рисунок 1. Динамометр
Рисунок 2. Грузы
Рисунок 3. Штатив с муфтой и лапкой
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/411316-individualnyj-itogovyj-proekt-na-temu-izmeren
Лабораторная работа измерение жесткости пружины мякишев. Лабораторная работа «определение жесткости пружины». Начертите систему координат для построения графика зависимости силы упругости от удлинения пружины
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts. google.com
google.com
Подписи к слайдам:
Лабораторная работа «Измерение жесткости пружины» Учитель физики ГБОУ СОШ №145 Калининского района Санкт- Петербурга Карабашьян М.В.
проверить справедливость закона Гука для пружины динамометра и измерить коэффициент жесткости этой пружины. Цель работы Оборудование: набор «Механика» из комплекта L-micro- штатив с муфтой и зажимом, динамометр с заклеенной шкалой, набор грузов известной массы (по 50 г), линейка с миллиметровыми делениями.
Подготовительные вопросы Что такое сила упругости? Как вычислить силу упругости, возникающую в пружине при подвешивании к ней груза массой m кг? Что такое удлинение тела? Как измерить удлинение пружины при подвешивании к ней груза? В чем заключается закон Гука?
Правила техники безопасности Будьте осторожны при работе с растянутой пружиной. Не роняйте и не бросайте грузы.
Описание работы: Согласно закону Гука, модуль F силы упругости и модуль х удлинения пружины связаны соотношением F = kx . Измерив F и х, можно найти коэффициент жесткости k по формуле
Измерив F и х, можно найти коэффициент жесткости k по формуле
В каждом из опытов жесткость определяется при разных значениях силы упругости и удлинения, т. е. условия опыта меняются. Поэтому для нахождения среднего значения жесткости нельзя вычислить среднее арифметическое результатов измерений. Воспользуемся графическим способом нахождения среднего значения, который может быть применен в таких случаях. По результатам нескольких опытов построим график зависимости модуля силы упругости F упр от модуля удлинения \ х\ . При построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле F yпp =k\x\ . Это связано с погрешностями измерений. В этом случае график надо проводить так, чтобы примерно одинаковое число точек, оказалось, по разные стороны от прямой. После построения графика возьмите точку на прямой (в средней части графика) определите по нему соответствующие этой точке значения силы упругости и удлинения, и вычислите жесткость k . Она и будет искомым средним значением жесткости пружины k ср.
Она и будет искомым средним значением жесткости пружины k ср.
1. Закрепите на штативе конец спиральной пружины (другой конец пружины снабжен стрелкой-указателем и крючком). 2. Рядом с пружиной или за ней установите и закрепите линейку с миллиметровыми делениями. 3. Отметьте и запишите то деление линейки, против которого приходится стрелка-указатель пружины. 4. Подвесьте к пружине груз известной массы и измерьте вызванное им удлинение пружины. 5. К первому грузу добавьте второй, третий и т. д. грузы, записывая каждый раз удлинение \ х\ пружины. По результатам измерений заполните таблицу ХОД РАБОТЫ:
№ опыта m, кг mg, H х, м 1 0,1 2 0,2 3 0,3 4 0,4
6. Начертите оси координат х и F, выберите удобный масштаб и нанесите полученные экспериментальные точки. 7. Оцените (качественно) справедливость закона Гука для данной пружины: находятся ли экспериментальные точки вблизи одной прямой, проходящей через начало координат. 8. По результатам измерений постройте график зависимости силы упругости от удлинения и, пользуясь им, определите среднее значение жесткости пружины k ср.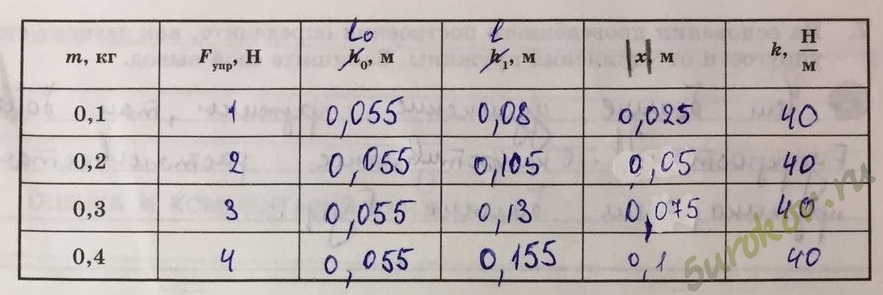 9. Рассчитайте наибольшую относительную погрешность, с которой найдено значение k cp 10. Запишите сделанный вами вывод.
9. Рассчитайте наибольшую относительную погрешность, с которой найдено значение k cp 10. Запишите сделанный вами вывод.
Контрольные вопросы: Как называется зависимость между силой упругости и удлинением пружины? Пружина динамометра под действием силы 4Н удлинилась на 5 мм. Определите вес груза, под действием которого эта пружина удлиняется на 16 мм.
Лабораторная работа.
Определение коэффициента жесткости пружины.
Цель работы: используя экспериментальную зависимость силы упругости от абсолютного удлинения, вычислить коэффициент жёсткости пружины.
Оборудование: штатив, линейка, пружина, грузы массой по 100 г.
Теория. Под деформацией понимают изменение объема или формы тела под действием внешних сил. При изменении расстояния между частицами вещества (атомами, молекулами, ионами) изменяются силы взаимодействия между ними. При увеличении расстояния растут силы притяжения, а при уменьшении – силы отталкивания, которые стремятся вернуть тело в исходное состояния. Поэтому силы упругости имеют электромагнитную природу. Сила упругости всегда направлена к положению равновесия и стремится вернуть тело в исходное состояние. Сила упругости прямо пропорциональна абсолютному удлинению тела.
Поэтому силы упругости имеют электромагнитную природу. Сила упругости всегда направлена к положению равновесия и стремится вернуть тело в исходное состояние. Сила упругости прямо пропорциональна абсолютному удлинению тела.
Закон Гука: Сила упругости, возникающая при деформации тела, прямо пропорциональна его удлинению (сжатию) и направлена противоположно перемещению частиц тела при деформации , F упр = кΔх , где k – коэффициент
жесткости [k] = Н/м, Δ х = Δ L – модуль удлинения тела.
Коэффициент жесткости зависит от формы и размеров тела,
а также от материала. Он численно равен силе упругости
при удлинении (сжатии) тела на 1 м.
Порядок выполнения работы.
1. Закрепить динамометр в штативе.
2. Измерить линейкой первоначальную длину пружины L 0 .
3 . Подвесить груз массой 100 г.
4. Измерить линейкой длину деформированной пружины L. Определить погрешность измерения длины: ΔƖ= 0,5дел*С 1 , где С 1 – цена деления линейки.
5. Вычислить удлинение пружины Δх = Δ L = L – L 0 .
6. На покоящийся относительно пружины груз действуют две компенсирующие друг друга силы: тяжести и упругости F т = F упр (смотри верхний рисунок )
7. Вычислить силу упругости по формуле , F упр = m g . Определить погрешность измерения силы: Δ F = 0,5дел*С 2 , где С 2 – цена деления динамометра.
8. Подвесить груз массой 200 г и повторить опыт по пунктам 4-6.
9. Подвесить груз массой 300 г и повторить опыт по пунктам 4-6.
10. Результаты занести в таблицу.
11. Вычислите коэффициент жесткости пружины для каждого измерения К= F упр / Δx и запишите в таблицу эти значения. Определите среднее значение К ср
12. Определите абсолютную погрешность измерения Δ к = ( Δ F / F упр + ΔƖ / L) * к измеренное , где Δ F – погрешность измерения силы, ΔƖ – погрешность измерения длины.
13. Выбрать систему координат и построить график зависимости силы упругости F упр от удлинения пружины Δ L .
Таблица измерения
п/п
Начальная длина, L 0, м
Конечная длина, L , м
Абсолютное удлинение Δ x 1 =Δ L = L – L 0, м
Сила упругости, F упр, Н
Коэффициент жёсткости, К, Н/м
14. Сделайте вывод. Полученный в результате опытов коэффициент жесткости пружины можно записать: к = к ср измеренное (у каждого ученика свой коэффициент) ± Δ к (для всех разная погрешность).
Сделайте вывод. Полученный в результате опытов коэффициент жесткости пружины можно записать: к = к ср измеренное (у каждого ученика свой коэффициент) ± Δ к (для всех разная погрешность).
Лабораторные работы по физике 9 класс Генденштейн Орлов Ход работы
1 — Закрепите конец пружины в штативе. Измерьте высоту на которой находится нижний конец пружины над столом.
2 — Подвесьте к пружине груз массой 100 грамм. Измерьте высоту, на которой находится теперь нижний конец пружины над столом. Вычислите удлинение пружины.
3 — Повторите измерения, подвешивая к пружине два, три и четыре грузы массой по 100 грамм.
4 — Запишите результаты в таблицу.
5 — Начертите систему координат для построения графика зависимости силы упругости от удлинения пружины.
7 — Определите, как зависит сила упругости от удлинения пружины.
Чем больше удлинение пружины, тем больше сила упругости, то есть чем длиннее растягивается пружина, тем больше сила упругости.
8 — По построенной прямой найдите жесткость пружины.
k = Fупр /|x|k = 4/0.1 = 40 H/m
9 — Определите, зависит ли жесткость пружины от ее длины, и если зависит, то как она изменяется при уменьшении длины пружины.
Жесткость пружины не зависит от удлинения длины пружины. У каждой пружины есть k(жесткость пружины) и она постоянна, не зависит от Fупр и от ΔxЛабораторная работа
«Определение жесткости пружины»
Цель работы : Определение коэффициента жесткости пружины. Проверка справедливости закона Гука.Оценка погрешности измерений.
Порядок выполнения работы .
Базовый уровень
Оборудование : штатив с муфтой и лапкой, набор грузов по 100 г, пружинный динамометр, линейка.
L 0 F
L 1 в этом случае.
l = L 0 — L 1
k ср .по формуле k ср =( k 1 + k 2 + k 3 )/3
F ,Н
l ,м
k ,Н/м
k ср , Н/м
6. Начертите график зависимости
l (
F ).
Начертите график зависимости
l (
F ).
Продвинутый уровень
Оборудование : штатив с муфтой и лапкой, набор грузов по 100 г, пружина, линейка.
Укрепите пружину в штативе и измерьте длину пружины L 0 в отсутствие внешнего воздействия (F =0Н). Результаты измерений запишите в таблицу.
Подвесьте к пружине груз весом 1 Н и определите ее длину L 1 в этом случае.
Найдите деформацию (удлинение) пружины по формуле l = L 0 — L 1 .Результаты измерений занесите в таблицу.
Аналогично найдите удлинение пружины при подвешивании грузов весом 2 Н и 3 Н. Результаты измерений занесите в таблицу.
Вычислите среднее арифметическое значение k ср .по формуле k ср =( k 1 + k 2 + k 3 )/3
Оцените погрешность ∆ k методом средней ошибки. Для этого вычислите модуль разности │ k ср — k i │=∆ k i для каждого измерения
k = k ср ±∆ k
F ,Н
l ,м
k ,Н/м
k ср , Н/м
∆k ,Н/м
∆k ср , Н/м
Углубленный уровень
Оборудование: штатив с муфтой и лапкой, набор грузов по 100 г, пружина, линейка.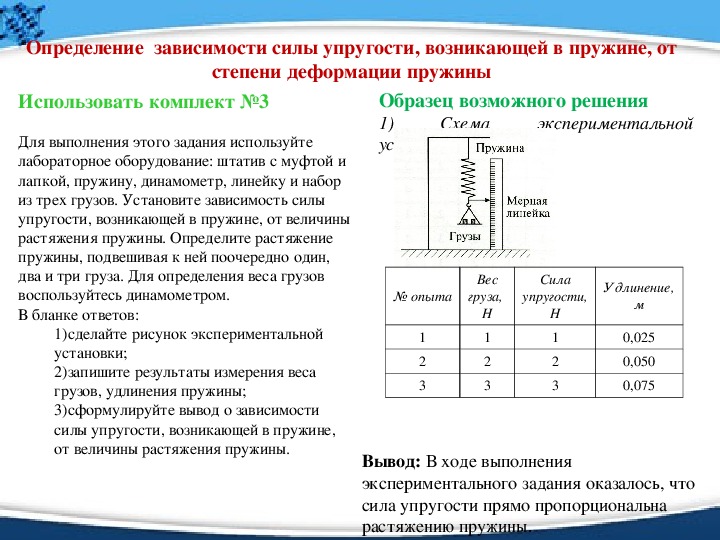
Укрепите пружину в штативе и измерьте длину пружины L 0 в отсутствие внешнего воздействия (F =0Н). Результаты измерений запишите в таблицу.
Подвесьте к пружине груз весом 1 Н и определите ее длину L 1 в этом случае.
Найдите деформацию (удлинение) пружины по формуле l = L 0 — L 1 .Результаты измерений занесите в таблицу.
Аналогично найдите удлинение пружины при подвешивании грузов весом 2 Н и 3 Н. Результаты измерений занесите в таблицу.
Вычислите среднее арифметическое значение k ср .по формуле k ср =( k 1 + k 2 + k 3 )/3
Вычислите относительные погрешности и абсолютную погрешность измерений ∆ k по формулам
ε F =(∆ F 0 + F и ) / F max
ε l =(∆ l 0 + l и ) / l max
ε k =ε F +ε l
∆k= ε k * k ср
Полученный результат запишите в виде k = k ср±∆ k
Начертите график зависимости
l (
F ). Сформулируйте геометрический смысл жесткости.
Сформулируйте геометрический смысл жесткости.
F ,Н
l ,м
k ,Н/м
k ср , Н/м
ε F
ε l
ε k
∆ k
Лабораторные работы по физике, 10 класс
1. Измерение ускорения тела при равноускоренном движении
Цель работы: измерить ускорение шарика, скатывающегося по наклонному желобу.
Оборудование: металлический желоб, стальной шарик, металлический цилиндр, измерительная лента, секундомер или часы с секундной стрелкой. (Для устойчивости к концам желоба можно приклеить кусочки ластика.)
Описание работы
Движение шарика, скатывающегося по желобу, можно приблизительно считать равноускоренным. При равноускоренном движении без начальной скорости модуль перемещения s, модуль ускорения a и время движения t связаны соотношением s = (at2)/2. Поэтому, измерив s и t, мы можем найти ускорение a по формуле a = (2s)/t2. Чтобы повысить точность измерения, ставят опыт несколько раз, а затем вычисляют средние значения измеряемых величин.
Ход работы
1. Положите желоб на стол, подложив под один из его концов одну или несколько тетрадей. Изменяя угол наклона желоба, добейтесь, чтобы шарик катился по нему достаточно медленно: движение вдоль всего желоба должно занимать не менее 3 с.
Положите в желоб у его нижнего конца металлический цилиндр. Когда шарик, скатившись, ударится о цилиндр, звук удара поможет точнее определить время движения шарика.
2. Отметьте на желобе начальное положение шарика, а также его конечное положение – верхний торец металлического цилиндра.
3. Измерьте расстояние между верхней и нижней отметками на желобе (модуль перемещения шарика s) и результат измерения запишите в таблицу, заголовок которой приведен ниже.
4. Отпустите шарик у верхней отметки без толчка и измерьте время t до удара шарика о цилиндр.
Повторите опыт 5 раз, записывая в таблицу результаты измерений. В каждом опыте пускайте шарик из одного и того же начального положения, а также следите за тем, чтобы верхний торец цилиндра находился у соответствующей отметки.
5. Вычислите tср = (t1 + t2 + t3 + t4 + t5) / 5 и результат запишите в таблицу.
6. Вычислите ускорение, с которым скатывался шарик: a ≈ (2s)/tср2. Результат вычислений запишите в таблицу.
7. Запишите выводы из эксперимента.
2. Изучение движения тела, брошенного горизонтально
Цели работы: 1) убедиться на опыте, что тело, брошенное горизонтально, движется по параболе; 2) измерить начальную скорость тела, брошенного горизонтально.
Оборудование: штатив с муфтой и зажимом, изогнутый желоб, металлический шарик, лист бумаги, лист копировальной бумаги, отвес, измерительная лента.
Описание работы
Шарик скатывается по изогнутому желобу, верхняя часть которого наклонная, а нижняя – горизонтальная (рис. 1). Оторвавшись от желоба, шарик под действием силы тяжести движется по параболе. Вершина этой параболы находится в точке, где шарик оторвался от желоба.
1). Оторвавшись от желоба, шарик под действием силы тяжести движется по параболе. Вершина этой параболы находится в точке, где шарик оторвался от желоба.
Выберем систему координат, как показано на рисунке.
При движении по параболе высота h, с которой падает шарик, и дальность полета l связаны соотношением h = (gl2)/(2v02). Отсюда следует, что при одинаковых начальных скоростях отношение высот, с которых падает шарик, должно быть равно отношению квадратов дальности полета.
Измерив h и l, можно найти скорость шарика в момент отрыва от желоба по формуле v0 = l√(g/(2h)).
Ход работы
1. Соберите установку, изображенную на рисунке Л-1. Нижний участок желоба должен быть горизонтальным, а расстояние h от нижнего края желоба до стола должно равняться 40 см. Лапки зажима расположите около верхнего конца желоба.
2. Положите под желобом лист бумаги, придавив его книгой, чтобы он не сдвигался при проведении опытов.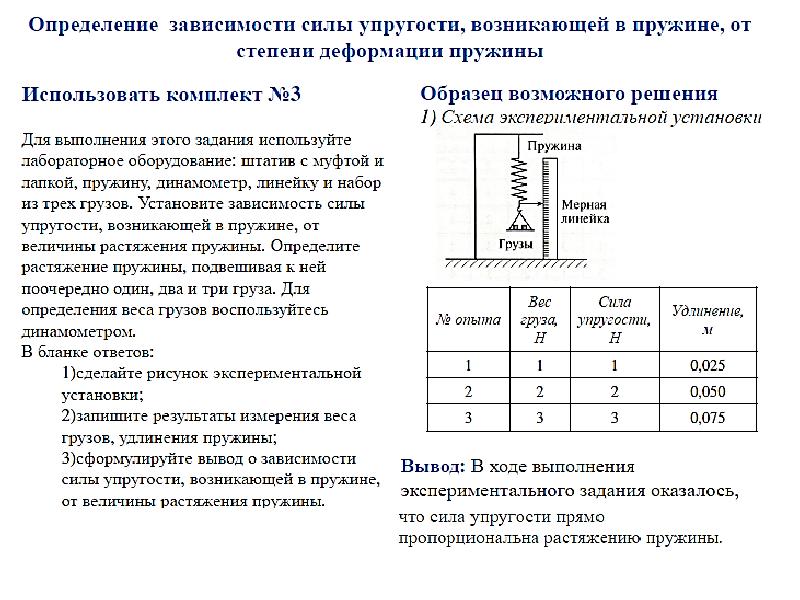 Отметьте на этом листе с помощью отвеса точку А, находящуюся на одной вертикали с нижним концом желоба.
Отметьте на этом листе с помощью отвеса точку А, находящуюся на одной вертикали с нижним концом желоба.
3. Поместите шарик в желоб так, чтобы он касался зажима штатива, и отпустите шарик без толчка. Заметьте (примерно) место на столе, куда упадет шарик. На отмеченное место положите лист бумаги, а на него – лист копировальной бумаги рабочей стороной вниз. Придавите эти листы книгой, чтобы они не сдвигались при проведении опытов.
4. Снова поместите шарик в желоб так, чтобы он касался зажима штатива, и отпустите без толчка. Повторите этот опыт 5 раз, следя за тем, чтобы лист копировальной бумаги и находящийся под ним лист не сдвигались. Снимите лист копировальной бумаги, не сдвигая листа под ним, и отметьте точку, расположенную наиболее близко ко всем отпечаткам (выбор этой точки означает усреднение результатов пяти опытов).
Учтите при этом, что некоторые отпечатки могут быть расположены очень близко друг к другу.
5. Измерьте расстояние l от отмеченной точки до точки А.
6. Опустите желоб так, чтобы его нижний край находился на высоте 10 см над столом, и повторите пункты 1–5. Измерьте соответствующее значение дальности полета и вычислите отношения h1/h2 и l1/l2.
7. Результаты измерений и вычислений запишите в таблицу, заголовок которой приведен ниже.
8. Проверьте, выполняется ли соотношение h1/h2 = l12/l22. Запишите расчет и сделайте вывод.
9. По результатам первого опыта вычислите значение v0, используя формулу v0 = l√(g/(2h)). Запишите расчет.
10. Запишите выводы из эксперимента.
3. Измерение жесткости пружины
Цели работы: 1) проверить справедливость закона Гука для пружины динамометра; 2) измерить жесткость этой пружины.
Оборудование: штатив с муфтой и зажимом, динамометр с заклеенной шкалой, набор грузов массой по 100 г, прозрачная линейка.
Описание работы
Согласно закону Гука модуль F силы упругости и модуль x удлинения пружины связаны соотношением F = kx.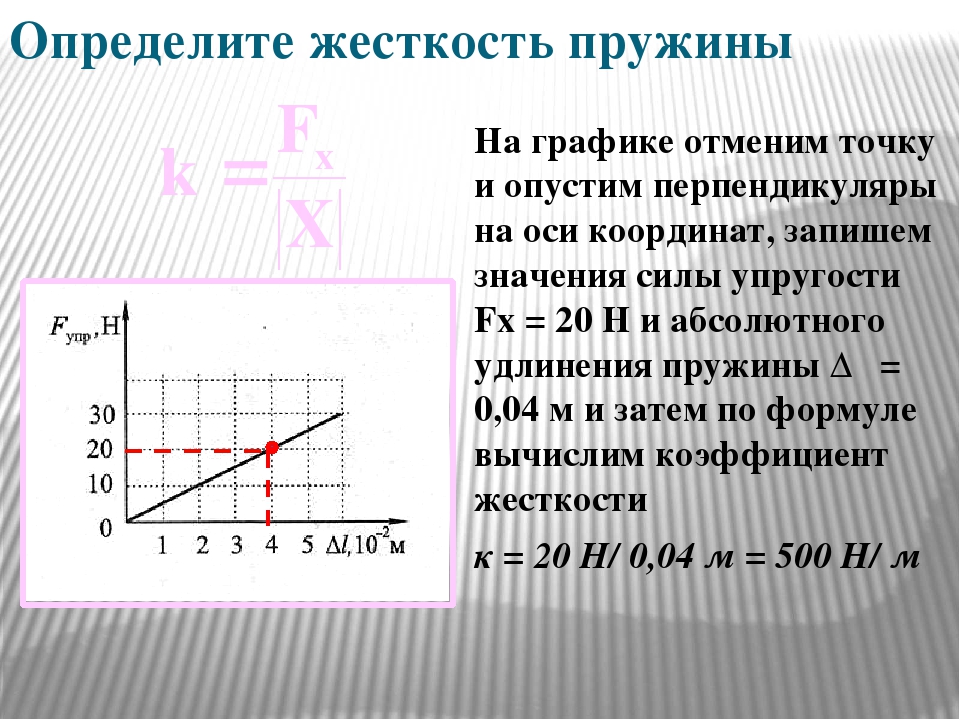 Измерив для конкретного случая F и x, можно найти коэффициент жесткости k по формуле k = F/x.
Измерив для конкретного случая F и x, можно найти коэффициент жесткости k по формуле k = F/x.
Ход работы
1. Закрепите динамометр в штативе на достаточно большой высоте над столом.
2. Подвешивая от одного до четырех грузов, вычислите для каждого случая значение силы упругости. Напомним, что в состоянии равновесия действующая на груз со стороны пружины сила упругости уравновешивается силой тяжести: F = mg. Измерьте также соответствующее удлинение пружины x.
3. Результаты измерений и вычислений запишите в таблицу, заголовок которой приведен ниже.
4. Начертите оси координат x и F, выбрав такой масштаб: 1 см удлинения пружины – 2 клетки и 1 Н силы упругости – 2 клетки. Нанесите полученные экспериментальные точки на координатную сетку.
5. С помощью прозрачной линейки проведите отрезок прямой, проходящий через начало координат как можно ближе к каждой из поставленных вами точек.
6. На основании этого построения определите, как зависит сила упругости от удлинения пружины. Запишите вывод.
Запишите вывод.
7. По графику зависимости силы упругости от удлинения пружины найдите жесткость пружины. Для наибольшей точности расчета следует взять точку на графике, наиболее удаленную от начала координат. Запишите расчет и результат.
8. Запишите выводы из эксперимента.
4. Определение коэффициента трения скольжения
Цели работы: 1) исследовать, от каких параметров зависит сила трения скольжения; 2) измерить коэффициент трения скольжения.
Оборудование: деревянная доска (или линейка), брусок, набор грузов массой по 100 г, динамометр.
Описание работы
Если равномерно тянуть брусок с грузом по горизонтальной поверхности, то прикладываемая к бруску горизонтальная сила будет равна по модулю силе трения скольжения Fтр, действующей на брусок со стороны поверхности. Модуль силы трения Fтр связан с модулем силы нормальной реакции N соотношением Fтр = μN. Измерив Fтр и N, можно найти коэффициент трения μ по формуле μ = Fтр/N.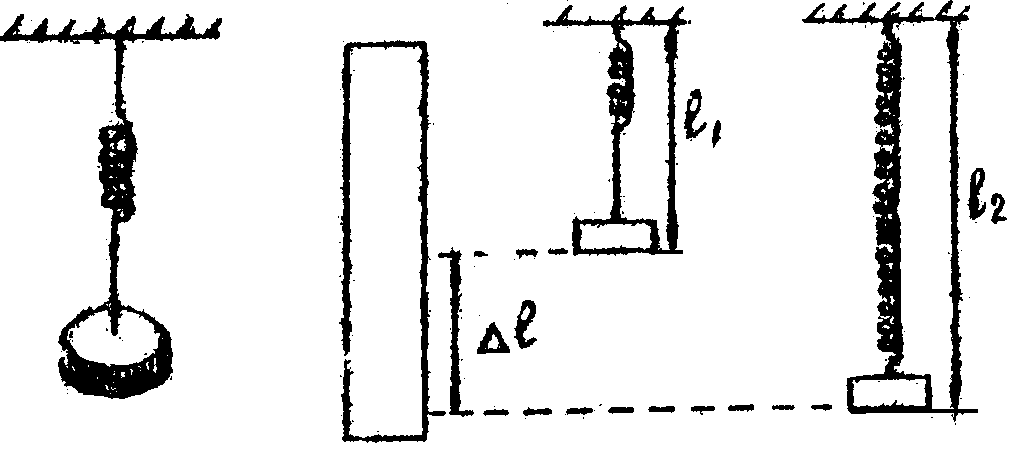
Ход работы
1. Измерьте вес бруска.
2. Положите брусок на горизонтальную деревянную поверхность так, чтобы с этой поверхностью соприкасалась самая большая грань бруска. Поставьте на брусок один груз и равномерно тяните брусок по поверхности с помощью динамо- метра, как показано на рисунке 1.
Запишите значение модуля силы нормальной реакции N и соответствующее ему значение модуля силы трения Fтр в таблицу, заголовок которой приведен ниже.
3. Повторите опыт, поставив на брусок два и затем три груза. Запишите результаты в таблицу.
4. Вычислите коэффициент трения между бруском и горизонтальной поверхностью во всех трех случаях (в пределах погрешности опыта результаты должны совпадать). Результаты опыта с тремя грузами обеспечивают наибольшую точность вычисления коэффициента трения. Расчет и результат запишите.
5. Запишите выводы из эксперимента.
5. Изучение закона сохранения энергии в механике
Цель работы: сравнить изменение потенциальной энергии груза с изменением потенциальной энергии пружины.
Оборудование: штатив с муфтой и зажимом, динамометр с фиксатором, груз, прочная нить, измерительная лента или линейка с миллиметровыми делениями.
Описание работы
Груз весом P прикрепляют с помощью нити к крючку пружины динамометра. Затем его поднимают на такую высоту h1 над поверхностью стола, чтобы нить провисала (рис. 3). Когда груз отпускают, он движется вниз и растягивает пружину. Измеряют высоту груза h2 над поверхностью стола, а также удлинение пружины x в тот момент, когда оно максимально (в этот момент скорость груза и, следовательно, его кинетическая энергия равны нулю).
При движении груза вниз его потенциальная энергия уменьшается на |∆Eгр| = P(h1 – h2), зато потенциальная энергия пружины увеличивается на Eпр = (kx2)/2, где k – жесткость пружины, x – максимальное удлинение пружины.
При движении груза вниз часть его потенциальной энергии переходит во внутреннюю вследствие трения в динамометре и сопротивления воздуха, поэтому Eпр < |∆Eгр|.
Потенциальная энергия деформированной пружины Eпр = (Fx)/2; где x – максимальное удлинение пружины, а F – соответствующая ему сила упругости. (При выводе формулы для потенциальной энергии деформированной пружины надо учесть, что среднее значение силы упругости при растяжении пружины равно F/2.) Таким образом, чтобы найти отношение Eпр/|∆Eгр|, надо измерить P, h1, h2, F и x.
Для измерения F, x и h2 необходимо отметить максимальное удлинение пружины. Для этого на стержень динамометра около ограничительной скобы надевают кусочек картона (фиксатор), который может перемещаться вдоль стержня с небольшим трением. При движении груза вниз ограничительная скоба динамометра переместит фиксатор вверх по стержню динамометра. Чтобы измерить максимальную силу упругости, надо затем растянуть динамометр рукой так, чтобы фиксатор оказался снова у ограничительной скобы. По значению максимальной силы упругости F можно определить значения x и h2.
Ход работы
1. Соберите установку, изображенную на рисунке 2.
2. Привяжите груз на нити длиной 12–15 см к крючку динамометра. Закрепите динамометр в зажиме штатива на такой высоте, чтобы груз при максимальном растяжении пружины динамометра не доставал до стола.
3. Приподняв груз так, чтобы нить провисала, установите фиксатор на стержне динамометра около ограничительной скобы (рис. 3, а). Отпустив груз, убедитесь в том, что при максимальном растяжении пружины она не достает до ограничительной скобы (в противном случае при неупругом ударе пружины об ограничительную скобу произойдет превращение значительной части ее механической энергии во внутреннюю). Если это условие не выполняется, уменьшите начальную высоту груза.
4. Поднимите груз и измерьте высоту h1, на которой находится нижняя грань груза.
5. Отпустите груз без толчка. Падая, груз растянет пружину, и фиксатор переместится по стержню вверх. Затем, растянув рукой пружину так, чтобы фиксатор оказался у ограничительной скобы, измерьте F, x и h2.
6. Вычислите: а) вес груза P = mg; б) увеличение потенциальной энергии пружины Eпр = (Fx)/2; в) модуль уменьшения потенциальной энергии груза |∆Eгр| = P(h1 – h2).
7. Результаты измерений и вычислений запишите в таблицу, заголовок которой приведен ниже.
8. Найдите значение отношения Eпр/|∆Eгр| и сравните его с единицей. Расчет и результат запишите.
9. Запишите выводы из эксперимента.
Постоянная пружины и калибровка чувствительности кантилеверов микропипеток FluidFM для измерений силовой спектроскопии
Колебания в
k и InvOLS в зависимости от положения лазерного пятна Во-первых, мы исследовали влияние положения пятна лазерного луча на измеренные значения InvOLS для всех кантилеверов . На рис. 4 представлены результаты, полученные на подложках из полистирола и кремния. Следует отметить, что теоретически полученные значения InvOLS должны демонстрировать тенденцию к монотонному увеличению 24 в зависимости от положения пятна от вершины к основанию, в соответствии с деформацией кантилевера по его длине.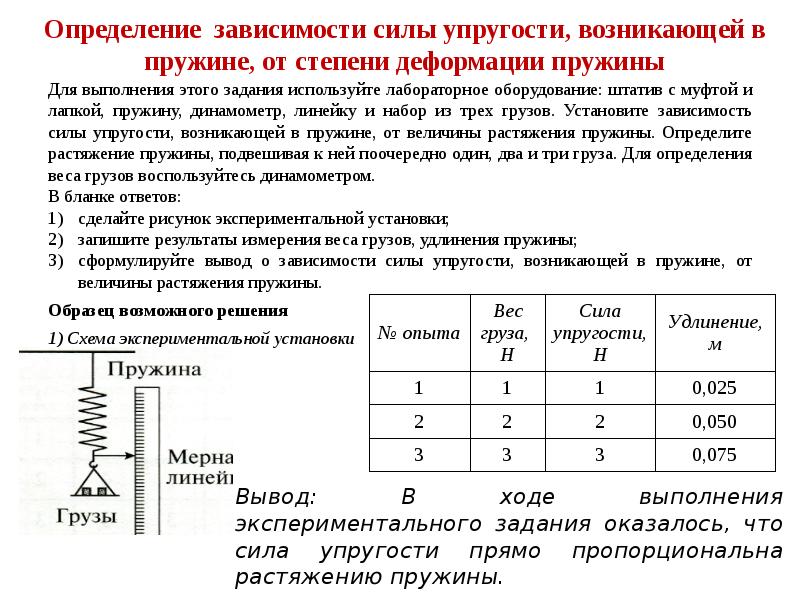 Вместо этого мы наблюдали периодические колебания, которые накладываются на тенденцию к увеличению длины кантилеверов. Это колебание явно может быть связано с нерегулярной внутренней структурой консолей микропипеток FluidFM, которые отличаются от обычных пластинчатых консолей АСМ 25 с характерной монотонной чувствительностью рычага 24,28 кривых. Консоли FluidFM включают наножидкостный канал, поддерживаемый параллельными рядами стоек для повышения устойчивости 25 .Можно установить, что напряжения, развивающиеся в полой консоли, и ее последующая деформация, вызванная вдавливанием, не будут однородными по ее длине. Столбы имеют диаметр 3 мкм и равномерно расположены через каждые 10 мкм (см. Рис. 3). Однако диаметр лазерного пятна достаточно велик (около 22 мкм с гауссовым распределением интенсивности), чтобы освещать более одной пары столбов одновременно. Локальная деформация кантилевера, распределение интенсивности лазерного пятна и возможные интерференционные эффекты вместе определяют измеренный сигнал отклонения от одного пятна, который нелегко предсказать или рассчитать.
Вместо этого мы наблюдали периодические колебания, которые накладываются на тенденцию к увеличению длины кантилеверов. Это колебание явно может быть связано с нерегулярной внутренней структурой консолей микропипеток FluidFM, которые отличаются от обычных пластинчатых консолей АСМ 25 с характерной монотонной чувствительностью рычага 24,28 кривых. Консоли FluidFM включают наножидкостный канал, поддерживаемый параллельными рядами стоек для повышения устойчивости 25 .Можно установить, что напряжения, развивающиеся в полой консоли, и ее последующая деформация, вызванная вдавливанием, не будут однородными по ее длине. Столбы имеют диаметр 3 мкм и равномерно расположены через каждые 10 мкм (см. Рис. 3). Однако диаметр лазерного пятна достаточно велик (около 22 мкм с гауссовым распределением интенсивности), чтобы освещать более одной пары столбов одновременно. Локальная деформация кантилевера, распределение интенсивности лазерного пятна и возможные интерференционные эффекты вместе определяют измеренный сигнал отклонения от одного пятна, который нелегко предсказать или рассчитать. Однако два важных факта можно сделать на основании результатов на рис. 4: (1) флуктуация InvOLS в зависимости от положения лазера является последовательной и повторяемой; измерения, независимо выполненные на двух разных подложках, согласовывались друг с другом. (2) Калибровка на пластине из полистирола не привела к существенной разнице по сравнению с идеально плоской и твердой кремниевой пластиной. Это подтверждает, что пластиковая пластина также может использоваться для калибровки.
Однако два важных факта можно сделать на основании результатов на рис. 4: (1) флуктуация InvOLS в зависимости от положения лазера является последовательной и повторяемой; измерения, независимо выполненные на двух разных подложках, согласовывались друг с другом. (2) Калибровка на пластине из полистирола не привела к существенной разнице по сравнению с идеально плоской и твердой кремниевой пластиной. Это подтверждает, что пластиковая пластина также может использоваться для калибровки.
Полученные значения InvOLS, измеренные с шагом 10 мкм на подложках из полистирола и кремния, в зависимости от положения лазера для кантилеверов FluidFM с ( A ) 2 мкм, ( B ) 4 мкм и ( C) ) Апертуры 8 мкм.Точки данных представляют собой среднее значение и стандартное отклонение 10 последовательных измерений в каждой точке. Пунктирные линии показывают среднее значение для данного кантилевера с учетом всех данных.
Интересный аспект кривых на рис. 4 состоит в том, что периодичность флуктуации не следует непосредственно за периодичностью столбов в канале 10 мкм. Чтобы исследовать это более подробно, мы повторили эксперименты и измерили InvOLS с более тонким разрешением 1 мкм, используя только пластину PS и сосредоточив внимание только на наиболее важной области кантилевера: ближайшей к наконечнику, где большинство пользователей размещают свои лазер.Опять же, исходное положение (0 мкм) выбирается так, чтобы оно находилось непосредственно над первой парой стоек (см. Рис. 3B, C). Отрицательные положения означают, что максимум интенсивности пятна был расположен между концом кантилевера и первой парой столбов (рис. 3). Размещение лазера непосредственно на апертурах приведет к увеличению помех и шума, особенно для кантилеверов с большими размерами апертуры, что приведет к неизменно ненадежным значениям чувствительности (эти значения были отброшены).
4 состоит в том, что периодичность флуктуации не следует непосредственно за периодичностью столбов в канале 10 мкм. Чтобы исследовать это более подробно, мы повторили эксперименты и измерили InvOLS с более тонким разрешением 1 мкм, используя только пластину PS и сосредоточив внимание только на наиболее важной области кантилевера: ближайшей к наконечнику, где большинство пользователей размещают свои лазер.Опять же, исходное положение (0 мкм) выбирается так, чтобы оно находилось непосредственно над первой парой стоек (см. Рис. 3B, C). Отрицательные положения означают, что максимум интенсивности пятна был расположен между концом кантилевера и первой парой столбов (рис. 3). Размещение лазера непосредственно на апертурах приведет к увеличению помех и шума, особенно для кантилеверов с большими размерами апертуры, что приведет к неизменно ненадежным значениям чувствительности (эти значения были отброшены).
Из результатов рис. 5A можно увидеть, что, хотя три кантилевера с разными размерами апертуры привели к разной абсолютной чувствительности, их тенденции — выделенные полиномиальной подгонкой наборов данных — работают вместе. InvOLS имеет определенный локальный минимум на первой паре столбов (0 мкм), то есть деформация кантилевера здесь наибольшая. Следующий локальный минимум находится около третьих столбов, между этими двумя обратная чувствительность имеет локальный максимум около второй пары столбов.
InvOLS имеет определенный локальный минимум на первой паре столбов (0 мкм), то есть деформация кантилевера здесь наибольшая. Следующий локальный минимум находится около третьих столбов, между этими двумя обратная чувствительность имеет локальный максимум около второй пары столбов.
( A ) Полученные значения InvOLS, измеренные с шагом 1 мкм на полистирольной подложке с тремя консолями FluidFM. Кривые представляют собой полиномиальную аппроксимацию 5 -го уровня для наборов данных. ( B ) Жесткость пружины, измеренная с шагом 1 мкм в воздухе с помощью трех консолей FluidFM, в зависимости от положения лазерного пятна.
Важно подчеркнуть, что наблюдаемая тенденция синусоидальных колебаний на кривых InvOLS (рис.5A) зависит от структурных характеристик и деформации датчиков FluidFM и не зависит от шума, наложенного на кривые отклонения. Из кривой прогиба образца, представленной на рис. 1В, видно, что присутствует шум, возникающий из-за лазерной интерференции. Как упоминалось ранее, этот эффект наиболее силен над отверстиями и, по-видимому, уменьшается по длине кантилеверов. Чтобы количественно оценить этот шум, мы рассчитали среднеквадратическую ошибку (MSE) линейной аппроксимации для базовой линии (рис.6A), а также для линейного участка вдавливания (фиг. 6B) кривых прогиба (см. Фиг. 1B для иллюстрации). Результаты показывают, что уровень шума падает на несколько порядков по кантилеверу (от апертуры до третьей стойки), но только на базовой линии. Шум, накладываемый на линейную часть кривых отклонения, не зависит от положения лазерного пятна вдоль кантилевера, что подтверждает наши выводы относительно рис. 5А.
Как упоминалось ранее, этот эффект наиболее силен над отверстиями и, по-видимому, уменьшается по длине кантилеверов. Чтобы количественно оценить этот шум, мы рассчитали среднеквадратическую ошибку (MSE) линейной аппроксимации для базовой линии (рис.6A), а также для линейного участка вдавливания (фиг. 6B) кривых прогиба (см. Фиг. 1B для иллюстрации). Результаты показывают, что уровень шума падает на несколько порядков по кантилеверу (от апертуры до третьей стойки), но только на базовой линии. Шум, накладываемый на линейную часть кривых отклонения, не зависит от положения лазерного пятна вдоль кантилевера, что подтверждает наши выводы относительно рис. 5А.
( A ) Уровни шума, рассчитанные как среднеквадратичная ошибка (MSE) линейной аппроксимации базовой линии кривой силы (см. Рис.1Б). ( B ) Те же MSE, измеренные на участке линейного вдавливания (приближения) кривой силы, который использовался для расчетов InvOLS.
С тем же разрешением была измерена жесткость пружины, что было оценено встроенным методом Садера ARYA. Результаты представлены на фиг. 5В. Опять же, кривые показывают аналогичные тенденции (например, определенный пик около 15 мкм), но их значение требует дальнейшего изучения.
Результаты представлены на фиг. 5В. Опять же, кривые показывают аналогичные тенденции (например, определенный пик около 15 мкм), но их значение требует дальнейшего изучения.
Жесткость пружины — это фундаментальный атрибут кантилевера, определяемый свойствами материала и конструкции, которые теоретически не должны зависеть от положения пятна лазерного луча.Таким образом, наблюдаемая флуктуация на рис. 5B должна возникать только из-за ошибок измерения. Как обсуждалось ранее (уравнение 3), метод Садера требует в качестве входных параметров положения и добротности (резонансной частоты / ширины полосы) первого основного резонансного пика, полученных из спектра теплового шума кантилевера. Можно предположить, что изменение расчетной жесткости пружины в зависимости от положения лазера в первую очередь может быть связано с неопределенностью определения добротности из-за изменения уровней шума по длине кантилевера.Представленные на рис. 7 спектры теплового шума подтверждают это предположение.
( A ) Необработанные спектры теплового шума кантилевера с размером апертуры 4 мкм, непосредственно экспортированные из ARYA, полученные при четырех различных положениях лазерного пятна (см. Рис. 5B). ( B ) Подгоняемые функции пиков Лоренца, также экспортированные из ARYA. ( C ) Нормализованный пик функционирует в тех же положениях. ( D ) Необработанные спектры теплового шума и аппроксимированные функции лоренцевского пика построены вместе в двух последовательных положениях (MSE: среднеквадратичная ошибка).
На рис. 7A представлены четыре спектра теплового шума (напрямую экспортированные из ARYA), измеренные в последовательных положениях, соответствующих данным, представленным на рис. 5B (размер апертуры кантилевера: 4 мкм). На рисунке 7B показаны функции подобранных пиков Лоренца, также экспортированные из ARYA. Константы пружины, рассчитанные с помощью программного обеспечения, также представлены на рисунках. Их вариативность высока, например разница минимум-максимум между двумя последовательными положениями @ 12 и @ 13 мкм составляет 0,41 Н / м, что составляет 20% относительной разницы.На фиг. 7А видно, что полученные спектры довольно зашумлены. Положения пиков не сильно меняются, и поэтому резонансные частоты идентифицируются правильно (изменение ниже 7 Гц), но шум явно влияет на определение ширины полосы, определяемой как полная ширина на полувысоте (FWHM). На фиг. 7C приведены нормализованные вручную амплитудные спектры из фиг. 7B вместе с коэффициентами качества ( Q ), рассчитанными ARYA. Данные подтверждают, что изменение жесткости пружины происходит из определения FWHM, как показано на рис.7D в двух последовательных позициях. Оба спектра зашумлены, но в то время как в случае @ 12 мкм функция лоренцевского пика аппроксимируется на внешней границе зашумленных краев, при @ 13 мкм подобранная кривая следует по внутренней границе. Это приводит к уменьшению FWHM во втором случае и к более высокой жесткости пружины в этом положении.
Их вариативность высока, например разница минимум-максимум между двумя последовательными положениями @ 12 и @ 13 мкм составляет 0,41 Н / м, что составляет 20% относительной разницы.На фиг. 7А видно, что полученные спектры довольно зашумлены. Положения пиков не сильно меняются, и поэтому резонансные частоты идентифицируются правильно (изменение ниже 7 Гц), но шум явно влияет на определение ширины полосы, определяемой как полная ширина на полувысоте (FWHM). На фиг. 7C приведены нормализованные вручную амплитудные спектры из фиг. 7B вместе с коэффициентами качества ( Q ), рассчитанными ARYA. Данные подтверждают, что изменение жесткости пружины происходит из определения FWHM, как показано на рис.7D в двух последовательных позициях. Оба спектра зашумлены, но в то время как в случае @ 12 мкм функция лоренцевского пика аппроксимируется на внешней границе зашумленных краев, при @ 13 мкм подобранная кривая следует по внутренней границе. Это приводит к уменьшению FWHM во втором случае и к более высокой жесткости пружины в этом положении. Ошибка подгонки (рассчитанная как среднеквадратичная ошибка (MSE) между исходными данными и лоренцевой подгонкой, также приведенная на рис. 7D) меньше для @ 12 мкм, таким образом, полученная жесткость пружины может считаться более надежной в этом положении.Подробный анализ зависимости рассчитанной жесткости пружины от измеренного значения ω R и FWHM см. В дополнительной информации (S1). Ошибка встроенной функции оценки пика также сравнивается с ручной оценкой пика в S2.
Ошибка подгонки (рассчитанная как среднеквадратичная ошибка (MSE) между исходными данными и лоренцевой подгонкой, также приведенная на рис. 7D) меньше для @ 12 мкм, таким образом, полученная жесткость пружины может считаться более надежной в этом положении.Подробный анализ зависимости рассчитанной жесткости пружины от измеренного значения ω R и FWHM см. В дополнительной информации (S1). Ошибка встроенной функции оценки пика также сравнивается с ручной оценкой пика в S2.
На рис. 5В показано, что определенные жесткие пружины сильно различаются в зависимости от положения лазерного пятна вдоль кантилевера, и чтобы определить, какие значения можно считать приемлемыми, мы построили график среднеквадратичной ошибки (СКО) функция лоренцевского пика (выполненная ARYA) на рис.8A в зависимости от вычисленных значений жесткости пружины. Этот MSE можно рассматривать как характеристику уровня шума, который накладывается на тепловые спектры вдоль кантилевера.
Рис. 8
8 ( A ) Среднеквадратичная ошибка (MSE), вычисленная между исходным тепловым спектром и его лоренцевой аппроксимацией, как функции рассчитанной жесткости пружины (данные соответствуют рис. 5B). Стрелки указывают выбранные справочные значения, используемые для изменения масштаба наборов данных, как показано на рис.8B. Пунктирные линии представляют собой среднее значение каждого распределения. ( B ) Относительные значения жесткости пружины в зависимости от положения лазера. В расчетах использовались следующие значения (100%): 1,51 Н / м для 8 мкм, 1,87 Н / м для 4 мкм и 1,31 Н / м для апертуры 2 мкм соответственно.
Важно отметить, что значения жесткости пружины, рассчитанные в местах наименьшей погрешности, хорошо совпадают со средним значением их распределений для отверстий 2 и 8 мкм (рис.8А). Для кантилевера с апертурой 4 мкм также хорошо определено место наименьшей погрешности в зависимости от жесткости пружины. На фиг. 8B эти три значения, отмеченные стрелками, использовались в качестве эталона (100%) для расчета относительных значений жесткости пружины как функции положения лазерного пятна.
Можно видеть, что отдельные кривые на рис. 5B теперь накладываются друг на друга в определенном тренде. Первое пересечение этого общего тренда со 100% линией (пунктирная на рис. 8B) плотно прилегает к первому столбу (0 мкм, отмечен красным кружком), и хотя последующие пересечения также примерно совпадают со вторым (10 мкм) и третьей (20 мкм) опоры, эти пересечения размыты, и здесь вносимая ошибка может быть намного выше.(Обратите внимание, что диаметр столба составляет 3 мкм, а точность данных позиций составляет около 1 мкм).
Стратегия калибровки
Данные, представленные в предыдущем разделе, могут быть использованы для разработки стратегии калибровки полых кантилеверов FluidFM. Хотя очевидно, что измеренные колебания как InvOLS, так и жесткости пружины довольно высоки (около ± 30% для InvOLS (рис. 5A) и -13 / + 20% для жесткости пружины (рис. 8B), их значение и значимость являются совершенно разные, и поэтому к ним следует относиться по-разному.
InvOLS характеризует локальный прогиб кантилевера. Более низкий InvOLS означает более высокую чувствительность к силе, но пользователю не обязательно минимизировать InvOLS, чтобы иметь надежные данные. Если это определено правильной калибровкой в любом положении (например, кривая прогиба в точке измерения не имеет шума и линейная аппроксимация правильная), ее можно использовать для масштабирования впоследствии измеренных кривых прогиба (уравнение 1) независимо от ее абсолютного значения. значение, не привнося ошибки в собранные данные.Единственная распространенная ошибка, которую может сделать пользователь, — это использовать «общий» InvOLS для кантилевера вместо измерения местного InvOLS в точном положении лазерного пятна. В качестве примера: среднее значение InvOLS с учетом всей длины кантилевера составляет около 2,3 мкм / В (рис. 4). Если использовать это как общее значение для своих кантилеверов, а затем поместить лазер поверх первой пары столбов на кантилевере с апертурой 2 мкм, то для всех впоследствии измеренных данных силы будет непосредственно введена ошибка -30%.
Более низкий InvOLS означает более высокую чувствительность к силе, но пользователю не обязательно минимизировать InvOLS, чтобы иметь надежные данные. Если это определено правильной калибровкой в любом положении (например, кривая прогиба в точке измерения не имеет шума и линейная аппроксимация правильная), ее можно использовать для масштабирования впоследствии измеренных кривых прогиба (уравнение 1) независимо от ее абсолютного значения. значение, не привнося ошибки в собранные данные.Единственная распространенная ошибка, которую может сделать пользователь, — это использовать «общий» InvOLS для кантилевера вместо измерения местного InvOLS в точном положении лазерного пятна. В качестве примера: среднее значение InvOLS с учетом всей длины кантилевера составляет около 2,3 мкм / В (рис. 4). Если использовать это как общее значение для своих кантилеверов, а затем поместить лазер поверх первой пары столбов на кантилевере с апертурой 2 мкм, то для всех впоследствии измеренных данных силы будет непосредственно введена ошибка -30%. Общее правило калибровки InvOLS состоит в том, что необходимо всегда использовать локальный InvOLS полого кантилевера и не изменять положение лазерного пятна между калибровкой и измерениями.
Общее правило калибровки InvOLS состоит в том, что необходимо всегда использовать локальный InvOLS полого кантилевера и не изменять положение лазерного пятна между калибровкой и измерениями.
Жесткая пружина — совсем другое дело. Как обсуждалось ранее, это основной параметр кантилевера, который не должен изменяться в зависимости от положения лазера. Определение реальной жесткости пружины для кантилевера необходимо: даже для гораздо более простых традиционных кантилеверов AFM реальная жесткость пружины может значительно отличаться от номинального значения, указанного производителем, из-за технологических отклонений.Представленные нами данные на рис. 8A также подтвердили, что реальная жесткость пружины трех использованных консолей (с учетом значений, полученных с наименьшей ошибкой лоренцевой аппроксимации тепловых спектров как « реальные » значения жесткости пружины) значительно отличались от их номинальных значений. 2 Н / м (1,51 Н / м для 8 мкм, 1,87 Н / м для 4 мкм и 1,31 Н / м для размера апертуры 2 мкм соответственно). (Примечание: полученные различия в измеренных значениях жесткости пружины являются следствием технологических изменений и не характерны для размеров отверстий.Настоящая проблема заключается в том, что, как мы продемонстрировали на рис. 8B, калибровка жесткости пружины в неправильном положении может привести к добавленной ошибке −13 / + 20%, и на этом этапе надежность калибровки (или ошибка лоренцевой подгонки ) не могут быть непосредственно оценены в программе ARYA.
(Примечание: полученные различия в измеренных значениях жесткости пружины являются следствием технологических изменений и не характерны для размеров отверстий.Настоящая проблема заключается в том, что, как мы продемонстрировали на рис. 8B, калибровка жесткости пружины в неправильном положении может привести к добавленной ошибке −13 / + 20%, и на этом этапе надежность калибровки (или ошибка лоренцевой подгонки ) не могут быть непосредственно оценены в программе ARYA.
На основании представленных данных и предыдущих обсуждений мы рекомендуем следующую стратегию калибровки :
- (1).
Хорошее место для надежной калибровки жесткости пружины находится на первых столбах .
- (2).
Рекомендуется перейти к третьей стойке после калибровки жесткости пружины. , , откалибруйте здесь InvOLS и выполните измерения . Общий шум, возникающий из-за лазерных помех, здесь меньше.
- (3).
Для наиболее надежной калибровки жесткости пружины мы советуем расположить лазер на первой паре стоек , , затем перемещать лазер в диапазоне ± 2–3 мкм и повторять калибровку с шагом 1 мкм .
 Хотя точность лоренцевой аппроксимации тепловых спектров не отображается в программном обеспечении, необработанные и подогнанные кривые можно экспортировать, а среднеквадратическую ошибку можно вычислить вручную, чтобы найти положение, в котором шум является наименьшим, и, следовательно, отображаемую жесткость пружины. самый надежный.
Хотя точность лоренцевой аппроксимации тепловых спектров не отображается в программном обеспечении, необработанные и подогнанные кривые можно экспортировать, а среднеквадратическую ошибку можно вычислить вручную, чтобы найти положение, в котором шум является наименьшим, и, следовательно, отображаемую жесткость пружины. самый надежный. - (4).
InvOLS можно измерить локально , , но не перемещайте лазер после (между калибровкой и последующими измерениями).
Исследование в поддержке взаимодействия наземной поддержки путем численного моделирования и лабораторных испытаний
ASTM D2487 (2011) Стандартная практика для классификации почв для технических целей (единой системы классификации почв).ASTM International, West Conshohocken, PA
Google ученый
ASTM D3080 (2011) Метод испытания грунтов на прямой сдвиг в условиях консолидированного дренажа. ASTM International, West Conshohocken, PA
Google ученый
ASTM D6913 (2004) Стандартные методы испытаний для гранулометрического состава (градации) почв с использованием ситового анализа. ASTM International, West Conshohocken, PA
Google ученый
Brady BHG, Brown ET (1993) Механики горных пород для подземных горных работ.Chapman & Hall, Лондон
Google ученый
Cruz D (2014) Геомеханический отклик аксиально нагруженных анкерных болтов, полностью залитых с помощью волоконной оптики. MASc, Королевский военный колледж Канады, Кингстон, ON
MASc, Королевский военный колледж Канады, Кингстон, ON
Google ученый
Cruz D, Vlachopoulos N, Forbes B (2016) Геомеханический отклик осевых анкерных болтов с использованием оптоволоконной технологии.В: XV Колумбийский геотехнический конгресс и II международная специализированная конференция мягких пород. Картахена, Колумбия
Doucet C, Voyzelle B (2012) Листы технических данных. Natural Resources Canada, Оттава
Google ученый
Фермер И. В. (1975) Распределение напряжений вдоль залитого смолой каменного анкера. Int J Rock Mech Min Sci 12: 347–351
Статья Google ученый
Forbes B (2015) Применение распределенного оптического зондирования для поддержки мониторинга в подземных выработках.Магистр наук, Королевский университет, Кингстон
Forbes B, Vlachopoulos N, Oke J, Hyett AJ (2014) Применение распределенного оптического зондирования для мониторинга схем временной поддержки. Канадское геотехническое общество, GeoRegina, Regina, SK
Google ученый
Funatsu T, Hoshino T, Sawae H, Shimizu N (2008) Численный анализ для лучшего понимания механизма воздействия наземных опор и арматуры на устойчивость туннелей с использованием метода отдельных элементов.Tunn Undergr Space Technol Inc Trenchless Technol Res 23 (5): 561–573
Статья Google ученый
Gervais JRD (2003) Обычаи и традиции канадских военных инженеров. DND, Оттава
Google ученый
Газвинян Э., Дидерикс М.С., Лабри Д., Мартин С.Д. (2015) Исследование зависимости пороговых значений трещинного повреждения от типа ткани в хрупких породах.Geotech Geol Eng 33 (июль): 1409
Статья Google ученый
Hoek E (2014) Анкерные болты и тросы. Неизвестно, Неизвестно
Google ученый
Holt SW (2017) Определение и влияние параметров прочности на сдвиг поверхностей раздела материалов, связанных с наземными системами поддержки. Магистр наук, Королевский военный колледж Канады
Holt SW, Vlachopoulos N, Forbes B (2016) Определение параметров взаимодействия раствора с грунтом для наземных опорных элементов.ГеоВанкувер, Канада
Google ученый
Hyett AJ, Bawden WF, Reichert RD (1992) Влияние ограничения горной массы на прочность сцепления полностью залитых раствором кабельных болтов. В: Международный журнал механики горных пород, горных наук и геомеханики, т. 29, № 5, стр. 503–524
Itasca Consulting Group Inc (2009) Быстрый лагранжев анализ континуумов в 3 измерениях, версия 4.0. Itasca Consulting Group Inc., Миннеаполис
Google ученый
Li C, Stillborg B (1999) Аналитические модели для анкерных болтов. Int J Rock Mech Min Sci 36 (8): 1013–1029
Int J Rock Mech Min Sci 36 (8): 1013–1029
Статья Google ученый
Маринос П., Хук Э. (2001) Надлежащее использование геологической информации при проектировании и строительстве туннелей на автомагистрали Эгнатия. Egnatia Odos A.E.
Oke J, Vlachopoulos N, Diederichs MS (2012) Улучшенные входные параметры и методы численного анализа для временной поддержки подземных выработок в слабых породах.В: RockEng. Эдмонтон, Канада
Оке Дж., Влахопулос Н., Дидерикс М.С. (2014a) Численный анализ при проектировании систем зонтичных арок. J Rock Mech Geotech Eng 6 (6): 546
Артикул Google ученый
Oke J, Vlachopoulos N, Marinos V (2014b) Номенклатура предварительной поддержки и методология выбора поддержки для временных систем поддержки в слабых горных массивах. J Geotech Geol Eng 32 (1): 97e130
Статья Google ученый
Serbousek MO, Signer SP (1987) Линейная механика передачи нагрузки полностью залитых анкерными болтами, том 9135.Министерство внутренних дел США, Горное управление
Терзаги К., Пек Р.Б., Месри Г. (1996) Механика грунтов в инженерной практике. Уайли, Хобокен
Google ученый
Trinh QN (2006) Анализ проблемы обрушения в туннеле гидроэлектростанции во Вьетнаме. Кандидат наук. Тезис. Норвежский университет науки и технологий, Тронхейм, Норвегия
Кандидат наук. Тезис. Норвежский университет науки и технологий, Тронхейм, Норвегия
Влахопулос Н. (2000) Выполнение двух натурных моделей подпорных стен, армированных геосинтетическим материалом: сегментной и облицованной.MASc, Королевский военный колледж Канады, Кингстон, ON
Vlachopoulos N (2009) Обратный анализ ситуационного исследования проходки туннелей в слабых породах альпийской системы на севере Греции: проверка и оптимизация расчетного анализа на основе характеристик грунта и численных моделирование. Кандидат наук. Тезис. Queens University, Kingston, Ontario
Vlachopoulos N, Cruz D, Forbes B (2018) Использование новой волоконно-оптической технологии для определения осевого отклика полностью залитых анкерами. J Rock Mech Geotech Eng 10 (2): 222–235
J Rock Mech Geotech Eng 10 (2): 222–235
Статья Google ученый
Фолькманн Г.М., Шуберт В. (2007) Геотехническая модель опор кровли труб при проходке туннелей. В: Бартак Дж., Хрдина И., Романцов Г., Зламал Дж. (Ред.) 33-й Всемирный туннельный конгресс ITA-AITES — подземное пространство — 4-е измерение мегаполисов. Taylor & Francis Group, Прага, стр. 755–760
Google ученый
Wykeham Farrance Engineering Limited (1968) Справочник по коробке постоянной скорости деформации и сдвига WF 2500.Wykeham Farrance Engineering Limited, Слау
Google ученый
% PDF-1.4
%
5558 0 объект
>
эндобдж
xref
5558 546
0000000016 00000 н.
0000015203 00000 п.
0000015393 00000 п. 0000015422 00000 н.
0000015474 00000 п.
0000015512 00000 п.
0000015674 00000 п.
0000015759 00000 п.
0000015844 00000 п.
0000015929 00000 п.
0000016013 00000 п.
0000016097 00000 п.
0000016181 00000 п.
0000016265 00000 п.
0000016349 00000 п.
0000016433 00000 п.
0000016517 00000 п.
0000016601 00000 п.
0000016685 00000 п.
0000016769 00000 п.
0000016853 00000 п.
0000016937 00000 п.
0000017021 00000 п.
0000017105 00000 п.
0000017189 00000 п.
0000017273 00000 п.
0000017357 00000 п.
0000017441 00000 п.
0000017525 00000 п.
0000017609 00000 п.
0000017693 00000 п.
0000017777 00000 п.
0000017861 00000 п.
0000017945 00000 п.
0000018029 00000 п.
0000018113 00000 п.
0000018197 00000 п.
0000018281 00000 п.
0000018365 00000 п.
0000018449 00000 п.
0000018533 00000 п.
0000018617 00000 п.
0000018701 00000 п.
0000018785 00000 п.
0000018869 00000 п.
0000018953 00000 п.
0000019037 00000 п.
0000019121 00000 п.
0000019205 00000 п.
0000019289 00000 п.
0000019373 00000 п.
0000015422 00000 н.
0000015474 00000 п.
0000015512 00000 п.
0000015674 00000 п.
0000015759 00000 п.
0000015844 00000 п.
0000015929 00000 п.
0000016013 00000 п.
0000016097 00000 п.
0000016181 00000 п.
0000016265 00000 п.
0000016349 00000 п.
0000016433 00000 п.
0000016517 00000 п.
0000016601 00000 п.
0000016685 00000 п.
0000016769 00000 п.
0000016853 00000 п.
0000016937 00000 п.
0000017021 00000 п.
0000017105 00000 п.
0000017189 00000 п.
0000017273 00000 п.
0000017357 00000 п.
0000017441 00000 п.
0000017525 00000 п.
0000017609 00000 п.
0000017693 00000 п.
0000017777 00000 п.
0000017861 00000 п.
0000017945 00000 п.
0000018029 00000 п.
0000018113 00000 п.
0000018197 00000 п.
0000018281 00000 п.
0000018365 00000 п.
0000018449 00000 п.
0000018533 00000 п.
0000018617 00000 п.
0000018701 00000 п.
0000018785 00000 п.
0000018869 00000 п.
0000018953 00000 п.
0000019037 00000 п.
0000019121 00000 п.
0000019205 00000 п.
0000019289 00000 п.
0000019373 00000 п. 0000019457 00000 п.
0000019541 00000 п.
0000019625 00000 п.
0000019709 00000 п.
0000019793 00000 п.
0000019877 00000 п.
0000019961 00000 п.
0000020045 00000 п.
0000020129 00000 н.
0000020213 00000 н.
0000020297 00000 п.
0000020381 00000 п.
0000020465 00000 п.
0000020549 00000 п.
0000020633 00000 п.
0000020717 00000 п.
0000020801 00000 п.
0000020885 00000 п.
0000020969 00000 п.
0000021053 00000 п.
0000021137 00000 п.
0000021221 00000 п.
0000021305 00000 п.
0000021389 00000 п.
0000021473 00000 п.
0000021557 00000 п.
0000021641 00000 п.
0000021725 00000 п.
0000021809 00000 п.
0000021893 00000 п.
0000021977 00000 п.
0000022061 00000 п.
0000022145 00000 п.
0000022229 00000 п.
0000022313 00000 п.
0000022397 00000 п.
0000022481 00000 п.
0000022565 00000 п.
0000022649 00000 п.
0000022733 00000 п.
0000022817 00000 п.
0000022901 00000 п.
0000022985 00000 п.
0000023069 00000 п.
0000023153 00000 п.
0000023237 00000 п.
0000023321 00000 п.
0000023405 00000 п.
0000019457 00000 п.
0000019541 00000 п.
0000019625 00000 п.
0000019709 00000 п.
0000019793 00000 п.
0000019877 00000 п.
0000019961 00000 п.
0000020045 00000 п.
0000020129 00000 н.
0000020213 00000 н.
0000020297 00000 п.
0000020381 00000 п.
0000020465 00000 п.
0000020549 00000 п.
0000020633 00000 п.
0000020717 00000 п.
0000020801 00000 п.
0000020885 00000 п.
0000020969 00000 п.
0000021053 00000 п.
0000021137 00000 п.
0000021221 00000 п.
0000021305 00000 п.
0000021389 00000 п.
0000021473 00000 п.
0000021557 00000 п.
0000021641 00000 п.
0000021725 00000 п.
0000021809 00000 п.
0000021893 00000 п.
0000021977 00000 п.
0000022061 00000 п.
0000022145 00000 п.
0000022229 00000 п.
0000022313 00000 п.
0000022397 00000 п.
0000022481 00000 п.
0000022565 00000 п.
0000022649 00000 п.
0000022733 00000 п.
0000022817 00000 п.
0000022901 00000 п.
0000022985 00000 п.
0000023069 00000 п.
0000023153 00000 п.
0000023237 00000 п.
0000023321 00000 п.
0000023405 00000 п. 0000023489 00000 п.
0000023573 00000 п.
0000023657 00000 п.
0000023741 00000 п.
0000023825 00000 п.
0000023909 00000 п.
0000023993 00000 п.
0000024077 00000 п.
0000024161 00000 п.
0000024245 00000 п.
0000024329 00000 п.
0000024413 00000 п.
0000024497 00000 п.
0000024581 00000 п.
0000024665 00000 п.
0000024749 00000 п.
0000024833 00000 п.
0000024917 00000 п.
0000025000 00000 н.
0000025083 00000 п.
0000025166 00000 п.
0000025249 00000 п.
0000025332 00000 п.
0000025415 00000 п.
0000025498 00000 п.
0000025581 00000 п.
0000025664 00000 п.
0000025747 00000 п.
0000025830 00000 н.
0000025913 00000 п.
0000025996 00000 н.
0000026079 00000 п.
0000026162 00000 п.
0000026245 00000 п.
0000026328 00000 п.
0000026411 00000 п.
0000026494 00000 п.
0000026577 00000 п.
0000026660 00000 п.
0000026743 00000 п.
0000026826 00000 н.
0000026909 00000 н.
0000026992 00000 п.
0000027075 00000 п.
0000027158 00000 п.
0000027241 00000 п.
0000027324 00000 п.
0000027407 00000 п.
0000023489 00000 п.
0000023573 00000 п.
0000023657 00000 п.
0000023741 00000 п.
0000023825 00000 п.
0000023909 00000 п.
0000023993 00000 п.
0000024077 00000 п.
0000024161 00000 п.
0000024245 00000 п.
0000024329 00000 п.
0000024413 00000 п.
0000024497 00000 п.
0000024581 00000 п.
0000024665 00000 п.
0000024749 00000 п.
0000024833 00000 п.
0000024917 00000 п.
0000025000 00000 н.
0000025083 00000 п.
0000025166 00000 п.
0000025249 00000 п.
0000025332 00000 п.
0000025415 00000 п.
0000025498 00000 п.
0000025581 00000 п.
0000025664 00000 п.
0000025747 00000 п.
0000025830 00000 н.
0000025913 00000 п.
0000025996 00000 н.
0000026079 00000 п.
0000026162 00000 п.
0000026245 00000 п.
0000026328 00000 п.
0000026411 00000 п.
0000026494 00000 п.
0000026577 00000 п.
0000026660 00000 п.
0000026743 00000 п.
0000026826 00000 н.
0000026909 00000 н.
0000026992 00000 п.
0000027075 00000 п.
0000027158 00000 п.
0000027241 00000 п.
0000027324 00000 п.
0000027407 00000 п. 0000027490 00000 н.
0000027573 00000 п.
0000027656 00000 н.
0000027739 00000 п.
0000027822 00000 н.
0000027905 00000 н.
0000027988 00000 н.
0000028071 00000 п.
0000028154 00000 п.
0000028237 00000 п.
0000028320 00000 п.
0000028403 00000 п.
0000028486 00000 п.
0000028569 00000 п.
0000028652 00000 п.
0000028735 00000 п.
0000028818 00000 п.
0000028901 00000 п.
0000028984 00000 п.
0000029067 00000 н.
0000029150 00000 п.
0000029233 00000 п.
0000029316 00000 п.
0000029399 00000 н.
0000029482 00000 н.
0000029565 00000 п.
0000029648 00000 н.
0000029731 00000 п.
0000029814 00000 п.
0000029897 00000 п.
0000029980 00000 н.
0000030063 00000 п.
0000030146 00000 п.
0000030229 00000 п.
0000030312 00000 п.
0000030395 00000 п.
0000030478 00000 п.
0000030561 00000 п.
0000030644 00000 п.
0000030726 00000 п.
0000030808 00000 п.
0000030889 00000 п.
0000030971 00000 п.
0000031156 00000 п.
0000031195 00000 п.
0000031299 00000 п.
0000033452 00000 п.
0000033710 00000 п.
0000027490 00000 н.
0000027573 00000 п.
0000027656 00000 н.
0000027739 00000 п.
0000027822 00000 н.
0000027905 00000 н.
0000027988 00000 н.
0000028071 00000 п.
0000028154 00000 п.
0000028237 00000 п.
0000028320 00000 п.
0000028403 00000 п.
0000028486 00000 п.
0000028569 00000 п.
0000028652 00000 п.
0000028735 00000 п.
0000028818 00000 п.
0000028901 00000 п.
0000028984 00000 п.
0000029067 00000 н.
0000029150 00000 п.
0000029233 00000 п.
0000029316 00000 п.
0000029399 00000 н.
0000029482 00000 н.
0000029565 00000 п.
0000029648 00000 н.
0000029731 00000 п.
0000029814 00000 п.
0000029897 00000 п.
0000029980 00000 н.
0000030063 00000 п.
0000030146 00000 п.
0000030229 00000 п.
0000030312 00000 п.
0000030395 00000 п.
0000030478 00000 п.
0000030561 00000 п.
0000030644 00000 п.
0000030726 00000 п.
0000030808 00000 п.
0000030889 00000 п.
0000030971 00000 п.
0000031156 00000 п.
0000031195 00000 п.
0000031299 00000 п.
0000033452 00000 п.
0000033710 00000 п. 0000034514 00000 п.
0000035130 00000 п.
0000035391 00000 п.
0000035646 00000 п.
0000038340 00000 п.
0000058522 00000 п.
0000073009 00000 п.
0000073083 00000 п.
0000073967 00000 п.
0000074192 00000 п.
0000074511 00000 п.
0000075007 00000 п.
0000075069 00000 п.
0000078965 00000 п.
0000079006 00000 п.
0000079068 00000 н.
0000079244 00000 п.
0000079357 00000 п.
0000079594 00000 п.
0000079811 00000 п.
0000080000 00000 н.
0000080162 00000 п.
0000080334 00000 п.
0000080486 00000 п.
0000080688 00000 п.
0000080936 00000 п.
0000081083 00000 п.
0000081226 00000 п.
0000081475 00000 п.
0000081598 00000 п.
0000081786 00000 п.
0000081933 00000 п.
0000082061 00000 п.
0000082249 00000 п.
0000082396 00000 п.
0000082557 00000 п.
0000082745 00000 п.
0000082892 00000 п.
0000083041 00000 п.
0000083223 00000 п.
0000083394 00000 п.
0000083576 00000 п.
0000083776 00000 п.
0000083923 00000 п.
0000084082 00000 п.
0000084266 00000 п.
0000084413 00000 п.
0000084584 00000 п.
0000034514 00000 п.
0000035130 00000 п.
0000035391 00000 п.
0000035646 00000 п.
0000038340 00000 п.
0000058522 00000 п.
0000073009 00000 п.
0000073083 00000 п.
0000073967 00000 п.
0000074192 00000 п.
0000074511 00000 п.
0000075007 00000 п.
0000075069 00000 п.
0000078965 00000 п.
0000079006 00000 п.
0000079068 00000 н.
0000079244 00000 п.
0000079357 00000 п.
0000079594 00000 п.
0000079811 00000 п.
0000080000 00000 н.
0000080162 00000 п.
0000080334 00000 п.
0000080486 00000 п.
0000080688 00000 п.
0000080936 00000 п.
0000081083 00000 п.
0000081226 00000 п.
0000081475 00000 п.
0000081598 00000 п.
0000081786 00000 п.
0000081933 00000 п.
0000082061 00000 п.
0000082249 00000 п.
0000082396 00000 п.
0000082557 00000 п.
0000082745 00000 п.
0000082892 00000 п.
0000083041 00000 п.
0000083223 00000 п.
0000083394 00000 п.
0000083576 00000 п.
0000083776 00000 п.
0000083923 00000 п.
0000084082 00000 п.
0000084266 00000 п.
0000084413 00000 п.
0000084584 00000 п. 0000084758 00000 п.
0000084855 00000 п.
0000085048 00000 п.
0000085157 00000 п.
0000085299 00000 п.
0000085403 00000 п.
0000085562 00000 п.
0000085676 00000 п.
0000085776 00000 п.
0000085933 00000 п.
0000086023 00000 п.
0000086175 00000 п.
0000086289 00000 п.
0000086405 00000 п.
0000086579 00000 п.
0000086723 00000 п.
0000086869 00000 п.
0000086993 00000 п.
0000087103 00000 п.
0000087207 00000 п.
0000087396 00000 п.
0000087500 00000 п.
0000087734 00000 п.
0000087955 00000 п.
0000088059 00000 п.
0000088313 00000 п.
0000088474 00000 п.
0000088564 00000 п.
0000088729 00000 п.
0000088833 00000 п.
0000089020 00000 н.
0000089110 00000 п.
0000089294 00000 п.
0000089448 00000 п.
0000089604 00000 п.
0000089772 00000 п.
0000089876 00000 п.
00000
0000084758 00000 п.
0000084855 00000 п.
0000085048 00000 п.
0000085157 00000 п.
0000085299 00000 п.
0000085403 00000 п.
0000085562 00000 п.
0000085676 00000 п.
0000085776 00000 п.
0000085933 00000 п.
0000086023 00000 п.
0000086175 00000 п.
0000086289 00000 п.
0000086405 00000 п.
0000086579 00000 п.
0000086723 00000 п.
0000086869 00000 п.
0000086993 00000 п.
0000087103 00000 п.
0000087207 00000 п.
0000087396 00000 п.
0000087500 00000 п.
0000087734 00000 п.
0000087955 00000 п.
0000088059 00000 п.
0000088313 00000 п.
0000088474 00000 п.
0000088564 00000 п.
0000088729 00000 п.
0000088833 00000 п.
0000089020 00000 н.
0000089110 00000 п.
0000089294 00000 п.
0000089448 00000 п.
0000089604 00000 п.
0000089772 00000 п.
0000089876 00000 п.
00000
00000 н. 00000
00000 п. 00000
00000 н.
0000090377 00000 п.
0000090563 00000 п.
0000090776 00000 п.
0000090908 00000 н.
0000091042 00000 п.
0000091211 00000 п.
0000091301 00000 п.
0000091500 00000 п. 0000091590 00000 н.
0000091777 00000 п.
0000091881 00000 п.
0000092005 00000 п.
0000092182 00000 п.
0000092310 00000 п.
0000092492 00000 п.
0000092663 00000 п.
0000092767 00000 н.
0000092879 00000 п.
0000093084 00000 п.
0000093174 00000 п.
0000093341 00000 п.
0000093431 00000 п.
0000093598 00000 п.
0000093688 00000 п.
0000093834 00000 п.
0000093972 00000 н.
0000094205 00000 п.
0000094395 00000 п.
0000094545 00000 п.
0000094635 00000 п.
0000094829 00000 н.
0000094947 00000 п.
0000095126 00000 п.
0000095232 00000 п.
0000095362 00000 п.
0000095569 00000 п.
0000095675 00000 п.
0000095819 00000 п.
0000096018 00000 п.
0000096124 00000 п.
0000096254 00000 п.
0000096475 00000 п.
0000096577 00000 п.
0000096755 00000 п.
0000096976 00000 п.
0000097078 00000 п.
0000097276 00000 н.
0000097489 00000 н.
0000097591 00000 п.
0000097719 00000 п.
0000097942 00000 п.
0000098044 00000 п.
0000098164 00000 п.
0000098385 00000 п.
0000098489 00000 н.
0000098685 00000 п.
0000091590 00000 н.
0000091777 00000 п.
0000091881 00000 п.
0000092005 00000 п.
0000092182 00000 п.
0000092310 00000 п.
0000092492 00000 п.
0000092663 00000 п.
0000092767 00000 н.
0000092879 00000 п.
0000093084 00000 п.
0000093174 00000 п.
0000093341 00000 п.
0000093431 00000 п.
0000093598 00000 п.
0000093688 00000 п.
0000093834 00000 п.
0000093972 00000 н.
0000094205 00000 п.
0000094395 00000 п.
0000094545 00000 п.
0000094635 00000 п.
0000094829 00000 н.
0000094947 00000 п.
0000095126 00000 п.
0000095232 00000 п.
0000095362 00000 п.
0000095569 00000 п.
0000095675 00000 п.
0000095819 00000 п.
0000096018 00000 п.
0000096124 00000 п.
0000096254 00000 п.
0000096475 00000 п.
0000096577 00000 п.
0000096755 00000 п.
0000096976 00000 п.
0000097078 00000 п.
0000097276 00000 н.
0000097489 00000 н.
0000097591 00000 п.
0000097719 00000 п.
0000097942 00000 п.
0000098044 00000 п.
0000098164 00000 п.
0000098385 00000 п.
0000098489 00000 н.
0000098685 00000 п. 0000098946 00000 п.
0000099046 00000 н.
0000099148 00000 н.
0000099365 00000 н.
0000099455 00000 п.
0000099714 00000 п.
0000099804 00000 п.
0000100099 00000 н.
0000100219 00000 п.
0000100347 00000 н.
0000100564 00000 н.
0000100654 00000 н.
0000100867 00000 н.
0000100971 00000 п.
0000101077 00000 н.
0000101322 00000 н.
0000101426 00000 н.
0000101558 00000 н.
0000101766 00000 н.
0000101924 00000 н.
0000102140 00000 н.
0000102276 00000 н.
0000102418 00000 н.
0000102600 00000 н.
0000102726 00000 н.
0000102848 00000 н.
0000102990 00000 н.
0000103180 00000 н.
0000103312 00000 н.
0000103454 00000 п.
0000103606 00000 н.
0000103762 00000 н.
0000103904 00000 н.
0000104044 00000 н.
0000104236 00000 п.
0000104448 00000 н.
0000104598 00000 п.
0000104826 00000 н.
0000105012 00000 н.
0000105168 00000 п.
0000105322 00000 н.
0000105480 00000 н.
0000105622 00000 н.
0000105756 00000 п.
0000105900 00000 н.
0000106044 00000 н.
0000106246 00000 п.
0000106428 00000 н.
0000098946 00000 п.
0000099046 00000 н.
0000099148 00000 н.
0000099365 00000 н.
0000099455 00000 п.
0000099714 00000 п.
0000099804 00000 п.
0000100099 00000 н.
0000100219 00000 п.
0000100347 00000 н.
0000100564 00000 н.
0000100654 00000 н.
0000100867 00000 н.
0000100971 00000 п.
0000101077 00000 н.
0000101322 00000 н.
0000101426 00000 н.
0000101558 00000 н.
0000101766 00000 н.
0000101924 00000 н.
0000102140 00000 н.
0000102276 00000 н.
0000102418 00000 н.
0000102600 00000 н.
0000102726 00000 н.
0000102848 00000 н.
0000102990 00000 н.
0000103180 00000 н.
0000103312 00000 н.
0000103454 00000 п.
0000103606 00000 н.
0000103762 00000 н.
0000103904 00000 н.
0000104044 00000 н.
0000104236 00000 п.
0000104448 00000 н.
0000104598 00000 п.
0000104826 00000 н.
0000105012 00000 н.
0000105168 00000 п.
0000105322 00000 н.
0000105480 00000 н.
0000105622 00000 н.
0000105756 00000 п.
0000105900 00000 н.
0000106044 00000 н.
0000106246 00000 п.
0000106428 00000 н. 0000106602 00000 п.
0000106810 00000 н.
0000106962 00000 н.
0000107114 00000 п.
0000107300 00000 н.
0000107458 00000 н.
0000107658 00000 н.
0000107800 00000 н.
0000107944 00000 н.
0000108062 00000 н.
0000108232 00000 н.
0000108432 00000 н.
0000108616 00000 п.
0000108800 00000 н.
0000108988 00000 н.
0000109120 00000 н.
0000109256 00000 н.
0000109362 00000 п.
0000109490 00000 н.
0000109711 00000 п.
0000109837 00000 п.
0000109967 00000 н.
0000110196 00000 н.
0000110342 00000 п.
0000110514 00000 п.
0000110703 00000 н.
0000110837 00000 н.
0000110953 00000 п.
0000111097 00000 н.
0000111272 00000 н.
0000111376 00000 н.
0000111550 00000 н.
0000111727 00000 н.
0000111817 00000 н.
0000111988 00000 н.
0000112126 00000 н.
0000112268 00000 н.
0000112423 00000 н.
0000112527 00000 н.
0000112653 00000 н.
0000112844 00000 н.
0000112964 00000 н.
0000113128 00000 н.
0000113298 00000 н.
0000113464 00000 н.
0000113616 00000 н.
0000113786 00000 н.
0000113946 00000 н.
0000106602 00000 п.
0000106810 00000 н.
0000106962 00000 н.
0000107114 00000 п.
0000107300 00000 н.
0000107458 00000 н.
0000107658 00000 н.
0000107800 00000 н.
0000107944 00000 н.
0000108062 00000 н.
0000108232 00000 н.
0000108432 00000 н.
0000108616 00000 п.
0000108800 00000 н.
0000108988 00000 н.
0000109120 00000 н.
0000109256 00000 н.
0000109362 00000 п.
0000109490 00000 н.
0000109711 00000 п.
0000109837 00000 п.
0000109967 00000 н.
0000110196 00000 н.
0000110342 00000 п.
0000110514 00000 п.
0000110703 00000 н.
0000110837 00000 н.
0000110953 00000 п.
0000111097 00000 н.
0000111272 00000 н.
0000111376 00000 н.
0000111550 00000 н.
0000111727 00000 н.
0000111817 00000 н.
0000111988 00000 н.
0000112126 00000 н.
0000112268 00000 н.
0000112423 00000 н.
0000112527 00000 н.
0000112653 00000 н.
0000112844 00000 н.
0000112964 00000 н.
0000113128 00000 н.
0000113298 00000 н.
0000113464 00000 н.
0000113616 00000 н.
0000113786 00000 н.
0000113946 00000 н. 0000114088 00000 н.
0000114224 00000 н.
0000114344 00000 п.
0000114502 00000 н.
0000114678 00000 н.
0000114802 00000 н.
0000114974 00000 н.
0000115168 00000 н.
0000115378 00000 п.
0000115512 00000 н.
0000115704 00000 н.
0000115892 00000 н.
0000116068 00000 н.
0000116206 00000 н.
0000116362 00000 н.
0000116506 00000 н.
0000116596 00000 н.
0000116700 00000 н.
0000116810 00000 н.
0000116987 00000 н.
0000117091 00000 н.
0000117201 00000 н.
0000117380 00000 н.
0000117484 00000 н.
0000117702 00000 н.
0000117873 00000 н.
0000118011 00000 н.
0000118195 00000 н.
0000118404 00000 н.
0000118508 00000 н.
0000118720 00000 н.
0000118891 00000 н.
0000118981 00000 п.
0000119109 00000 н.
0000119245 00000 н.
0000119383 00000 п.
0000119549 00000 н.
0000119681 00000 н.
0000119865 00000 н.
0000120081 00000 н.
0000120327 00000 н.
0000120559 00000 н.
0000120775 00000 н.
0000120983 00000 н.
0000121205 00000 н.
0000121373 00000 н.
0000121463 00000 н.
0000121644 00000 н.
0000114088 00000 н.
0000114224 00000 н.
0000114344 00000 п.
0000114502 00000 н.
0000114678 00000 н.
0000114802 00000 н.
0000114974 00000 н.
0000115168 00000 н.
0000115378 00000 п.
0000115512 00000 н.
0000115704 00000 н.
0000115892 00000 н.
0000116068 00000 н.
0000116206 00000 н.
0000116362 00000 н.
0000116506 00000 н.
0000116596 00000 н.
0000116700 00000 н.
0000116810 00000 н.
0000116987 00000 н.
0000117091 00000 н.
0000117201 00000 н.
0000117380 00000 н.
0000117484 00000 н.
0000117702 00000 н.
0000117873 00000 н.
0000118011 00000 н.
0000118195 00000 н.
0000118404 00000 н.
0000118508 00000 н.
0000118720 00000 н.
0000118891 00000 н.
0000118981 00000 п.
0000119109 00000 н.
0000119245 00000 н.
0000119383 00000 п.
0000119549 00000 н.
0000119681 00000 н.
0000119865 00000 н.
0000120081 00000 н.
0000120327 00000 н.
0000120559 00000 н.
0000120775 00000 н.
0000120983 00000 н.
0000121205 00000 н.
0000121373 00000 н.
0000121463 00000 н.
0000121644 00000 н.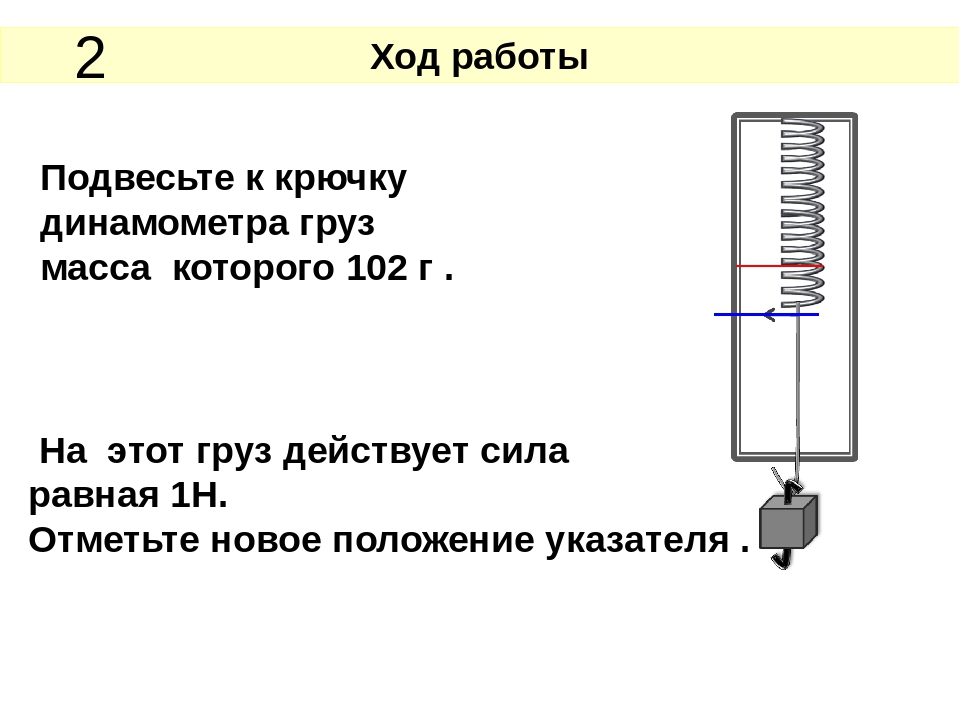 0000121734 00000 н.
0000121921 00000 н.
0000122041 00000 н.
0000122169 00000 н.
0000122376 00000 н.
0000122480 00000 н.
0000122646 00000 н.
0000122835 00000 н.
0000122939 00000 н.
0000123115 00000 н.
0000123322 00000 н.
0000123426 00000 н.
0000123616 00000 н.
0000123807 00000 н.
0000123921 00000 н.
0000124051 00000 н.
0000124270 00000 н.
0000124360 00000 н.
0000124561 00000 н.
0000124665 00000 н.
0000124825 00000 н.
0000125011 00000 н.
0000125165 00000 н.
0000125337 00000 н.
0000125503 00000 н.
0000125655 00000 н.
0000125825 00000 н.
0000125981 00000 п.
0000126135 00000 н.
0000126277 00000 н.
0000126457 00000 н.
0000126643 00000 н.
0000126817 00000 н.
0000127013 00000 н.
0000127193 00000 н.
0000127355 00000 н.
0000127507 00000 н.
0000127633 00000 н.
0000127809 00000 н.
0000127997 00000 н.
0000128139 00000 н.
0000128267 00000 н.
0000128353 00000 н.
0000128467 00000 н.
0000128589 00000 н.
0000128741 00000 н.
0000128831 00000 н.
0000129070 00000 н.
0000121734 00000 н.
0000121921 00000 н.
0000122041 00000 н.
0000122169 00000 н.
0000122376 00000 н.
0000122480 00000 н.
0000122646 00000 н.
0000122835 00000 н.
0000122939 00000 н.
0000123115 00000 н.
0000123322 00000 н.
0000123426 00000 н.
0000123616 00000 н.
0000123807 00000 н.
0000123921 00000 н.
0000124051 00000 н.
0000124270 00000 н.
0000124360 00000 н.
0000124561 00000 н.
0000124665 00000 н.
0000124825 00000 н.
0000125011 00000 н.
0000125165 00000 н.
0000125337 00000 н.
0000125503 00000 н.
0000125655 00000 н.
0000125825 00000 н.
0000125981 00000 п.
0000126135 00000 н.
0000126277 00000 н.
0000126457 00000 н.
0000126643 00000 н.
0000126817 00000 н.
0000127013 00000 н.
0000127193 00000 н.
0000127355 00000 н.
0000127507 00000 н.
0000127633 00000 н.
0000127809 00000 н.
0000127997 00000 н.
0000128139 00000 н.
0000128267 00000 н.
0000128353 00000 н.
0000128467 00000 н.
0000128589 00000 н.
0000128741 00000 н.
0000128831 00000 н.
0000129070 00000 н.


 (2 минуты)
(2 минуты)

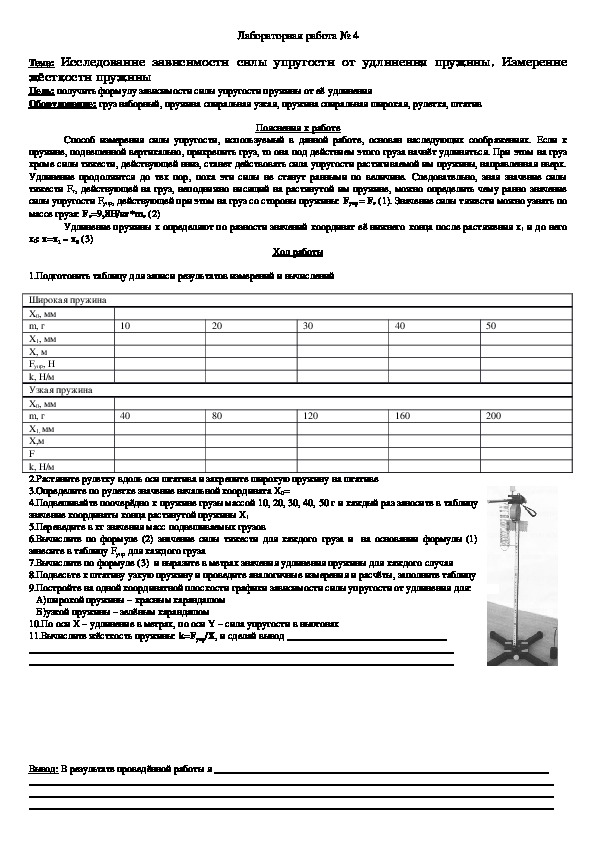

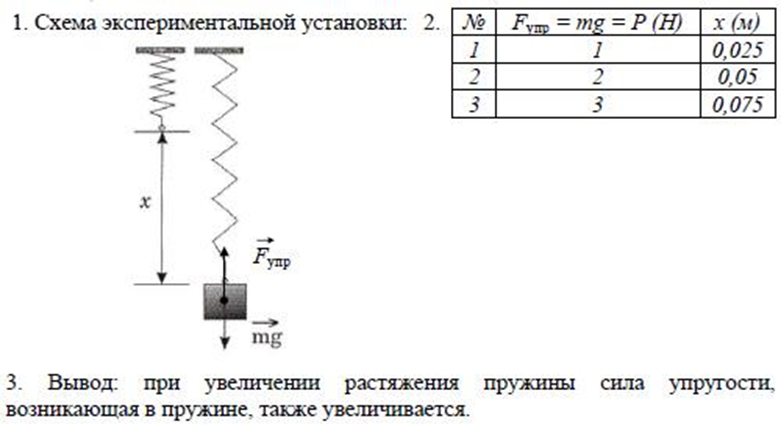



 ..
..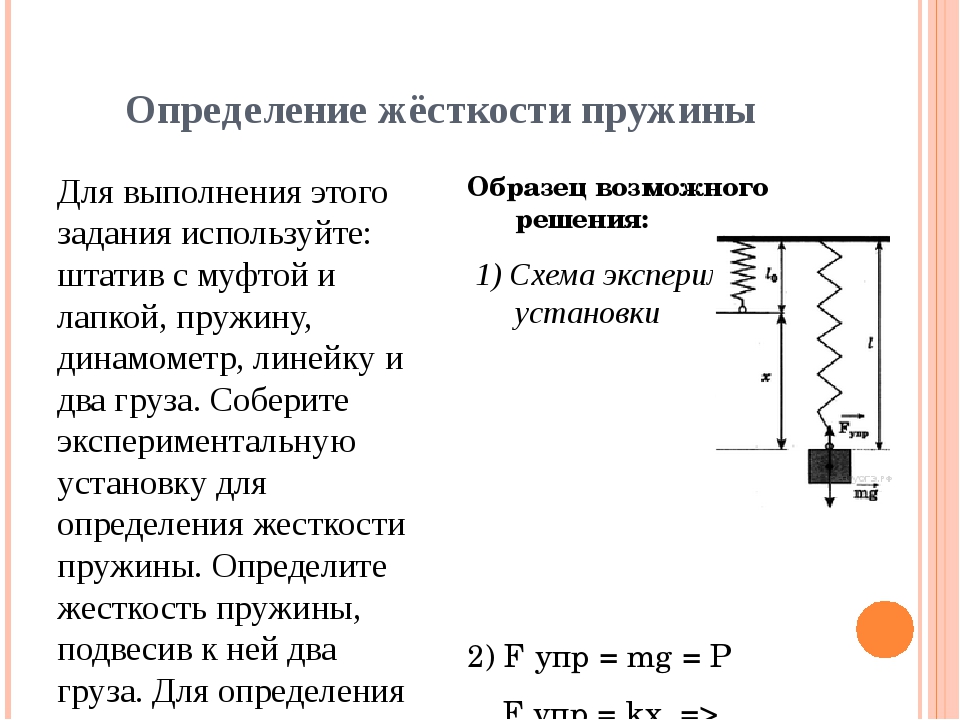
 1
1 Хотя точность лоренцевой аппроксимации тепловых спектров не отображается в программном обеспечении, необработанные и подогнанные кривые можно экспортировать, а среднеквадратическую ошибку можно вычислить вручную, чтобы найти положение, в котором шум является наименьшим, и, следовательно, отображаемую жесткость пружины. самый надежный.
Хотя точность лоренцевой аппроксимации тепловых спектров не отображается в программном обеспечении, необработанные и подогнанные кривые можно экспортировать, а среднеквадратическую ошибку можно вычислить вручную, чтобы найти положение, в котором шум является наименьшим, и, следовательно, отображаемую жесткость пружины. самый надежный.