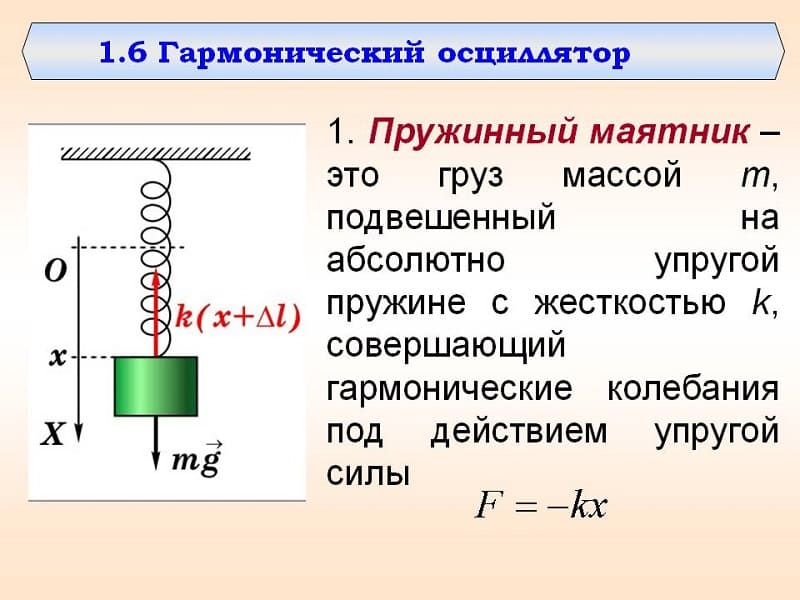
Лабораторная работа номер 2 измерение жесткости пружины. Измерение жесткости пружины
Урок 13/33
Тема. Лабораторная работа № 2 «Измерение жесткости пружины»
Цель урока: проверить справедливость закона Гука для пружины динамометра и измерить коэффициент жесткости этой пружины
Тип урока: контроля и оценивания знаний
Оборудование: штатив с муфтой и зажимом, динамометр с заклеенной шкалой, набор грузиков известной массы (по 100 г), линейка с миллиметровыми делениями
ХОД РАБОТЫ
1. Закрепите динамометр в штативе на достаточно большой высоте.
2. Подвешивая разное количество грузиков (от одного до четырех), вычислите для каждого случая соответствующее значение F = mg , а также измерьте соответствующее удлинение пружины х.
3. Результаты измерений и вычислений запишите в таблицу:
m , кг | mg, Н | ||
4. Начертите оси координат х и F
,
выберите удобный масштаб и нанесите полученные во время эксперимента точки.
Начертите оси координат х и F
,
выберите удобный масштаб и нанесите полученные во время эксперимента точки.
6. Вычислите коэффициент жесткости по формуле k = F /x , используя результаты опыта № 4 (это обеспечивает наибольшую точность).
7. Для вычисления погрешности следует использовать опыт, который мы получили во время поведення опыта № 4, потому что ему соответствует наименьшая относительная погрешность измерений. Вычислите пределы Fmin и Fmax , в которых находится истинное значение F , считая, что Fmin = F — ΔF , F = F + ΔF . Примите ΔF = 4Δm · g , где Δm — погрешность во время изготовления грузиков (для оценки можно считать, что Δm = 0,005 кг):
где Δх = 0,5 мм.
8. Пользуясь методом оценки погрешности косвенных измерений, вычислите:
9. Вычислите среднее значение kcep и абсолютную погрешность измерения Δk по формулам:
10. Вычислите относительную погрешность измерений:
11. Заполните таблицу:
Fmin, H | Fmax, H | xmin, м | xmax, м | kmin, Н/м | kmax, Н/м | k сэр, Н/м | ||
12. Запишите в тетради для лабораторных работ результат в виде k
= kcep
± Δk
, подставив в эту формулу числовые значения найденных величин.
Запишите в тетради для лабораторных работ результат в виде k
= kcep
± Δk
, подставив в эту формулу числовые значения найденных величин.
13. Запишите в тетради для лабораторных вывод: что вы измеряли и какой получили результат.
По
физике
за 9 класс (И.К.Кикоин, А.К.Кикоин, 1999 год),
задача
к главе «ЛАБОРАТОРНЫЕ РАБОТЫ ».
Цель работы: найти жесткость пружины из измерений удлинения пружины при различных значениях силы тяжести
уравновешивающей силу упругости на основе закона Гука:
В каждом из опытов жесткость определяется при разных значениях силы упругости и удлинения, т. е. условия опыта меняются. Поэтому для нахождения среднего значения жесткости нельзя вычислить среднее арифметическое результатов измерений. Воспользуемся графическим способом нахождения среднего значения, который может быть применен в таких случаях. По результатам нескольких опытов построим график зависимости модуля силы упругости F упр от модуля удлинения |x|. При построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле
При построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле
Это связано с погрешностями измерения. В этом случае график надо проводить так, чтобы примерно одинаковое число точек оказалось по разные стороны от прямой. После построения графика возьмите точку на прямой (в средней части графика), определите по нему соответствующие этой точке значения силы упругости и удлинения и вычислите жесткость k. Она и будет искомым средним значением жесткости пружины k ср.
Результат измерения обычно записывается в виде выражения k = = k cp ±Δk, где Δk — наибольшая абсолютная погрешность измерения. Из курса алгебры (VII класс) известно, что относительная погрешность (ε k) равна отношению абсолютной погрешности Δk к значению величины k:
откуда Δk — ε k k. Существует правило для расчета относительной погрешности: если определяемая в опыте величина находится в результате умножения и деления приближенных величин, входящих в расчетную формулу, то относительные погрешности складываются. В данной работе
В данной работе
Средства измерения: 1) набор грузов, масса каждого равна m 0 = 0,100 кг, а погрешность Δm 0 = 0,002 кг; 2) линейка с миллиметровыми делениями.
Материалы: 1) штатив с муфтами и лапкой; 2) спиральная пружина.
Порядок выполнения работы
1. Закрепите на штативе конец спиральной пружины (другой конец пружины снабжен стрелкой-указате-лем и крючком — рис. 176).
2. Рядом с пружиной или за ней установите и закрепите линейку с миллиметровыми делениями.
3. Отметьте и запишите то деление линейки, против которого приходится стрелка-указатель пружины.
4. Подвесьте к пружине груз известной массы и измерьте вызванное им удлинение пружины.
5. К первому грузу добавьте второй, третий и т. д. грузы, записывая каждый раз удлинение |х| пружины. По результатам измерений заполните таблицу:
6. По результатам измерений постройте график зависимости силы упругости от удлинения и, пользуясь им, определите среднее значение жесткости пружины k cp .
7. Рассчитайте наибольшую относительную погрешность, с которой найдено значение k ср (из опыта с одним грузом). В формуле (1)
так как погрешность при измерении удлинения Δx=1 мм, то
8. Найдите
и запишите ответ в виде:
1 Принять g≈10 м/с 2 .
Закон Гука: «Сила упругости, возникающая при деформации тела, пропорциональна его удлинению и направлена противоположно направлению перемещения частиц тела при деформации».
Закон Гука
Жесткостью называют коэффициент пропорциональности между силой упругости и изменением длины пружины под действием приложенной к ней силы. Согласно третьему закону Ньютона, приложенная к пружине сила по модулю равна возникшей в ней силе упругости. Таким образом жесткость пружины можно выразить как:
где F — приложенная к пружине сила, а х — изменение длины пружины под ее действием. Средства измерения: набор грузов, масса каждого равна m 0 = (0,1±0,002) кг.
Линейка с миллиметровыми делениями (Δх = ±0,5 мм). Порядок выполнения работы описан в учебнике и комментариев не требует.
Порядок выполнения работы описан в учебнике и комментариев не требует.
масса, кг | удлинение |х|, | |||
Решение задачи:
цель работы: найти жесткость пружины из измерений удлинения пружины при различных значениях силы тяжести
уравновешивающей силу упругости на основе закона гука:
в каждом из опытов жесткость определяется при разных значениях силы упругости и удлинения, т. е. условия опыта меняются. поэтому для нахождения среднего значения жесткости нельзя вычислить среднее арифметическое результатов измерений. воспользуемся графическим способом нахождения среднего значения, который может быть применен в таких случаях. по результатам нескольких опытов построим график зависимости модуля силы упругости f упр от модуля удлинения |x|. при построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле
это связано с погрешностями измерения.
 в этом случае график надо проводить так, чтобы примерно одинаковое число точек оказалось по разные стороны от прямой. после построения графика возьмите точку на прямой (в средней части графика), определите по нему соответствующие этой точке значения силы упругости и удлинения и вычислите жесткость k. она и будет искомым средним значением жесткости пружины k ср.
в этом случае график надо проводить так, чтобы примерно одинаковое число точек оказалось по разные стороны от прямой. после построения графика возьмите точку на прямой (в средней части графика), определите по нему соответствующие этой точке значения силы упругости и удлинения и вычислите жесткость k. она и будет искомым средним значением жесткости пружины k ср.результат измерения обычно записывается в виде выражения k = = k cp ±δk, где δk — наибольшая абсолютная погрешность измерения. из курса алгебры (vii класс) известно, что относительная погрешность (ε k) равна отношению абсолютной погрешности δk к значению величины k:
откуда δk — ε k k. существует правило для расчета относительной погрешности: если определяемая в опыте величина находится в результате умножения и деления приближенных величин, входящих в расчетную формулу, то относительные погрешности складываются. в данной работе
поэтому
средства измерения: 1) набор грузов, масса каждого равна m 0 = 0,100 кг, а погрешность δm 0 = 0,002 кг; 2) линейка с миллиметровыми делениями.
материалы: 1) штатив с муфтами и лапкой; 2) спиральная пружина.
порядок выполнения работы
1. закрепите на штативе конец спиральной пружины (другой конец пружины снабжен стрелкой-указате-лем и крючком — рис. 176).
2. рядом с пружиной или за ней установите и закрепите линейку с миллиметровыми делениями.
3. отметьте и запишите то деление линейки, против которого приходится стрелка-указатель пружины.
5. к первому грузу добавьте второй, третий и т. д. грузы, записывая каждый раз удлинение |х| пружины. по результатам измерений заполните таблицу:
номер опыта | m, кг | mg 1 , н | |х|, м |
6. по результатам измерений постройте график зависимости силы упругости от удлинения и, пользуясь им, определите среднее значение жесткости пружины k cp .
7. рассчитайте наибольшую относительную погрешность, с которой найдено значение k ср (из опыта с одним грузом). в формуле (1)
так как погрешность при измерении удлинения δx=1 мм, то
8. найдите
и запишите ответ в виде:
1 принять g≈10 м/с 2 .
закон гука: «сила упругости, возникающая при деформации тела, пропорциональна его удлинению и направлена противоположно направлению перемещения частиц тела при деформации».
закон гука
жесткостью называют коэффициент пропорциональности между силой упругости и изменением длины пружины под действием приложенной к ней силы. согласно третьему закону ньютона, приложенная к пружине сила по модулю равна возникшей в ней силе упругости. таким образом жесткость пружины можно выразить как:
где f — приложенная к пружине сила, а х — изменение длины пружины под ее действием. средства измерения: набор грузов, масса каждого равна m 0 = (0,1±0,002) кг.
линейка с миллиметровыми делениями (δх = ±0,5 мм). порядок выполнения работы описан в учебнике и комментариев не требует.
порядок выполнения работы описан в учебнике и комментариев не требует.
№ опыта | масса, кг | удлинение |х|, | к, н/м | |
м |
Разработка урока по физике по теме «Определение жесткости пружины»
Конспект урока по физике
Лабораторная работа
«Определение жесткости пружины» и
«Определение коэффициента трения скольжения»
Учебник «Физика 10 класс» авторы Л.Э. Генденштейн, Ю.И. Дик
Разработала:
Васильева Д.Н. учитель физики высшей квалификационной категории
Цель урока: в ходе проведения лабораторного практикума выработать общий подход к изучению сил электромагнитной природы, на примере силы трения и силы упругости.
Задачи урока:
Показать межпредметную связь физики и математики при обобщении результатов лабораторного исследования.

Отработка навыков работы с физическими приборами.
Вовлекать учащихся в активную творческую деятельность, воспитывать культуру общения на уроке и при изложении собственных мыслей.
Применяемые технологии: технология ИКТ
Применяемые формы работы: групповая работа в парах, работа с виртуальной лабораторией и реальным оборудованием.
На столах перед учениками: листочки с планом выполнения лабораторной работы, рисунком и расчётной таблицей, индивидуальным заданием, а так же — оборудование для определения жесткости пружины, ноутбук с установленной виртуальной лабораторной работой «Определение коэффициента трения скольжения»
На демонстрационном столе: деревянная линейка, деревянный брусок, набор грузиков, динамометр, штатив.
На доске: название лабораторных работ, координатные оси, для построения графиков при обсуждении результатов исследования, домашнее задание.
Ход урока:
Организационный момент.(1 минута)
Здравствуйте, ребята! Мне очень приятно видеть вас готовыми к уроку. Очень рассчитываю на нашу совместную плодотворную работу. Сегодня мы с вами продолжим исследование двух важнейших сил в природе — силы трения и силы упругости. Выступая в роли исследователей, попробуем определить, в чем сходство в этих на первый взгляд таких не похожих друг на друга силах и попытаемся в процессе исследования выработать общий подход к изучению подобных сил.
Фронтальный опрос.(5 минут)
| 1Когда возникает сила упругости? 2)Какие виды деформации вы знаете? 3)В чем заключается природа силы упругости? 4)От чего зависит величина силы упругости? 5)Что такое коэффициент упругости? |
Подготовка к выполнению работы.
 (2 минуты)
(2 минуты)
Провожу демонстрацию, перемещая брусок с грузом по поверхности деревянной линейки. Заостряю внимание на сложность равномерного перемещения двух трущихся поверхностей относительно друг друга и на колебания стрелки динамометра. Для исследования силы трения будем использовать виртуальную лабораторию (ноутбуки). Компьютер упрощает измерения. Нам лишь останется обработать результаты, полученные в виртуальном эксперименте. Также демонстрирую один из опытов второй лабораторной работы.
Одним из результатов исследования является определение коэффициента трения и коэффициента упругости по полученным в ходе работы зависимостям.
Для этого обращаю внимание ребят на распечатки, в которых описана лабораторная работа. Чтоб получить оценку «хорошо» — предстоит выполнить все задания из уровня «А» и если претендуете на более высокую оценку «отлично», то и уровень «В» также должен быть выполнен безошибочно. На каждую работу отводится 15 минут. В ходе урока ученики меняются местами с ребятами, выполняющими другое исследование. Таким образом, через 30 минут мы сможем подвести итоги работы.
В ходе урока ученики меняются местами с ребятами, выполняющими другое исследование. Таким образом, через 30 минут мы сможем подвести итоги работы.
Выполнение лабораторной работы.(30 минут)
В течение 15 минут учащиеся выполняют одну лабораторную работу. Из каждой группы учеников к доске вызывается 1 человек для построения полученной зависимости. И ученики, меняясь местами, заканчивают выполнение второй работы.
Анализ результатов выполненной работы.(5минут)
В конце урока на доске находятся 2 графика с помощью которых ученики определяли коэффициенты. Проговорим еще раз последовательность действий нахождения каждого из них. И обсудим следующие вопросы:
Как построить график по экспериментальным точкам?
Что такое аппроксимация?
Чему равен тангенс угла наклона графика? (При обсуждении этого вопроса на доске цветным мелом дорисовывается прямоугольный треугольник, из которого видно, что и .
 )
)Формулируем вывод о том, каков общий подход к изучению сил имеющих аналогичные зависимости.
В заключение урока(2 минуты).
Я благодарю вас за плодотворную работу! Мне хотелось бы узнать: с каким оборудованием вам было работать легче, интересней, результативней? Достигли ли мы поставленной цели?
Прошу записать Д/З: Тех, кто хотел бы повысить свою оценку может в домашней тетради провести расчет погрешностей экспериментов. Для всех остальных § 21 (Пункт1. Опр. наизусть)
Выходя из кабинета тетрадочки с лабораторными работами мне положить на край кафедры.
Спасибо за урок! До свиданья!
Приложения
Лабораторная работа №3
Определение жесткости пружины.
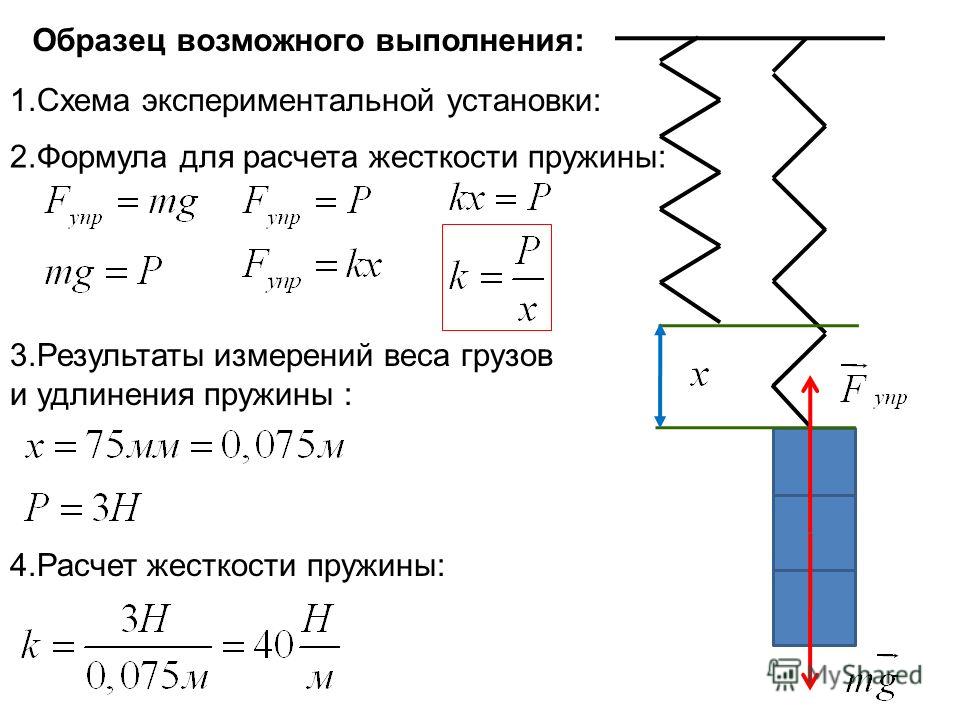
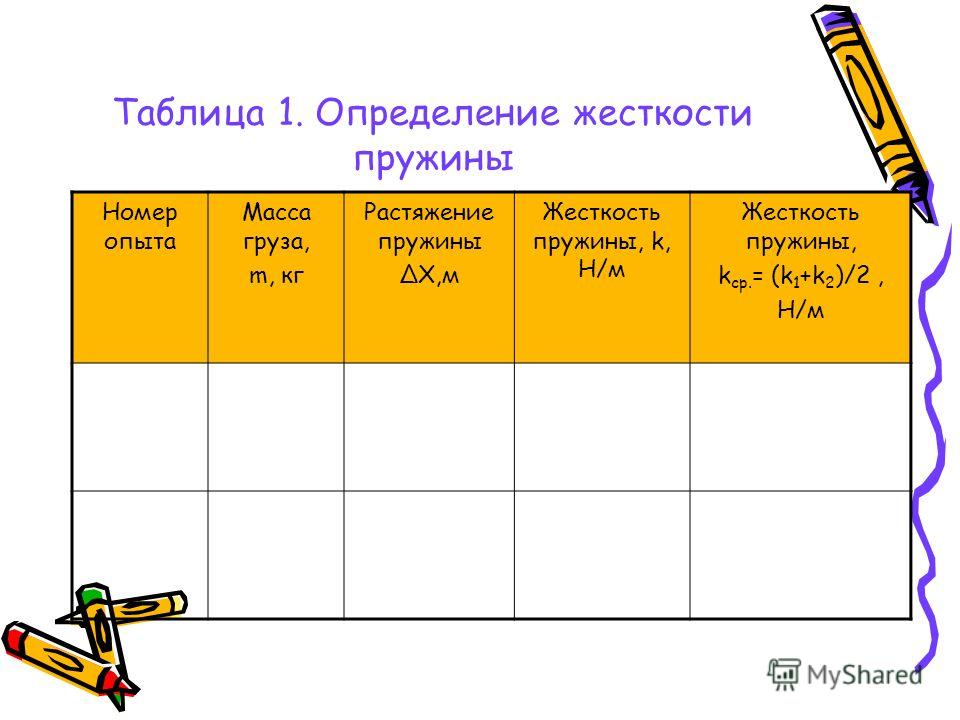
Цель работы: проверить справедливость закона Гука для пружины динамометра и измерить коэффициент жесткости этой пружины.
Оборудование: штатив с муфтой и зажимом, динамометр с заклеенной шкалой, набор грузов известной массы (по 100 г), линейка с миллиметровыми делениями.
Описание работы: Согласно закону Гука, модуль F силы упругости и модуль х. удлинения пружины связаны соотношением F=кх. Измерив F и х, можно найти коэффициент жесткости к по формуле к= F/х.
Ход работы:
Уровень «А»
Закрепите динамометр в штативе на достаточно большой высоте.
Подвешивая различное число грузов (от 1-го до 4-х), вычислите для каждого случая соответствующее значение F=mg, а также измерьте соответствующее удлинение пружины х.
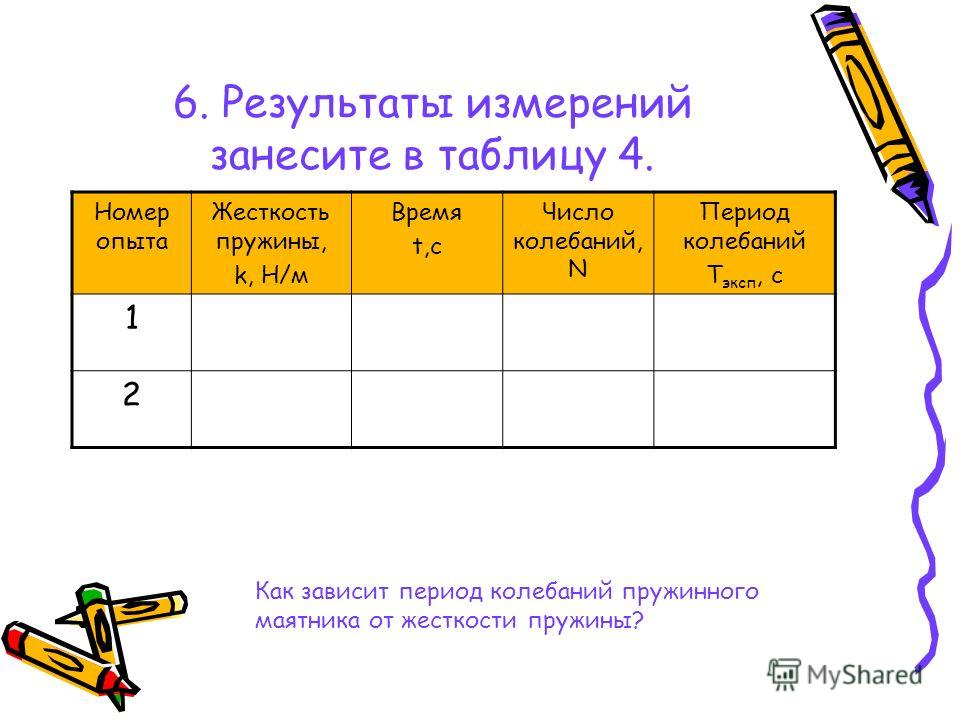
Результаты измерений и вычислений запишите в таблицу:
№ опыта
m, кг
mg, H
х, м
1
0,1
2
0,2
3
0,3
4
0,4
Начертите оси координат x и F, выберите удобный масштаб и нанесите полученные экспериментальные точки.

Оцените (качественно) справедливость закона Гука для данной пружины: находятся ли экспериментальные точки вблизи одной прямой, проходящей через начало координат.
Запишите сделанный вами вывод.
Вычислите коэффициент жесткости по формуле: k =F/х , используя результаты опыта №4 это обеспечит наибольшую точность.
Уровень «В»
8.Для вычисления погрешности надо использовать опыт №4, потому что ему соответствует наименьшая относительная погрешность измерения. Вычислите границы Fmin и Fmax , в которых находится истинное значение F , считая, что Fmin = F — ∆F, Fmax = F + ∆F. Примите ∆F = 4 ∆mg, где ∆m — погрешность при изготовлении грузов (для оценки можно считать, что ∆m= 0,005 кг).
xmin = x — ∆x, xmax = x + ∆x, где ∆x = 0,5мм,
Найденные величины запишите в приведенную ниже таблицу.
9.Пользуясь методом оценки погрешности косвенных измерений, найдите
kmax = Fmax/хmin , kmin = Fmin/хmax .
10. Найдите среднее значение kср и абсолютную погрешность измерения ∆ k по формулам
kср = (kmax + kmin) / 2, ∆k = (kmax — kmin)/2
11. Определите относительную погрешность измерения
Определите относительную погрешность измерения
Fmin, H | Fmax, H | xmin, м | xmax,м | kmin,Н/м | kmax,Н/м | kср,Н/м | ∆k,Н/м | ξk |
12. Запишите результат в виде k = kcр ± ∆к , подставив в эту формулу численные значения найденных величин:
13. Запишите вывод: что вы измеряли и какой получен результат.
Лабораторная работа №4
Определение коэффициента трения скольжения.
Цель работы: измерить коэффициент трения скольжения дерева по дереву.
Оборудование: деревянный брусок, деревянная линейка, набор грузов известной массы (по 100 г), динамометр.
Описание работы: Если тянуть брусок с грузом по горизонтальной поверхности так, чтобы брусок двигался равномерно, прикладываемая к бруску горизонтальная сила равна по модулю силе трения скольжения, действующей на брусок со стороны поверхности. Модуль силы трения Fтр связан модулем силы нормального давления N соотношением Fтр= μN . Измерив Fтр и N, можно найти коэффициент трения по формуле . В данном случае сила нормального давления N равна весу P бруска с грузом.
Ход работы:
Уровень «А»
Определите с помощью динамометра вес бруска Pбр и запишите в приведенную ниже таблицу.

Положите брусок на горизонтально расположенную деревянную линейку. На брусок поставьте груз.
Поставив на брусок один груз, тяните брусок равномерно по горизонтальной линейке, измеряя с помощью динамометра прикладываемую силу. Повторите опыт, поставив на брусок 2 и 3 груза. Записывайте каждый раз в таблицу значения силы трения Fтр и силы нормального давления N =Pбр+Ргр.
№ опыта
Pбр, H
N, H
Fтр ,Н
1
2
3
Начертите оси координат N и Fтр, выберите удобный масштаб и нанесите полученные три экспериментальные точки.

Оцените (качественно), подтверждается ли на опыте, что сила трения прямо пропорциональна силе нормального давления: находятся ли все экспериментальные точки вблизи одной прямой, проходящей через начало координат.
Запишите сделанный вами вывод.
Вычислите коэффициент трения по формуле , используя результаты опыта №3 (это обеспечивает наибольшую точность).
Уровень «В»
Для вычисления погрешности надо использовать опыт №3, потому что ему соответствует наименьшая относительная погрешность измерения. Вычислите границы Fmin и Fmax, в которых находится истинное значение F, считая, что Fmin=F-∆F, Fmax=F+∆F. С учетом того, что указатель динамометра при движении колеблется, можно принять ∆F=0,1Н.

Найдите границы Nmin и Nmax , в которых находится истинное значение N ,считая что N min =N — ∆N, Nmax= N + ∆N. Примите ∆N=3∆mg+∆Pбр, где ∆m – погрешность при изготовлении грузов (для оценки можно считать, что ∆m =0,005 кг, ∆Pбр=0,05H).
Пользуясь методом оценки погрешности косвенных измерений, найдите
,
Найдите среднее значение μср и абсолютную погрешность ∆μ по формулам:
,
Определите относительную погрешность измерения
Результаты вычислений запишите в таблицу:
Fmin, H
Fmax, H
Nmin, H
Nmax, H
μmin
μmax
μср
∆μ
ξμ
Запишите результат в виде μ = μср ± ∆μ, подставив в эту формулу численные значения найденных величин.

Запишите вывод: что вы измеряли и какой получен результат.
Что такое константа пружины и как рассчитывается формула?
4 июня 2018 г.
Пружины представляют собой упругие механические объекты, которые после деформации, т. е. после растяжения или сжатия, возвращаются к своей первоначальной форме. Они являются необходимым компонентом для самых разных механических устройств. От двигателей, приборов, инструментов, транспортных средств и медицинских инструментов до простых шариковых ручек знакомая металлическая катушка стала незаменимым компонентом в современном мире. Широкое использование и применение пружины обусловлено ее способностью накапливать механическую энергию. Его сила пружины является реактивной, которая генерирует механическую энергию. Сколько энергии представлено константой пружины.
Сила пружины — это сила, необходимая или прикладываемая для сжатия или растяжения пружины на любом объекте, прикрепленном к ней. Когда объект прикладывает силу к пружине, пружина прикладывает к объекту равную и противоположную силу. Он всегда действует так, чтобы возвращать массу обратно в положение равновесия. Постоянная пружины — это характеристика пружины, которая измеряет отношение силы, действующей на пружину, к вызванному ею смещению. Другими словами, он описывает, насколько жесткой является пружина и насколько она будет растягиваться или сжиматься. Пружины с большей жесткостью пружины будут иметь меньшие смещения, чем пружины с меньшей жесткостью пружины при той же добавленной массе.
Он всегда действует так, чтобы возвращать массу обратно в положение равновесия. Постоянная пружины — это характеристика пружины, которая измеряет отношение силы, действующей на пружину, к вызванному ею смещению. Другими словами, он описывает, насколько жесткой является пружина и насколько она будет растягиваться или сжиматься. Пружины с большей жесткостью пружины будут иметь меньшие смещения, чем пружины с меньшей жесткостью пружины при той же добавленной массе.
Определение силы пружины
Сила пружины рассчитывается с использованием закона Гука, названного в честь Роберта Гука, британского физика 17-го века, который разработал формулу в 1660 году, изучая пружины и упругость. Он заметил, что когда к материалу прикладывается сила, материал растягивается или сжимается в ответ на силу. Упругая деформация возникает при снятии напряжения. Это означает, что если материал возвращается к размерам, которые он имел до приложения нагрузки или напряжения, его деформация является обратимой, непостоянной, и он «пружинивает»9. 0003
0003
Формула усилия пружины выражается уравнением: F = – kx. Где F — приложенная сила, k — постоянная пружины, измеряющая, насколько жесткая и прочная пружина пропорционально, а x — расстояние, на которое пружина растягивается или сжимается от своего положения равновесия или покоя, обычно в ньютонах на метр (Н/м). ). Знак минус показывает, что эта сила имеет направление, противоположное силе, растягивающей или сжимающей пружину.
Постоянная пружины — это сила, необходимая для растяжения или сжатия пружины, деленная на расстояние, на которое пружина становится длиннее или короче. Он используется для определения стабильности или нестабильности пружины и, следовательно, системы, для которой он предназначен. В качестве формулы он перерабатывает закон Гука и выражается уравнением: k = – F/x. Где k — жесткость пружины, F — сила, приложенная к x, а x — смещение пружины, выраженное в Н/м.
Закон Гука описывает линейную упругую деформацию материалов только в том диапазоне, в котором сила и перемещение пропорциональны. Эластичность пружины вернется к своей первоначальной форме, как только внешняя сила, независимо от массы, будет устранена. Постоянная пружины — это свойство самой пружины, которое показывает линейную зависимость между силой и смещением. Таким образом, количество механической энергии, хранимой и используемой пружиной, зависит от силы и смещения: чем сильнее натягивается пружина, тем сильнее она тянет назад.
Эластичность пружины вернется к своей первоначальной форме, как только внешняя сила, независимо от массы, будет устранена. Постоянная пружины — это свойство самой пружины, которое показывает линейную зависимость между силой и смещением. Таким образом, количество механической энергии, хранимой и используемой пружиной, зависит от силы и смещения: чем сильнее натягивается пружина, тем сильнее она тянет назад.
Формула постоянной пружины — GeeksforGeeks
Простое гармоническое движение, или SHM, представляет собой увлекательный тип движения. Он обычно используется в колебательном движении объектов. SHM обычно встречается в источниках. Пружинам присущи «пружинные константы», которые определяют их жесткость. Закон Гука — хорошо известный закон, который объясняет SHM и дает формулу для приложенной силы с использованием жесткости пружины.
Закон Гука
Согласно закону Гука сила, необходимая для сжатия или растяжения пружины, пропорциональна растянутой длине. Когда пружина растягивается, третий закон движения Ньютона гласит, что она возвращается с возвращающей силой. Эта восстанавливающая сила подчиняется закону Гука, который связывает силу пружины с постоянной силой пружины.
Эта восстанавливающая сила подчиняется закону Гука, который связывает силу пружины с постоянной силой пружины.
Усилие пружины = -(Постоянная пружины) × (Перемещение)
F = -KX
Знак минус указывает, что сила реакции направлена в противоположном направлении.
Где,
F: Возвращающая сила пружины, направленная к равновесию.
K: жесткость пружины в Нм -1 .
X: Смещение пружины от положения равновесия.
Жесткость пружины (K)
Константа пружины теперь определяется как сила, необходимая на единицу растяжения пружины. Зная жесткость пружины, можно легко рассчитать, какое усилие требуется для деформации пружины.
Из закона Гука,
F = -KX
K = -F/ X ⇢ (1)
Уравнение (1) является формулой для жесткости пружины и измеряется в Н/м (ньютон на метр). .
Формула постоянных размеров пружины
Как известно,
F = -KX
Следовательно, K = -F/ X
Размерность F = [MLT -2 ]
Размерность X = [L]
Следовательно, размерность K = [MLT -2 ]/[L ] = [MT −2 ].
Потенциальная энергия пружины (PE)
Энергия, запасенная в сжимаемом или растягиваемом объекте, называется потенциальной энергией пружины. ее также называют упругой потенциальной энергией. Она равна произведению силы на пройденное расстояние.
Известно, что Потенциальная энергия = сила × смещение
А также сила пружины равна постоянной пружины × смещению. Итак,
Ч.Э. = 1/2 KX 2 .⇢ (2)
Приведенное выше уравнение представляет собой формулу потенциальной энергии пружины.
Ограничения закона Гука
Закон Гука имеет ограничение, заключающееся в том, что он применим только при пределе упругости любого материала, что означает, что материал должен быть абсолютно эластичным, чтобы подчиняться закону Гука. Закон Гука по существу нарушается за пределом эластичности.
Применение закона Гука
- Из-за эластичности пружин закон Гука чаще всего применяется весной.

- Они используются не только в области машиностроения, но и в области медицины.
- Он используется в легких, коже, пружинных матрасах, трамплинах и автомобильных подвесках.
- Это фундаментальный принцип, лежащий в основе манометра, пружинной шкалы и часового баланса.
- Он также является основой для сейсмологии, акустики и молекулярной механики.
Недостатки применения закона Гука
Ниже перечислены недостатки закона Гука:
- Закон Гука применим только в упругой области, после чего он не работает.
- Закон Гука дает точные результаты только для твердых тел с малыми силами и деформациями.
- Закон Гука не является общим правилом.
Примеры задач
Вопрос 1: Каково определение константы Spring?
Ответ:
При растяжении пружины прилагаемая сила пропорциональна увеличению длины от равновесной длины в соответствии с законом Гука.
Жесткость пружины можно рассчитать по следующей формуле: k = -F/x, где k — жесткость пружины. F обозначает силу, а x обозначает изменение длины пружины.
Вопрос 2: Как длина влияет на жесткость пружины?
Ответ:
Предположим, что имеется пружина 6 см с жесткостью k. Что произойдет, если пружину разделить на две равные части? Одна из этих более коротких пружин будет иметь новую жесткость 2k. В общем, при условии использования пружины из определенного материала и ее толщины жесткость пружины обратно пропорциональна длине пружины.
Итак, предположим, что в предыдущем примере пружину разрезали точно пополам, в результате чего получились две более короткие пружины, каждая по 3 см в длину. Для меньших пружин будет использоваться жесткость пружины, в два раза превышающая исходную. Это происходит потому, что она обратно пропорциональна как жесткости пружины, так и ее длине.
Вопрос 3: Пружина растягивается с силой 2 Н на 4 м.


 (2 минуты)
(2 минуты)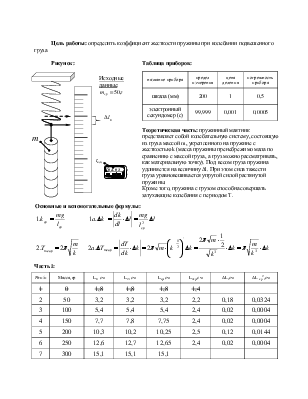 )
)



 Жесткость пружины можно рассчитать по следующей формуле: k = -F/x, где k — жесткость пружины. F обозначает силу, а x обозначает изменение длины пружины.
Жесткость пружины можно рассчитать по следующей формуле: k = -F/x, где k — жесткость пружины. F обозначает силу, а x обозначает изменение длины пружины.