ГДЗ (решебник) к учебнику Мерзляк А.Г. и др. Алгебра 10 класс (углубленный уровень) ФГОС ОНЛАЙН
Домашняя работа (решения, гдз, отвыты) по алгебре и началам анализа за 10 класс к учебнику авторов А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. «Алгебра и начала анализа 10 класс : учебник для учащихся общеобразовательных организаций (профильный уровень)».
В пособии решены и в большинстве случаев подробно разобраны задачи и упражнения из учебника «Мерзляк А.Г. Алгебра и начала математического анализа: 10 класс : учебник для учащихся общеобразовательных организаций ФГОС/ А.Г. Мерапяк, В.М. Поляков. — М., 2017. — 480 с. : ил. — (Российский учебник).».
Пособие адресовано родителям, которые смогут проконтролировать правильность решения, а в случае необходимости помочь детям в выполнении домашней работы по алгебре, а также учащимся для проверки правильности выполнения домашнего задания.
Купить учебник
Оглавление
Решебник готовится к публикации
Глава 1.
Повторение и расширение сведений о множествах, математической логике и функциях
§ 1. Множества. Операции над множествами
§ 2. Конечные и бесконечные множества
§ 3. Высказывания и операции над ними
§ 4. Предикаты. Операции над предикатами. Виды теорем
§ 5. Функция и её свойства
1 2 3 4 5 6 7 8 9 10 11 12§ 6. Построение графиков функций с помощью геометрических преобразований
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20§ 7. Обратная функция
1 2 3 4 5 6 7§ 8. Метод интервалов
1 2 3 4 5 6 7 8 9 10 Глава 2. Степенная функция
§ 9. Степенная функция с натуральным показателем
§ 10. Степенная функция с целым показателем
§ 11. Определение корня n-й степени. Функция
1 2 3 4 5 6 7 8 § 12.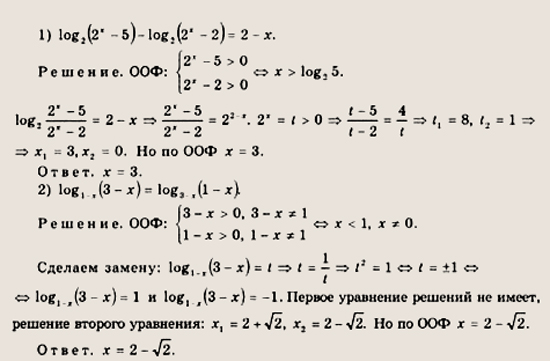
Свойства корня n-й степени
§ 13. Степень с рациональным показателем и её свойства
1 2 3 4 5 6 7 8§ 14. Иррациональные уравнения
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15§ 15. Различные приёмы решения иррациональных уравнений и их систем
1 2 3 4 5 6 7 8 9 10 11§ 16. Иррациональные неравенства
1 2 3 4 5 6 7 8 9 10 11Глава 3. Тригонометрические функции
§ 17. Радианная мера угла
§ 18. Тригонометрические функции числового аргумента
1 2 3 4 5§ 19. Знаки значений тригонометрических функций. Чётность и нечётность тригонометрических функций
§ 20. Периодические функции
1 2 3 4 5 6 7§ 21. Свойства и графики функций y=sin x и y=cos x
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 § 22.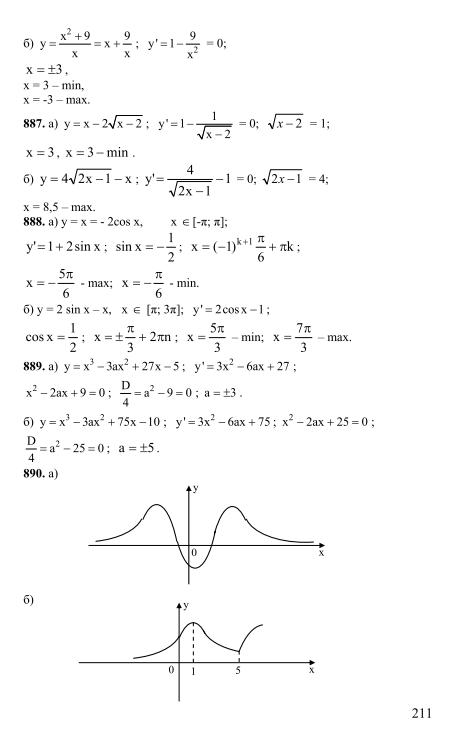
Свойства и графики функций y=tg x и y=ctg x
§ 23. Основные соотношения между тригонометрическими функциями одного и того же аргумента
1 2 3 4 5 6 7 8 9 10§ 24. Формулы сложения
1 2 3 4 5 6 7 8 9 10 11 12§ 25. Формулы приведения
1 2 3 4 5 6 7§ 26. Формулы двойного, тройного и половинного углов
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22§ 27. Формулы для преобразования суммы, разности и произведения тригонометрических функций
1 2 3 4 5 6 7 8 9 10 11 12 13 Глава 4. Тригонометрические уравнения и неравенства
§ 28. Уравнение cos x=b
§ 29. Уравнение sin x=b
1 2 3 4 5 6 7 8 9 10§ 30. Уравнения tg x=b и ctg x=b
1 2 3 4 § 31.
Функции y=arccos x, y=arcsin x, y=arctg x и y=arcctg x
§ 32. Тригонометрические уравнения, сводящиеся к алгебраическим
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25§ 33. Решение тригонометрических уравнений методом разложения на множители. Применение ограниченности тригонометрических функций
1 2 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23§ 34. О равносильных переходах при решении тригонометрических уравнений
1 2 3 4 5 6 7 8 9 10§ 35. Тригонометрические неравенства
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22Глава 5. Производная и её применение
§ 36. Определение предела функции в точке и функции, непрерывной в точке
§ 37. Задачи о мгновенной скорости и касательной к графику функции
§ 38.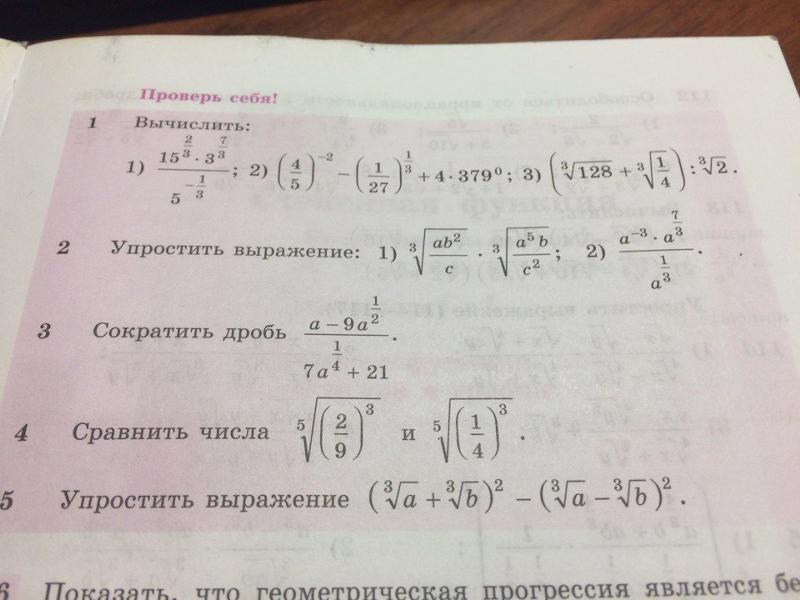
Понятие производной
§ 39. Правила вычисления производных
1 3 4 5 6 7 8 9 § 40. Уравнение касательной
§ 41. Признаки возрастания и убывания функции
§ 42. Точки экстремума функции
§ 43. Наибольшее и наименьшее значения функции на отрезке
§ 44. Вторая производная. Понятие выпуклости функции
§ 45. Построение графиков функций
Глава 6. Приложение. Элементы теории чисел. Метод математической индукции
§ 46. Делимость нацело и её свойства
§ 47. Деление с остатком. Сравнения по модулю и их свойства
§ 48. Наибольший общий делитель и наименьшее общее кратное двух натуральных чисел. Взаимно простые числа
§ 49. Простые и составные числа
• О проблемах, связанных с простыми числами
§ 50. Деление многочленов. Теорема Безу
§ 51. Целое рациональное уравнение
§ 52. Метод математической индукции
Упражнения для повторения курса алгебры и начал анализа 10 класса
Решебники (ГДЗ) для школьников | Математический помощник
ГДЗ, ответы, решения заданий, решебники к учебникам и сборникам заданий по математике для школьников в режиме онлайн
Избранное / Решебники (ГДЗ) для школьников
ГДЗ (решебник) к учебнику Мерзляк А.
Г. и др. Геометрия 11 класс (углубленный уровень) ФГОС ОНЛАЙНДомашняя работа (решения, гдз, отвыты) по геометрии за 10 класс к учебнику авторов А.Г. Мерзляк, Д.А. Номировский, В.М. Поляков. «Геометрия 11 класс : учебник для учащихся общеобразовательных организаций (углубленный уровень)». В пособии решены и в большинстве случаев подробно разобраны задачи и упражнения из учебника «Мерзляк А.Г., Номировский Д.А., Поляков В.М. …
Читать далее…
Избранное / Решебники (ГДЗ) для школьников
ГДЗ (решебник) к учебнику Мерзляк А.Г. и др. Геометрия 10 класс (углубленный уровень) ФГОС ОНЛАЙН
Домашняя работа (решения, гдз, отвыты) по геометрии за 10 класс к учебнику авторов А.Г. Мерзляк, Д.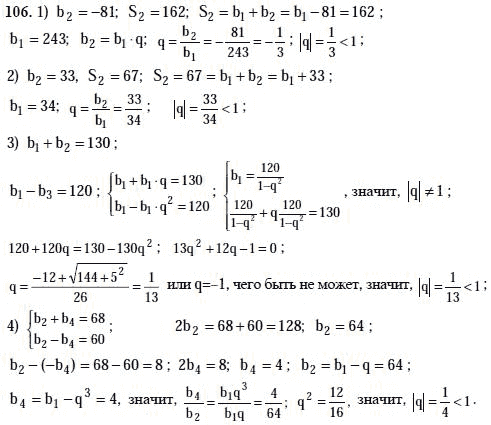
А. Номировский, В.М. Поляков. «Геометрия 10 класс : учебник для учащихся общеобразовательных организаций (углубленный уровень)». В пособии решены и в большинстве случаев подробно разобраны задачи и упражнения из учебника «Мерзляк А.Г., Номировский Д.А., Поляков В.М. …
Читать далее…
Избранное / Решебники (ГДЗ) для школьников
ГДЗ (решебник) к учебнику Мерзляк А.Г. и др. Геометрия 11 класс (базовый уровень) ФГОС ОНЛАЙН
Домашняя работа (решения, гдз, отвыты) по геометрии за 11 класс к учебнику авторов А.Г. Мерзляк, Д.А. Номировский, В.Б. Полонский, М.С. Якир. «Геометрия 10 класс : учебник для учащихся общеобразовательных организаций (базовый уровень)». В пособии решены и в большинстве случаев подробно разобраны задачи и упражнения из учебника «Мерзляк А.Г., Номировский Д.А., …
Читать далее.
..
Избранное / Решебники (ГДЗ) для школьников
ГДЗ (решебник) к учебнику Мерзляк А.Г. и др. Геометрия 10 класс (базовый уровень) ФГОС ОНЛАЙН
Домашняя работа (решения, гдз, отвыты) по геометрии за 10 класс к учебнику авторов А.Г. Мерзляк, Д.А. Номировский, В.Б. Полонский, М.С. Якир. «Геометрия 10 класс : учебник для учащихся общеобразовательных организаций (базовый уровень)». В пособии решены и в большинстве случаев подробно разобраны задачи и упражнения из учебника «Мерзляк А.Г., Номировский Д.А., …
Читать далее…
Избранное / Решебники (ГДЗ) для школьников
ГДЗ (решебник) к учебнику Мерзляк А.Г. и др. Алгебра 11 класс (углубленное изучение) ФГОС ОНЛАЙН
Домашняя работа (решения, гдз, отвыты) по алгебре и началам анализа за 11 класс к учебнику авторов А.
Г. Мерзляк, В.Б. Полонский, М.С. Якир. «Алгебра и начала математического анализа 11 класс : учебник для учащихся общеобразовательных организаций (профильный уровень)». В пособии решены и в большинстве случаев подробно разобраны задачи и упражнения из …
Читать далее…
Избранное / Решебники (ГДЗ) для школьников
ГДЗ (решебник) к учебнику Мерзляк А.Г. и др. Алгебра 11 класс (базовый уровень) ФГОС ОНЛАЙН
Домашняя работа (решения, гдз, отвыты) по алгебре и началам анализа за 11 класс к учебнику авторов А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. «Алгебра и начала анализа 11 класс : учебник для учащихся общеобразовательных организаций (базовый уровень)». В пособии решены и в большинстве случаев подробно разобраны задачи и упражнения из учебника …
Читать далее…
алгебраических уравнений |Определение| Типы| Решение алгебраических уравнений| Примеры
Алгебраическое уравнение можно определить как математическое выражение, в котором два выражения равны друг другу.
Алгебраическое уравнение обычно состоит из переменной, коэффициентов и констант.
Также проверьте: Алгебраические выражения.
Простыми словами, уравнения означают равенство, т.е. знак равенства. Вот что такое уравнения — «приравнивание одной величины к другой».
Алгебраические уравнения
Уравнения похожи на весы. Если вы видели весы, то должны знать, что на каждую сторону необходимо положить одинаковое количество веса, чтобы весы считались «сбалансированными». Если мы добавим вес только к одной стороне, весы наклонятся в одну сторону, и обе стороны больше не будут находиться в равновесии. Уравнения следуют той же логике. Все, что находится по одну сторону от знака равенства, должно иметь точно такое же значение по другую сторону, иначе оно станет неравенством.
Содержание:
|
Что такое алгебраические уравнения?
Алгебраическое уравнение — это уравнение в форме:
Р = 0
Где P — многочлен.
Например, x + 8 = 0 — алгебраическое уравнение, где x + 8 — многочлен. Поэтому его также называют полиномиальным уравнением.
Алгебраическое уравнение — это всегда сбалансированное уравнение, включающее переменные, коэффициенты и константы.
Рассмотрим уравнение 1+1 = 2.
Он сбалансирован, так как обе стороны имеют одинаковое значение. Чтобы избежать ошибки, которая выводит уравнение из равновесия, убедитесь, что любое изменение в одной части уравнения вызывает взаимное изменение в другой его части. Например, если вы хотите добавить число 5 к одной стороне уравнения, вам придется добавить те же 5 к другой стороне уравнения, то есть 9.0003
1 + 1 = 2
1 + 1 + 5 = 2 + 5
То же самое касается вычитания, умножения и деления. Пока вы делаете одно и то же с обеими частями уравнения, оно останется сбалансированным.
Что такое уравнение?
Уравнение определяется просто как математическое выражение, выражающее отношение между двумя значениями.
Обычно два значения приравниваются знаком равенства в уравнении.
Например, 2x+3 = 7 — это уравнение, где 2x+3 и 7 приравниваются знаком равенства «=».
2x+3 находится в левой части уравнения, а 7 — в правой. В этом примере
- 2x, 3 и 7 являются терминами
- x это переменная
- 3 и 7 — константы
- «+» — это оператор
Если мы пишем х = 3, то это тоже уравнение, где мы обозначаем значение переменной х равное 3.
Типы алгебраических уравнений
Алгебраические уравнения бывают разных типов. Вот несколько уравнений по алгебре:
- Полиномиальные уравнения
- Квадратные уравнения
- Кубические уравнения
- Рациональные полиномиальные уравнения
- Тригонометрические уравнения
Полиномиальные уравнения
Все полиномиальные уравнения являются частью алгебраических уравнений, как и линейные уравнения.
- Линейные уравнения: ax+b=c (a не равно 0)
Квадратные уравнения
Квадратное уравнение – это полиномиальное уравнение второй степени от одной переменной типа f(x) = ax 2 + bx + c.
- Квадратные уравнения: ax 2 +bx+c=0 (a не равно 0)
Кубические уравнения
Кубические многочлены — это многочлены степени 3. Все кубические многочлены также являются алгебраическими уравнениями.
- Кубические многочлены: ax 3 +bx 2 +сх+д=0
Рациональные полиномиальные уравнения
- Р(х)/Q(х)=0
Тригонометрические уравнения
Все тригонометрические уравнения считаются алгебраическими функциями. Для уравнения тригонометрии выражение включает тригонометрические функции переменной.
- Тригонометрические уравнения: cos2x = 1+4sinx
Как решать алгебраические уравнения
Рассмотрим следующую ситуацию. Я собираюсь в путешествие. В одной сумке ношу футболки, шорты и полотенца. Всего в сумке может поместиться 8 предметов. Итак, я упаковал 4 рубашки и 2 шорты. Сколько полотенец я теперь могу нести?
Считайте, что количество полотенец равно «x». Теперь составим уравнение.
4 рубашки + 2 шорты + полотенца «x» = 8 предметов одежды
Левая часть (LHS) нашего уравнения сравнивается с правой частью (RHS) уравнения.
Теперь давайте решим это уравнение:
4+2+х=8
6+х=8
6+x-6=8−6
х=2
Я могу взять с собой в поездку 2 полотенца.
Точно так же, что изобразит неравенство? Очевидно, когда левая часть не равна правой части. Как это произойдет?
Возьмем те же 6 + x = 8 и заменим знак равенства на знак больше или меньше. Это не уравнения! Рассмотрим несколько примеров, поясняющих это понятие.
x + 2 = 21, xy + 9 = z являются уравнениями, а 6p > 77 — нет.
Узнайте больше: Решение линейных уравнений
Решенные примеры
Q.1: Упростите данное уравнение: 2(x+4)+3(x–5)–2y=0
Решение:
Данное уравнение: 2(x+4)+3(x−5)–2y=0
2x+2×4+3x–3×5–2y=0 (Использование свойства Distribution для избавления от скобок)
2x+8+3x–15–2y=0 (упрощение)
5x–2y–7=0 (при дальнейшем упрощении)
Q.2: Решите x + 1 = 9
Решение: Дано, x+1 = 9
Если мы перенесем 1 из левой стороны в правую сторону, то изменится знак 1.
х = 9 – 1
х = 8
Значит, есть решение.
Q.3: Решите 15 + 5x = 0.
Решение: дано, 15 + 5x = 0,
Нам нужно найти x здесь.
Пусть член с x останется в левой части, а остальные члены переместятся в правую часть.
5x = 0 – 15
5x = -15
Теперь разделите обе стороны на 5.
(5x)/5 = -15/5
х = -3
Таким образом, x = -3 искомое решение.
Q.4: Решите -10x – 19 = 19 – 8x
Решение: Дано, -10x – 19 = 19 – 8x является алгебраическим уравнением.
Нам нужно решить данное уравнение относительно x.
Сначала запишите термины с x на одной стороне и другими терминами на другой стороне. Таким образом, мы добавим 8x к обеим сторонам
-10 х -19 + 8 х = 19 – 8 х + 8 х
Теперь сгруппируйте похожие термины.
-10x + 8x – 19 = 19
-2x – 19 = 19
Теперь добавьте 19 с обеих сторон.
-2x – 19 + 19 = 19 + 19
-2x = 38
Разделить обе части на 2
(-2x)/2 = 38/2
-х = 19
Умножить обе стороны на -1
-х (-1) = 19 (-1)
х = -19
Следовательно, x = -19 является требуемым решением.
Связанные статьи
Часто задаваемые вопросы – Часто задаваемые вопросы
Что такое алгебраические уравнения?
Алгебраическое уравнение — это математическое предложение, в котором два алгебраических выражения связаны знаком равенства (=).
Например, 3x+6 = 1 — это алгебраическое уравнение.
Что такое основы алгебры?
Основы алгебры включают математические операции, такие как сложение, вычитание, умножение и деление. Эти операции выполняются над уравнениями, состоящими из переменных и констант.
Является ли 10 алгебраическим выражением?
Нет, потому что алгебраическое выражение должно иметь переменную.
Как упростить алгебраические уравнения?
Для решения алгебраических уравнений выполните следующие шаги:
Удалите скобки () и умножьте множители
Объедините одинаковые члены и упростите их, добавив или вычитая
Объедините константы и упростите их, добавив или вычитая
Что такое основные правила алгебры?
Основные правила или законы алгебры:
Коммутативный закон ⇒ [x+y = y+x и x.y = y.x]
Ассоциативный закон ⇒ [x+(y+z) = (x+y)+z и x.(y.z) = (x.y).z]
Распределительный закон ⇒ [x.
(y+z) = x.y + x.z]
Алгебраические выражения (определение, основы, формулы и примеры решений)
Алгебраические выражения представляют собой выражение чисел с использованием букв или алфавитов без указания их фактических значений. Основы алгебры научили нас выражать неизвестное значение с помощью таких букв, как x, y, z и т. д. Эти буквы называются здесь переменными. Алгебраическое выражение может быть комбинацией как переменных, так и констант. Любое значение, которое помещается перед переменной и умножается на нее, является коэффициентом.
Что такое алгебраическое выражение?
Алгебраическое выражение в математике — это выражение, состоящее из переменных и констант, а также алгебраических операций (сложение, вычитание и т. д.). Выражения состоят из терминов. Кроме того, решайте вопросы в рабочих листах алгебраических выражений в BYJU’S.
Примеры
3x + 4y – 7, 4x – 10 и т. д.
Эти выражения представлены с помощью неизвестных переменных, констант и коэффициентов.
Комбинация этих трех (как терминов) называется выражением. Следует отметить, что, в отличие от алгебраического уравнения, алгебраическое выражение не имеет сторон или равно знаку. Некоторые из его примеров включают
- 3x + 2г – 5
- х – 20
- 2x 2 − 3xy + 5
Проверка: Математика 12 класс
Переменные, коэффициенты и константы в алгебраических выражениях
В алгебре мы работаем с переменными, символами или буквами, значение которых нам неизвестно.
В приведенном выше выражении (т.е. 5x – 3)
- x — это переменная , значение которой нам неизвестно и может принимать любое значение.
- 5 известен как c коэффициент x, поскольку это постоянное значение, используемое с переменным термином, и оно хорошо определено.
- 3 — это c постоянный термин значения, который имеет определенное значение.
Известно, что все выражение является биномиальным термином, поскольку оно имеет два маловероятных термина.
Типы алгебраических выражений
Существует 3 основных типа алгебраических выражений, в том числе:
- Мономиальное выражение
- Биномиальное выражение
- Полиномиальное выражение
Мономиальное выражение
Алгебраическое выражение, имеющее только один член, называется мономом.
Примеры одночленных выражений включают 3x 4 , 3xy, 3x, 8y и т. д.
Биномиальное выражение
Биномиальное выражение — это алгебраическое выражение, состоящее из двух непохожих членов.
Примеры бинома включают 5xy + 8, xyz + x 3 и т. д.
Полиномиальное выражение
В общем случае выражение, содержащее более одного члена с неотрицательными целыми показателями степени переменной, называется полиномом.
Примеры полиномиального выражения: ax + by + ca, x 3 + 2x + 3 и т. д.
Другие типы выражений
Помимо мономиальных, биномиальных и полиномиальных типов выражений, алгебраические выражения также можно разделить на два дополнительных типа:
- Числовое выражение
- Переменное выражение
Числовое выражение
Числовое выражение состоит из чисел и операций, но никогда не включает никаких переменных.
Некоторые примеры числовых выражений: 10 + 5, 15 ÷ 2 и т. д.
Переменное выражение
Переменное выражение — это выражение, которое содержит переменные вместе с числами и операцией для определения выражения. Несколько примеров выражения переменной: 4x + y, 5ab + 33 и т. д.
Алгебраическое выражение для класса 7
В 7 классе учащиеся встретятся с такими терминами алгебраических уравнений, как:
- Коэффициент члена
- Переменные
- Константа
- Коэффициенты срока
- Термины уравнений
- Термины «нравится» и «не нравится»
Ниже приведены примеры использования этих терминов.
If 2x 2 +3xy+4x+7 является алгебраическим выражением.
Тогда 2x 2 , 3xy, 4x и 7 являются терминами
Коэффициент срока x 2 = 2
Постоянный член = 7
Пример схожих и непохожих терминов:
Похожие термины: 2x и 3x
В отличие от терминов: 2x и 3y
Факторы срока:
Если 3xy — терм, то его делители равны 3, x и y.
Одночленный, биномиальный и трехчленный
Также в 7 классе мы узнаем о видах выражений, таких как одночлен, двучлен и трехчлен. Давайте посмотрим примеры каждого.
Одночлен: 2x
Бином: 2x+3y
Трехчлен: 2x+3y+9
Сложение и вычитание алгебраических выражений
Мы можем легко складывать и вычитать одинаковые члены.
Пример: сложите 3x + 5y – 6z и x – 4y + 2z.
Складывая оба выражения, мы получаем;
(3x + 5y – 6z) + (x – 4y + 2z)
Разделение похожих терминов и их сложение:
(3x + x) + (5y – 4y) + (-6z + 2z)
4x + у – 4z
Также читайте:
- Алгебраические тождества для класса 8
- Алгебраические тождества для класса 9
Формулы
Общие алгебраические формулы, которые мы используем для решения выражений или уравнений:
- (а + б) 2 = а 2 + 2аб + б 2
- (а – б) 2 = а 2 – 2аб + б 2
- а 2 – б 2 = (а – б)(а + б)
- (а + б) 3 = а 3 + б 3 + 3аб(а + б)
- (а – б) 3 = а 3 – б 3 – 3аб(а – б)
- а 3 – б 3 = (а – б)(а 2 + аб + б 2 )
- a 3 + b 3 = (a + b)(a 2 – ab + b 2 )
Решенная задача на алгебраическое выражение
Пример: Упростите данные выражения, комбинируя одинаковые термины, и запишите тип алгебраического выражения. (i) 3xy 3 + 9x 2 y 3 + 5y 3 x (ii) 7ab 2 c 2 + 2a 3 b 2 − 3abc – 5ab 2 c 2 – 2b 2 a 3 + 2ab (iii) 50x 3 – 20x + 8x + 21x 3 – 3x + 15x – 41x 3 Решение: Создание таблицы для поиска решения:
|
Часто задаваемые вопросы по алгебраическим выражениям
Как получить алгебраические выражения?
Алгебраическое выражение представляет собой комбинацию констант, переменных и алгебраических операций (+, -, ×, ÷).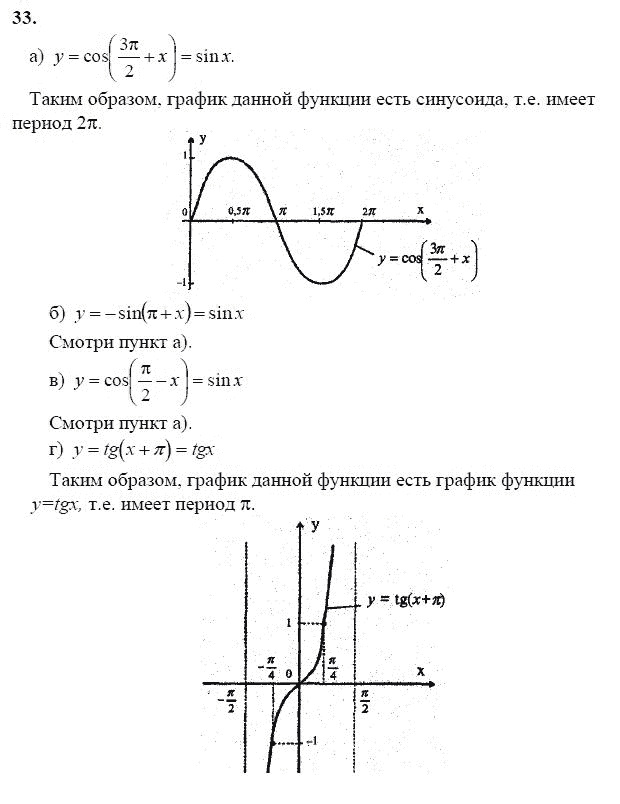
Мы можем вывести алгебраическое выражение для данной ситуации или условия, используя эти комбинации.
Например, возраст Симы в три раза больше, чем у Тины. А общий возраст Симы и Тины 40 лет. Выражая алгебраическую форму этого условия;
3x + x = 40 ⇒ 4x = 40; где x — возраст Тины.
Являются ли алгебраические выражения полиномами?
Нет, не все алгебраические выражения являются полиномами. Но все многочлены являются алгебраическими выражениями. Разница в том, что полиномы включают только переменные и коэффициенты с математическими операциями (+, -, ×), а алгебраические выражения также включают в себя иррациональные числа в степенях.
Кроме того, многочлены являются непрерывными функциями (например: x 2 + 2x + 1), но алгебраическое выражение иногда может быть не непрерывным (например: 1/x 2 – 1 не является непрерывным при 1).
Является ли 4 алгебраическим выражением?
Нет, 4 не является алгебраическим выражением, потому что выражение должно иметь хотя бы одну переменную и одну операцию, чтобы быть алгебраическим.