Алгебра мордкович 10 класс: Книга: «Математика. Алгебра. 10 класс. Учебник. Базовый и углубленный уровень. Комплект. В 2-х частях. ФГОС» — Мордкович, Денищева, Семенов. Купить книгу, читать рецензии | ISBN 978-5346-04514-4

Алгебра Мордкович 10 класс 1.9 — ГДЗ Решебники

Авторы: Мордкович, Александрова Год: 2013 год Издательство: Мнемозина

На данной странице предствлены решения к учебнику по Алгебре для учеников 10 класса, Учебник издательства «Мнемозина» 2013 года.

Популярные учебники

Числовые функции (Задания с 1.1 по 3.5)

§1. Определение числовой функции и способы ее задания

1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 1.10 1.11 1.12 1.13 1.14 1.15 1.16 1.17 1.18 1.19

§2. Свойства функций

2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.9 2.10 2.11 2.12 2.13 2.14 2.15

§3. Обратная функция

3.1 3.2 3.3 3.4 3.5

(Задания с 4.1 по 14.15) Тригонометрические функции

§4. Числовая окружность

4.1 4.2 4.3 4.4 4.5 4.6 4.7 4.8 4.9 4.10 4.11 4.12 4.13 4.14 4.15 4.16 4.17 4.18 4.19 4.20

§5. Числовая окружность на координатной плоскости

5.1 5.2 5.3 5.4 5.5 5. 6 5.7 5.8 5.9 5.10 5.11 5.12 5.13 5.14

§6. Синус и косинус. Тангенс и котангенс

6.1 6.2 6.3 6.4 6.5 6.6 6.7 6.8 6.9 6.10 6.11 6.12 6.13 6.14 6.15 6.16 6.18 6.19 6.20 6.21 6.22 6.23 6.24 6.25 6.26 6.27 6.28 6.29 6.30 6.31 6.32 6.33 6.34 6.35 6.36 6.37 6.38 6.39 6.40 6.41

§7. Тригонометрические функции числового аргумента

7.1 7.2 7.3 7.4 7.5 7.6 7.7 7.8 7.9 7.10 7.11 7.12 7.13 7.14 7.15 7.16 7.17 7.18 7.19 7.20

§8. Тригонометрические функции углового аргумента

8.1 8.2 8.3 8.4 8.5 8.6 8.7 8.8 8.9 8.10 8.11 8.12 8.13 8.14 8.15 8.16

§9. Формулы приведения

9.1 9.2 9.3 9.4 9.5 9.6 9.7 9.8 9.9 9.10 9.11 9.12 9.13 9.14

§10. Функция у = sin x, ее свойства и график

10.1 10.2 10.3 10.4 10.5 10.6 10.7 10.8 10.9 10.10 10.11 10.12 10.13 10.14 10.15 10.16 10.17 10.18

§11. Функция у = cos x, ее свойства и график

11.1 11.2 11.3 11.4 11.5 11.6 11.7 11.8 11.9 11.10 11.11 11.12 11.13

§12. Периодичность функций у = sin х, у = cos х

12.1 12.2 12. 3 12.4 12.5 12.6 12.7 12.8

§13. Преобразование графиков тригонометрических функций

13.1 13.2 13.3 13.4 13.5 13.6 13.7 13.8 13.9 13.10 13.11 13.12 13.13 13.14 13.15 13.16 13.17 13.18 13.19 13.20

§14. Функции у = tg х, у = ctg x, их свойства и графики

14.1 14.2 14.3 14.4 14.5 14.6 14.7 14.8 14.9 14.10 14.11 14.12 14.13 14.14 14.15

(Задания с 15.1 по 18.34) Тригонометрические уравнения

§15. Арккосинус. Решение уравнения cos t = a

15.1 15.2 15.3 15.4 15.5 15.6 15.7 15.8 15.9 15.10 15.11 15.12 15.13 15.14 15.15 15.16 15.17 15.18 15.19 15.20 15.21 15.22

§16. Арксинус. Решение уравнения sin t = a

16.1 16.2 16.3 16.4 16.5 16.6 16.7 16.8 16.9 16.10 16.11 16.12 16.13 16.14 16.15 16.16 16.17 16.18 16.19

§17. Арктангенс и арккотангенс. Решение уравнений tg х = a, ctg х = а

17.1 17.2 17.3 17.4 17.5 17.6 17.7 17.8 17.9 17.10

§18. Тригонометрические уравнения

18.1 18.2 18.3 18.4 18.5 18.6 18.7 18.8 18.9 18.10 18.11 18.12 18.13 18.14 18.15 18. 16 18.17 18.18 18.19 18.20 18.21 18.22 18.23 18.24 18.25 18.26 18.27 18.28 18.29 18.30 18.31 18.32 18.33 18.34

(Задания с 19.1 по 23.13) Преобразование тригонометрических выражений

§19. Синус и косинус суммы и разности аргументов

19.1 19.2 19.3 19.4 19.5 19.6 19.7 19.8 19.9 19.10 19.11 19.12 19.13 19.14 19.15 19.16 19.17 19.18 19.19 19.20 19.21 19.22 19.23 19.24 19.25 19.26

§20. Тангенс суммы и разности аргументов

20.1 20.2 20.3 20.4 20.5 20.6 20.7 20.8 20.9 20.10 20.11 20.12 20.13 20.14 20.15 20.16

§21. Формулы двойного аргумента

21.1 21.2 21.3 21.4 21.5 21.6 21.7 21.8 21.9 21.10 21.11 21.12 21.13 21.14 21.15 21.16 21.17 21.18 21.19 21.20 21.21 21.22 21.23 21.24 21.25 21.26 21.27 21.28 21.29 21.30 21.31 21.32 21.33 21.34 21.35 21.36 21.37 21.38

§22. Преобразование сумм тригонометрических функций в произведения

22.1 22.2 22.3 22.4 22.5 22.6 22.7 22.8 22.9 22.10 22.11 22.12 22.13 22.14 22.15 22.16 22.17 22.18 22.19 22.20 22.21 22.22

§23.

Преобразование произведений тригонометрических функций в суммы 23.1 23.2 23.3 23.4 23.5 23.6 23.7 23.8 23.9 23.10 23.11 23.12 23.13

Производная (Задания с 24.1 по 32.40)

§24. Предел последовательности

24.1 24.2 24.3 24.4 24.5 24.6 24.7 24.8 24.9 24.10 24.11 24.12 24.13 24.14 24.15 24.16 24.17 24.18 24.19 24.20 24.21 24.22

§25. Сумма бесконечной геометрической прогрессии

25.1 25.2 25.3 25.4 25.5 25.6 25.7 25.8 25.9 25.10 25.11 25.12 25.13 25.14 25.15

§26. Предел функции

26.1 26.2 26.3 26.4 26.5 26.6 26.7 26.8 26.9 26.10 26.11 26.12 26.13 26.14 26.15 26.16 26.17 26.18 26.19 26.20 26.21 26.22 26.23 26.24 26.25

§27. Определение производной

27.1 27.2 27.3 27.4 27.5 27.6 27.7 27.8 27.9 27.10 27.11 27.12 27.13 27.14

§28. Вычисление производных

28.1 28.2 28.3 28.4 28.5 28.6 28.7 28.8 28.9 28.10 28.11 28.12 28.13 28.14 28.15 28.16 28.17 28.18 28.19 28.20 28.21 28.22 28.23 28.24 28.25 28.26 28.27 28.28 28.29 28.30 28.31 28.32 28.33 28. 34 28.35 28.36 28.37 28.38 28.39 28.40 28.41 28.42 28.43 28.44 28.45 28.46

§29. Уравнение касательной к графику функции

29.1 29.2 29.3 29.4 29.5 29.6 29.7 29.8 29.9 29.10 29.11 29.12 29.13 29.14 29.15 29.16 29.17 29.18 29.19 29.20 29.21 29.22 29.23 29.24 29.25 29.26 29.27

§30. Применение производной для исследования функций на монотонность и экстремумы

30.1 30.2 30.3 30.4 30.5 30.6 30.7 30.8 30.9 30.10 30.11 30.12 30.13 30.14 30.15 30.16 30.17 30.18 30.19 30.20 30.21 30.22 30.23 30.24 30.25 30.26 30.27 30.28 30.29 30.30 30.31 30.32

§31. Построение графиков функций

31.1 31.2 31.3 31.4 31.5 31.6 31.7 31.8 31.9 31.10 31.11 31.12 31.13 31.14 31.15

§32. Применение производной для нахождения наибольших и наименьших значений величин

32.1 32.2 32.3 32.4 32.5 32.6 32.7 32.8 32.9 32.10 32.11 32.12 32.13 32.14 32.15 32.16 32.17 32.18 32.19 32.20 32.21 32.22 32.23 32.24 32.25 32.26 32.27 32.28 32.29 32.30 32.31 32.32 32.33 32.34 32.35 32.36 32.37 32.38 32.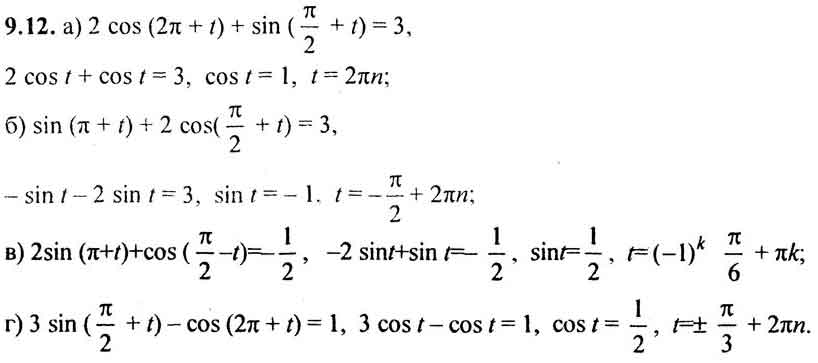 39 32.40

(Задания с 33.1 по 38.39) Степени и корни. Степенные функции

§33. Понятие корня n.й степени из действительного числа

33.1 33.2 33.3 33.4 33.5 33.6 33.7 33.8 33.9 33.10 33.11 33.12 33.13 33.14 33.15 33.16 33.17 33.18 33.19

§34. Функции у = n/х, их свойства и графики

34.1 34.2 34.3 34.4 34.5 34.6 34.7 34.8 34.9 34.10 34.11 34.12 34.13 34.14 34.15 34.16 34.17 34.18 34.19 34.20 34.21 34.22

§35. Свойства корня n.й степени

35.1 35.2 35.3 35.4 35.5 35.6 35.7 35.8 35.9 35.10 35.11 35.12 35.13 35.14 35.15 35.16 35.17 35.18 35.19 35.20 35.21 35.22 35.23 35.24 35.25 35.26 35.27 35.28 35.29 35.30

§36. Преобразование выражений, содержащих радикалы

36.1 36.2 36.3 36.4 36.5 36.6 36.7 36.8 36.9 36.10 36.11 36.12 36.13 36.14 36.15 36.16 36.17 36.18 36.19 36.20 36.21 36.22 36.23 36.24 36.25 36.26 36.27 36.28 36.29 36.30 36.31

§37. Обобщение понятия о показателе степени

37.1 37.2 37.3 37.4 37.5 37.6 37.7 37.8 37.9 37.10 37.11 37.12 37.13 37. 14 37.15 37.16 37.17 37.18 37.19 37.20 37.21 37.22 37.23 37.24 37.25 37.26 37.27 37.28 37.29 37.30 37.31 37.32 37.33

§38. Степенные функции, их свойства и графики

38.1 38.2 38.3 38.4 38.5 38.6 38.7 38.8 38.9 38.10 38.11 38.12 38.13 38.14 38.15 38.16 38.17 38.18 38.19 38.20 38.21 38.22 38.23 38.24 38.25 38.26 38.27 38.28 38.29 38.30 38.31 38.32 38.33 38.34 38.35 38.36 38.37 38.38 38.39

Показательная и логарифмическая функции (Задания с 39.1 по 47.28)

§39. Показательная функция, ее свойства и график

39.1 39.2 39.3 39.4 39.5 39.6 39.7 39.8 39.9 39.10 39.11 39.12 39.13 39.14 39.15 39.16 39.17 39.18 39.19 39.20 39.21 39.22 39.23 39.24 39.25 39.26 39.27 39.28 39.29 39.30 39.31 39.32 39.33 39.34 39.35 39.36 39.37 39.38 39.39 39.40 39.41 39.42

§40. Показательные уравнения и неравенства

40.1 40.2 40.3 40.4 40.5 40.6 40.7 40.8 40.9 40.10 40.11 40.12 40.13 40.14 40.15 40.16 40.17 40.18 40.19 40.20 40.21 40.22 40.23 40.24 40.25 40.26 40.27 40.28 40.29 40.30 40. 31 40.32 40.33 40.34 40.35 40.36 40.37 40.38 40.39 40.40 40.41 40.42 40.43 40.44 40.45 40.46 40.47 40.48 40.49 40.50

§41. Понятие логарифма

41.1 41.2 41.3 41.4 41.5 41.6 41.7 41.8 41.9 41.10 41.11 41.12 41.13 41.14 41.15 41.16 41.17 41.18 41.19

§42. Функция у = log a x, ее свойства и график

42.1 42.2 42.3 42.4 42.5 42.6 42.7 42.8 42.9 42.10 42.11 42.12 42.13 42.14 42.15 42.16 42.17 42.18 42.19 42.20 42.21 42.22 42.23 42.24 42.25

§43. Свойства логарифмов

43.1 43.2 43.3 43.4 43.5 43.6 43.7 43.8 43.9 43.10 43.11 43.12 43.13 43.14 43.15 43.16 43.17 43.18 43.19 43.20 43.21 43.22 43.23 43.24 43.25 43.26 43.27 43.28 43.29 43.30 43.31 43.32 43.33 43.34 43.35 43.36 43.37

§44. Логарифмические уравнения

44.1 44.2 44.3 44.4 44.5 44.6 44.7 44.8 44.9 44.10 44.11 44.12 44.13 44.14 44.15 44.16 44.17 44.18 44.19 44.20 44.21 44.22

§45. Логарифмические неравенства

45.1 45.2 45.3 45.4 45.5 45.6 45.7 45.8 45.9 45.10 45.11 45.12 45.13 45.14 45.15 45.16 45.17 45.

18

§46. Переход к новому основанию логарифма

46.1 46.2 46.3 46.4 46.5 46.6 46.7 46.8 46.9 46.10 46.11 46.12 46.13 46.14 46.15 46.16

§47. Дифференцирование показательной и логарифмической функций

47.1 47.2 47.3 47.4 47.5 47.6 47.7 47.8 47.9 47.10 47.11 47.12 47.13 47.14 47.15 47.16 47.17 47.18 47.19 47.20 47.21 47.22 47.23 47.24 47.25 47.26 47.27 47.28

Первообразная и интеграл (Задания с 48.1 по 49.34)

§48. Первообразная

48.1 48.2 48.3 48.4 48.5 48.6 48.7 48.8 48.9 48.10 48.11 48.12 48.13 48.14 48.15 48.16 48.17 48.18 48.19 48.20 48.21 48.22

§49. Определенный интеграл

49.1 49.2 49.3 49.4 49.5 49.6 49.7 49.8 49.9 49.10 49.11 49.12 49.13 49.14 49.15 49.16 49.17 49.18 49.19 49.20 49.21 49.22 49.23 49.24 49.25 49.26 49.27 49.28 49.29 49.30 49.31 49.32 49.33 49.34

Элементы математической статистики, комбинаторики и теории (Задания с 50.1 по 54.25)

§50. Статистическая обработка данных

50.1 50.2 50.3 50.4 50.5 50.6 50.7 50.8 50. 9 50.10 50.11

§51. Простейшие вероятностные задачи

51.1 51.2 51.3 51.4 51.5 51.6 51.7 51.8 51.9 51.10 51.11 51.12

§52. Сочетания и размещения

52.1 52.2 52.3 52.4 52.5 52.6 52.7 52.8 52.9 52.10 52.11 52.12 52.13 52.14 52.15 52.16 52.17 52.18 52.19 52.20

§53. Формула бинома Ньютона

53.1 53.2 53.3 53.4 53.5 53.6 53.7

§54. Случайные события и их вероятности

54.1 54.2 54.3 54.4 54.5 54.6 54.7 54.8 54.9 54.10 54.11 54.12 54.13 54.14 54.15 54.16 54.17 54.18 54.19 54.20 54.21 54.22 54.23 54.24 54.25

(Задания с 55.1 по 60.19) Уравнения и неравенства. Системы уравнений и неравенств

§55. Равносильность уравнений

55.1 55.2 55.3 55.4 55.5 55.6 55.7 55.8 55.9 55.10 55.11 55.12

§56. Общие методы решения уравнений

56.1 56.2 56.3 56.4 56.5 56.6 56.7 56.8 56.9 56.10 56.11 56.12 56.13 56.14 56.15 56.16 56.17 56.18 56.19 56.20 56.21 56.22 56.23 56.24 56.25 56.26 56.27 56.28 56.29 56.30 56.31 56.32 56.33 56.34 56.35 56.36 56.37 56.38 56.39 56. 40 56.41 56.42

§57. Решение неравенств с одной переменной

57.1 57.2 57.3 57.4 57.5 57.6 57.7 57.8 57.9 57.10 57.11 57.12 57.13 57.14 57.15 57.16 57.17 57.18 57.19 57.20 57.21 57.22 57.23 57.24 57.25 57.26 57.27 57.28 57.29 57.30 57.31 57.32 57.33

§58. Уравнения и неравенства с двумя переменными

58.1 58.2 58.3 58.4 58.5 58.6 58.7 58.8 58.9 58.10 58.11 58.12 58.13 58.14 58.15 58.16 58.17 58.18 58.19 58.20 58.21 58.22 58.23 58.24

§59. Системы уравнений

59.1 59.2 59.3 59.4 59.5 59.6 59.7 59.8 59.9 59.10 59.11 59.12 59.13 59.14 59.15 59.16 59.17 59.18 59.19 59.20 59.21 59.22 59.23 59.24 59.25 59.26 59.27

§60. Задачи с параметрами

60.1 60.2 60.3 60.4 60.5 60.6 60.7 60.8 60.9 60.10 60.11 60.12 60.13 60.14 60.15 60.16 60.17 60.18 60.19

БЕСПЛАТНОЕ ГДЗ ЗА 1-11 КЛАСС

Чтобы у учеников не было стресса от больших нагрузок, страха получить плохую оценку, но при этом оставалось время на полноценный сон, дополнительные занятия, спорт, общение со сверстниками, стоит делать уроки вместе с ГДЗ.

Готовые домашние задания – это возможность качественно подготовиться по разным предметам, не платя деньги репетиторам.

Если не хочется скачивать материалы, написанные «на коленке» студентами, а нужно работать с ГДЗ, над которыми трудились опытные преподаватели, умеющие понятно рассказывать теорию и грамотно оформлять практические задания, то надо заходить на Помогалку. Здесь можно без регистрации смотреть корректные решения номеров из учебников разных авторов по всем предметам и классам. Пусть школьная жизнь проходит без проблем!

Гдз мордкович 10 11 базовый

Что делать, если вы не разбираетесь в теме, а двойку так сильно не хотите? Просто списать решение с ГДЗ? Наверное, в 5-6 классе этот вариант казался многим ученикам самым идеальным решением проблемы. И родители довольны, и учитель ставит заслуженную тройку за работу.

Но что делать, если вы уже учитесь в аспирантуре и вам нужно подготовиться к взрослой жизни, выбрать профессию? Для успешной сдачи экзамена нужен хороший сертификат, а также база знаний. Всего этого не добиться без усилий.

Чтобы улучшить успеваемость по алгебре, можно нанять репетитора (не очень дешевый вариант) или попросить преподавателя (тоже нужно заплатить). Однако можно попробовать все сделать, максимально полагаясь на собственные усилия. Для этого вам понадобится ГДЗ по алгебре Мордковича 10-11 класс. Нет, не просто для списывания, а для эффективного самоконтроля за результатами обучения.

• При выполнении домашнего задания необходимо максимально опираться на изученный материал. Если у вас возникнут трудности, обратитесь за помощью к учителю.
• Используйте Решебник только для проверки выполненных заданий.
• Если вы нашли ошибку, то материал из руководства поможет вам разобраться, где она была допущена и в чем причина.
• Поддерживать базовые знания по материалам из готовых ответов.
• Обратитесь к учебнику и найдите правила, которые вы не использовали или использовали неправильно.

Здесь вы найдете все ответы по алгебре Мордковича 10-11 класс для онлайн

Хотим отметить, что на нашем сайте вы можете найти сборник решений Мордковича по алгебре 10-11 класс, а также многие другие методические пособия. Теперь вам достаточно зайти на наш сайт, и вы найдете то, что искали онлайн за пару минут. Авторизуйтесь со смартфонов и планшетов – получение информации для мобильных пользователей максимально доступно и удобно.

Все функции нашего сайта работают бесплатно. Не тратьте деньги на бумажные варианты ГДЗ — это уже прошлый век. Пришло время, когда информационные технологии дают новый толчок к приобретению полезных знаний, навыков и умений.

Теперь вы можете быть уверены, что сможете улучшить свои результаты по алгебре. Успешная сдача экзамена откроет вам дорогу в престижные учебные заведения, а это начало успешной карьеры.

6-е изд., Стер. – М.: 2009. – 424 с.

Учебник является первой частью комплекта из двух книг, предназначенного для изучения курса алгебры и начал математического анализа в 10 классе с профильной подготовкой по математике (вторая часть — задачник).

Формат: pdf

Размер: 5, 3 Mb

Смотреть, скачать:

Формат: djvu

6 9 Mb Размер

03

Смотреть, скачать: ссылок удалено (см. примечание!!)

СОДЕРЖАНИЕ
Предисловие учителя 3
Глава 1. Действительные числа
§ 1. Натуральные и целые числа 5
1. Делимость натуральных чисел 6
2. Признаки делимости 9
3. Простые и составные числа 14
4. Деление с остатком 15
5. Наибольший общий делитель и наименьшее общее кратное нескольких натуральных чисел 17
6. Основная теорема арифметики натуральных чисел 20
§ 2. Рациональные числа 22
§ 3. Иррациональные числа 27
§ 4. Множество действительных чисел 30
1. Вещественные числа и числовая прямая 30
2. Числовые неравенства 32
3. Числовые пробелы 39
4. Аксиоматика вещественные числа 40
§ 5. Модуль вещественного числа 43
§ 6. Метод математической индукции 45
Глава 2. Числовые функции
§ 7. Определение числовой функции и способы ее задания 55
§ 8. Свойства функций 67
§ 9. Периодические функции 80
§ 10. Обратная функция 82
Глава 3. Тригонометрические функции
§ 11. Числовой круг 86
§ 12. Числовой круг на координатной плоскости 97
§ 13. Синус и косинус. Тангенс и котангенс 104
1. Синус и косинус 104
2. Тангенс и котангенс 113
§ 14. Тригонометрические функции числового аргумента 117
§ 15. Тригонометрические функции углового аргумента 119
§ 16. Функции y = sin x, y = cos x, их свойства и графики 123
1. Функция y = sin x 123
2. Функция y = cos x 127
§ 17. Построение графика функции y = mf (x) 132
§ 18. Построение графика функции y = f (kx) 135
§ 19. График гармонических колебаний 139
§ 20. Функции y = tg x, y = ctg x, их свойства и графики 141
§ 21. Обратные тригонометрические функции 150
1. Функция y = arcsin x 150
2. Функция y = arccos x 157
3. Функция y = arctan x 160
4. Функция y = arcctg x 164
5. Преобразование выражений, содержащих обратные тригонометрические функции 166
Глава 4. Тригонометрические уравнения
§ 22. Простейшие тригонометрические уравнения и неравенства 170
1. Первые представления о простейших тригонометрических уравнениях 170
2. Решение уравнения cos t = a 172
3. Решение уравнения sin t = a 175
4. Решение уравнений tg x = a, ctg x = a 180
5. Простейшие тригонометрические уравнения 185
§ 23. Методы решения тригонометрических уравнений 189
1. Метод замены переменной 189
2. Метод факторизации 190
3. Однородные тригонометрические уравнения 191
Глава 5. Преобразование тригонометрических выражений
§ 24. Синус и косинус суммы и разности аргументов 198
§ 25. Тангенс сумма и разность аргументов 206
§ 26. Формулы приведения 209
§ 27. Формулы двойного аргумента.
Формулы убывания 214
Раздел 28. Преобразование сумм тригонометрическими функциями в работах 223
§ 29. Преобразование произведений тригонометрических функций в суммы 228
§ 30. Преобразование выражения A sin x + B cos x к виду C sin (* + t) 230
§ 31. Методы решения тригонометрических уравнений (продолжение ) 232
Глава 6. Комплексные числа
§ 32. Комплексные числа и арифметические действия над ними 240
§ 33. Комплексные числа и координатная плоскость 248
§ 34. Тригонометрическая запись комплексного числа 256
§ 35. Комплексные числа и квадратные уравнения 269
§ 36. Возведение комплексного числа в степень. Извлечение кубического корня комплексного числа. числовая последовательность 302
1. Определение предела последовательности 302
2. Свойства сходящихся последовательностей 307
3. Вычисление пределов последовательностей 308
4. Сумма бесконечной геометрической прогрессии 310
§ 39. Предел функции 312
1. Предел функции в бесконечности 312
2. Предел функции в точке 315
3. Приращение аргумента. Приращение функции 319
§ 40. Определение производной 322
1. Задачи, приводящие к понятию производной 322
2. Определение производной 325
§ 41. Вычисление производных 330
1. Формулы дифференцирования 330
2. Правила дифференцирования 334
3. Понятие и вычисление производной n-го порядка 340
§ 42. Дифференцирование комплексной функции. Дифференцирование обратной функции 341
§ 43. Уравнение касательной к графику функции 346
§ 44. Применение производной к изучению функций 352
1. Исследование функций на монотонность 352
2. Нахождение точек экстремума 356
3. Применение производной для доказательства тождеств и неравенств 362
§ 45. Построение графиков функций 363
§ 46. Применение производной для нахождения наибольшего и наименьшего значений величин 369
1. Нахождение наибольшего и наименьшего значения непрерывной функции на отрезке 369
2. Задачи на нахождение наибольшего и наименьшего значения величин 375
Глава 8. Комбинаторика и теория вероятностей
§ 47. Правило умножения. Перестановки и факториалы 381
§ 48. Выбор нескольких элементов.
Биномиальные коэффициенты 389
§ 49. Случайные события и их вероятности 403
Образец Тематическое планирование 417
Алфавитный указатель 420

Учебник является первой частью комплекта из двух книг, предназначенных для изучения курса алгебры и начал математического анализа в 10 класс со специальной подготовкой по математике (вторая часть — задачник).

Делимость натуральных чисел.
Определение 1. Пусть даны два натуральных числа — a и b. Если существует натуральное число q такое, что выполняется равенство a = bq, то говорят, что число a делится на число b. В этом случае число а называется делимым, b — делителем, q — частным. Число а также называют кратным числу b.

Из записи a = bq следует, что b является делителем a и что a кратно b. Однако из тех же обозначений следует, что q является делителем а и что а кратно q. Например, из записи 35 = 5·7 следует, что 35 делится на 5, а 35 делится на 7, что 35 кратно 5, а 35 кратно 7, что 5 является делителем 35 (и тогда 7 — частное) и что 7 — делитель 35 (и тогда 5 — частное).

СОДЕРЖАНИЕ
Предисловие для учителя. 3
Глава 1. Действительные числа
§ 1. Натуральные и целые числа. 5
1. Делимость натуральных чисел. 6
2. Критерии делимости. девять
3. Простые и составные числа. четырнадцать
4. Деление с остатком. 15
5. Наибольший общий делитель и наименьшее общее кратное нескольких натуральных чисел. 17
6. Основная теорема арифметики натуральных чисел. двадцать
§ 2. Рациональные числа. 22
§ 3. Иррациональные числа. 27
§ 4. Множество действительных чисел. тридцать
1. Действительные числа и числовой ряд. тридцать
2. Числовые неравенства. 32
3. Числовые интервалы. 39
4. Аксиоматика действительных чисел. 40
§ 5. Модуль вещественного числа. 43
§ 6. Метод математической индукции. 45
Глава 2. Числовые функции
§ 7. Определение числовой функции и способы ее задания. 55
§ 8. Свойства функций. 67
§ 9. Периодические функции. 80
§ 10. Обратная функция. 82
Глава 3. Тригонометрические функции
§ 11. Числовой круг. 86
§ 12. Числовая окружность на координатной плоскости. 97
§ 13. Синус и косинус. Тангенс и котангенс. 104
1. Синус и косинус. 104
2. Тангенс и котангенс. 113
§ 14. Тригонометрические функции числового аргумента. 117
§ 15. Тригонометрические функции углового аргумента. 119
§ 16. Функции y = sin xt y = cos x, их свойства и графики. 123
1. Функция y = sin x. 123
2. Функция y = cos x. 127
§ 17. Построение графика функции y = mf (x). 132
§ 18. Построение графика функции y = f (kx). 135
§ 19. График гармонических колебаний. 139
§ 20. Функции у = tg x, y — ctg x, их свойства и графики. 141
§ 21. Обратные тригонометрические функции. 150
1. Функция y = arcsin x. 150
2. Функция y = arccos x. 157
3. Функция y = arctan x. 160
4. Функция y = arcctg x. 164
5. Преобразование выражений, содержащих обратные тригонометрические функции. 166
Глава 4. Тригонометрические уравнения
§22. Простейшие тригонометрические уравнения и неравенства. 170
1. Первые представления о простейших тригонометрических уравнениях. 170
2. Решение уравнения cos t = a. 172
3. Решение уравнения sin t = a. 175
4. Решение уравнений tg x = a, ctg x = a. 180
5. Простейшие тригонометрические уравнения. 185
§ 23. Методы решения тригонометрических уравнений. 189
1. Метод замены переменной. 189
2. Метод факторизации. 190
3. Однородные тригонометрические уравнения. 191
Глава 5. Преобразование тригонометрических выражений
§ 24. Синус и косинус суммы и разности аргументов. 198
§ 25. Тангенс суммы и разности аргументов. 206
§ 26. Формулы приведения. 209
§ 27. Формулы двойного аргумента.
Формулы понижения степени. 214
§ 28. Преобразование сумм тригонометрических функций в произведения. 223
§ 29. Преобразование произведений тригонометрических функций в суммы. 228
§ 30. Преобразование выражения A sin x + B cos x к виду C sin (x + t). 230
§ 31. Методы решения тригонометрических уравнений (продолжение). 232
Глава 6. Комплексные числа
§ 32. Комплексные числа и арифметические действия над ними. 240
§ 33. Комплексные числа и координатная плоскость. 248
§ 34. Тригонометрическая форма записи комплексного числа. 256
§ 35. Комплексные числа и квадратные уравнения. 269 ​​
§ 36. Возведение комплексного числа в степень.
Извлечение кубического корня из комплексного числа. 280
Глава 7. Производная
§ 37. Числовые последовательности. 293
1. Определение числовой последовательности и способы ее присвоения. 293
2. Свойства числовых последовательностей. 298
§ 38. Предел числовой последовательности. 302
1. Определение предела последовательности. 302
2. Свойства сходящихся последовательностей. 307
3. Расчет пределов последовательностей. 308
4. Сумма бесконечной геометрической прогрессии. 310
§ 39. Предел функции. 312
1. Предел функции на бесконечности. 312
2. Предел функции в точке. 315
3. Увеличение аргумента. Инкремент функции. 319
§ 40. Определение производной. 322
1. Проблемы, ведущие к понятию производной. 322
2. Определение производной. 325
§ 41. Вычисление производных. 330
1. Формулы дифференцирования. 330
2. Правила дифференцирования. 334
3. Понятие и вычисление производной n-го порядка. 340
§ 42. Дифференцирование сложной функции.
Дифференцирование обратной функции. 341
§ 43. Уравнение касательной к графику функции. 346
§ 44. Применение производной для изучения функций. 352
1. Исследование функций на монотонность. 352
2. Нахождение точек экстремума. 356
3. Применение производной для доказательства тождеств и неравенств. 362
§ 45. Построение графиков функций. 363
§ 46. Применение производной для нахождения наибольшего и наименьшего значений величин. 369
1. Нахождение наибольшего и наименьшего значений непрерывной функции на отрезке. 369
2. Задачи на нахождение наибольшего и наименьшего значений величин. 375
Глава 8. Комбинаторика и вероятность
§ 47. Правило умножения. Перестановки и факториалы. 381
§ 48. Выбор нескольких элементов.
Биномиальные коэффициенты. 389
§ 49. Случайные события и их вероятности. 403
Примерная тематическая планировка. 417
Тематический указатель 420.

Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:
Скачать книгу Алгебра и начала математического анализа, 10 класс, Часть 1, Профильный уровень, Мордкович А.Г., Семенов П.В., 2009- fileskachat.com, быстрая и бесплатная загрузка.

Закажи решебник и скоро он будет на сайте

• 
  Облегчение поступления в ВУЗ. Вы можете дать ребенку конечную цель всего процесса обучения, тем самым убедив его в необходимости хорошей учебы. Родители часто говорят своим детям, что если они будут плохо учиться, то не смогут в будущем приобрести хорошую профессию и пойдут дворниками.
• 
  Школьное питание должно быть хорошо организовано. Студент должен быть обеспечен обедом и горячим завтраком в столовой. Интервал между первым и вторым приемом пищи не должен превышать четырех часов. Самый лучший вариант должен быть завтрак у ребенка дома, в школе он обедает
• 
  Установлена ​​определенная связь между детской агрессией и трудностями в обучении. Каждый ученик хочет иметь много друзей в школе, иметь хорошую успеваемость и хорошие оценки. Когда у ребенка это не получается, он совершает агрессивные действия. Каждое поведение направлено на что-то, имеет смысл
• 
  В любых олимпиадах и всевозможных конкурсах ребенок, прежде всего, самовыражается и реализуется. Родители обязательно должны поддерживать своего ребенка, если он увлечен интеллектуальным соревнованием. Ребенку важно осознать себя частью общества интеллектуалов, в котором царят соревновательные настроения, и ребенок сравнивает свои достижения
• 
  Проницательному ребенку может не понравиться школьная еда. Часто это самая распространенная причина, по которой ученик отказывается от еды. Все это происходит от того, что меню в школе не учитывает вкусовые потребности каждого отдельного ребенка. В школе никто не будет исключать из рациона отдельного ребенка какой-либо продукт, чтобы
• 
  Чтобы понять, как родители относятся к школе, важно сначала охарактеризовать современных родителей, возрастная категория которых очень разнообразна. Несмотря на это, большинство из них – родители, принадлежащие к поколению девяностых, отличающемуся непростым временем для всего населения.
• 
  Первые школьные сборы навсегда останутся в памяти каждого из нас. С августа родители начинают закупать все необходимые канцтовары. Главный школьный атрибут – школьная форма. Наряд должен быть тщательно подобран, чтобы первоклассник чувствовал себя уверенно. Введение школьной формы оправдано многими причинами.

Решение задач по алгебре и тригонометрии – Литвиненко Мордкович

Опубликовано 12 октября 2018 г. The Mitr

В этом посте мы увидим книгу Решение задач по алгебре и тригонометрии – В. Литвиненко, А. Мордкович. В предыдущем посте мы видели дополнительный том к этой книге Решение задач по геометрии . Сопутствующий том также был обновлен свежим сканированием и добавлены новые ссылки.

О книге:

Учебное пособие предназначено для студентов физико-математических факультетов педагогических институтов.
Книга содержит около 2000 примеров, задач и упражнений, из них 1700 задач для самостоятельного решения. Наряду с достаточно простыми задачами существуют и задачи, решение которых требует серьезной, а иногда и изобретательской работы. В ходе подготовки рукописи к печати мы постарались распределить место между основными типами «школьных» задач по алгебре и тригонометрии. Решение этих задач поможет студенту приобрести профессиональный навык, необходимый учителю, который должен уметь решать математические задачи школьного уровня.
Эта книга представляет собой не только сборник задач, это скорее учебное пособие для практической работы, что видно по структуре учебника. Каждый раздел содержит необходимый теоретический материал и большое количество отработанных примеров (общее количество которых составляет около 300), очень полезных для студента прежде всего с методической точки зрения.

Книга переведена с русского Леонидом Левантом и впервые опубликована издательством «Мир» в 1987 году.

PDF | В закладках | Обложка

Ссылка на Интернет-архив

Содержание

ЧАСТЬ 1. АЛГЕБРА 7

Глава 1. ИДЕНТИЧНЫЕ ПРЕОБРАЗОВАНИЯ 7

Разд. 1. Факторизация полиномов 7
сек. 2. Тождественные преобразования рациональных функций 11
сек. 3. Тождественные преобразования иррациональных функций 20
сек. 4. Тождественные преобразования показательных и логарифмических функций 29
сек. 5. Доказательство неравенств 33
Sec. 6. Сравнение числовых выражений 41

Глава 2.